苏科版九年级数学上册 2.1 圆教案

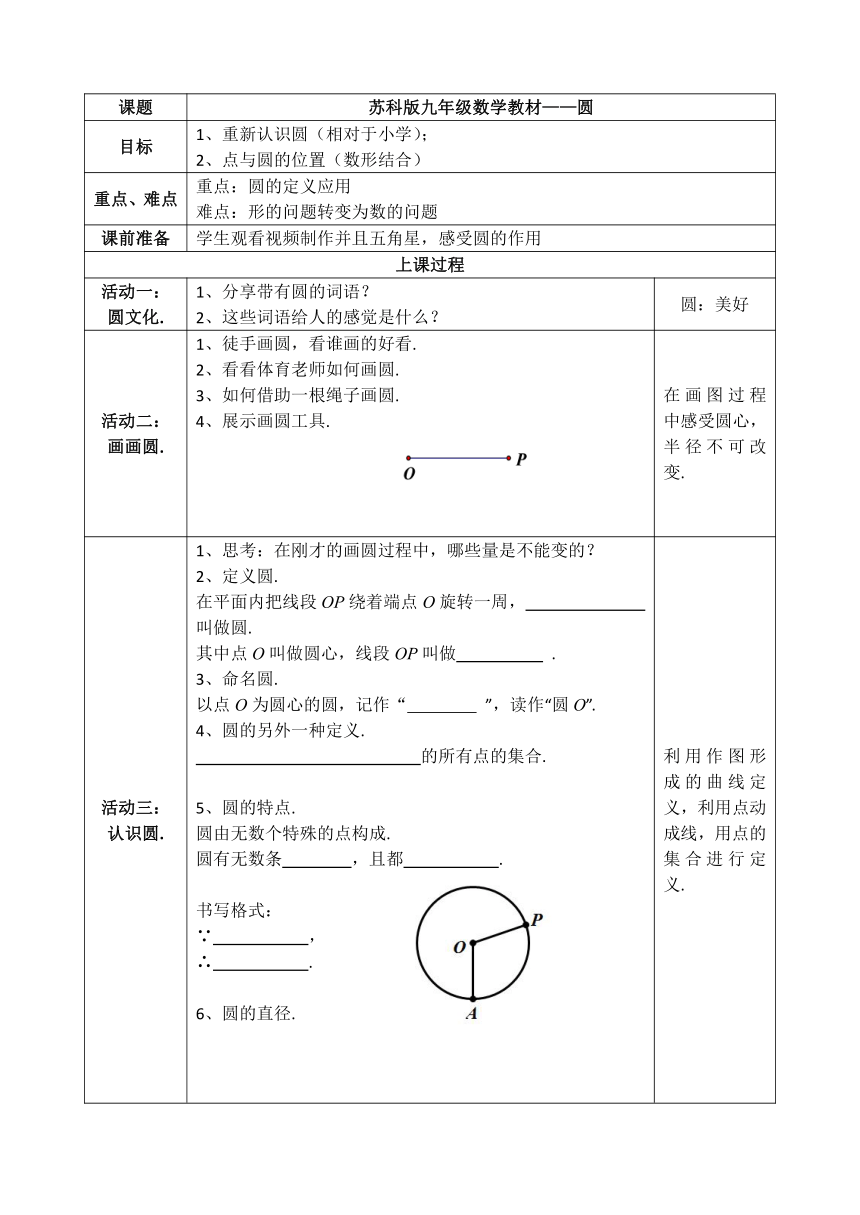
课题 苏科版九年级数学教材——圆
目标 1、重新认识圆（相对于小学）； 2、点与圆的位置（数形结合）
重点、难点 重点：圆的定义应用 难点：形的问题转变为数的问题
课前准备 学生观看视频制作并且五角星，感受圆的作用
上课过程
活动一： 圆文化. 1、分享带有圆的词语？ 2、这些词语给人的感觉是什么？ 圆：美好
活动二： 画画圆. 1、徒手画圆，看谁画的好看. 2、看看体育老师如何画圆. 3、如何借助一根绳子画圆. 4、展示画圆工具. 在画图过程中感受圆心，半径不可改变.
活动三： 认识圆. 1、思考：在刚才的画圆过程中，哪些量是不能变的？ 2、定义圆. 在平面内把线段OP绕着端点O旋转一周， 叫做圆. 其中点O叫做圆心，线段OP叫做 . 3、命名圆. 以点O为圆心的圆，记作“ ”，读作“圆O”. 4、圆的另外一种定义. 的所有点的集合. 5、圆的特点. 圆由无数个特殊的点构成. 圆有无数条 ，且都 . 书写格式： ∵ ， ∴ . 6、圆的直径. 利用作图形成的曲线定义，利用点动成线，用点的集合进行定义.
活动四： 点与圆. 1、回忆圆的定义：无数个特殊点构成. 2、平面内有无数个点，这些点与圆的位置可以分为几类？
3、如图，直角△ABC中，∠ACB=90°，CD⊥AB于D点，且AC=4，BC=3. （1）若以C点为圆心，CB为半径作圆， 求点D与⊙C的位置关系. （2）若以C点为圆心，r为半径作圆， 且点A,D,B三点中， 只有一个点在圆内， 另两个点在圆外， 求r的范围. 4、思考：矩形的四个顶点在同一个圆上吗？ 菱形呢、正方形、平行四边形呢？ 圆由无数的有规律的点构成，平面内的点进行分类，从而得到不同的位置关系.由于不同类别的点到圆心距离不一样，使学生学会用数的比较来区分不同的位置.渗透数形结合思想.
活动五： 练习圆. 1、如图，点A，B在⊙O上，∠O=120°，则∠A= °. 2、如图，点A，B在⊙O上，D为AB中点，求证：OD⊥AB. 3、如图，AB是⊙O直径，点D，E在⊙O上，延长BA、ED交于点C，且CD=OA，∠C=20°，求∠EOB. 注意辅助线半径的使用，再次感受圆上的点的特征.
活动六： 利用圆. 1、为什么车轮是圆的？ 2、为什么窨井盖大多是圆的？ 3、展示五角星. 感受生活中圆的用处
活动七： 小结圆. 1、圆的定义； 2、圆的性质； 3、点与圆的位置关系.