苏科版九年级数学上册 1.1 一元二次方程(课件)(共17张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 1.1 一元二次方程(课件)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 167.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
1.1 一元二次方程
问题2:学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册,平均每年增长的增长率是多少?
问题1:正方形桌面的面积是2m2,设正方形的边长是x m,求它的边长。
x2=2
5(1+x)2=7.2
自学反馈:
问题3:如图, 矩形花圃一面靠墙,另外三面所围的栅栏的总长度是19米,如果花圃的面积是24平方米,求花圃的长与宽。
墙
x
19-2x
x(19-2x)=24
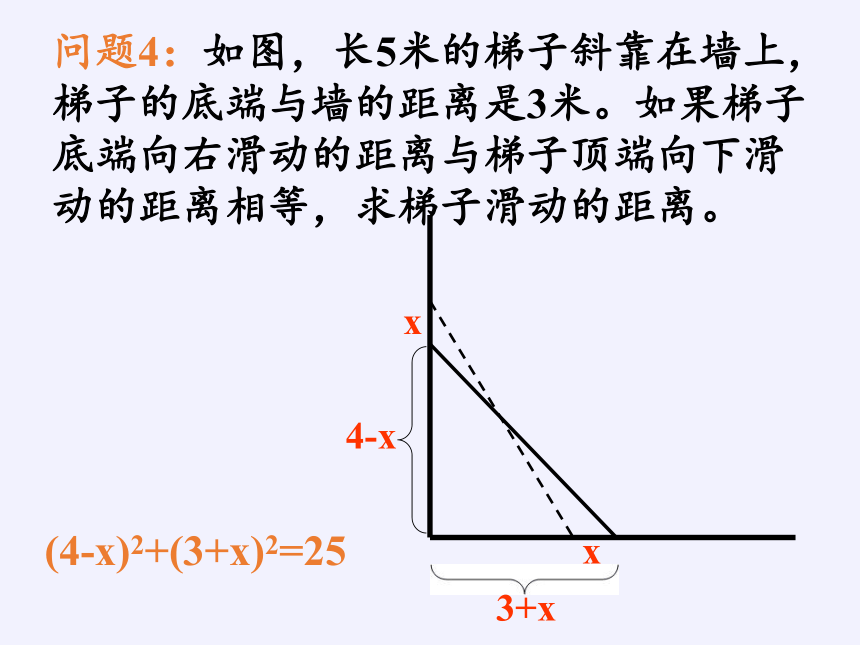
问题4:如图,长5米的梯子斜靠在墙上,梯子的底端与墙的距离是3米。如果梯子底端向右滑动的距离与梯子顶端向下滑动的距离相等,求梯子滑动的距离。
x
x
4-x
3+x
(4-x)2+(3+x)2=25
1、这四个方程有什么共同特点呢?
2、什么是一元二次方程?
3、一元二次方程的一般形式是什么?
4、什么是一元二次方程的二次项、一次项、常数项?
5、什么叫一元二次方程的二次项系数、一次项系数?
交流反馈:
1、共同特点:
(1) 都是整式方程
(2) 只含有一个未知数
(3) 未知数的最高次数是2
2、定义:整式方程经化简后,只含有
一个未知数,并且未知数的最高次数
是2,这样的方程叫做一元二次方程 .
3、一元二次方程的一般形式:
ax2+bx+c=0(a、b、c是常数且a≠0)。
其中 ——二次项,
a ——— 二次项系数;
bx —— 一次项,
b —— 一次项系数,
C —— 常数项。
交流反馈:
例1:下列方程中哪些是一元二次方程?试说明理由。
1. 2x2-5x-6=0 2. x2-7xy+6=0
3. x+x3=7 4. x2 - x=0
5. x2-4=(x+2)2 6. =7
概念巩固
例2:写出下列一元二次方程的 二次项系数、一次项系数和常数项。
概念巩固
练一练:1、指出下列关于x的一元二次方程的二次项系数、一次项系数和常数项:
(1) 3x2-x=2
(2) 7x-3=2x2;
(3) 2x(x-1)=3(x+5)-4
(4) abx2+cx+d=2x (ab不为0)
(5) (m+n)x2= (m-n) (m+n不为0)
当a 满足条件_______时,关于x的方程
(a2-4)x2+(a+2)x=8是 一元二次方程;
当a 满足条件_______时,关于x的方程
(a2-4)x2+(a+2)x=8 是 一元一次方程.
思维提升:
与周围的同学交流你的收获和困惑
小结:
(1)已知关于x的方程ax2+bx+c=0(a不为0)有两个根为1和-1,
则a+b+c=_____, a-b+c=_______
思维拓展:
(2)已知关于x的方程ax2+bx+c=0(a不为0)中满足4a+2b+c=0,则方程必有一个根
为 。
若满足9a-3b+c=0,则方程必有一个根为 。
思维拓展:
探索:m、n为何值时,x 2m+n+3x m-n-4=0
是关于x的一元二次方程。
思维拓展:
思考:已知a是方程 x2-2011x+1=0的一个不为0的根,
谢 谢
1.1 一元二次方程
问题2:学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册,平均每年增长的增长率是多少?
问题1:正方形桌面的面积是2m2,设正方形的边长是x m,求它的边长。
x2=2
5(1+x)2=7.2
自学反馈:
问题3:如图, 矩形花圃一面靠墙,另外三面所围的栅栏的总长度是19米,如果花圃的面积是24平方米,求花圃的长与宽。
墙
x
19-2x
x(19-2x)=24
问题4:如图,长5米的梯子斜靠在墙上,梯子的底端与墙的距离是3米。如果梯子底端向右滑动的距离与梯子顶端向下滑动的距离相等,求梯子滑动的距离。
x
x
4-x
3+x
(4-x)2+(3+x)2=25
1、这四个方程有什么共同特点呢?
2、什么是一元二次方程?
3、一元二次方程的一般形式是什么?
4、什么是一元二次方程的二次项、一次项、常数项?
5、什么叫一元二次方程的二次项系数、一次项系数?
交流反馈:
1、共同特点:
(1) 都是整式方程
(2) 只含有一个未知数
(3) 未知数的最高次数是2
2、定义:整式方程经化简后,只含有
一个未知数,并且未知数的最高次数
是2,这样的方程叫做一元二次方程 .
3、一元二次方程的一般形式:
ax2+bx+c=0(a、b、c是常数且a≠0)。
其中 ——二次项,
a ——— 二次项系数;
bx —— 一次项,
b —— 一次项系数,
C —— 常数项。
交流反馈:
例1:下列方程中哪些是一元二次方程?试说明理由。
1. 2x2-5x-6=0 2. x2-7xy+6=0
3. x+x3=7 4. x2 - x=0
5. x2-4=(x+2)2 6. =7
概念巩固
例2:写出下列一元二次方程的 二次项系数、一次项系数和常数项。
概念巩固
练一练:1、指出下列关于x的一元二次方程的二次项系数、一次项系数和常数项:
(1) 3x2-x=2
(2) 7x-3=2x2;
(3) 2x(x-1)=3(x+5)-4
(4) abx2+cx+d=2x (ab不为0)
(5) (m+n)x2= (m-n) (m+n不为0)
当a 满足条件_______时,关于x的方程
(a2-4)x2+(a+2)x=8是 一元二次方程;
当a 满足条件_______时,关于x的方程
(a2-4)x2+(a+2)x=8 是 一元一次方程.
思维提升:
与周围的同学交流你的收获和困惑
小结:
(1)已知关于x的方程ax2+bx+c=0(a不为0)有两个根为1和-1,
则a+b+c=_____, a-b+c=_______
思维拓展:
(2)已知关于x的方程ax2+bx+c=0(a不为0)中满足4a+2b+c=0,则方程必有一个根
为 。
若满足9a-3b+c=0,则方程必有一个根为 。
思维拓展:
探索:m、n为何值时,x 2m+n+3x m-n-4=0
是关于x的一元二次方程。
思维拓展:
思考:已知a是方程 x2-2011x+1=0的一个不为0的根,
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
