人教版八年级上册第十一章全等三角形学案
文档属性
| 名称 | 人教版八年级上册第十一章全等三角形学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 586.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-06 00:00:00 | ||
图片预览

文档简介
第1课时
§11.1 全等三角形
教学目标
1.知道什么是全等形、全等三角形及全等三角形的对应元素;
2.知道全等三角形的性质,能用符号正确地表示两个三角形全等;
3.能熟练找出两个全等三角形的对应角、对应边.
教学重点:全等三角形的性质.
教学难点:找全等三角形的对应边、对应角.
教学过程
Ⅰ.提出问题,创设情境
1.观察下列图案,指出这些图案中中形状与大小相同的图形
2.学生自己动手(同桌两名同学配合)
取一张纸,将自己事先准备好的三角板按在纸上,画下图形,照图形裁下来,纸样与三角板 、 完全一样.
3.获取概念
形状与大小都完全相同的两个图形就是 .(要是把两个图形放在一起,能够完全重合,就可以说明这两个图形的形状、大小相同.)
即:全等形的准确定义:能够完全重合的两个图形叫做全等形.
推得出全等三角形的概念:
对应顶点: 、对应角: 、
对应边: 。 “全等”符号: 读作“全等于”
Ⅱ.导入新课
将△ABC沿直线BC平移得△DEF;将△ABC沿BC翻折180°得到△DBC;将△ABC旋转180°得△AED.
议一议:各图中的两个三角形全等吗?
不难得出: ≌△DEF,△ABC≌ ,△ABC≌ .
(注意强调书写时对应顶点字母写在对应的位置上)
启示:一个图形经过平移、翻折、旋转后,位置变化了,但 、 都没有改变,所以平移、翻折、旋转前后的图形 ,这也是我们通过运动的方法寻求全等的一种策略.
观察与思考:寻找甲图中两三角形的对应元素,它们的对应边有什么关系?对应角呢?
全等三角形的性质: , 。
[例1]如图,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角.
[例2]如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.
(1)全等三角形对应角所对的边是对应边;两个对应角所夹的边也是对应边.
(2)全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角.
[例3]已知如图△ABC≌△ADE,试找出对应边、对应角.
Ⅲ.课堂练习
(1)下面是两个全等的三角形,按下列图形的位置摆放,指出它们的对应顶点、对应边、对应角
(2)如图,AB与AC,AD与AE是对应边,已知:,求的大小。
Ⅳ.课时小结
Ⅴ.作业1.教材:第四页习题:第1题,第2题
1.如果ΔABC≌ΔDEF,则AB的对应边是_____,AC的对应边是_____,∠C的对应角是_____,∠DEF的对应角是_____.
2.如图,ΔABC≌ΔDCB.(1)若∠D=74°
∠DBC=38°,则∠A=_____,∠ABC=_____
(2)如果AC=DB,请指出其他的对应边_____;
(3)如果ΔAOB≌ΔDOC,请指出所有的对应边_____,对应角_____.
3.如图,已知△ABE≌△DCE,AE=2 cm,BE=1.5 cm,
∠A=25°,∠B=48°;那么DE=_____cm,
EC=_____cm,∠C=_____°;∠D=_____°.
4.一个图形经过平移、翻折、旋转后,_____变化了,但__________都没有改变,即平移、翻折、旋转前后的图形
5. 已知:如图,以B为中心,将Rt△EBC绕B点逆时针旋转90°得到△ABD,若∠E=35°,求∠ADB的度数.
6、如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为
7、.已知:如图,△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
8、如图,AB⊥BC,ΔABE≌ΔECD.判断AE与DE的关系,并证明你的结论.
11.2三角形全等的判定 (1)
【学习目标】
1、三角形全等的“边边边”的条件,了解三角形的稳定性.
2、经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,做最佳自己
教学重点:三角形全等的条件.
教学难点:寻求三角形全等的条件.
【学习过程】
一、自主学习
1、复习:什么是全等三角形?全等三角形有些什么性质?
如图,△ABC≌△A′B′C′那么
相等的边是:
相等的角是:
2、讨论三角形全等的条件(动手画一画并回答下列问题)
(1).只给一个条件:一组对应边相等(或一组对应角相等),画出的两个三角形一定全等吗?
(2).给出两个条件画三角形,有____种情形。按下面给出的两个条件,画出的两个三角形一定全等吗?
①一组对应边相等和一组对应角相等
②两组对应边相等
③两组对应角相等
(3)、给出三个条件画三角形,有____种情形。按下面给出三个条件,画出的两个三角形一定全等吗?
①三组对应角相等
②三组对应边相等
已知一个三角形的三条边长分别为6cm、8cm、10cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
a.作图方法:
b.以小组为单位,把剪下的三角形重叠在一起,发现 ,这说明这些三角形都是 的.
c.归纳:三边对应相等的两个三角形 ,简写 ( http: / / www.xkb1.com )为“ ”或“ ”.
d、用数学语言表述:
在△ABC和中,
∵ ∴△ABC≌
用上面的规律可以判断两个三角形 .判断 ,叫做证明三角形全等.所以“SSS”是证明三角形全等的一个依据.
3、你能解释三角形为什么具有稳定性吗
二、合作探究
1、[例]如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
温馨提示:证明的书写步骤:
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
A、写出在哪两个三角形中,B、摆出三个条件用大括号括起来,C、写出全等结论。
2、尺规作图。
已知:∠AOB. 求作:∠DEF,使∠DEF=∠AOB
三、学以致用
1、如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌ △ ADE。
2、已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC
四、当堂检测
下列说法中,错误的有( )个
(1)周长相等的两个三角形全等。(2)周长相等的两个等边三角形全等。(3)有三个角对应相等的两个三角形全等。(4)有三边对应相等的两个三角形全等
A、1 B、2 C、3 D、4
2、已知:如图2-1,△RPQ中,RP=RQ,M为PQ的中点.
求证:RM平分∠PRQ.
分析:要证RM平分∠PRQ,即∠PRM=______,
只要证______≌______
证明:∵ M为PQ的中点(已知),
∴______=______
在△______和△______中,
∴______≌______( ).
∴ ∠PRM=______(______).
即:RM平分∠PRQ
3、已知:如图2-2,AB=DE,AC=DF,BE=CF.
求证:∠A=∠D.
分析:要证∠A=∠D,只要证______≌______.
证明:∵BE=CF ( ),
∴BC=______.
在△ABC和△DEF中,
∴______≌______( ).
∴ ∠A=∠D (______).
4、如图2-3,CE=DE,EA=EB,CA=DB,
求证:△ABC≌△BAD.
五、小结提高
六、作业:1、第15页习题11.2 1-2 2、第16页第9题
补充作业:
1、已知:如图2-4,AD=BC.AC=BD.试证明:∠CAD=∠DBC.
2、已知:如图,AD=BC,AB=DC,求证:∠A=∠C.
3、已知:如图,AB=EF,BC=FD,AD=EC,求证:∠B=∠F.
4、如图,在△ABC中,AB=AC,D、E两点在BC上,且有AD=AE,BD=CE,若∠BAD=30°,∠DAE=50°,求∠BAC的度数为
11.2三角形全等的判定(2)
【学习目标】
1、掌握三角形全等的“SAS”条件,能运用“SAS”证明简单的三角形全等问题
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,做最佳自己。
教学重点:三角形全等的条件.
教学难点:寻求三角形全等的条件.
【学习过程】
一、自主学习
1、复习思考
(1)怎样的两个三角形是全等三角形?全等三角形的性质是什么?三角形全等的判定(一)的内容是什么?
(2)上节课我们知道满足三个条件画两个三角形有4种情形,三个角对应相等;三条边对应相等;两角和一边对应相等;两边和一角对应相等;前两种情况已经研究了,今天我们来研究第三种两边和一角的情况,这种情况又要分两边和它们的夹角,两边及其一边的对角两种情况。
2、探究一:两边和它们的夹角对应相等的两个三角形是否全等?
(1)动手试一试
已知:△ABC
求作:,使,,
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(二):
两边和它们的夹角对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(二)
在△ABC和中,
∵ ∴△ABC≌
3、探究二:两边及其一边的对角对应相等的两个三角形是否全等?
通过画图或实验可以得出:
二、合作探究
1、已知:AD=CD,BD平分∠ADC
求证:∠A=∠C
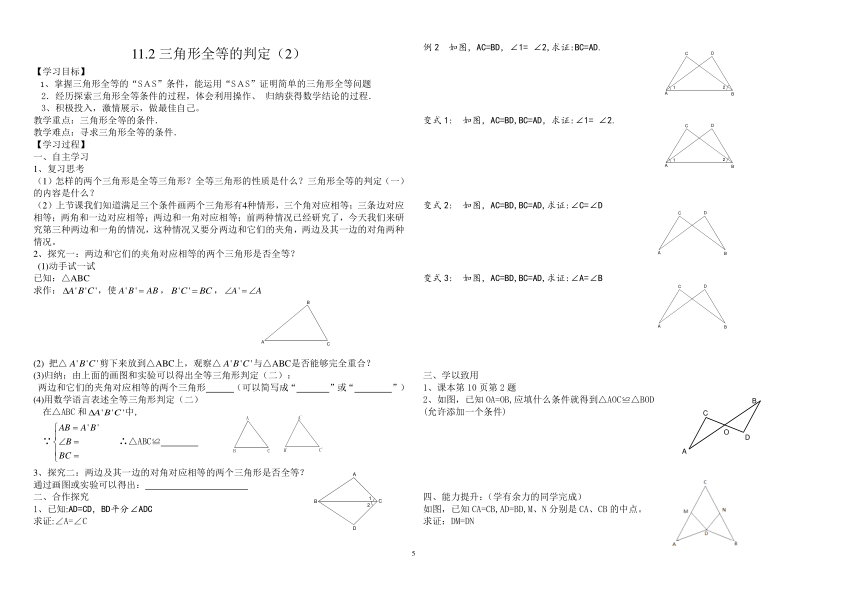
例2 如图,AC=BD,∠1= ∠2,求证:BC=AD.
变式1: 如图,AC=BD,BC=AD,求证:∠1= ∠2.
变式2: 如图,AC=BD,BC=AD,求证:∠C=∠D
变式3: 如图,AC=BD,BC=AD,求证:∠A=∠B
三、学以致用
1、课本第10页第2题
2、如图,已知OA=OB,应填什么条件就得到△AOC≌△BOD
(允许添加一个条件)
四、能力提升:(学有余力的同学完成)
如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点。
求证:DM=DN
五、当堂检测
1、如图,AD⊥BC,D为BC的中点,那么结论正确的有
A、△ABD≌△ACD B、∠B=∠C C、AD平分∠BAC D、△ABC是等边三角形
2.已知:如图,AB、CD相交于O点,AO=CO,OD=OB.
求证:∠D=∠B.
分析:要证∠D=∠B,只要证______≌______
证明:在△AOD与△COB中,
∴ △AOD≌△______ ( ).
∴ ∠D=∠B (______).
3.已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
分析:要证AD∥BC,只要证∠______=∠______,
又需证______≌______.
证明:∵ AB∥CD ( ),
∴ ∠______=∠______ ( ),
在△______和△______中,
∴ Δ______≌Δ______ ( ).
∴ ∠______=∠______ ( ).
∴ ______∥______( ).
六、课堂小结
1、两边和它们的夹角对应相等的两个三角形全等。简写成“ ”或“ ”
2、到目前为止,我们一共探索出判定三角形全等的2种方法,它们分别是: 和
作业:第15页习题11.2 3-4 第16页第10题
补充作业:
1、已知:如图3-3,AB=AC,∠BAD=∠CAD.
求证:∠B=∠C.
2、已知:如图3-4,AB=AC,BE=CD.
求证:∠B=∠C.
3、已知:如图3-5,AB=AD,AC=AE,∠1=∠2.
求证:BC=DE.
4、如图3-6,将两个一大、一小的等腰直角三角尺拼接 (A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.
11.2三角形全等的判定(3)
【学习目标】
1、掌握三角形全等的“角边角”“角角边”条件.能运用全等三角形的条件,解决简单的推理证明问题
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,体验成功的快乐。
教学重点:已知两角一边的三角形全等探究.
教学难点:灵活运用三角形全等条件证明.
【学习过程】
一、自主学习
1、复习思考
(1).到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?
(2).在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?三角形中已知两角一边又分成哪两种呢?
2、探究一:两角和它们的夹边对应相等的两个三角形是否全等?
(1)动手试一试。
已知:△ABC
求作:△,使=∠B, =∠C,=BC,(不写作法,保留作图痕迹)
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(三):
两角和它们的夹边对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(三)
在△ABC和中,
∵ ∴△ABC≌
3、探究二。两角和其中一角的对边对应相等的两三角形是否全等
(1)如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用前面学过的判定方法来证明你的结论吗?
(2)归纳;由上面的证明可以得出全等三角形判定(四):
两个角和其中一角的对边对应相等的两个三角形 (可以简写成“ ”或“ ”)
(3)用数学语言表述全等三角形判定(四)
在△ABC和中,
∵ ∴△ABC≌
二、合作探究
1、已知:如图,PM=PN,∠M=∠N.求证:AM=BN.
分析:∵PM=PN,∴ 要证AM=BN,只要证PA=______,
只要证______≌______.
证明:在△______与△______中,
∴ △______≌△______ ( ).
∴PA=______ ( ).
∵PM=PN ( ),
∴PM-______=PN-______,即AM=______.
2、已知:如图,ACBD.求证:OA=OB,OC=OD.
分析:要证OA=OB,OC=OD,只要证______≌______.
证明:∵ AC∥BD,∴ ∠C=______.
在△______与△______中,
∴______≌______ ( ).
∴ OA=OB,OC=OD ( ).
1、例1、如下图,D在AB上,E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
2.已知:点D在AB上,点E在AC上,∠BAO=∠CAO ,BE⊥AC, CD⊥AB,相交于点O,AB=AC, 求证:BD=CE
三、学以致用
1、课本第13页第1题
2、如图,在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,求证AB=AC+AD
六、课堂小结
(1)今天我们又学习了两个判定三角形全等的方法是:
(2)三角形全等的判定方法共有
(3)会根据已知两角及一边画三角形
作业:第15页习题11.2 5-6 第16页第11-12题
补充作业:
1、能确定△ABC≌△DEF的条件是 ( )
A.AB=DE,BC=EF,∠A=∠E B.AB=DE,BC=EF,∠C=∠E
C.∠A=∠E,AB=EF,∠B=∠D D.∠A=∠D,AB=DE,∠B=∠E
2、如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中,和△ABC全等的图形是 ( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
3、阅读下题及一位同学的解答过程:如图4-4,
AB和CD相交于点O,且OA=OB,∠A=∠C.
那么△AOD与△COB全等吗?若全等,
试写出证明过程;若不全等,请说明理由.
答:△AOD≌△COB.
证明:在△AOD和△COB中,
∴ △AOD≌△COB (ASA).
问:这位同学的回答及证明过程正确吗?为什么?
4.已知:如图4-5,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.
求证:AD=AC.
图4-5
5、已知:如图4-6,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.
求证:HN=PM.
图4-6
6、已知ΔABC≌ΔA'B'C',AD、A'D'分别是ΔABC和ΔA'B'C'的角平分线.
(1)请证明AD=A'D';
(2)把上述结论用文字叙述出来;
(3)你还能得出其他类似的结论吗?
第5课时
11.2三角形全等的判定(4)
【学习目标】
1、理解直角三角形全等的判定方法“HL”,并能灵活选择方法判定三角形全等;
2.通过独立思考、小组合作、展示质疑,体会探索数学结论的过程,发展合情推理能力;
3. 极度热情、高度责任、自动自发、享受成功。
教学重点:运用直角三角形全等的条件解决一些实际问题。
教学难点:熟练运用直角三角形全等的条件解决一些实际问题。
【学习过程】
一、自主学习
1、复习思考
(1)、判定两个三角形全等的方法: 、 、 、
(2)、如图,Rt△ABC中,直角边是 、 ,斜边是
(3)、如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
②若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
③若AB=DE,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
④若AB=DE,BC=EF,AC=DF
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
2、如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
(1)动手试一试。
已知:Rt△ABC
求作:Rt△, 使=90°, =AB, =BC
作法:
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法
斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述上面的判定方法
在Rt△ABC和Rt中,
∵ ∴Rt△ABC≌Rt△
(5)直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法 “ ”、
“ ”、 “ ”、 “ ”、 还有直角三角形特殊的判定方法 “ ”
二、合作探究
1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
2、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
三、学以致用
1、如图,△ABC中,AB=AC,AD是高,
则△ADB与△ADC (填“全等”或“不全等” )
根据 (用简写法)
2、判断两个直角三角形全等的方法不正确的有( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两个锐角对应相等
3、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵ AF⊥BC,DE⊥BC (已知)
∴ ∠AFB=∠DEC= °(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△ 和Rt△ 中
∵∴ ≌
( )
∴ = ( )
∴ (内错角相等,两直线平行)
4.如图5-1,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌_____,全等的根据是_____.
图5-1
5.判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和这个角的邻边对应相等;( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等. ( )
二、选择题
6.下列说法正确的是 ( )
A.一直角边对应相等的两个直角三角形全等
B.斜边相等的两个直角三角形全等
C.斜边相等的两个等腰直角三角形全等
D.一边长相等的两等腰直角三角形全等
四、当堂检测
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
五、课堂小结
这节课你有什么收获呢?与你的同伴进行交流
作业:第16页习题11.2 7-8 第17页第13题
补充作业:
1.已知:如图5-3,AB⊥BD,CD⊥BD,AD=BC.
求证:(1)AB=DC:
(2)AD∥BC.
图5-3
2.已知:如图5-4,AC=BD,AD⊥AC,BC⊥BD.
求证:AD=BC;
3、能力提升:(学有余力的同学完成)
如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。(1)求证:MB=MD,ME=MF;(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。
第6课时
11.3角的平分线的性质(1)
【学习目标】
1、经历角的平分线性质的发现过程,初步掌握角的平分线的性质定理.
2、能运用角的平分线性质定理解决简单的几何问题.
3、极度热情、高度责任、自动自发、享受成功。
教学重点:掌握角的平分线的性质定理
教学难点: 角平分线定理的应用。
【学习过程】
一、自主学习
1、复习思考
什么是角的平分线?怎样画一个角的平分线?
2.如右图,AB=AD,BC=DC, 沿着A、C画一条射线AE,AE就是∠BAD的角平分线,你知道为什么吗
3.根据角平分仪的制作原理,如何用尺规作角的平分线?自学课本19页后,思考为什么要用大于MN的长为半径画弧?
4.OC是∠AOB的平分线,点P是射线OC上的任意一点,
操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:观察测量结果,猜想线段PD与PE的大小关系,写出结论
PD PE
第一次
第二次
第三次
5、命题:角平分线上的点到这个角的两边距离相等.
题设:一个点在一个角的平分线上
结论:这个点到这个角的两边的距离相等
结合第4题图形请你写出已知和求证,并证明命题的正确性
解后思考:证明一个几何命题的步骤有那些?
6、用数学语言来表述角的平分线的性质定理:
如右上图,∵OC是∠AOB的平分线,点P是
∴
二、合作探究
1、如图所示OC是∠AOB 的平分线,P 是OC上任意一点,问PE=PD 为什么
2、如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB
三、学以致用
在Rt△ABC中,BD平分∠ABC, DE⊥AB于E,则
⑴图中相等的线段有哪些?相等的角呢?
⑵哪条线段与DE相等?为什么?
⑶若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长。
四、当堂检测
如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长
五、课堂小结
这节课你有什么收获呢?与你的同伴进行交流
六、作业:
第22页习题11.3 1-2 第23页第4-5题
基础闯关
1.在△ABC中,∠C=90°,AD是∠BAC的角平分线,若BC=5㎝,BD=3㎝,则点D到AB的距离为_____________。
2.∠AOB的平分线上一点M,M到OA的距离为1.5㎝,则M到OB的距离为_______㎝。
3.如图,∠A=90°,BD是△ABC的角平分线,
AC=8㎝,DC=3DA,则点D到BC的距离为 __________。
4.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,
下列结论错误的是( )
A、PD=PE B、OD=OE C、∠DPO=∠EPO D、PD=OD
5.三角形中到三边距离相等的点是( )
A、三条边的垂直平分线的交点 B、三条高的交点
C、三条中线的交点 D、三条角平分线的交点
6.如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC,
求证:BE=CF。
7.已知,如图BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于D.
求证:PM=PN。
能力提升
8.如图,△ABC中,∠C=90°,AC=BC,
AD平分∠CAB交BC于D,DE⊥AB于E,
且AB=6㎝。
求:△DEB的周长
9.如图,MP⊥NP,MQ为△MNP的角平分线,
MT=MP,连接TQ,则下列结论中不正确的是( )
A、TQ=PQ B、∠MQT=∠MQP
C、∠QTN=90° D、∠NQT=∠MQT
第7课时
11.3角的平分线的性质(2)
【学习目标】
1、会叙述角的平分线的性质及“到角两边距离相等的点在角的平分线上”.
2、能应用这两个性质解决一些简单的实际问题.
3、极度热情、高度责任、自动自发、享受成功。
教学重点:角平分线的性质及其应用
教学难点: 灵活应用两个性质解决问题。
【学习过程】
一、自主学习
1、复习思考(1)、画出三角形三个内角的平分线
你发现了什么特点吗?
(2)、如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB,BC,CA的距离相等。
2、求证:到角的两边的距离相等的点在角的平分线上。
(提示:先画图,并写出已知、求证,再加以证明)
3、要在S区建一个集贸市场,使它到公路,铁路
距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)
二、合作探究
1、比较角平分线的性质与判定
2、如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证∠1=∠2
三、学以致用 22页练习题
四、能力提高
1、如图,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,求证:∠A+∠C=180°
五、课堂小结
这节课你有什么收获呢?与你的同伴进行交流
六、作业
1、已知△ABC中,∠A=60°,∠ABC,∠ACB的平分线交于点O,则∠BOC的度数为
2、下列说法错误的是( )
A、到已知角两边距离相等的点都在同一条直线上
B、一条直线上有一点到已知角的两边的距离相等,则这条直线平分已知角
C、到已知角两边距离相等的点与角的顶点的连线平分已知角
D、已知角内有两点各自到两边的距离相等,经过这两点的直线平分已知角
3、到三角形三条边的距离相等的点是( )
A、三条中线的交点 B、三条高线的交点
C、三条边的垂直平分线的交点 D、三条角平分线的交点
4、课本23页第6题
10.如图,B是∠CAF内一点,D在AC上,E在AF上,且DC=EF,△BCD与△BEF的面积相等。求证:AB平分∠CAF。
考题追踪
1、(安徽)如图,直线 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、1处 B、2处 C、3处 D、4处
2.(山东)如图,某铁路MN与公路PQ相交
于点O且交角为90°,某仓库G在A区,到公、铁路
距离相等,且到公路与铁路的相交点O的距离为200m。
⑴在图上标出仓库G的位置。(比例尺:1:10000。用尺规作图,保留作图痕迹,不写作法)
⑵求出仓库G到铁路的实际距离。
3.如图,∠AOB是直角,OP平分∠AOB,OQ平分∠AOC,∠POQ=70o ,求∠AOC的度数.
4.如图,BD=CD,BF⊥AC,CE⊥AB.求证:D在∠BAC的角平分线上.
5. 如图,在△ABC中,∠B=∠C,点D是BC的中点,DE⊥AB,DF⊥AC,E,F为垂足,求证:D在∠BAC的角平分线上.
6、已知:如图,Rt△ABC中,∠C=90度,AC=BC,AD为∠BAC的平分线,AE=BC,DE⊥AB垂足为E,求证△DBE的周长等于AB.
7、如图,AE平分∠BAC,BD=DC,DE⊥BC,EM⊥AB,EN⊥AC.求证:BM=CN.
B
C
D
E
O
A
C
D
B
C
A
O
B
D
A
B
C
D
A
B
C
A1
B1
C1
O
A
B
E
D
C
P
E
D
C
B
A
E
D
C
B
A
PAGE
14
§11.1 全等三角形
教学目标
1.知道什么是全等形、全等三角形及全等三角形的对应元素;
2.知道全等三角形的性质,能用符号正确地表示两个三角形全等;
3.能熟练找出两个全等三角形的对应角、对应边.
教学重点:全等三角形的性质.
教学难点:找全等三角形的对应边、对应角.
教学过程
Ⅰ.提出问题,创设情境
1.观察下列图案,指出这些图案中中形状与大小相同的图形
2.学生自己动手(同桌两名同学配合)
取一张纸,将自己事先准备好的三角板按在纸上,画下图形,照图形裁下来,纸样与三角板 、 完全一样.
3.获取概念
形状与大小都完全相同的两个图形就是 .(要是把两个图形放在一起,能够完全重合,就可以说明这两个图形的形状、大小相同.)
即:全等形的准确定义:能够完全重合的两个图形叫做全等形.
推得出全等三角形的概念:
对应顶点: 、对应角: 、
对应边: 。 “全等”符号: 读作“全等于”
Ⅱ.导入新课
将△ABC沿直线BC平移得△DEF;将△ABC沿BC翻折180°得到△DBC;将△ABC旋转180°得△AED.
议一议:各图中的两个三角形全等吗?
不难得出: ≌△DEF,△ABC≌ ,△ABC≌ .
(注意强调书写时对应顶点字母写在对应的位置上)
启示:一个图形经过平移、翻折、旋转后,位置变化了,但 、 都没有改变,所以平移、翻折、旋转前后的图形 ,这也是我们通过运动的方法寻求全等的一种策略.
观察与思考:寻找甲图中两三角形的对应元素,它们的对应边有什么关系?对应角呢?
全等三角形的性质: , 。
[例1]如图,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角.
[例2]如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.
(1)全等三角形对应角所对的边是对应边;两个对应角所夹的边也是对应边.
(2)全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角.
[例3]已知如图△ABC≌△ADE,试找出对应边、对应角.
Ⅲ.课堂练习
(1)下面是两个全等的三角形,按下列图形的位置摆放,指出它们的对应顶点、对应边、对应角
(2)如图,AB与AC,AD与AE是对应边,已知:,求的大小。
Ⅳ.课时小结
Ⅴ.作业1.教材:第四页习题:第1题,第2题
1.如果ΔABC≌ΔDEF,则AB的对应边是_____,AC的对应边是_____,∠C的对应角是_____,∠DEF的对应角是_____.
2.如图,ΔABC≌ΔDCB.(1)若∠D=74°
∠DBC=38°,则∠A=_____,∠ABC=_____
(2)如果AC=DB,请指出其他的对应边_____;
(3)如果ΔAOB≌ΔDOC,请指出所有的对应边_____,对应角_____.
3.如图,已知△ABE≌△DCE,AE=2 cm,BE=1.5 cm,
∠A=25°,∠B=48°;那么DE=_____cm,
EC=_____cm,∠C=_____°;∠D=_____°.
4.一个图形经过平移、翻折、旋转后,_____变化了,但__________都没有改变,即平移、翻折、旋转前后的图形
5. 已知:如图,以B为中心,将Rt△EBC绕B点逆时针旋转90°得到△ABD,若∠E=35°,求∠ADB的度数.
6、如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为
7、.已知:如图,△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
8、如图,AB⊥BC,ΔABE≌ΔECD.判断AE与DE的关系,并证明你的结论.
11.2三角形全等的判定 (1)
【学习目标】
1、三角形全等的“边边边”的条件,了解三角形的稳定性.
2、经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,做最佳自己
教学重点:三角形全等的条件.
教学难点:寻求三角形全等的条件.
【学习过程】
一、自主学习
1、复习:什么是全等三角形?全等三角形有些什么性质?
如图,△ABC≌△A′B′C′那么
相等的边是:
相等的角是:
2、讨论三角形全等的条件(动手画一画并回答下列问题)
(1).只给一个条件:一组对应边相等(或一组对应角相等),画出的两个三角形一定全等吗?
(2).给出两个条件画三角形,有____种情形。按下面给出的两个条件,画出的两个三角形一定全等吗?
①一组对应边相等和一组对应角相等
②两组对应边相等
③两组对应角相等
(3)、给出三个条件画三角形,有____种情形。按下面给出三个条件,画出的两个三角形一定全等吗?
①三组对应角相等
②三组对应边相等
已知一个三角形的三条边长分别为6cm、8cm、10cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
a.作图方法:
b.以小组为单位,把剪下的三角形重叠在一起,发现 ,这说明这些三角形都是 的.
c.归纳:三边对应相等的两个三角形 ,简写 ( http: / / www.xkb1.com )为“ ”或“ ”.
d、用数学语言表述:
在△ABC和中,
∵ ∴△ABC≌
用上面的规律可以判断两个三角形 .判断 ,叫做证明三角形全等.所以“SSS”是证明三角形全等的一个依据.
3、你能解释三角形为什么具有稳定性吗
二、合作探究
1、[例]如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
温馨提示:证明的书写步骤:
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
A、写出在哪两个三角形中,B、摆出三个条件用大括号括起来,C、写出全等结论。
2、尺规作图。
已知:∠AOB. 求作:∠DEF,使∠DEF=∠AOB
三、学以致用
1、如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌ △ ADE。
2、已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC
四、当堂检测
下列说法中,错误的有( )个
(1)周长相等的两个三角形全等。(2)周长相等的两个等边三角形全等。(3)有三个角对应相等的两个三角形全等。(4)有三边对应相等的两个三角形全等
A、1 B、2 C、3 D、4
2、已知:如图2-1,△RPQ中,RP=RQ,M为PQ的中点.
求证:RM平分∠PRQ.
分析:要证RM平分∠PRQ,即∠PRM=______,
只要证______≌______
证明:∵ M为PQ的中点(已知),
∴______=______
在△______和△______中,
∴______≌______( ).
∴ ∠PRM=______(______).
即:RM平分∠PRQ
3、已知:如图2-2,AB=DE,AC=DF,BE=CF.
求证:∠A=∠D.
分析:要证∠A=∠D,只要证______≌______.
证明:∵BE=CF ( ),
∴BC=______.
在△ABC和△DEF中,
∴______≌______( ).
∴ ∠A=∠D (______).
4、如图2-3,CE=DE,EA=EB,CA=DB,
求证:△ABC≌△BAD.
五、小结提高
六、作业:1、第15页习题11.2 1-2 2、第16页第9题
补充作业:
1、已知:如图2-4,AD=BC.AC=BD.试证明:∠CAD=∠DBC.
2、已知:如图,AD=BC,AB=DC,求证:∠A=∠C.
3、已知:如图,AB=EF,BC=FD,AD=EC,求证:∠B=∠F.
4、如图,在△ABC中,AB=AC,D、E两点在BC上,且有AD=AE,BD=CE,若∠BAD=30°,∠DAE=50°,求∠BAC的度数为
11.2三角形全等的判定(2)
【学习目标】
1、掌握三角形全等的“SAS”条件,能运用“SAS”证明简单的三角形全等问题
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,做最佳自己。
教学重点:三角形全等的条件.
教学难点:寻求三角形全等的条件.
【学习过程】
一、自主学习
1、复习思考
(1)怎样的两个三角形是全等三角形?全等三角形的性质是什么?三角形全等的判定(一)的内容是什么?
(2)上节课我们知道满足三个条件画两个三角形有4种情形,三个角对应相等;三条边对应相等;两角和一边对应相等;两边和一角对应相等;前两种情况已经研究了,今天我们来研究第三种两边和一角的情况,这种情况又要分两边和它们的夹角,两边及其一边的对角两种情况。
2、探究一:两边和它们的夹角对应相等的两个三角形是否全等?
(1)动手试一试
已知:△ABC
求作:,使,,
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(二):
两边和它们的夹角对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(二)
在△ABC和中,
∵ ∴△ABC≌
3、探究二:两边及其一边的对角对应相等的两个三角形是否全等?
通过画图或实验可以得出:
二、合作探究
1、已知:AD=CD,BD平分∠ADC
求证:∠A=∠C
例2 如图,AC=BD,∠1= ∠2,求证:BC=AD.
变式1: 如图,AC=BD,BC=AD,求证:∠1= ∠2.
变式2: 如图,AC=BD,BC=AD,求证:∠C=∠D
变式3: 如图,AC=BD,BC=AD,求证:∠A=∠B
三、学以致用
1、课本第10页第2题
2、如图,已知OA=OB,应填什么条件就得到△AOC≌△BOD
(允许添加一个条件)
四、能力提升:(学有余力的同学完成)
如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点。
求证:DM=DN
五、当堂检测
1、如图,AD⊥BC,D为BC的中点,那么结论正确的有
A、△ABD≌△ACD B、∠B=∠C C、AD平分∠BAC D、△ABC是等边三角形
2.已知:如图,AB、CD相交于O点,AO=CO,OD=OB.
求证:∠D=∠B.
分析:要证∠D=∠B,只要证______≌______
证明:在△AOD与△COB中,
∴ △AOD≌△______ ( ).
∴ ∠D=∠B (______).
3.已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
分析:要证AD∥BC,只要证∠______=∠______,
又需证______≌______.
证明:∵ AB∥CD ( ),
∴ ∠______=∠______ ( ),
在△______和△______中,
∴ Δ______≌Δ______ ( ).
∴ ∠______=∠______ ( ).
∴ ______∥______( ).
六、课堂小结
1、两边和它们的夹角对应相等的两个三角形全等。简写成“ ”或“ ”
2、到目前为止,我们一共探索出判定三角形全等的2种方法,它们分别是: 和
作业:第15页习题11.2 3-4 第16页第10题
补充作业:
1、已知:如图3-3,AB=AC,∠BAD=∠CAD.
求证:∠B=∠C.
2、已知:如图3-4,AB=AC,BE=CD.
求证:∠B=∠C.
3、已知:如图3-5,AB=AD,AC=AE,∠1=∠2.
求证:BC=DE.
4、如图3-6,将两个一大、一小的等腰直角三角尺拼接 (A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.
11.2三角形全等的判定(3)
【学习目标】
1、掌握三角形全等的“角边角”“角角边”条件.能运用全等三角形的条件,解决简单的推理证明问题
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,体验成功的快乐。
教学重点:已知两角一边的三角形全等探究.
教学难点:灵活运用三角形全等条件证明.
【学习过程】
一、自主学习
1、复习思考
(1).到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?
(2).在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?三角形中已知两角一边又分成哪两种呢?
2、探究一:两角和它们的夹边对应相等的两个三角形是否全等?
(1)动手试一试。
已知:△ABC
求作:△,使=∠B, =∠C,=BC,(不写作法,保留作图痕迹)
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(三):
两角和它们的夹边对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(三)
在△ABC和中,
∵ ∴△ABC≌
3、探究二。两角和其中一角的对边对应相等的两三角形是否全等
(1)如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用前面学过的判定方法来证明你的结论吗?
(2)归纳;由上面的证明可以得出全等三角形判定(四):
两个角和其中一角的对边对应相等的两个三角形 (可以简写成“ ”或“ ”)
(3)用数学语言表述全等三角形判定(四)
在△ABC和中,
∵ ∴△ABC≌
二、合作探究
1、已知:如图,PM=PN,∠M=∠N.求证:AM=BN.
分析:∵PM=PN,∴ 要证AM=BN,只要证PA=______,
只要证______≌______.
证明:在△______与△______中,
∴ △______≌△______ ( ).
∴PA=______ ( ).
∵PM=PN ( ),
∴PM-______=PN-______,即AM=______.
2、已知:如图,ACBD.求证:OA=OB,OC=OD.
分析:要证OA=OB,OC=OD,只要证______≌______.
证明:∵ AC∥BD,∴ ∠C=______.
在△______与△______中,
∴______≌______ ( ).
∴ OA=OB,OC=OD ( ).
1、例1、如下图,D在AB上,E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
2.已知:点D在AB上,点E在AC上,∠BAO=∠CAO ,BE⊥AC, CD⊥AB,相交于点O,AB=AC, 求证:BD=CE
三、学以致用
1、课本第13页第1题
2、如图,在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,求证AB=AC+AD
六、课堂小结
(1)今天我们又学习了两个判定三角形全等的方法是:
(2)三角形全等的判定方法共有
(3)会根据已知两角及一边画三角形
作业:第15页习题11.2 5-6 第16页第11-12题
补充作业:
1、能确定△ABC≌△DEF的条件是 ( )
A.AB=DE,BC=EF,∠A=∠E B.AB=DE,BC=EF,∠C=∠E
C.∠A=∠E,AB=EF,∠B=∠D D.∠A=∠D,AB=DE,∠B=∠E
2、如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中,和△ABC全等的图形是 ( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
3、阅读下题及一位同学的解答过程:如图4-4,
AB和CD相交于点O,且OA=OB,∠A=∠C.
那么△AOD与△COB全等吗?若全等,
试写出证明过程;若不全等,请说明理由.
答:△AOD≌△COB.
证明:在△AOD和△COB中,
∴ △AOD≌△COB (ASA).
问:这位同学的回答及证明过程正确吗?为什么?
4.已知:如图4-5,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.
求证:AD=AC.
图4-5
5、已知:如图4-6,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.
求证:HN=PM.
图4-6
6、已知ΔABC≌ΔA'B'C',AD、A'D'分别是ΔABC和ΔA'B'C'的角平分线.
(1)请证明AD=A'D';
(2)把上述结论用文字叙述出来;
(3)你还能得出其他类似的结论吗?
第5课时
11.2三角形全等的判定(4)
【学习目标】
1、理解直角三角形全等的判定方法“HL”,并能灵活选择方法判定三角形全等;
2.通过独立思考、小组合作、展示质疑,体会探索数学结论的过程,发展合情推理能力;
3. 极度热情、高度责任、自动自发、享受成功。
教学重点:运用直角三角形全等的条件解决一些实际问题。
教学难点:熟练运用直角三角形全等的条件解决一些实际问题。
【学习过程】
一、自主学习
1、复习思考
(1)、判定两个三角形全等的方法: 、 、 、
(2)、如图,Rt△ABC中,直角边是 、 ,斜边是
(3)、如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
②若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
③若AB=DE,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
④若AB=DE,BC=EF,AC=DF
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
2、如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
(1)动手试一试。
已知:Rt△ABC
求作:Rt△, 使=90°, =AB, =BC
作法:
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法
斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述上面的判定方法
在Rt△ABC和Rt中,
∵ ∴Rt△ABC≌Rt△
(5)直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法 “ ”、
“ ”、 “ ”、 “ ”、 还有直角三角形特殊的判定方法 “ ”
二、合作探究
1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
2、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
三、学以致用
1、如图,△ABC中,AB=AC,AD是高,
则△ADB与△ADC (填“全等”或“不全等” )
根据 (用简写法)
2、判断两个直角三角形全等的方法不正确的有( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两个锐角对应相等
3、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵ AF⊥BC,DE⊥BC (已知)
∴ ∠AFB=∠DEC= °(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△ 和Rt△ 中
∵∴ ≌
( )
∴ = ( )
∴ (内错角相等,两直线平行)
4.如图5-1,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌_____,全等的根据是_____.
图5-1
5.判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和这个角的邻边对应相等;( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等. ( )
二、选择题
6.下列说法正确的是 ( )
A.一直角边对应相等的两个直角三角形全等
B.斜边相等的两个直角三角形全等
C.斜边相等的两个等腰直角三角形全等
D.一边长相等的两等腰直角三角形全等
四、当堂检测
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
五、课堂小结
这节课你有什么收获呢?与你的同伴进行交流
作业:第16页习题11.2 7-8 第17页第13题
补充作业:
1.已知:如图5-3,AB⊥BD,CD⊥BD,AD=BC.
求证:(1)AB=DC:
(2)AD∥BC.
图5-3
2.已知:如图5-4,AC=BD,AD⊥AC,BC⊥BD.
求证:AD=BC;
3、能力提升:(学有余力的同学完成)
如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。(1)求证:MB=MD,ME=MF;(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。
第6课时
11.3角的平分线的性质(1)
【学习目标】
1、经历角的平分线性质的发现过程,初步掌握角的平分线的性质定理.
2、能运用角的平分线性质定理解决简单的几何问题.
3、极度热情、高度责任、自动自发、享受成功。
教学重点:掌握角的平分线的性质定理
教学难点: 角平分线定理的应用。
【学习过程】
一、自主学习
1、复习思考
什么是角的平分线?怎样画一个角的平分线?
2.如右图,AB=AD,BC=DC, 沿着A、C画一条射线AE,AE就是∠BAD的角平分线,你知道为什么吗
3.根据角平分仪的制作原理,如何用尺规作角的平分线?自学课本19页后,思考为什么要用大于MN的长为半径画弧?
4.OC是∠AOB的平分线,点P是射线OC上的任意一点,
操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:观察测量结果,猜想线段PD与PE的大小关系,写出结论
PD PE
第一次
第二次
第三次
5、命题:角平分线上的点到这个角的两边距离相等.
题设:一个点在一个角的平分线上
结论:这个点到这个角的两边的距离相等
结合第4题图形请你写出已知和求证,并证明命题的正确性
解后思考:证明一个几何命题的步骤有那些?
6、用数学语言来表述角的平分线的性质定理:
如右上图,∵OC是∠AOB的平分线,点P是
∴
二、合作探究
1、如图所示OC是∠AOB 的平分线,P 是OC上任意一点,问PE=PD 为什么
2、如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB
三、学以致用
在Rt△ABC中,BD平分∠ABC, DE⊥AB于E,则
⑴图中相等的线段有哪些?相等的角呢?
⑵哪条线段与DE相等?为什么?
⑶若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长。
四、当堂检测
如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长
五、课堂小结
这节课你有什么收获呢?与你的同伴进行交流
六、作业:
第22页习题11.3 1-2 第23页第4-5题
基础闯关
1.在△ABC中,∠C=90°,AD是∠BAC的角平分线,若BC=5㎝,BD=3㎝,则点D到AB的距离为_____________。
2.∠AOB的平分线上一点M,M到OA的距离为1.5㎝,则M到OB的距离为_______㎝。
3.如图,∠A=90°,BD是△ABC的角平分线,
AC=8㎝,DC=3DA,则点D到BC的距离为 __________。
4.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,
下列结论错误的是( )
A、PD=PE B、OD=OE C、∠DPO=∠EPO D、PD=OD
5.三角形中到三边距离相等的点是( )
A、三条边的垂直平分线的交点 B、三条高的交点
C、三条中线的交点 D、三条角平分线的交点
6.如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC,
求证:BE=CF。
7.已知,如图BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于D.
求证:PM=PN。
能力提升
8.如图,△ABC中,∠C=90°,AC=BC,
AD平分∠CAB交BC于D,DE⊥AB于E,
且AB=6㎝。
求:△DEB的周长
9.如图,MP⊥NP,MQ为△MNP的角平分线,
MT=MP,连接TQ,则下列结论中不正确的是( )
A、TQ=PQ B、∠MQT=∠MQP
C、∠QTN=90° D、∠NQT=∠MQT
第7课时
11.3角的平分线的性质(2)
【学习目标】
1、会叙述角的平分线的性质及“到角两边距离相等的点在角的平分线上”.
2、能应用这两个性质解决一些简单的实际问题.
3、极度热情、高度责任、自动自发、享受成功。
教学重点:角平分线的性质及其应用
教学难点: 灵活应用两个性质解决问题。
【学习过程】
一、自主学习
1、复习思考(1)、画出三角形三个内角的平分线
你发现了什么特点吗?
(2)、如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB,BC,CA的距离相等。
2、求证:到角的两边的距离相等的点在角的平分线上。
(提示:先画图,并写出已知、求证,再加以证明)
3、要在S区建一个集贸市场,使它到公路,铁路
距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)
二、合作探究
1、比较角平分线的性质与判定
2、如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证∠1=∠2
三、学以致用 22页练习题
四、能力提高
1、如图,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,求证:∠A+∠C=180°
五、课堂小结
这节课你有什么收获呢?与你的同伴进行交流
六、作业
1、已知△ABC中,∠A=60°,∠ABC,∠ACB的平分线交于点O,则∠BOC的度数为
2、下列说法错误的是( )
A、到已知角两边距离相等的点都在同一条直线上
B、一条直线上有一点到已知角的两边的距离相等,则这条直线平分已知角
C、到已知角两边距离相等的点与角的顶点的连线平分已知角
D、已知角内有两点各自到两边的距离相等,经过这两点的直线平分已知角
3、到三角形三条边的距离相等的点是( )
A、三条中线的交点 B、三条高线的交点
C、三条边的垂直平分线的交点 D、三条角平分线的交点
4、课本23页第6题
10.如图,B是∠CAF内一点,D在AC上,E在AF上,且DC=EF,△BCD与△BEF的面积相等。求证:AB平分∠CAF。
考题追踪
1、(安徽)如图,直线 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、1处 B、2处 C、3处 D、4处
2.(山东)如图,某铁路MN与公路PQ相交
于点O且交角为90°,某仓库G在A区,到公、铁路
距离相等,且到公路与铁路的相交点O的距离为200m。
⑴在图上标出仓库G的位置。(比例尺:1:10000。用尺规作图,保留作图痕迹,不写作法)
⑵求出仓库G到铁路的实际距离。
3.如图,∠AOB是直角,OP平分∠AOB,OQ平分∠AOC,∠POQ=70o ,求∠AOC的度数.
4.如图,BD=CD,BF⊥AC,CE⊥AB.求证:D在∠BAC的角平分线上.
5. 如图,在△ABC中,∠B=∠C,点D是BC的中点,DE⊥AB,DF⊥AC,E,F为垂足,求证:D在∠BAC的角平分线上.
6、已知:如图,Rt△ABC中,∠C=90度,AC=BC,AD为∠BAC的平分线,AE=BC,DE⊥AB垂足为E,求证△DBE的周长等于AB.
7、如图,AE平分∠BAC,BD=DC,DE⊥BC,EM⊥AB,EN⊥AC.求证:BM=CN.
B
C
D
E
O
A
C
D
B
C
A
O
B
D
A
B
C
D
A
B
C
A1
B1
C1
O
A
B
E
D
C
P
E
D
C
B
A
E
D
C
B
A
PAGE
14
