2021-2022学年数学上学期人教A版必修1 2.2.2对数函数及其性质1 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年数学上学期人教A版必修1 2.2.2对数函数及其性质1 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 396.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 20:21:29 | ||
图片预览






文档简介
(共20张PPT)
2.2.2 对数函数及其性质(一)
问题: 某种细胞分裂时,由1个分裂为2个,2个分为4
个,……,一个这样的细胞分裂x次后,得到的细胞的
个数 y 与 x 的函数关系是:
现在我们来研究相反的问题.如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞,那么,分裂次数 x 就是要得到的细胞个数 y 的函数.
x=log2y
如果用x表示自变量,y表示函
数,这个函数就是 y=log2x.
1. 对数函数的定义:
函数 y=logax (a>0且a≠1)叫做
对数函数,其中x是自变量,函数的
定义域是
(0,+∞).
判断:下列函数是否为对数函数?
① y=logax2(a>0,且a≠1);
② y=log2x-1;
③ y=log2(x-1);
④ y=log5x;
⑤ y=logxa(x>0,且x≠1);
⑥ y=2log8x ;
⑦
【点拨】 一个函数为对数函数的条件是:
①系数为1;②底数为大于0且不等于1的常数;
③真数为单个自变量.
否
否
否
是
否
否
是
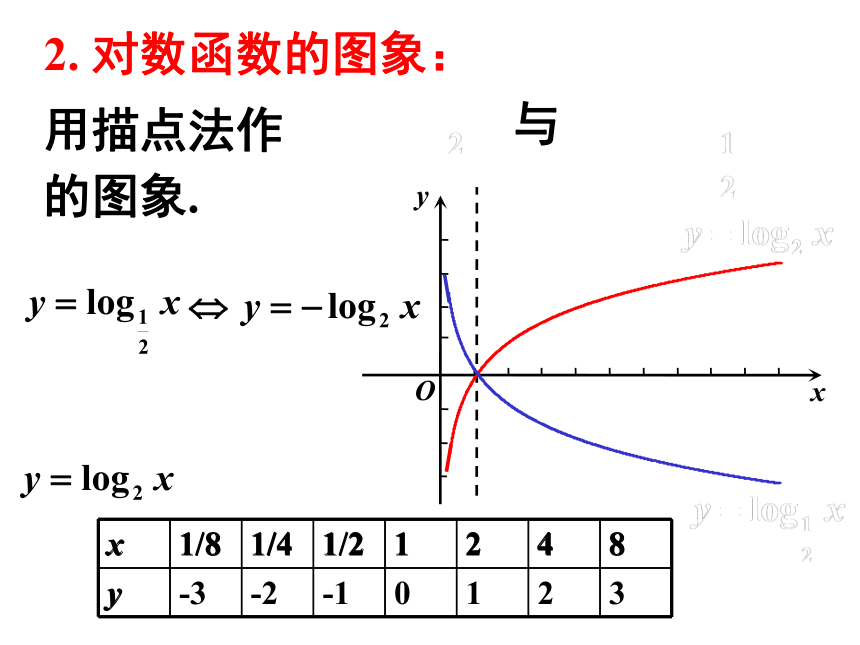
2. 对数函数的图象:
用描点法作
的图象.
与
x
y
O
x 1/8 1/4 1/2 1 2 4 8
y
x 1/8 1/4 1/2 1 2 4 8
y -3 -2 -1 0 1 2 3
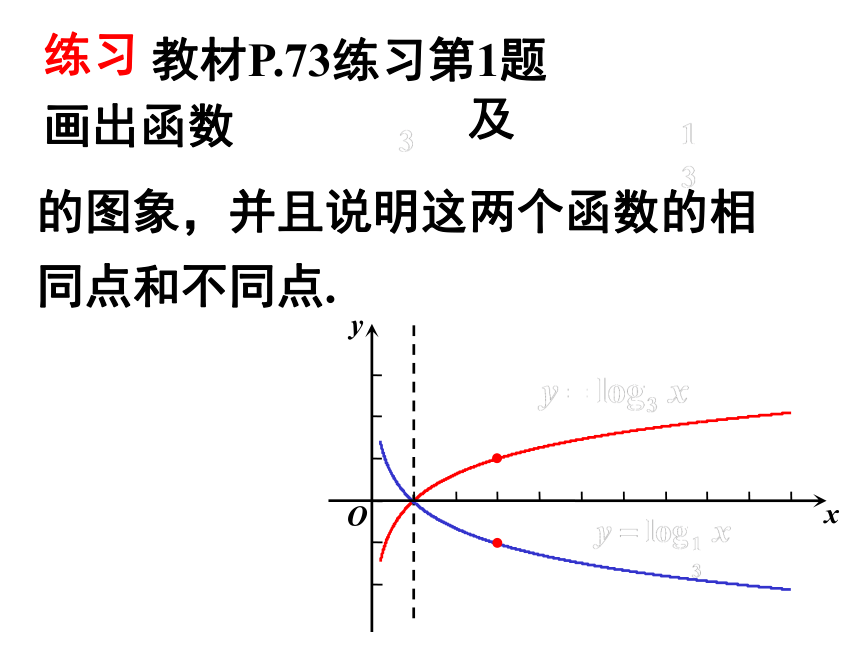
练习
教材P.73练习第1题
的图象,并且说明这两个函数的相
同点和不同点.
画出函数
及
x
y
O
x
y
O
3.对数函数的图象与性质
研究对数函数y=logax(a>0,且a≠1)的图象和性质时,底数要分为______与__________两种情况,如下表:
a>1
0<a<1
3. 对数函数的性质:
a>1 0<a<1
图 象
性 质
x
y
O
定义域:(0, +∞);
值域:R
过点(1, 0),即当x=1时,y=0.
在(0,+∞)上是减函数
在(0,+∞)上是增函数
x
y
O
1
1
x
y
O
性质(5):
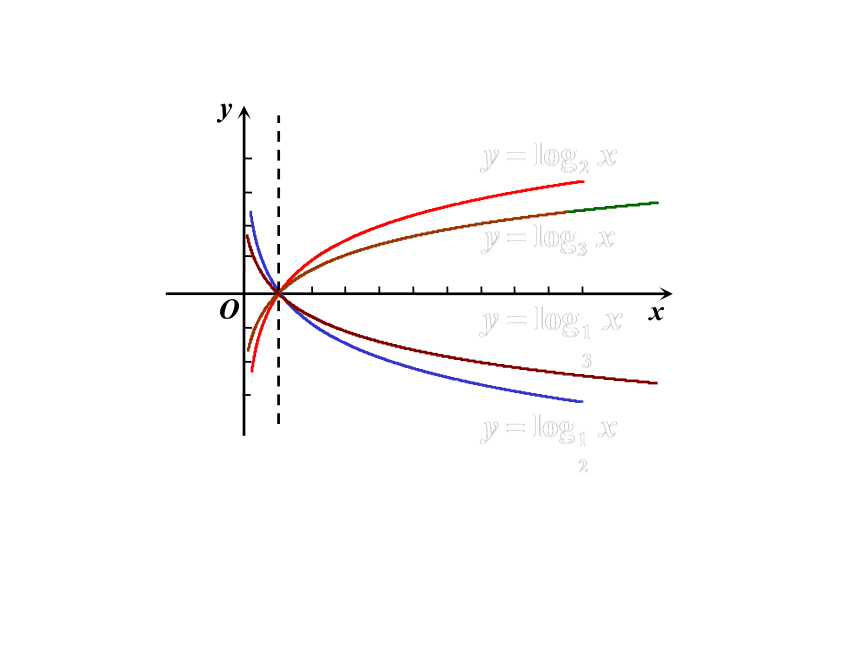
①上下比较:在直线x=1的右侧,a>1时,a越大,图象越靠近x轴;0②左右比较:(比较图象与y=1的交点)交点的横坐标越大,对应的对数函数的
底数越大.
解:
由
∴ 函数的定义域为
得
即
由
∴ 函数的定义域为 (1,2)∪(2,3) .
得
解:
解:
例3:
解:
法2:
∵ 3<3.5,2>1 ,
(4) ∵ 1.6<1.8,0<0.7<1,
例3:
2.2.2 对数函数及其性质(一)
问题: 某种细胞分裂时,由1个分裂为2个,2个分为4
个,……,一个这样的细胞分裂x次后,得到的细胞的
个数 y 与 x 的函数关系是:
现在我们来研究相反的问题.如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞,那么,分裂次数 x 就是要得到的细胞个数 y 的函数.
x=log2y
如果用x表示自变量,y表示函
数,这个函数就是 y=log2x.
1. 对数函数的定义:
函数 y=logax (a>0且a≠1)叫做
对数函数,其中x是自变量,函数的
定义域是
(0,+∞).
判断:下列函数是否为对数函数?
① y=logax2(a>0,且a≠1);
② y=log2x-1;
③ y=log2(x-1);
④ y=log5x;
⑤ y=logxa(x>0,且x≠1);
⑥ y=2log8x ;
⑦
【点拨】 一个函数为对数函数的条件是:
①系数为1;②底数为大于0且不等于1的常数;
③真数为单个自变量.
否
否
否
是
否
否
是
2. 对数函数的图象:
用描点法作
的图象.
与
x
y
O
x 1/8 1/4 1/2 1 2 4 8
y
x 1/8 1/4 1/2 1 2 4 8
y -3 -2 -1 0 1 2 3
练习
教材P.73练习第1题
的图象,并且说明这两个函数的相
同点和不同点.
画出函数
及
x
y
O
x
y
O
3.对数函数的图象与性质
研究对数函数y=logax(a>0,且a≠1)的图象和性质时,底数要分为______与__________两种情况,如下表:
a>1
0<a<1
3. 对数函数的性质:
a>1 0<a<1
图 象
性 质
x
y
O
定义域:(0, +∞);
值域:R
过点(1, 0),即当x=1时,y=0.
在(0,+∞)上是减函数
在(0,+∞)上是增函数
x
y
O
1
1
x
y
O
性质(5):
①上下比较:在直线x=1的右侧,a>1时,a越大,图象越靠近x轴;0
底数越大.
解:
由
∴ 函数的定义域为
得
即
由
∴ 函数的定义域为 (1,2)∪(2,3) .
得
解:
解:
例3:
解:
法2:
∵ 3<3.5,2>1 ,
(4) ∵ 1.6<1.8,0<0.7<1,
例3:
