6.3反比例函数的应用 同步测试2021-2022学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 6.3反比例函数的应用 同步测试2021-2022学年北师大版九年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 259.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 21:25:52 | ||
图片预览




文档简介
北师大版九年级数学上册第六章6.3反比例函数的应用 同步测试
一.选择题
1.如图,在平面直角坐标系中,直线y=x与反比例函数y=(x>0)的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交y轴于点B,交反比例函数图象于点C.若OA=2BC,则b的值为( )
A.1 B.2 C.3 D.4
2.面积是160平方米的长方形,它的长y米,宽x米之间的关系表达式是( )
A.y=160x B.y= C.y=160+x D.y=160﹣x
3.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )
体积x(mL) 100 80 60 40 20
压强y(kPa) 60 75 100 150 300
A.y=3000x B.y=6000x C.y= D.y=
4.如图,平行于y轴的直线分别交y=与y=的图象(部分)于点A、B,点C是y轴上的动点,则△ABC的面积为( )
A.k1﹣k2 B.(k1﹣k2) C.k2﹣k1 D.(k2﹣k1)
5.当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m2)的函数关系式为P=(S≠0),这个函数的图象大致是( )
A.B. C.D.
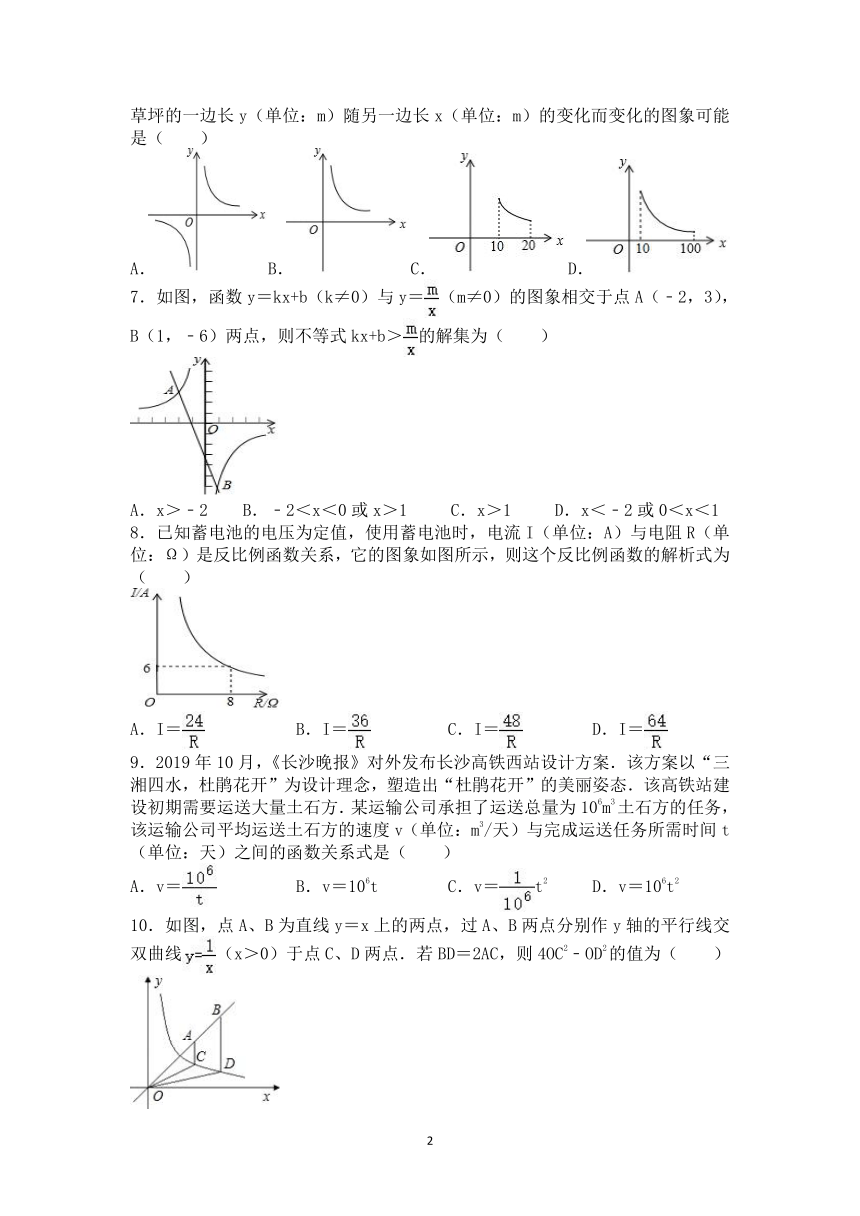
6.某学校要种植一块面积为200m2的长方形草坪,要求两边长均不小于10m,则草坪的一边长y(单位:m)随另一边长x(单位:m)的变化而变化的图象可能是( )
A.B.C.D.
7.如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为( )
A.x>﹣2 B.﹣2<x<0或x>1 C.x>1 D.x<﹣2或0<x<1
8.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则这个反比例函数的解析式为( )
A.I= B.I= C.I= D.I=
9.2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜鹃花开”为设计理念,塑造出“杜鹃花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为106m3土石方的任务,该运输公司平均运送土石方的速度v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数关系式是( )
A.v= B.v=106t C.v=t2 D.v=106t2
10.如图,点A、B为直线y=x上的两点,过A、B两点分别作y轴的平行线交双曲线(x>0)于点C、D两点.若BD=2AC,则4OC2﹣OD2的值为( )
A.5 B.6 C.7 D.8
二.填空题
11.有一面积为120的梯形,其上底是下底长的,若上底长为x,高为y,则y与x的函数关系式为____________ ;当高为10时,x=___________.
12.某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
年 度 2008 2009 2010 2011
投入技术改进资金x(万元) 2.5 3 4 4.5
产品成本y(万元∕件) 7.2 6 4.5 4
13. 如图,反比例函数(x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S矩形BDOE=4,则S△ACD=________.
14.某蓄水池的排水管的平均排水量为每小时8立方米,6小时可以将满池水全部排空.现在排水量为平均每小时Q立方米,那么将满池水排空所需要的时间为t(小时),写出时间t(小时)与Q之间的函数表达式 .
15.为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(分)的函数关系如图所示.已知药物燃烧阶段,y与x成正比例,燃烧完后,y与x成反比例.现测得药物10分钟燃烧完,此时教室内每立方米空气的含药量为8 mg.当每立方米空气中的含药量低于1.6 mg时,对人体才能无毒害作用.那么从消毒开始,经过________分钟后教室内的空气才能达到安全要求.
16.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)与体积v(单位:m3)满足函数关系式ρ=(k为常数,k≠0)其图象如图所示,则k的值为 .
17.如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比例函数y=的图象上,斜边OA1,A1A2,A2A3,…都在x轴上,则点A2的坐标是 .
18.如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=(k≠0)与△ABC有交点,则k的取值范围是 .
三.解答题
19.在大棚中栽培新品种的蘑菇,在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培,如图是某天恒温系统从开启升温到保持恒温及关闭.大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是函数y=(k>0)图象的一部分.
(1)分别求出0≤x≤2和x≥12时对应的y与x的函数关系式;
(2)若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间是多长?
20. 如图,一次函数y=x+1的图像交y轴于点A,与反比例函数(x>0)图像交于点B(m,2).
求反比例函数的表达式.
求△AOB的面积.
21.如图,一次函数y1=ax+b与反比例函数y2=的图象交于A、B两点.点A的横坐标为2,点B的纵坐标为1.
(1)求a,b的值.
(2)在反比例y2=第三象限的图象上找一点P,使点P到直线AB的距离最短,求点P的坐标.
22.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系.当R=4Ω时,I=9A.
(1)写出I关于R的函数解析式;
(2)完成下表,并在给定的平面直角坐标系中画出这个函数的图象;
R/Ω … …
I/A … …
(3)如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围内?
23.某地上年度电价为0.8元/度,年用电量为1亿度,本年度计划将电价调至0.55~0.75元/度之间,经测算,若电价调至x元/度,则本年度新增用电量y(亿度)与(x-0.4)成反比例.又知当x=0.65时,y=0.8.
(1)求y与x之间的函数解析式;
(2)若每度电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年度增加20%?[收益=用电量×(实际电价-成本价)]
24.某环保行活动拒绝污染正式开启,由于长期采磷及磷化工发展造成了总磷污染.当地政府提出五条整改措施,力求在60天以内使总磷含量达标(即总磷浓度低于0.2mg/L).整改过程中,总磷浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前5天的变化规律,且线段AB所在直线的表达式为:y=﹣x+4,从第5天起,该支流总磷浓度y与时间x成反比例关系.
(1)求整改全过程中总磷浓度y与时间x的函数表达式;
(2)该支流中总磷的浓度能否在60天以内达标?说明理由.
答案提示
1.C.2.B.3.D.4.B.5.C.6.C.7.D.8.C.9.A.
10.解:延长AC交x轴于E,延长BD交x轴于F.
设A、B的横坐标分别是a,b,
∵点A、B为直线y=x上的两点,
∴A的坐标是(a,a),B的坐标是(b,b).则AE=OE=a,BF=OF=b.
∵C、D两点在交双曲线(x>0)上,则CE=,DF=.
∴BD=BF﹣DF=b﹣,AC=a﹣.
又∵BD=2AC
∴b﹣=2(a﹣),
两边平方得:b2+﹣2=4(a2+﹣2),即b2+=4(a2+)﹣6.
在直角△OCE中,OC2=OE2+CE2=a2+,同理OD2=b2+,
∴4OC2﹣0D2=4(a2+)﹣(b2+)=6.
故选:B.
11.y=, 9.6 12.y=. 13. 14.t=. 15.50. 16.9.
17.解:如图,过点P1作P1M⊥x轴于M,
∵△OAP1是等腰直角三角形,
∴P1M=OM,
∴设P1点的坐标是(a,a),
把(a,a)代入解析式得到a=2,
∴P1的坐标是(2,2),
则OA1=4,
∵△P2A1A2是等腰直角三角形,过点P2作P2N⊥x轴于N,
设P2的纵坐标是b,
∴横坐标是b+4,
把P2的坐标代入解析式y=,
∴b+4=,
∴b=2﹣2,
∴点P2的横坐标为2+2,
∴P2点的坐标是(2+2,2﹣2),
∴点A2的坐标是(4,0).
故答案为:(4,0).
18.解:如图,设直线y=x与BC交于E点,分别过A、E两点作x轴的垂线,垂足为D、F,EF交AB于M,
∵A点的横坐标为1,A点在直线y=x上,
∴A(1,1),
又∵AB=AC=2,AB∥x轴,AC∥y轴,
∴B(3,1),C(1,3),且△ABC为等腰直角三角形,
BC的中点坐标为(,),即为(2,2),
∵点(2,2)满足直线y=x,
∴点(2,2)即为E点坐标,E点坐标为(2,2),
∴k=OD×AD=1,或k=OF×EF=4,
当双曲线与△ABC有唯一交点时,1≤k≤4.
故答案为:1≤k≤4.
19.解:(1)设AD的解析式为:y=kx+b(0≤x≤2),
把A(2,18)和D(0,10)代入得:,
解得:,
∴0≤x≤2时,y=4x+10;
把B(12,18)代入函数y=(k>0)中得:k=12×18=216,
∴;
(2)当4x+10=12,x=0.5,
当,x=18,
18﹣0.5=17.5,
答:这天该种蘑菇适宜生长的时间17.5小时.
20.解:(1)∵一次函数经过点B,
∴2=m+1
解得m=1,则点B的坐标为(1,2)
又∵点B过y=. 解得k=2,
即反比例函数为y= .
(2)∵点A(0,1)∴OA=1,
过点B作BC⊥y轴,垂足为点C ,
则BC就是△AOB的高,BC=1,
∴S△AOB =OA×BC=×1×1=.
21.解:(1)∵一次函数y1=ax+b与反比例函数y2=的图象交于A、B两点.点A的横坐标为2,点B的纵坐标为1,
∴A(2,2),B(4,1),
则有,
解得.
(2)过点P作直线PM∥AB,
当直线PM与反比例函数只有一个交点时,点P到直线AB的距离最短,
设直线PM的解析式为y=﹣x+n,
由,消去y得到,x2﹣2nx+8=0,
由题意得,△=0,
∴4n2﹣32=0,
∴n=﹣2或2(舍弃),
解得,
∴P(﹣2,﹣).
22.解:(1)电流I是电阻R的反比例函数,设I=,
∵R=4Ω时,I=9A
∴9=,
解得k=4×9=36,
∴I=(R>0);
(2)列表如下:
R/Ω … 3 4 5 6 8 9 10 12 …
I/A … 12 9 7.2 6 4.5 4 3.6 3 …
(3)∵I≤10,I=,
∴≤10,
∴R≥3.6,
即用电器可变电阻应控制在不低于3.6欧的范围内.
23.解:(1)∵本年度新增用电量y(亿度)与(x-0.4)成反比例关系,
∴设y=(k为常数,且k≠0).
∵当电价为0.65元/度时,新增用电量是0.8亿度,
∴0.8=,
解得k=0.2,
∴y==.
(2)设当电价调至x元/度时,本年度电力部门的收益将比上年度增加20%.
根据题意,得(0.8-0.3)×1×(1+20%)=(+1)(x-0.3),
解得x=0.6或x=0.5(舍去).
故若每度电的成本价为0.3元,则当电价调至0.6元/度时,本年度电力部门的收益将比上年度增加20%.
24.解:(1)分情况讨论:
当x>5时,设y=,把(5,2)代入得:m=10,
所以y=;
当0≤x≤5时,y=﹣x+4,
所以整改全过程中总磷浓度y与时间x的函数表达式为:
y=;
(2)能,理由如下:
当y=0.2时,有=0.2,则x=50<60,
故该支流中总磷的浓度能在60天以内达标.
一.选择题
1.如图,在平面直角坐标系中,直线y=x与反比例函数y=(x>0)的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交y轴于点B,交反比例函数图象于点C.若OA=2BC,则b的值为( )
A.1 B.2 C.3 D.4
2.面积是160平方米的长方形,它的长y米,宽x米之间的关系表达式是( )
A.y=160x B.y= C.y=160+x D.y=160﹣x
3.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )
体积x(mL) 100 80 60 40 20
压强y(kPa) 60 75 100 150 300
A.y=3000x B.y=6000x C.y= D.y=
4.如图,平行于y轴的直线分别交y=与y=的图象(部分)于点A、B,点C是y轴上的动点,则△ABC的面积为( )
A.k1﹣k2 B.(k1﹣k2) C.k2﹣k1 D.(k2﹣k1)
5.当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m2)的函数关系式为P=(S≠0),这个函数的图象大致是( )
A.B. C.D.
6.某学校要种植一块面积为200m2的长方形草坪,要求两边长均不小于10m,则草坪的一边长y(单位:m)随另一边长x(单位:m)的变化而变化的图象可能是( )
A.B.C.D.
7.如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为( )
A.x>﹣2 B.﹣2<x<0或x>1 C.x>1 D.x<﹣2或0<x<1
8.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则这个反比例函数的解析式为( )
A.I= B.I= C.I= D.I=
9.2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜鹃花开”为设计理念,塑造出“杜鹃花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为106m3土石方的任务,该运输公司平均运送土石方的速度v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数关系式是( )
A.v= B.v=106t C.v=t2 D.v=106t2
10.如图,点A、B为直线y=x上的两点,过A、B两点分别作y轴的平行线交双曲线(x>0)于点C、D两点.若BD=2AC,则4OC2﹣OD2的值为( )
A.5 B.6 C.7 D.8
二.填空题
11.有一面积为120的梯形,其上底是下底长的,若上底长为x,高为y,则y与x的函数关系式为____________ ;当高为10时,x=___________.
12.某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
年 度 2008 2009 2010 2011
投入技术改进资金x(万元) 2.5 3 4 4.5
产品成本y(万元∕件) 7.2 6 4.5 4
13. 如图,反比例函数(x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S矩形BDOE=4,则S△ACD=________.
14.某蓄水池的排水管的平均排水量为每小时8立方米,6小时可以将满池水全部排空.现在排水量为平均每小时Q立方米,那么将满池水排空所需要的时间为t(小时),写出时间t(小时)与Q之间的函数表达式 .
15.为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(分)的函数关系如图所示.已知药物燃烧阶段,y与x成正比例,燃烧完后,y与x成反比例.现测得药物10分钟燃烧完,此时教室内每立方米空气的含药量为8 mg.当每立方米空气中的含药量低于1.6 mg时,对人体才能无毒害作用.那么从消毒开始,经过________分钟后教室内的空气才能达到安全要求.
16.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)与体积v(单位:m3)满足函数关系式ρ=(k为常数,k≠0)其图象如图所示,则k的值为 .
17.如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比例函数y=的图象上,斜边OA1,A1A2,A2A3,…都在x轴上,则点A2的坐标是 .
18.如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=(k≠0)与△ABC有交点,则k的取值范围是 .
三.解答题
19.在大棚中栽培新品种的蘑菇,在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培,如图是某天恒温系统从开启升温到保持恒温及关闭.大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是函数y=(k>0)图象的一部分.
(1)分别求出0≤x≤2和x≥12时对应的y与x的函数关系式;
(2)若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间是多长?
20. 如图,一次函数y=x+1的图像交y轴于点A,与反比例函数(x>0)图像交于点B(m,2).
求反比例函数的表达式.
求△AOB的面积.
21.如图,一次函数y1=ax+b与反比例函数y2=的图象交于A、B两点.点A的横坐标为2,点B的纵坐标为1.
(1)求a,b的值.
(2)在反比例y2=第三象限的图象上找一点P,使点P到直线AB的距离最短,求点P的坐标.
22.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系.当R=4Ω时,I=9A.
(1)写出I关于R的函数解析式;
(2)完成下表,并在给定的平面直角坐标系中画出这个函数的图象;
R/Ω … …
I/A … …
(3)如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围内?
23.某地上年度电价为0.8元/度,年用电量为1亿度,本年度计划将电价调至0.55~0.75元/度之间,经测算,若电价调至x元/度,则本年度新增用电量y(亿度)与(x-0.4)成反比例.又知当x=0.65时,y=0.8.
(1)求y与x之间的函数解析式;
(2)若每度电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年度增加20%?[收益=用电量×(实际电价-成本价)]
24.某环保行活动拒绝污染正式开启,由于长期采磷及磷化工发展造成了总磷污染.当地政府提出五条整改措施,力求在60天以内使总磷含量达标(即总磷浓度低于0.2mg/L).整改过程中,总磷浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前5天的变化规律,且线段AB所在直线的表达式为:y=﹣x+4,从第5天起,该支流总磷浓度y与时间x成反比例关系.
(1)求整改全过程中总磷浓度y与时间x的函数表达式;
(2)该支流中总磷的浓度能否在60天以内达标?说明理由.
答案提示
1.C.2.B.3.D.4.B.5.C.6.C.7.D.8.C.9.A.
10.解:延长AC交x轴于E,延长BD交x轴于F.
设A、B的横坐标分别是a,b,
∵点A、B为直线y=x上的两点,
∴A的坐标是(a,a),B的坐标是(b,b).则AE=OE=a,BF=OF=b.
∵C、D两点在交双曲线(x>0)上,则CE=,DF=.
∴BD=BF﹣DF=b﹣,AC=a﹣.
又∵BD=2AC
∴b﹣=2(a﹣),
两边平方得:b2+﹣2=4(a2+﹣2),即b2+=4(a2+)﹣6.
在直角△OCE中,OC2=OE2+CE2=a2+,同理OD2=b2+,
∴4OC2﹣0D2=4(a2+)﹣(b2+)=6.
故选:B.
11.y=, 9.6 12.y=. 13. 14.t=. 15.50. 16.9.
17.解:如图,过点P1作P1M⊥x轴于M,
∵△OAP1是等腰直角三角形,
∴P1M=OM,
∴设P1点的坐标是(a,a),
把(a,a)代入解析式得到a=2,
∴P1的坐标是(2,2),
则OA1=4,
∵△P2A1A2是等腰直角三角形,过点P2作P2N⊥x轴于N,
设P2的纵坐标是b,
∴横坐标是b+4,
把P2的坐标代入解析式y=,
∴b+4=,
∴b=2﹣2,
∴点P2的横坐标为2+2,
∴P2点的坐标是(2+2,2﹣2),
∴点A2的坐标是(4,0).
故答案为:(4,0).
18.解:如图,设直线y=x与BC交于E点,分别过A、E两点作x轴的垂线,垂足为D、F,EF交AB于M,
∵A点的横坐标为1,A点在直线y=x上,
∴A(1,1),
又∵AB=AC=2,AB∥x轴,AC∥y轴,
∴B(3,1),C(1,3),且△ABC为等腰直角三角形,
BC的中点坐标为(,),即为(2,2),
∵点(2,2)满足直线y=x,
∴点(2,2)即为E点坐标,E点坐标为(2,2),
∴k=OD×AD=1,或k=OF×EF=4,
当双曲线与△ABC有唯一交点时,1≤k≤4.
故答案为:1≤k≤4.
19.解:(1)设AD的解析式为:y=kx+b(0≤x≤2),
把A(2,18)和D(0,10)代入得:,
解得:,
∴0≤x≤2时,y=4x+10;
把B(12,18)代入函数y=(k>0)中得:k=12×18=216,
∴;
(2)当4x+10=12,x=0.5,
当,x=18,
18﹣0.5=17.5,
答:这天该种蘑菇适宜生长的时间17.5小时.
20.解:(1)∵一次函数经过点B,
∴2=m+1
解得m=1,则点B的坐标为(1,2)
又∵点B过y=. 解得k=2,
即反比例函数为y= .
(2)∵点A(0,1)∴OA=1,
过点B作BC⊥y轴,垂足为点C ,
则BC就是△AOB的高,BC=1,
∴S△AOB =OA×BC=×1×1=.
21.解:(1)∵一次函数y1=ax+b与反比例函数y2=的图象交于A、B两点.点A的横坐标为2,点B的纵坐标为1,
∴A(2,2),B(4,1),
则有,
解得.
(2)过点P作直线PM∥AB,
当直线PM与反比例函数只有一个交点时,点P到直线AB的距离最短,
设直线PM的解析式为y=﹣x+n,
由,消去y得到,x2﹣2nx+8=0,
由题意得,△=0,
∴4n2﹣32=0,
∴n=﹣2或2(舍弃),
解得,
∴P(﹣2,﹣).
22.解:(1)电流I是电阻R的反比例函数,设I=,
∵R=4Ω时,I=9A
∴9=,
解得k=4×9=36,
∴I=(R>0);
(2)列表如下:
R/Ω … 3 4 5 6 8 9 10 12 …
I/A … 12 9 7.2 6 4.5 4 3.6 3 …
(3)∵I≤10,I=,
∴≤10,
∴R≥3.6,
即用电器可变电阻应控制在不低于3.6欧的范围内.
23.解:(1)∵本年度新增用电量y(亿度)与(x-0.4)成反比例关系,
∴设y=(k为常数,且k≠0).
∵当电价为0.65元/度时,新增用电量是0.8亿度,
∴0.8=,
解得k=0.2,
∴y==.
(2)设当电价调至x元/度时,本年度电力部门的收益将比上年度增加20%.
根据题意,得(0.8-0.3)×1×(1+20%)=(+1)(x-0.3),
解得x=0.6或x=0.5(舍去).
故若每度电的成本价为0.3元,则当电价调至0.6元/度时,本年度电力部门的收益将比上年度增加20%.
24.解:(1)分情况讨论:
当x>5时,设y=,把(5,2)代入得:m=10,
所以y=;
当0≤x≤5时,y=﹣x+4,
所以整改全过程中总磷浓度y与时间x的函数表达式为:
y=;
(2)能,理由如下:
当y=0.2时,有=0.2,则x=50<60,
故该支流中总磷的浓度能在60天以内达标.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
