6.2反比例函数的图形和性质 同步测试2021-2022学年北师大版九年级数学上册(Word版含答案)
文档属性
| 名称 | 6.2反比例函数的图形和性质 同步测试2021-2022学年北师大版九年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 267.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 21:29:58 | ||
图片预览




文档简介
北师大版九年级数学上册第六章
6.2反比例函数的图形和性质 同步测试
一.选择题
1.下列函数中,当x>0时,函数值y随x的增大而减小的是( )
A.y= B.y= C.y= D.y=﹣
2.反比例函数图象经过点(2,3),则n的值是( )
A.-2 B.-1 C.0 D.1
3.在同一直角坐标系中,一次函数y=kx-k与反比例函数(k≠0)的图象大致是( )
A. B. C. D.
4.如果点A(-1,)、B(1,)、C(2,)是反比例函数图象上的三个点,则下列结论正确的是( )
A.>> B.>> C.>> D.>>
5.如图所示,y=mx+m与y=(m<0)在同一坐标系中的图象可能是图中的( )
A.B.C.D.
6.若函数是反比例函数,且图象在第一,三象限,那么m的值是( )
A.±1 B.1 C.-1 D.2
7.如图,点P(﹣2a,a)是反比例函数y=与⊙O的一个交点,图中阴影部分的面积为10π,则该反比例函数的表达式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=﹣
8.反比例函数的图象如图所示,则k的值可能是( )
A.-1 B.1 C.2 D.
9.已知点 A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=(k<0)的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y3<y1<y2
10.如图所示,菱形ABCD的顶点A、C在x轴上,反比例函数y=经过点D和BC中点E,若菱形ABCD的面积是16,则k的值为( )
A.﹣1 B.﹣ C.﹣ D.﹣2
二.填空题
11.反比例函数经过(﹣3,2),则图象在 象限.
12.已知点P(1,2)在反比例函数的图象上,根据图象判断,当x>1时,y的取值范围是
13.若函数y=的图象在其所在的每一个象限内,函数值y随自变量x的增大而增大,则m的取值范围是 .
14.反比例函数的图象在第一、三象限,则m的取值范围是 .
15.如图,是反比例函数和(<)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若,则的值为
16.如图,点A在双曲线y=上,点B在双曲线y=(k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是9,则k的值为 .
17.已知点A(2,3)在反比例函数y=(k≠0)的图象上,当x>﹣2时,则y的取值范围是 .
18.如图,已知点A在反比例函数图象上,AC⊥y轴于点C,点B在x轴的负半轴上,且△ABC的面积为3,则该反比例函数的表达式为 .
三.解答题
19.某班数学兴趣小组根据学习函数的经验,通过列表、描点、连线的方法对函数y=的图象与性质进行了研究,研究过程如下,请补充完整.
(1)y与x的几组对应值如下表:
x … ﹣3 ﹣2 ﹣1 1 2 3 …
y … 6 6 m …
函数y=的自变量x的取值范围是 x≠0 ,m的值为 ;
(2)在给出的平面直角坐标系中,描出以上表中各组对应值为坐标的点,画出函数y=的大致图象,并写出该函数的两条性质;
(3)在同一坐标系中画出函数y1=x的图象,并根据图象直接写出当y>y1时,自变量x的取值范围.
20.如图,正方形ABOC的边长为2,反比例函数过点A,求k的值.
21.已知反比例函数y=的图象经过点A(2,﹣4).
(1)求k的值;
(2)函数的图象在哪几个象限?y随x的增大怎样变化?
(3)画出函数的图象;
(4)点B(,﹣16)、C(﹣3,5)在这个函数的图象上吗?
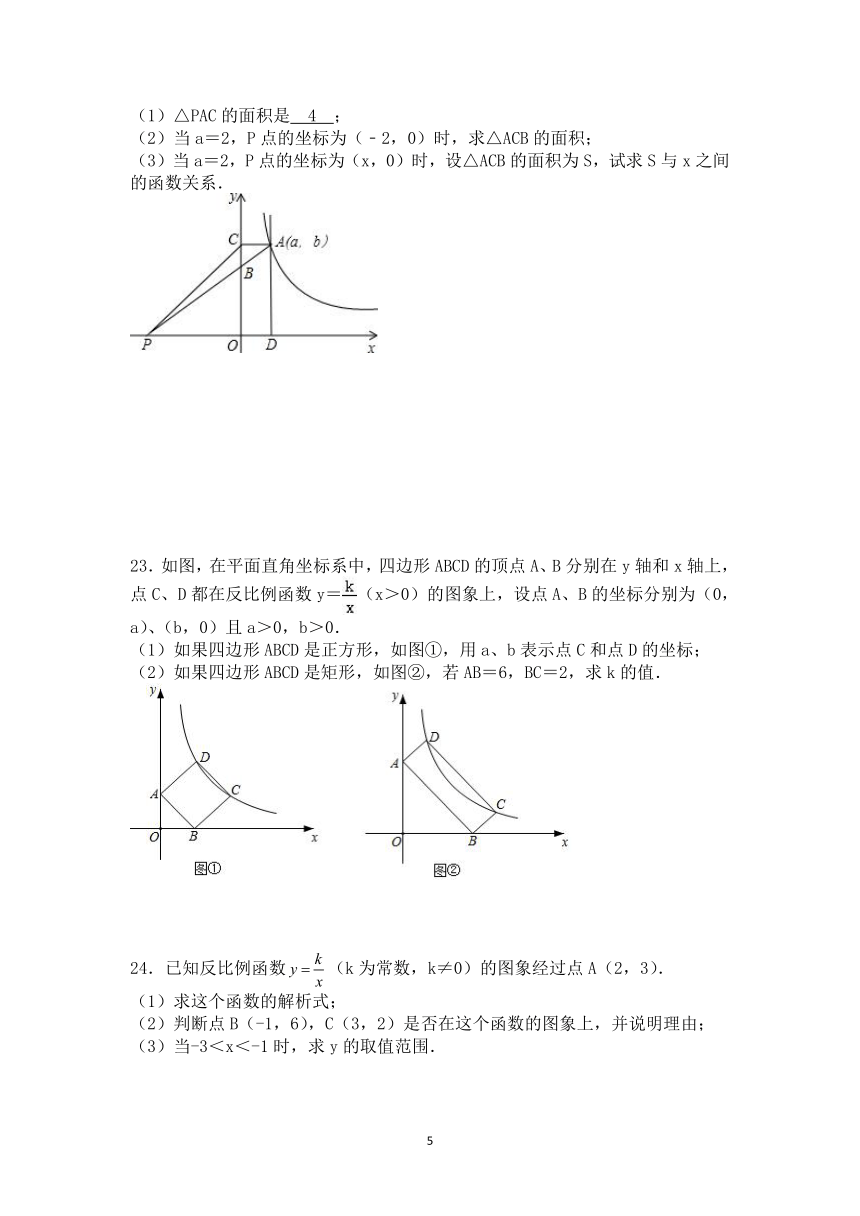
22.如图,点A(a,b)是双曲线y=(x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于C点,过A作AD⊥x轴于D点,连接AP交y轴于B点.
(1)△PAC的面积是 4 ;
(2)当a=2,P点的坐标为(﹣2,0)时,求△ACB的面积;
(3)当a=2,P点的坐标为(x,0)时,设△ACB的面积为S,试求S与x之间的函数关系.
23.如图,在平面直角坐标系中,四边形ABCD的顶点A、B分别在y轴和x轴上,点C、D都在反比例函数y=(x>0)的图象上,设点A、B的坐标分别为(0,a)、(b,0)且a>0,b>0.
(1)如果四边形ABCD是正方形,如图①,用a、b表示点C和点D的坐标;
(2)如果四边形ABCD是矩形,如图②,若AB=6,BC=2,求k的值.
24.已知反比例函数(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D,M分别在边AB,OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
答案提示
1.A.2.D.3.A.4.A.5.D.6.C.7.D.8.D.9.D.
10.解:连接BD交AC于点F,连接EF,OE,过点E作EG⊥AC,垂足为G,
∵ABCD是菱形,
∴S△BFC=S菱形=4,
∵点E是BC的中点,
∴S△FEC=S△FEB=S△FBC=2,
∴S△FEG=S△GEC=S△FEC=1,
∵反比例函数y=的图象经过点D和点E,
∴OF DF=OG EG=|k|,
∵EG=DF,
∴OG=2OF,
∴S△OGE=2S△OFE,即,S△OGE=S△FGE=×1=,
∴|k|=,
∴k=(舍去),或k=﹣,
故选:C.
11.二 四. 12.0<y<2. 13.m<﹣2. 14.m>1.
15.4. 16.13. 17.y<﹣3或y>0. 18.y=﹣.
19.解:(1)函数y=的自变量x的取值范围是x≠0,当x=2时,m==;
故答案为:x≠0;;
(2)函数y=的图象如图所示,性质:①该函数图象关于y轴对称;②当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小;
(3)在同一坐标系中画出函数y1=x的图象如图所示;当y>y1时,自变量x的取值范围为x<0或0<x<2.
20.解:根据题意,知
|k|==4,k=±4,
又∵k<0,
∴k=-4.
21.解:(1)∵反比例函数y= 的图象经过点A(2,﹣4),
∴k=2×(﹣4)=﹣8;
(2)∵k=﹣8<0,
∴图象位于二、四象限,在每个象限内y随x的增大而增大;
(3)图象为:
(4)∵×(﹣16)=﹣8、
﹣3×5=﹣15≠﹣8,
∴B(,﹣16)在反比例函数的图象上,C(﹣3,5)不在反比例函数的图象上.
22.解:(1)∵点A(a,b)是双曲线y=(x>0)上,
∴ab=8,
∵AC⊥y轴于C点,AD⊥x轴于D点,
∴AC=a,AD=b,
∴△PAC的面积=AD AC=ab=4;
故答案为:4;
(2)∵a=2,
∴b=4,
∴AC=2,AD=4,A(2,4),
设直线AP的解析式为y=kx+b,
∴,
∴,
∴直线AP的解析式为y=x+2,
∴B(0,2),
∴S△ABC=AC BC==2;
(3)同理直线AP的解析式为y=﹣,
∴B(0,﹣),
∴BC=4+=
∴S=×2×=.
23.解:(1)如图1,过点C作CM⊥x轴,垂足为M,过点D作DN⊥y轴,垂足为N,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠DAB=90°,
∵∠ABO+∠BAO=90°,∠ABO+∠CBM=90°,
∴∠BAO=∠CBM,
∴△AOB≌△BMC (AAS),
∴OA=BM=a,OB=MC=b,
∴点C(a+b,b),
同理,D(a,a+b);
(2)如图2,由(1)的方法可得,△AOB∽△BMC,
∴====,
∴BM=OA=a,CM=b,
∴点C(b+a,b),
同理,点D(a,a+b),
∵点C、D在反比例函数的图象上,
∴(b+a)×b=a×(a+b),
∴a=b,
在Rt△AOB中,a=b=AB=3,
∴k=(b+a)×b=8,
答:k的值为8.
24.解:(1)∵反比例函数(k为常数,k≠0)的图象经过点A(2,3),
∴把点A的坐标代入解析式,得,
解得,k=6,
∴这个函数的解析式为:;
(2)∵反比例函数解析式,
∴6=xy.
分别把点B、C的坐标代入,得
(-1)×6=-6≠6,则点B不在该函数图象上.
3×2=6,则点C在该函数图象上;
(3)∵当x=-3时,y=-2,当x=-1时,y=-6,
又∵k>0,
∴当x<0时,y随x的增大而减小,
∴当-3<x<-1时,-6<y<-2.
(1)∵正方形OABC的顶点C(0,3),
∴OA=AB=BC=OC=3,∠OAB=∠B=∠BCO=90°,
∵AD=2DB,∴AD=AB=2,∴D(-3,2).
把D点坐标代入y=,得m=-6,
∴反比例函数的表达式为y=-,
∵AM=2MO,∴MO=OA=1,即M(-1,0),
把点M与点D的坐标代入y=kx+b中,得
解得
则一次函数的表达式为y=-x-1.(2)把y=3代入y=-,得x=-2,∴N(-2,3),即NC=2,设P(x,y),
∵△OPM的面积与四边形OMNC的面积相等,
∴OM|y|=(OM+NC)·OC,即|y|=9,解得y=±9,
当y=9时,x=-10,
当y=-9时,x=8,
则点P的坐标为(-10,9)或(8,-9).
6.2反比例函数的图形和性质 同步测试
一.选择题
1.下列函数中,当x>0时,函数值y随x的增大而减小的是( )
A.y= B.y= C.y= D.y=﹣
2.反比例函数图象经过点(2,3),则n的值是( )
A.-2 B.-1 C.0 D.1
3.在同一直角坐标系中,一次函数y=kx-k与反比例函数(k≠0)的图象大致是( )
A. B. C. D.
4.如果点A(-1,)、B(1,)、C(2,)是反比例函数图象上的三个点,则下列结论正确的是( )
A.>> B.>> C.>> D.>>
5.如图所示,y=mx+m与y=(m<0)在同一坐标系中的图象可能是图中的( )
A.B.C.D.
6.若函数是反比例函数,且图象在第一,三象限,那么m的值是( )
A.±1 B.1 C.-1 D.2
7.如图,点P(﹣2a,a)是反比例函数y=与⊙O的一个交点,图中阴影部分的面积为10π,则该反比例函数的表达式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=﹣
8.反比例函数的图象如图所示,则k的值可能是( )
A.-1 B.1 C.2 D.
9.已知点 A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=(k<0)的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y3<y1<y2
10.如图所示,菱形ABCD的顶点A、C在x轴上,反比例函数y=经过点D和BC中点E,若菱形ABCD的面积是16,则k的值为( )
A.﹣1 B.﹣ C.﹣ D.﹣2
二.填空题
11.反比例函数经过(﹣3,2),则图象在 象限.
12.已知点P(1,2)在反比例函数的图象上,根据图象判断,当x>1时,y的取值范围是
13.若函数y=的图象在其所在的每一个象限内,函数值y随自变量x的增大而增大,则m的取值范围是 .
14.反比例函数的图象在第一、三象限,则m的取值范围是 .
15.如图,是反比例函数和(<)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若,则的值为
16.如图,点A在双曲线y=上,点B在双曲线y=(k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是9,则k的值为 .
17.已知点A(2,3)在反比例函数y=(k≠0)的图象上,当x>﹣2时,则y的取值范围是 .
18.如图,已知点A在反比例函数图象上,AC⊥y轴于点C,点B在x轴的负半轴上,且△ABC的面积为3,则该反比例函数的表达式为 .
三.解答题
19.某班数学兴趣小组根据学习函数的经验,通过列表、描点、连线的方法对函数y=的图象与性质进行了研究,研究过程如下,请补充完整.
(1)y与x的几组对应值如下表:
x … ﹣3 ﹣2 ﹣1 1 2 3 …
y … 6 6 m …
函数y=的自变量x的取值范围是 x≠0 ,m的值为 ;
(2)在给出的平面直角坐标系中,描出以上表中各组对应值为坐标的点,画出函数y=的大致图象,并写出该函数的两条性质;
(3)在同一坐标系中画出函数y1=x的图象,并根据图象直接写出当y>y1时,自变量x的取值范围.
20.如图,正方形ABOC的边长为2,反比例函数过点A,求k的值.
21.已知反比例函数y=的图象经过点A(2,﹣4).
(1)求k的值;
(2)函数的图象在哪几个象限?y随x的增大怎样变化?
(3)画出函数的图象;
(4)点B(,﹣16)、C(﹣3,5)在这个函数的图象上吗?
22.如图,点A(a,b)是双曲线y=(x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于C点,过A作AD⊥x轴于D点,连接AP交y轴于B点.
(1)△PAC的面积是 4 ;
(2)当a=2,P点的坐标为(﹣2,0)时,求△ACB的面积;
(3)当a=2,P点的坐标为(x,0)时,设△ACB的面积为S,试求S与x之间的函数关系.
23.如图,在平面直角坐标系中,四边形ABCD的顶点A、B分别在y轴和x轴上,点C、D都在反比例函数y=(x>0)的图象上,设点A、B的坐标分别为(0,a)、(b,0)且a>0,b>0.
(1)如果四边形ABCD是正方形,如图①,用a、b表示点C和点D的坐标;
(2)如果四边形ABCD是矩形,如图②,若AB=6,BC=2,求k的值.
24.已知反比例函数(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D,M分别在边AB,OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
答案提示
1.A.2.D.3.A.4.A.5.D.6.C.7.D.8.D.9.D.
10.解:连接BD交AC于点F,连接EF,OE,过点E作EG⊥AC,垂足为G,
∵ABCD是菱形,
∴S△BFC=S菱形=4,
∵点E是BC的中点,
∴S△FEC=S△FEB=S△FBC=2,
∴S△FEG=S△GEC=S△FEC=1,
∵反比例函数y=的图象经过点D和点E,
∴OF DF=OG EG=|k|,
∵EG=DF,
∴OG=2OF,
∴S△OGE=2S△OFE,即,S△OGE=S△FGE=×1=,
∴|k|=,
∴k=(舍去),或k=﹣,
故选:C.
11.二 四. 12.0<y<2. 13.m<﹣2. 14.m>1.
15.4. 16.13. 17.y<﹣3或y>0. 18.y=﹣.
19.解:(1)函数y=的自变量x的取值范围是x≠0,当x=2时,m==;
故答案为:x≠0;;
(2)函数y=的图象如图所示,性质:①该函数图象关于y轴对称;②当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小;
(3)在同一坐标系中画出函数y1=x的图象如图所示;当y>y1时,自变量x的取值范围为x<0或0<x<2.
20.解:根据题意,知
|k|==4,k=±4,
又∵k<0,
∴k=-4.
21.解:(1)∵反比例函数y= 的图象经过点A(2,﹣4),
∴k=2×(﹣4)=﹣8;
(2)∵k=﹣8<0,
∴图象位于二、四象限,在每个象限内y随x的增大而增大;
(3)图象为:
(4)∵×(﹣16)=﹣8、
﹣3×5=﹣15≠﹣8,
∴B(,﹣16)在反比例函数的图象上,C(﹣3,5)不在反比例函数的图象上.
22.解:(1)∵点A(a,b)是双曲线y=(x>0)上,
∴ab=8,
∵AC⊥y轴于C点,AD⊥x轴于D点,
∴AC=a,AD=b,
∴△PAC的面积=AD AC=ab=4;
故答案为:4;
(2)∵a=2,
∴b=4,
∴AC=2,AD=4,A(2,4),
设直线AP的解析式为y=kx+b,
∴,
∴,
∴直线AP的解析式为y=x+2,
∴B(0,2),
∴S△ABC=AC BC==2;
(3)同理直线AP的解析式为y=﹣,
∴B(0,﹣),
∴BC=4+=
∴S=×2×=.
23.解:(1)如图1,过点C作CM⊥x轴,垂足为M,过点D作DN⊥y轴,垂足为N,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠DAB=90°,
∵∠ABO+∠BAO=90°,∠ABO+∠CBM=90°,
∴∠BAO=∠CBM,
∴△AOB≌△BMC (AAS),
∴OA=BM=a,OB=MC=b,
∴点C(a+b,b),
同理,D(a,a+b);
(2)如图2,由(1)的方法可得,△AOB∽△BMC,
∴====,
∴BM=OA=a,CM=b,
∴点C(b+a,b),
同理,点D(a,a+b),
∵点C、D在反比例函数的图象上,
∴(b+a)×b=a×(a+b),
∴a=b,
在Rt△AOB中,a=b=AB=3,
∴k=(b+a)×b=8,
答:k的值为8.
24.解:(1)∵反比例函数(k为常数,k≠0)的图象经过点A(2,3),
∴把点A的坐标代入解析式,得,
解得,k=6,
∴这个函数的解析式为:;
(2)∵反比例函数解析式,
∴6=xy.
分别把点B、C的坐标代入,得
(-1)×6=-6≠6,则点B不在该函数图象上.
3×2=6,则点C在该函数图象上;
(3)∵当x=-3时,y=-2,当x=-1时,y=-6,
又∵k>0,
∴当x<0时,y随x的增大而减小,
∴当-3<x<-1时,-6<y<-2.
(1)∵正方形OABC的顶点C(0,3),
∴OA=AB=BC=OC=3,∠OAB=∠B=∠BCO=90°,
∵AD=2DB,∴AD=AB=2,∴D(-3,2).
把D点坐标代入y=,得m=-6,
∴反比例函数的表达式为y=-,
∵AM=2MO,∴MO=OA=1,即M(-1,0),
把点M与点D的坐标代入y=kx+b中,得
解得
则一次函数的表达式为y=-x-1.(2)把y=3代入y=-,得x=-2,∴N(-2,3),即NC=2,设P(x,y),
∵△OPM的面积与四边形OMNC的面积相等,
∴OM|y|=(OM+NC)·OC,即|y|=9,解得y=±9,
当y=9时,x=-10,
当y=-9时,x=8,
则点P的坐标为(-10,9)或(8,-9).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
