人教版八上数学12.2三角形全等的判定同步练习(Word版,附答案)
文档属性
| 名称 | 人教版八上数学12.2三角形全等的判定同步练习(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 220.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 23:40:42 | ||
图片预览


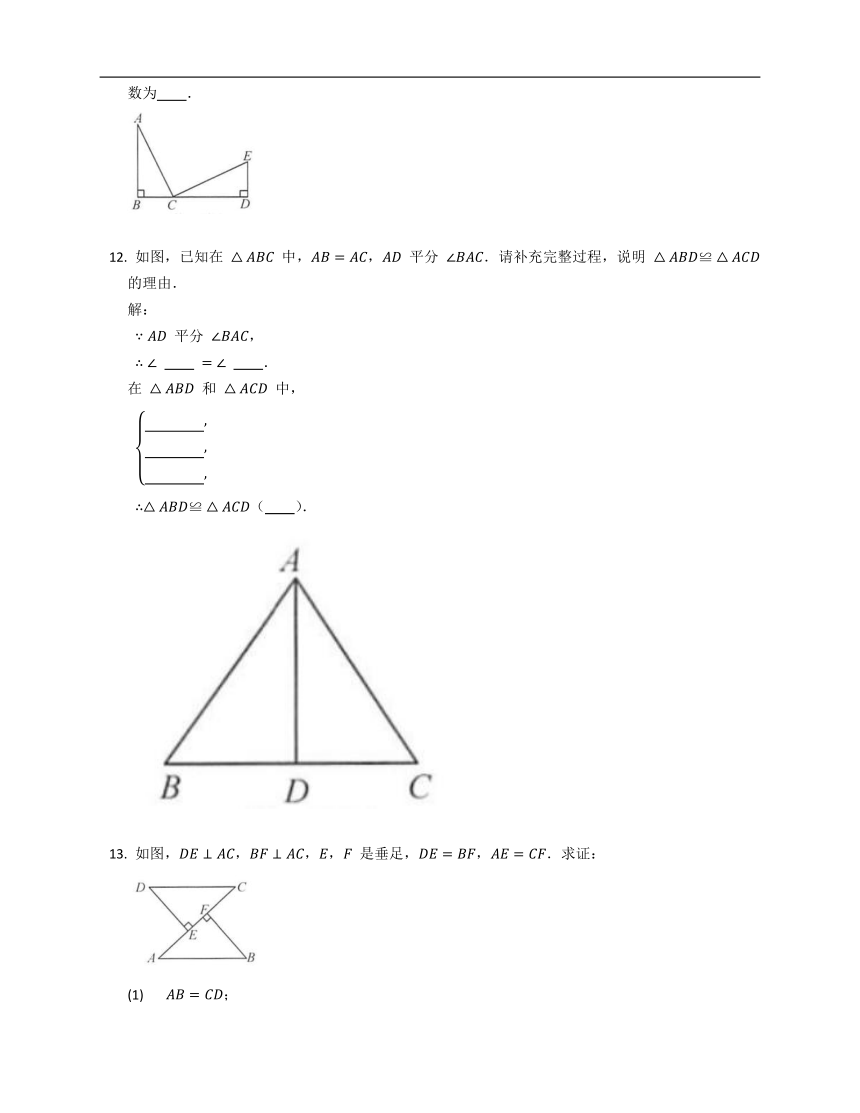

文档简介
人教版八上数学 第12章 第2节 第2课时 三角形全等的判定
两边和它们的 分别相等的两个三角形 (可以简写成“ ”或“ ”).
如果两个三角形两边及其中一边所对的角相等,那么这两个三角形 (填“一定”或“不一定”)全等.
如图,已知 为 的中线.
(1) 求证 .
(2) 若 ,,直接写出 的取值范围.
如图,,,, 四点在同一直线上.,,.求证 .
如图,在四边形 中,,,若连接对角线 , 相交于点 ,则图中全等三角形共有
A. 对 B. 对 C. 对 D. 对
如图,已知 ,,根据“”判定方法,要使 ,则应添加的一个条件为 .
能判定 的条件是
A. ,,
B. ,,
C. ,,
D. ,,
如图,,,欲证 ,可补充条件
A. B. C. D.
如图,把长短确定的两根木棍 , 的一端固定在点 处,和第三根木棍 摆出 ,木棍 固定,木棍 绕点 转动,得到 ,这个实验说明 .
如图,,,则下列结论正确的是 (填序号).
① ;
② ;
③ ;
④ 平分 .
如图,已知 ,垂足为 ,,垂足为 ,,,则 的度数为 .
如图,已知在 中,, 平分 .请补充完整过程,说明 的理由.
解:
平分 ,
.
在 和 中,
( ).
如图,,,, 是垂足,,.求证:
(1) ;
(2) .
试证明“如果两个三角形的两边以及第三边上的中线对应相等,那么这两个三角形全等.”即:如图,在 和 中,,, 和 是中线,且 .求证 .
如图,, 为 的中点,那么下列结论不正确的是
A. B.
C. 平分 D.
如图,, 且 ,,有下列结论:① ;② ;③ .其中正确的结论是
A.①② B.①②③ C.①③ D.②③
在一个三角形中,已知一个角为 ,两条边长为 和 ,符合条件且互不全等的三角形有 个.
如图,在 中, 为 的中点, 为 上一点, 交 于点 ,延长 至点 ,使 ,连接 .
(1) 求证 .
(2) 求证 .
已知在 和 中,,,, 与 交于点 .
(1) 如图①,当 时,求证:
① ;
② .
(2) 如图②,当 时, 的度数为 .
(3) 如图③, 的度数为 (用含 的式子表示).
答案
1. 【答案】夹角;全等;边角边;
2. 【答案】略
3. 【答案】
(1) 如图,延长 至点 ,使 ,连接 ,则 .
为 的中线,
.
在 和 中,
,
.
在 中,根据三角形的三边关系有 ,
而 ,,
.
(2) .
【解析】
(2) 在 中,利用三角形的三边关系推导,得 .
4. 【答案】 ,
,
.
在 和 中
,
.
在 和 中
,
,
.
5. 【答案】C
【解析】 ,, 为公共边,因此 ,
所以 ,,
所以 ,.
6. 【答案】
【解析】可以添加条件 .由条件 ,可得 ,
再加上已知条件 ,根据“”判定方法可得 .
7. 【答案】D
8. 【答案】A
9. 【答案】有两边和其中一边的对角分别相等的两个三角形不一定全等
10. 【答案】①②③
11. 【答案】
12. 【答案】 ; ; ; ; ;
13. 【答案】
(1) ,,
,
.
又 ,
,
.
(2) 由()可知 ,
.
14. 【答案】延长 至 ,使 ,连接 .
延长 至 ,使 ,连接 .
证 ,得 ,.
同理 ,,得 .
再证 ,得 ,
根据“”证 .
15. 【答案】D
16. 【答案】B
17. 【答案】
18. 【答案】
(1) 由点 为 的中点,,利用“”,即可判定 ,.
(2) 首先连接 ,利用“”,即可判定 ,可得 ,
在 中由三角形三边关系,即可证得 .
19. 【答案】
(1) ① ,
,即 .
②在 和 中,
,
,
,
,
,
.
(2)
(3)
两边和它们的 分别相等的两个三角形 (可以简写成“ ”或“ ”).
如果两个三角形两边及其中一边所对的角相等,那么这两个三角形 (填“一定”或“不一定”)全等.
如图,已知 为 的中线.
(1) 求证 .
(2) 若 ,,直接写出 的取值范围.
如图,,,, 四点在同一直线上.,,.求证 .
如图,在四边形 中,,,若连接对角线 , 相交于点 ,则图中全等三角形共有
A. 对 B. 对 C. 对 D. 对
如图,已知 ,,根据“”判定方法,要使 ,则应添加的一个条件为 .
能判定 的条件是
A. ,,
B. ,,
C. ,,
D. ,,
如图,,,欲证 ,可补充条件
A. B. C. D.
如图,把长短确定的两根木棍 , 的一端固定在点 处,和第三根木棍 摆出 ,木棍 固定,木棍 绕点 转动,得到 ,这个实验说明 .
如图,,,则下列结论正确的是 (填序号).
① ;
② ;
③ ;
④ 平分 .
如图,已知 ,垂足为 ,,垂足为 ,,,则 的度数为 .
如图,已知在 中,, 平分 .请补充完整过程,说明 的理由.
解:
平分 ,
.
在 和 中,
( ).
如图,,,, 是垂足,,.求证:
(1) ;
(2) .
试证明“如果两个三角形的两边以及第三边上的中线对应相等,那么这两个三角形全等.”即:如图,在 和 中,,, 和 是中线,且 .求证 .
如图,, 为 的中点,那么下列结论不正确的是
A. B.
C. 平分 D.
如图,, 且 ,,有下列结论:① ;② ;③ .其中正确的结论是
A.①② B.①②③ C.①③ D.②③
在一个三角形中,已知一个角为 ,两条边长为 和 ,符合条件且互不全等的三角形有 个.
如图,在 中, 为 的中点, 为 上一点, 交 于点 ,延长 至点 ,使 ,连接 .
(1) 求证 .
(2) 求证 .
已知在 和 中,,,, 与 交于点 .
(1) 如图①,当 时,求证:
① ;
② .
(2) 如图②,当 时, 的度数为 .
(3) 如图③, 的度数为 (用含 的式子表示).
答案
1. 【答案】夹角;全等;边角边;
2. 【答案】略
3. 【答案】
(1) 如图,延长 至点 ,使 ,连接 ,则 .
为 的中线,
.
在 和 中,
,
.
在 中,根据三角形的三边关系有 ,
而 ,,
.
(2) .
【解析】
(2) 在 中,利用三角形的三边关系推导,得 .
4. 【答案】 ,
,
.
在 和 中
,
.
在 和 中
,
,
.
5. 【答案】C
【解析】 ,, 为公共边,因此 ,
所以 ,,
所以 ,.
6. 【答案】
【解析】可以添加条件 .由条件 ,可得 ,
再加上已知条件 ,根据“”判定方法可得 .
7. 【答案】D
8. 【答案】A
9. 【答案】有两边和其中一边的对角分别相等的两个三角形不一定全等
10. 【答案】①②③
11. 【答案】
12. 【答案】 ; ; ; ; ;
13. 【答案】
(1) ,,
,
.
又 ,
,
.
(2) 由()可知 ,
.
14. 【答案】延长 至 ,使 ,连接 .
延长 至 ,使 ,连接 .
证 ,得 ,.
同理 ,,得 .
再证 ,得 ,
根据“”证 .
15. 【答案】D
16. 【答案】B
17. 【答案】
18. 【答案】
(1) 由点 为 的中点,,利用“”,即可判定 ,.
(2) 首先连接 ,利用“”,即可判定 ,可得 ,
在 中由三角形三边关系,即可证得 .
19. 【答案】
(1) ① ,
,即 .
②在 和 中,
,
,
,
,
,
.
(2)
(3)
