轴对称
图片预览



文档简介
(共11张PPT)
12.1 轴对称(二)
邹泽权
.
.
A1
l
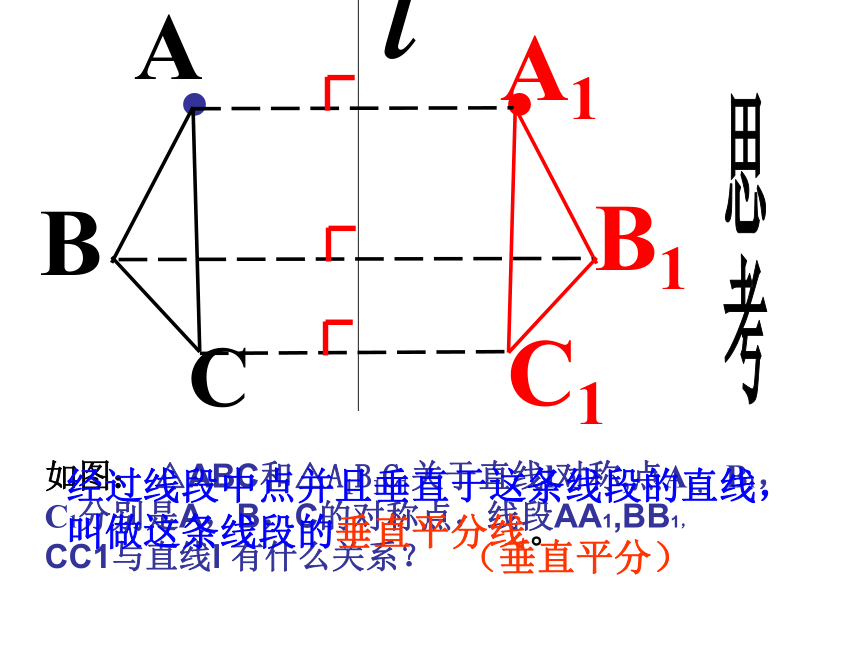
如图: △ABC和△A1B1C1关于直线l对称,点A1, B1,
C1分别是A,B,C的对称点,线段AA1,BB1,
CC1与直线l 有什么关系?
A
B
C
C1
B1
(垂直平分)
经过线段中点并且垂直于这条线段的直线,
叫做这条线段的垂直平分线。
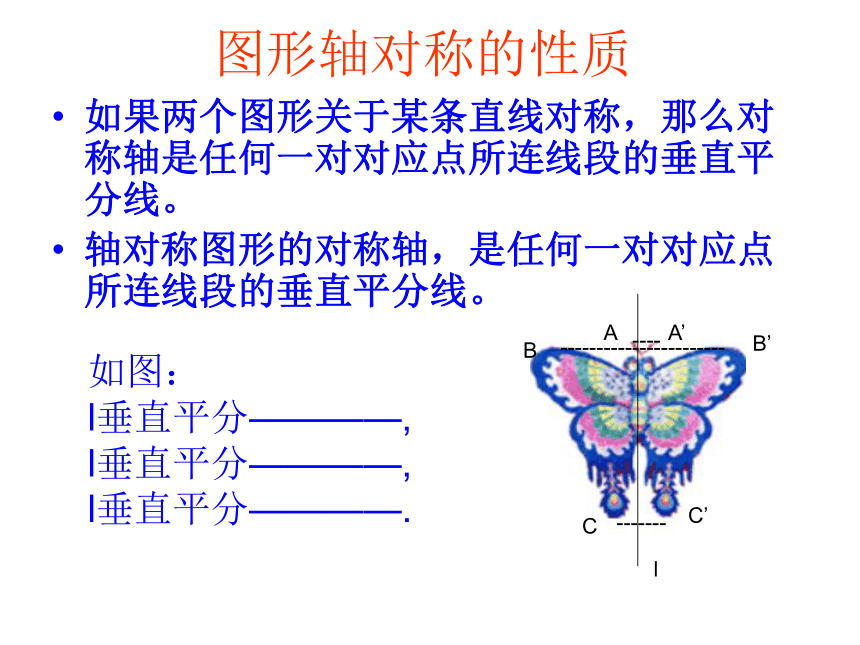
图形轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
l
A
A’
B
B’
C
C’
----
-----------------------
-------
如图:
l垂直平分————,
l垂直平分————,
l垂直平分————.
探究 P32
由此我们可以得出线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的
距离相等。
你能证明这个性质吗?
反过来还成立吗?
结论:与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
你能证明这个结论吗?
从上面两个结论可以看出:在线段AB的垂直平分线l上的点与A,B的距离都相等;反过来,与A,B的距离相等的点都在l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合。
练习:P34 练习 1、2
例、 如图,点A和点B关于某条直线成轴对称,你能作出这条对称轴吗?
A
B
分析:我们只要连接点A和点B,画出线段AB的垂直平分线,就可以得到点A和B的对称轴。而由两点确定一条直线和线段垂直平分线的性质,只要作出到点A,B距离相等的两点即可。
作法
2、分别以点A、B为圆心,大于
的长为半径作弧(为什么),两弧相交于C、D两点
3、 作直线CD。
CD就是所求的直线
1、连接AB
C
D
思考:怎样得到图形的对称轴?
聚焦中考
△ABC中,AB>AC ,∠A的平分线与BC的垂直平分线DM相交于D,过D作DE ⊥AB于E,作DF⊥AC于F,求证:BE=CF
A
B
C
D
E
F
M
小结:
如果两个图形关于某条直线对称,那么对
称轴是任何一对对应点所连线段的垂直平分线。
轴对称图形的对称轴,是任何一对对应点
所连线段的垂直平分线。
线段垂直平分线上的点与这条线段两个端点的距离相等。
与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
①
①
①
①
②
②
②
②
③
④
③
④
③
√
作业:P37-38
5、9、10、11、12
注9、10、11不抄题
12.1 轴对称(二)
邹泽权
.
.
A1
l
如图: △ABC和△A1B1C1关于直线l对称,点A1, B1,
C1分别是A,B,C的对称点,线段AA1,BB1,
CC1与直线l 有什么关系?
A
B
C
C1
B1
(垂直平分)
经过线段中点并且垂直于这条线段的直线,
叫做这条线段的垂直平分线。
图形轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
l
A
A’
B
B’
C
C’
----
-----------------------
-------
如图:
l垂直平分————,
l垂直平分————,
l垂直平分————.
探究 P32
由此我们可以得出线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的
距离相等。
你能证明这个性质吗?
反过来还成立吗?
结论:与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
你能证明这个结论吗?
从上面两个结论可以看出:在线段AB的垂直平分线l上的点与A,B的距离都相等;反过来,与A,B的距离相等的点都在l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合。
练习:P34 练习 1、2
例、 如图,点A和点B关于某条直线成轴对称,你能作出这条对称轴吗?
A
B
分析:我们只要连接点A和点B,画出线段AB的垂直平分线,就可以得到点A和B的对称轴。而由两点确定一条直线和线段垂直平分线的性质,只要作出到点A,B距离相等的两点即可。
作法
2、分别以点A、B为圆心,大于
的长为半径作弧(为什么),两弧相交于C、D两点
3、 作直线CD。
CD就是所求的直线
1、连接AB
C
D
思考:怎样得到图形的对称轴?
聚焦中考
△ABC中,AB>AC ,∠A的平分线与BC的垂直平分线DM相交于D,过D作DE ⊥AB于E,作DF⊥AC于F,求证:BE=CF
A
B
C
D
E
F
M
小结:
如果两个图形关于某条直线对称,那么对
称轴是任何一对对应点所连线段的垂直平分线。
轴对称图形的对称轴,是任何一对对应点
所连线段的垂直平分线。
线段垂直平分线上的点与这条线段两个端点的距离相等。
与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
①
①
①
①
②
②
②
②
③
④
③
④
③
√
作业:P37-38
5、9、10、11、12
注9、10、11不抄题
