2021-2022学年上学期高二数学3.2.2《双曲线的简单几何性质》课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年上学期高二数学3.2.2《双曲线的简单几何性质》课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 00:00:00 | ||
图片预览


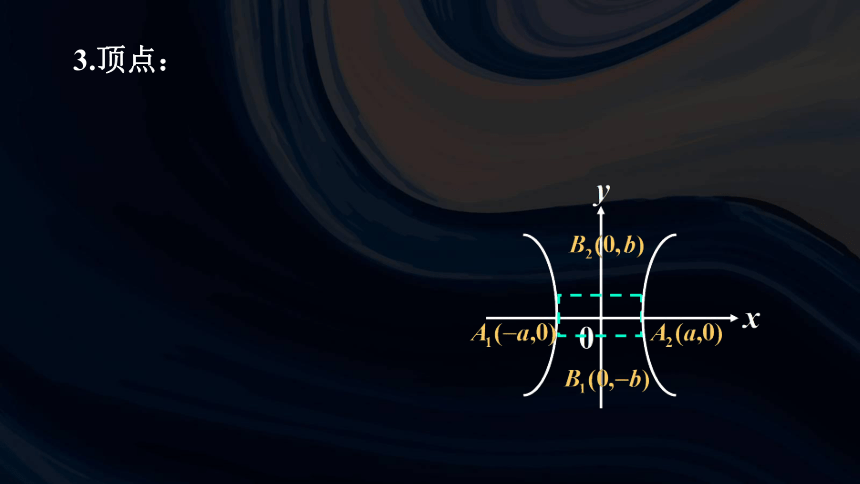



文档简介
(共25张PPT)
3、双曲线方程与椭圆方程之间的区别
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
F (±c, 0)
a>0, b>0, 但a不一定大于b, c2=a2+b2
a>b>0,a2=b2+c2
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
F (0, ±c)
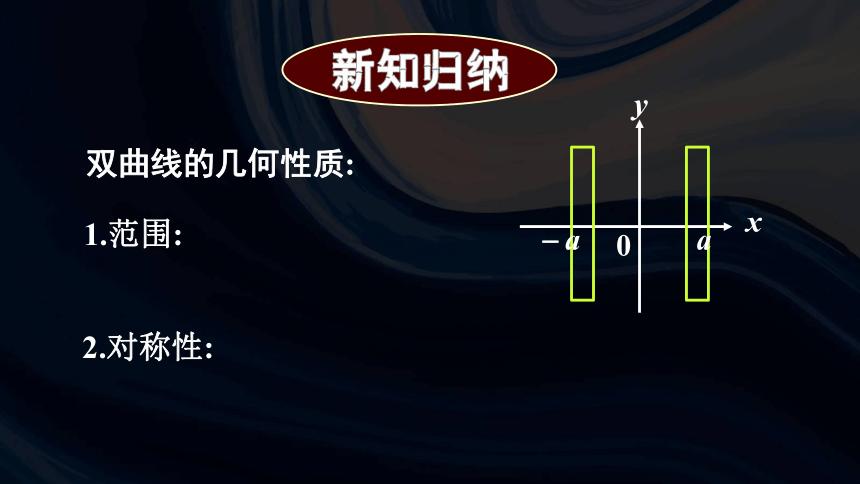
双曲线的几何性质:
2.对称性:
1.范围:
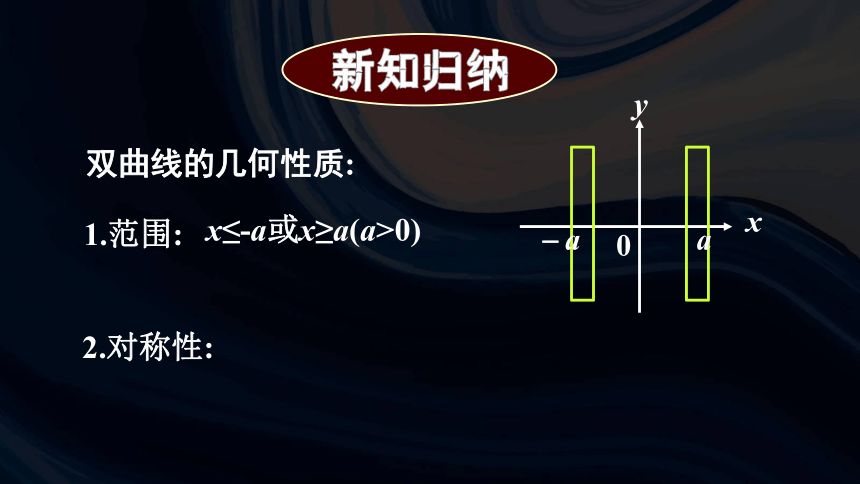
双曲线的几何性质:
2.对称性:
1.范围:
x≤-a或x≥a(a>0)
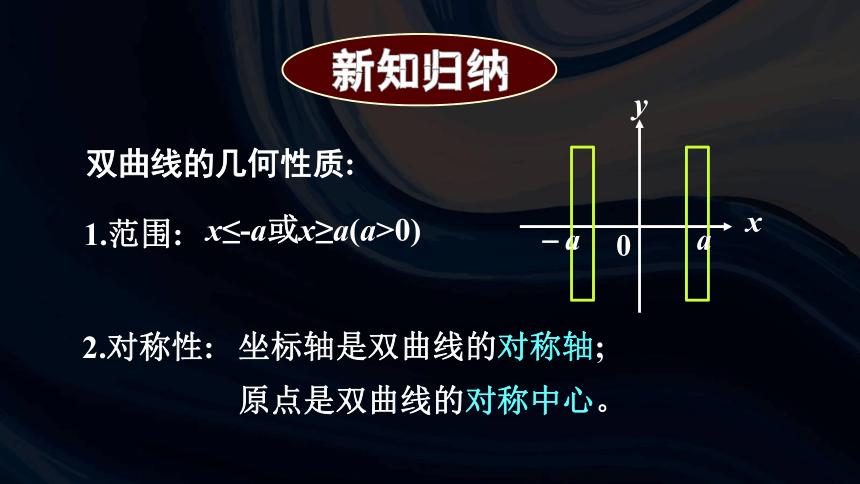
双曲线的几何性质:
2.对称性:
1.范围:
x≤-a或x≥a(a>0)
坐标轴是双曲线的对称轴;
原点是双曲线的对称中心。
3.顶点:
3.顶点:
双曲线与它的对称轴的交点即为双曲线的顶点;A1(-a, 0), A2(a, 0)
3.顶点:
线段A1A2叫双曲线的实轴, 线段B1B2叫双曲线的虚轴.
双曲线与它的对称轴的交点即为双曲线的顶点;A1(-a, 0), A2(a, 0)
3.顶点:
线段A1A2叫双曲线的实轴, 线段B1B2叫双曲线的虚轴.
双曲线与它的对称轴的交点即为双曲线的顶点;A1(-a, 0), A2(a, 0)
a叫双曲线的半实轴长,
b叫双曲线的半虚轴长。
①渐近线的求法:
将双曲线标准方程中1改成0, 即可推出;
①渐近线的求法:
将双曲线标准方程中1改成0, 即可推出;
②渐近线的作用:
1)可协助绘制双曲线图象;
2)研究双曲线的开口程度。
若实轴和虚轴等长的双曲线叫做等轴双曲线. (即a=b的时候),即:
5. 离心率:
例1
例2
思考:(1)
思考:(1)
|MF1|=|a+ex0|,|MF2|=|a-ex0|.
例3
图象
范围
对称性
顶点
焦点
渐近线
离心率
双曲线
性质
图象
范围
对称性 关于坐标轴和原点都对称
顶点
焦点
渐近线
离心率
双曲线
性质
双曲线图像中一个重要的RT△
双曲线图像中一个重要的RT△
双曲线图像中一个重要的RT△
3、双曲线方程与椭圆方程之间的区别
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
F (±c, 0)
a>0, b>0, 但a不一定大于b, c2=a2+b2
a>b>0,a2=b2+c2
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
F (0, ±c)
双曲线的几何性质:
2.对称性:
1.范围:
双曲线的几何性质:
2.对称性:
1.范围:
x≤-a或x≥a(a>0)
双曲线的几何性质:
2.对称性:
1.范围:
x≤-a或x≥a(a>0)
坐标轴是双曲线的对称轴;
原点是双曲线的对称中心。
3.顶点:
3.顶点:
双曲线与它的对称轴的交点即为双曲线的顶点;A1(-a, 0), A2(a, 0)
3.顶点:
线段A1A2叫双曲线的实轴, 线段B1B2叫双曲线的虚轴.
双曲线与它的对称轴的交点即为双曲线的顶点;A1(-a, 0), A2(a, 0)
3.顶点:
线段A1A2叫双曲线的实轴, 线段B1B2叫双曲线的虚轴.
双曲线与它的对称轴的交点即为双曲线的顶点;A1(-a, 0), A2(a, 0)
a叫双曲线的半实轴长,
b叫双曲线的半虚轴长。
①渐近线的求法:
将双曲线标准方程中1改成0, 即可推出;
①渐近线的求法:
将双曲线标准方程中1改成0, 即可推出;
②渐近线的作用:
1)可协助绘制双曲线图象;
2)研究双曲线的开口程度。
若实轴和虚轴等长的双曲线叫做等轴双曲线. (即a=b的时候),即:
5. 离心率:
例1
例2
思考:(1)
思考:(1)
|MF1|=|a+ex0|,|MF2|=|a-ex0|.
例3
图象
范围
对称性
顶点
焦点
渐近线
离心率
双曲线
性质
图象
范围
对称性 关于坐标轴和原点都对称
顶点
焦点
渐近线
离心率
双曲线
性质
双曲线图像中一个重要的RT△
双曲线图像中一个重要的RT△
双曲线图像中一个重要的RT△
