24.3正多边形和圆 同步练习2020-2021学年人教版数学九年级上册(word版含答案)
文档属性
| 名称 | 24.3正多边形和圆 同步练习2020-2021学年人教版数学九年级上册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 758.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 08:23:16 | ||
图片预览

文档简介
正多边形和圆
一、单选题
1.圆内接正三角形的边长是,则该圆的半径长是( )
A. B. C. D.
2.以半径为4的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( ).
A. B. C. D.
3.如图,正六边形内接于圆,半径为4,则这个正六边形的边心距为( )
A.2 B. C. D.
4.如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2020时,顶点A的坐标为( )
A.(﹣2,2) B.(﹣2,﹣2) C.(2,﹣2) D.(2,2)
5.如图所示,正五边形ABCDE内接于⊙O,则∠ADE的度数是( )
A.60° B.45° C.36° D.30°
6.等边三角形的外接圆面积是内切圆面积的( )
A.3倍 B.5倍 C.4倍 D.2倍
7.若⊙O的内接正n边形的边长与⊙O的半径相等,则( )
A.6 B. C. D.4
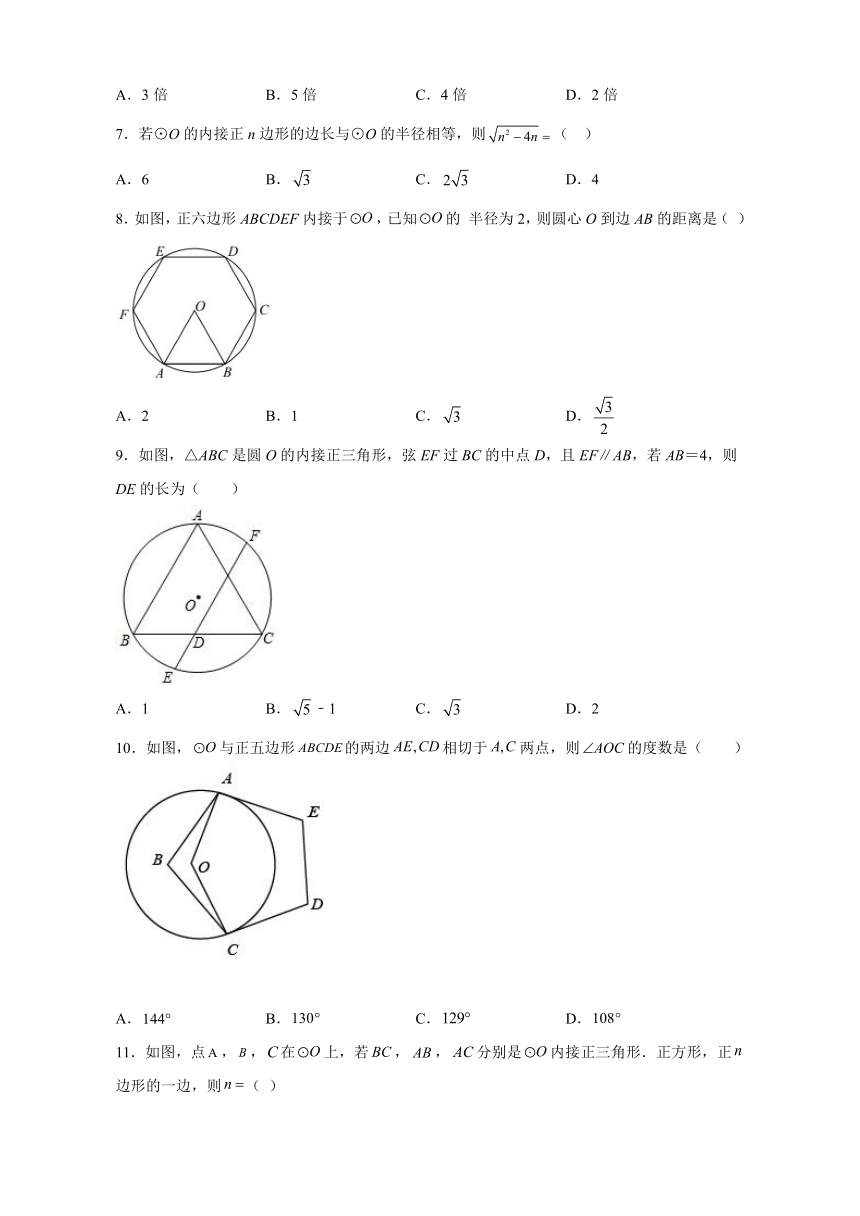
8.如图,正六边形ABCDEF内接于,已知的 半径为2,则圆心O到边AB的距离是( )
A.2 B.1 C. D.
9.如图,△ABC是圆O的内接正三角形,弦EF过BC的中点D,且EF∥AB,若AB=4,则DE的长为( )
A.1 B.﹣1 C. D.2
10.如图,与正五边形的两边相切于两点,则的度数是( )
A. B. C. D.
11.如图,点,,在上,若,,分别是内接正三角形.正方形,正边形的一边,则( )
A.9 B.10 C.12 D.15
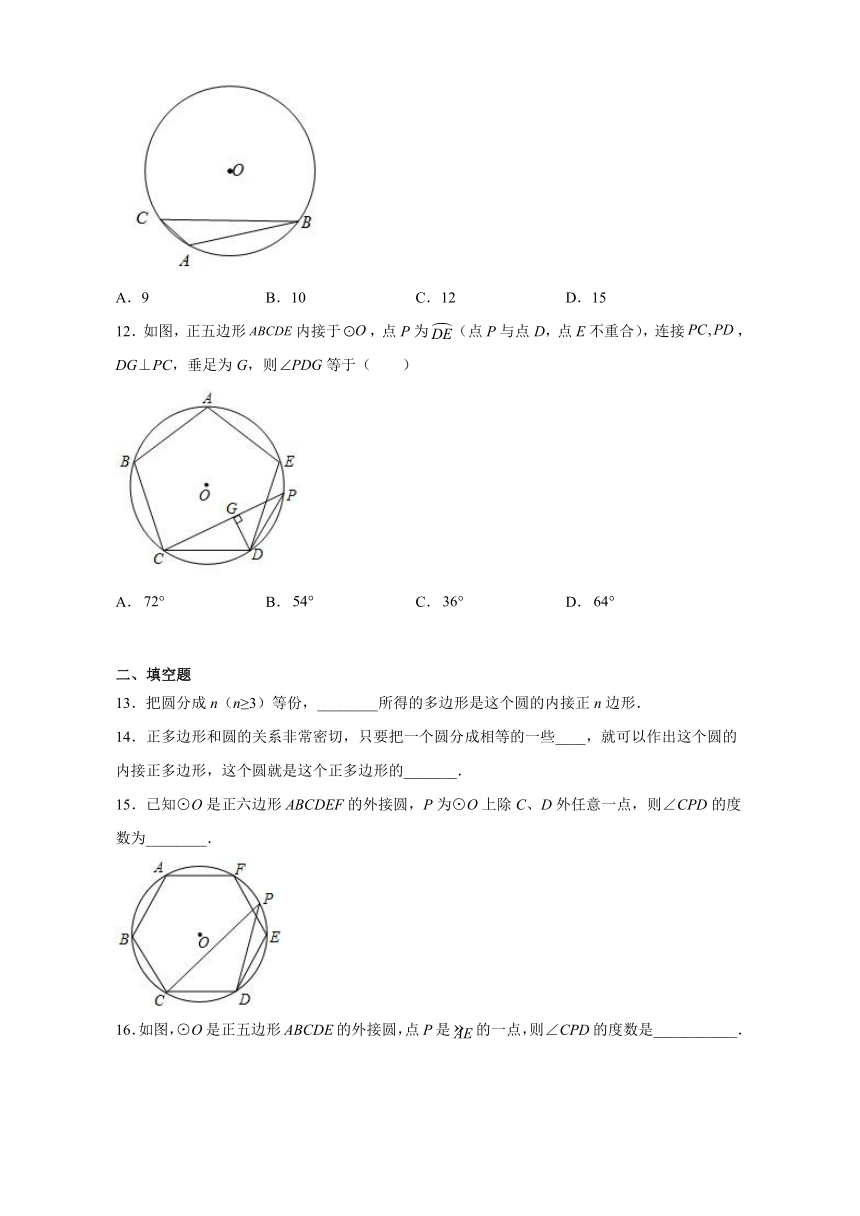
12.如图,正五边形内接于,点P为(点P与点D,点E不重合),连接,DG⊥PC,垂足为G,则等于( )
A. B. C. D.
二、填空题
13.把圆分成n(n≥3)等份,________所得的多边形是这个圆的内接正n边形.
14.正多边形和圆的关系非常密切,只要把一个圆分成相等的一些____,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的_______.
15.已知⊙O是正六边形ABCDEF的外接圆,P为⊙O上除C、D外任意一点,则∠CPD的度数为________.
16.如图,⊙O是正五边形ABCDE的外接圆,点P是的一点,则∠CPD的度数是___________.
17.如图,若五边形是的内接正五边形,则_________,__________,__________,__________.
三、解答题
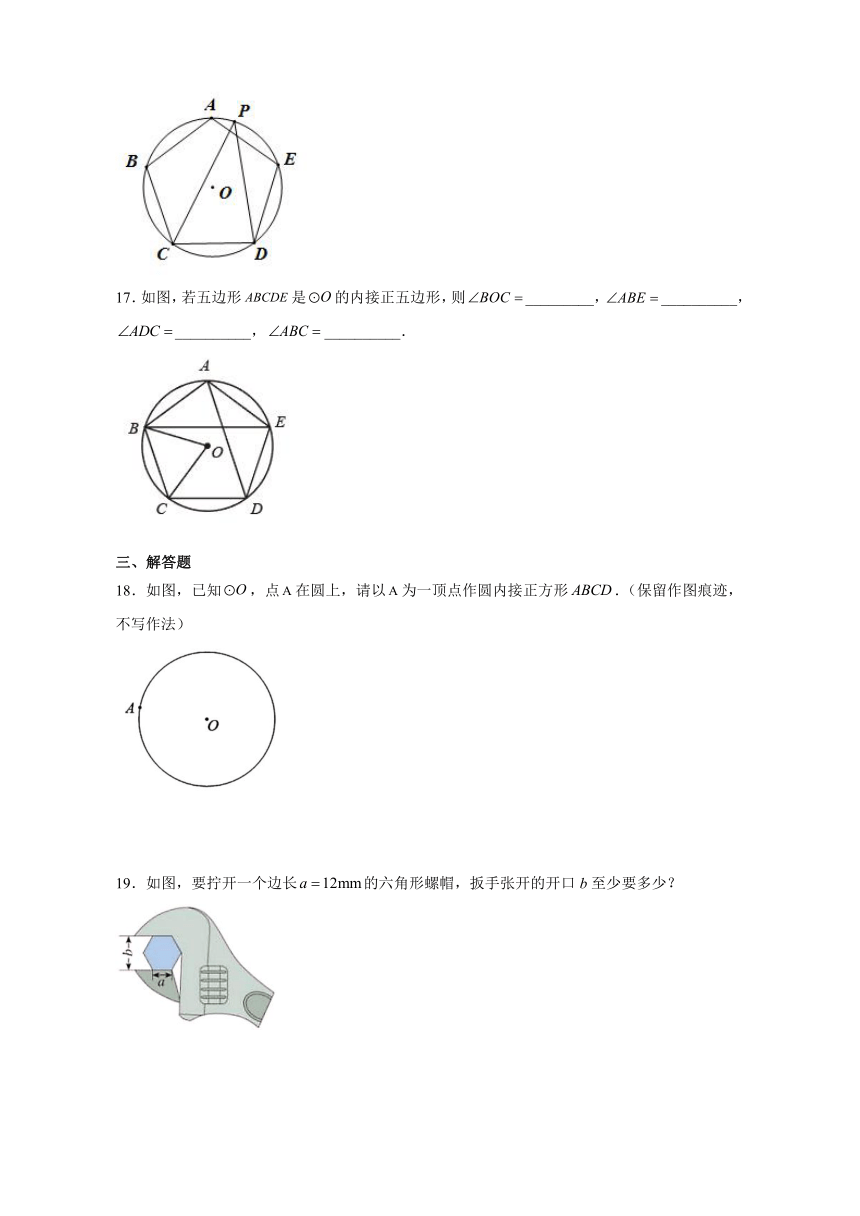
18.如图,已知,点在圆上,请以为一顶点作圆内接正方形.(保留作图痕迹,不写作法)
19.如图,要拧开一个边长的六角形螺帽,扳手张开的开口b至少要多少?
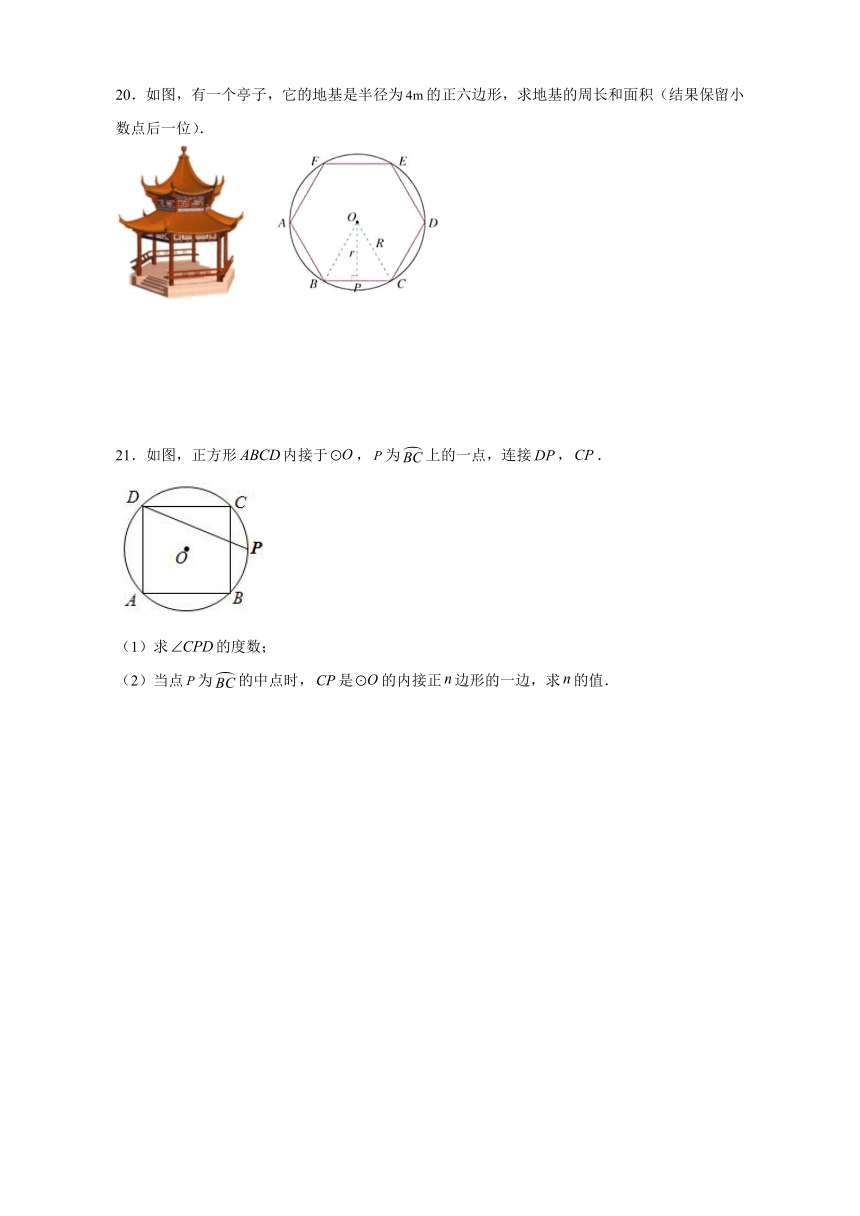
20.如图,有一个亭子,它的地基是半径为的正六边形,求地基的周长和面积(结果保留小数点后一位).
21.如图,正方形内接于,为上的一点,连接,.
(1)求的度数;
(2)当点为的中点时,是的内接正边形的一边,求的值.
参考答案
1.B
解:如图,是边长为12的的内接正三角形.
连,,过点O作于点C,
是正三角形,
∴∠ADB=60°,
∴∠AOB=2∠ADB=120°,
又∵=,
∴∠OAC=∠OBC=30°,
∵,,
,,
∵∠OAC=30°,,
∴设OA=x,则,
在Rt,,
∴,
解得:(舍负),
∴的半径,
故选:B.
2.C
解:如图1,
∵ 为圆内接正三角形,
∴ ,
∵ , ,
∴ ,
如图2,
∵四边形 是圆内接正方形,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,解得: ,
如图3,
∵正六边形为圆内接正六边形,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ 该三角形的三边长分别为 ,
∵ ,
∴该三角形是直角三角形,
∴该三角形的面积为
故选:C
3.B
解:连接,如图所示:
则,
∵,
∴是等边三角形,
∴,
∵,
∴
∴,
故选:B.
4.B
解:连接OA,
∠AOH=30°,AH=2,
∴OH=,
∵六边形ABCDEF是正六边形,
∴点A的坐标为(-2,2),点F的坐标为(2,2),点E的坐标为(4,0),点D的坐标为(2,-2),点C的坐标为(-2,-2),点B的坐标为(-4,0),
∵六边形ABCDEF是正六边形,
∴正六边形ABCDEF绕原点O顺时针旋转6次回到原位置,
2020÷6=336…4,
∴当n=2020时,顶点A与顶点C重合,
∴此时顶点A的坐标为(-2,-2),
故选:B.
5.C
解:略
6.C
解:设是等边三角形的内心,连接,,延长交于,
是等边三角形,
也是的外心,,,
,
等边的外接圆的面积是,
等边的内切圆的面积是,
等边的外接圆面积是内切圆面积的4倍,
故选:C.
7.C
解:∵⊙O的半径与这个正n边形的边长相等,
∴⊙O的两条半径与正n边形的一条边长构成等边三角形,
∵等边三角形的一个内角的度数是60°,
∴这个多边形的中心角=60°,
∴=60°,
∴n=6,
∴,
故选:C.
8.C
解:过O作OH⊥AB于H,
在正六边形ABCDEF中,∠AOB= =60°,
∵OA=OB,
∴∠AOH=30°,AH=AB=1,
∴OH=AH=,
故选C.
9.B
解:如图,连接交于点,连接,,,
△ABC是圆O的内接正三角形,
,,
,
,
是BC的中点,
,
,
,
是BC的中点,AB=4,
,
设,则(),
,
即,
解得,
,
,
,
在中
,
.
故选B.
10.A
解: ∵AE、CD切⊙O于点A、C,
∴∠OAE=90°,∠OCD=90°,
∴正五边形ABCDE的每个内角的度数为: ,
∴∠AOC=540° 90° 90° 108° 108°=144°,
故选:A.
11.C
解:分别连接OB、OA、OC,如图所示
∵是内接正三角形的一边
∴∠BOC=
同理,可得:∠AOB=90°
∴∠AOC=∠BOC ∠AOB=30°
∵是正边形的一边
∴
∴n=12
故选:C.
12.B
解:连接OC,OD.
在正五边形ABCDE中,∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°-36°=54°,
故选:B.
13.顺次连接各分点
解:略
14.弧 外接圆
解:略
15.30°或150°
解:连接OC、OD,如图,
∵⊙O是正六边形ABCDEF的外接圆,
∴∠COD=60°,
当P点在弧CAD上时,∠CPD=∠COD=30°,
当P点在弧CD上时,∠CPD=180°-30°=150°,
综上所述,∠CPD的度数为30°或150°.
故答案为:30°或150°.
16.36°
解:如图,连接OC,OD,
ABCDE是正五边形,
∠COD = ,
∠CPD=∠COD= 36°,
故答案为: 36°.
17.
解:五边形是的内接正五边形,
,
又正五边形的内角和为,
,,
,
又,,
.
故答案为:;;;
18.见详解
解:如图,正方形ABCD为所作.
19.扳手张开的开口b至少要12mm.
解:如图所示,由题意得:六边形为正六边形,
六边形的六条边相等,每个内角为
过点A作AG⊥BF,垂足为点G,
因为∠BAF=120°,
所以∠BAG=60°,
所以∠ABG=30°,
在Rt△ABG中,AB=12mm,∠AGB=90°,∠ABG=30°,
所以AG=AB=×12=6(mm),
由勾股定理得BG===6(mm),
即b=BF=2BG=2×6=12 (mm).
答:扳手张开的开口b至少要12mm.
20.亭子地基的周长为24m,地基的面积为41.6m2.
解:如图,连接.因为六边形是正六边形,所以它的中心角∠BOC等于是等边三角形,从而正六边形的边长等于它的半径.
因此,亭子地基的周长.
作,垂足为P.在中,∠POC=90°-60°=30°
∴,
利用勾股定理,可得边心距.
亭子地基的面积.
21.(1)45°;(2)8
解:(1)连接,,
∵正方形内接于,
∴.
∴;
(2)连接,,
∵正方形内接于,
∴.
∵点为的中点,
∴,
∴∠COP=∠BOP,
∵∠COP+∠BOP=∠COB=90°,
∴,
∴.
一、单选题
1.圆内接正三角形的边长是,则该圆的半径长是( )
A. B. C. D.
2.以半径为4的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( ).
A. B. C. D.
3.如图,正六边形内接于圆,半径为4,则这个正六边形的边心距为( )
A.2 B. C. D.
4.如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2020时,顶点A的坐标为( )
A.(﹣2,2) B.(﹣2,﹣2) C.(2,﹣2) D.(2,2)
5.如图所示,正五边形ABCDE内接于⊙O,则∠ADE的度数是( )
A.60° B.45° C.36° D.30°
6.等边三角形的外接圆面积是内切圆面积的( )
A.3倍 B.5倍 C.4倍 D.2倍
7.若⊙O的内接正n边形的边长与⊙O的半径相等,则( )
A.6 B. C. D.4
8.如图,正六边形ABCDEF内接于,已知的 半径为2,则圆心O到边AB的距离是( )
A.2 B.1 C. D.
9.如图,△ABC是圆O的内接正三角形,弦EF过BC的中点D,且EF∥AB,若AB=4,则DE的长为( )
A.1 B.﹣1 C. D.2
10.如图,与正五边形的两边相切于两点,则的度数是( )
A. B. C. D.
11.如图,点,,在上,若,,分别是内接正三角形.正方形,正边形的一边,则( )
A.9 B.10 C.12 D.15
12.如图,正五边形内接于,点P为(点P与点D,点E不重合),连接,DG⊥PC,垂足为G,则等于( )
A. B. C. D.
二、填空题
13.把圆分成n(n≥3)等份,________所得的多边形是这个圆的内接正n边形.
14.正多边形和圆的关系非常密切,只要把一个圆分成相等的一些____,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的_______.
15.已知⊙O是正六边形ABCDEF的外接圆,P为⊙O上除C、D外任意一点,则∠CPD的度数为________.
16.如图,⊙O是正五边形ABCDE的外接圆,点P是的一点,则∠CPD的度数是___________.
17.如图,若五边形是的内接正五边形,则_________,__________,__________,__________.
三、解答题
18.如图,已知,点在圆上,请以为一顶点作圆内接正方形.(保留作图痕迹,不写作法)
19.如图,要拧开一个边长的六角形螺帽,扳手张开的开口b至少要多少?
20.如图,有一个亭子,它的地基是半径为的正六边形,求地基的周长和面积(结果保留小数点后一位).
21.如图,正方形内接于,为上的一点,连接,.
(1)求的度数;
(2)当点为的中点时,是的内接正边形的一边,求的值.
参考答案
1.B
解:如图,是边长为12的的内接正三角形.
连,,过点O作于点C,
是正三角形,
∴∠ADB=60°,
∴∠AOB=2∠ADB=120°,
又∵=,
∴∠OAC=∠OBC=30°,
∵,,
,,
∵∠OAC=30°,,
∴设OA=x,则,
在Rt,,
∴,
解得:(舍负),
∴的半径,
故选:B.
2.C
解:如图1,
∵ 为圆内接正三角形,
∴ ,
∵ , ,
∴ ,
如图2,
∵四边形 是圆内接正方形,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,解得: ,
如图3,
∵正六边形为圆内接正六边形,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ 该三角形的三边长分别为 ,
∵ ,
∴该三角形是直角三角形,
∴该三角形的面积为
故选:C
3.B
解:连接,如图所示:
则,
∵,
∴是等边三角形,
∴,
∵,
∴
∴,
故选:B.
4.B
解:连接OA,
∠AOH=30°,AH=2,
∴OH=,
∵六边形ABCDEF是正六边形,
∴点A的坐标为(-2,2),点F的坐标为(2,2),点E的坐标为(4,0),点D的坐标为(2,-2),点C的坐标为(-2,-2),点B的坐标为(-4,0),
∵六边形ABCDEF是正六边形,
∴正六边形ABCDEF绕原点O顺时针旋转6次回到原位置,
2020÷6=336…4,
∴当n=2020时,顶点A与顶点C重合,
∴此时顶点A的坐标为(-2,-2),
故选:B.
5.C
解:略
6.C
解:设是等边三角形的内心,连接,,延长交于,
是等边三角形,
也是的外心,,,
,
等边的外接圆的面积是,
等边的内切圆的面积是,
等边的外接圆面积是内切圆面积的4倍,
故选:C.
7.C
解:∵⊙O的半径与这个正n边形的边长相等,
∴⊙O的两条半径与正n边形的一条边长构成等边三角形,
∵等边三角形的一个内角的度数是60°,
∴这个多边形的中心角=60°,
∴=60°,
∴n=6,
∴,
故选:C.
8.C
解:过O作OH⊥AB于H,
在正六边形ABCDEF中,∠AOB= =60°,
∵OA=OB,
∴∠AOH=30°,AH=AB=1,
∴OH=AH=,
故选C.
9.B
解:如图,连接交于点,连接,,,
△ABC是圆O的内接正三角形,
,,
,
,
是BC的中点,
,
,
,
是BC的中点,AB=4,
,
设,则(),
,
即,
解得,
,
,
,
在中
,
.
故选B.
10.A
解: ∵AE、CD切⊙O于点A、C,
∴∠OAE=90°,∠OCD=90°,
∴正五边形ABCDE的每个内角的度数为: ,
∴∠AOC=540° 90° 90° 108° 108°=144°,
故选:A.
11.C
解:分别连接OB、OA、OC,如图所示
∵是内接正三角形的一边
∴∠BOC=
同理,可得:∠AOB=90°
∴∠AOC=∠BOC ∠AOB=30°
∵是正边形的一边
∴
∴n=12
故选:C.
12.B
解:连接OC,OD.
在正五边形ABCDE中,∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°-36°=54°,
故选:B.
13.顺次连接各分点
解:略
14.弧 外接圆
解:略
15.30°或150°
解:连接OC、OD,如图,
∵⊙O是正六边形ABCDEF的外接圆,
∴∠COD=60°,
当P点在弧CAD上时,∠CPD=∠COD=30°,
当P点在弧CD上时,∠CPD=180°-30°=150°,
综上所述,∠CPD的度数为30°或150°.
故答案为:30°或150°.
16.36°
解:如图,连接OC,OD,
ABCDE是正五边形,
∠COD = ,
∠CPD=∠COD= 36°,
故答案为: 36°.
17.
解:五边形是的内接正五边形,
,
又正五边形的内角和为,
,,
,
又,,
.
故答案为:;;;
18.见详解
解:如图,正方形ABCD为所作.
19.扳手张开的开口b至少要12mm.
解:如图所示,由题意得:六边形为正六边形,
六边形的六条边相等,每个内角为
过点A作AG⊥BF,垂足为点G,
因为∠BAF=120°,
所以∠BAG=60°,
所以∠ABG=30°,
在Rt△ABG中,AB=12mm,∠AGB=90°,∠ABG=30°,
所以AG=AB=×12=6(mm),
由勾股定理得BG===6(mm),
即b=BF=2BG=2×6=12 (mm).
答:扳手张开的开口b至少要12mm.
20.亭子地基的周长为24m,地基的面积为41.6m2.
解:如图,连接.因为六边形是正六边形,所以它的中心角∠BOC等于是等边三角形,从而正六边形的边长等于它的半径.
因此,亭子地基的周长.
作,垂足为P.在中,∠POC=90°-60°=30°
∴,
利用勾股定理,可得边心距.
亭子地基的面积.
21.(1)45°;(2)8
解:(1)连接,,
∵正方形内接于,
∴.
∴;
(2)连接,,
∵正方形内接于,
∴.
∵点为的中点,
∴,
∴∠COP=∠BOP,
∵∠COP+∠BOP=∠COB=90°,
∴,
∴.
同课章节目录
