人教版九年级数学下册 26.1.2反比例函数的图象和性质(共30张PPT)
文档属性
| 名称 | 人教版九年级数学下册 26.1.2反比例函数的图象和性质(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
26.1.2 反比例函数的图象和性质
九年级下册 RJ
初中数学
第2课时
1.能够应用反比例函数的图象和性质解题.
2.理解反比例函数的系数 k 的几何意义,并将其灵活运用于坐标系中图形的面积计算.
3.体会“数”与“形”的相互转化,学习数形结合的思想方法.
学习目标
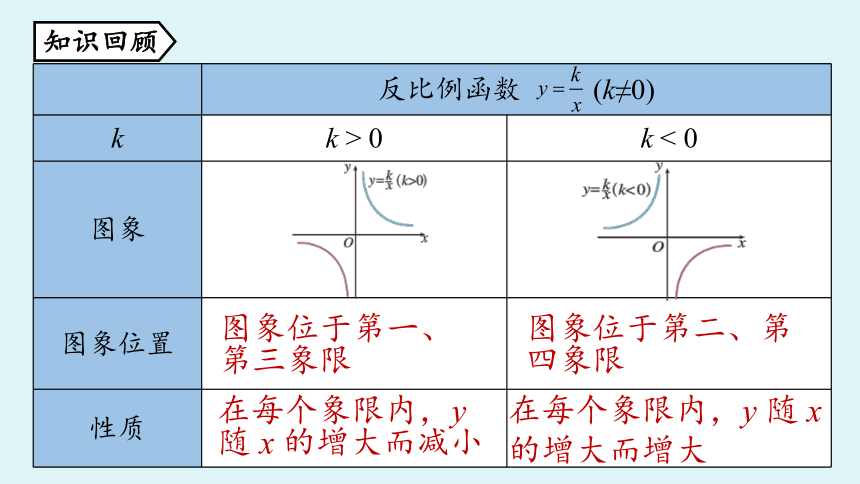
反比例函数 (k≠0) k k > 0 k < 0
图象
图象位置
性质
图象位于第一、第三象限
图象位于第二、第四象限
在每个象限内,y 随 x 的增大而减小
在每个象限内,y 随 x
的增大而增大
知识回顾
上节课我们已经学习了反比例函数的图象和性质,本节课我们将尝试熟练地运用反比例函数的图象和性质解决一些复杂的问题,同学们有信心吗?
课堂导入
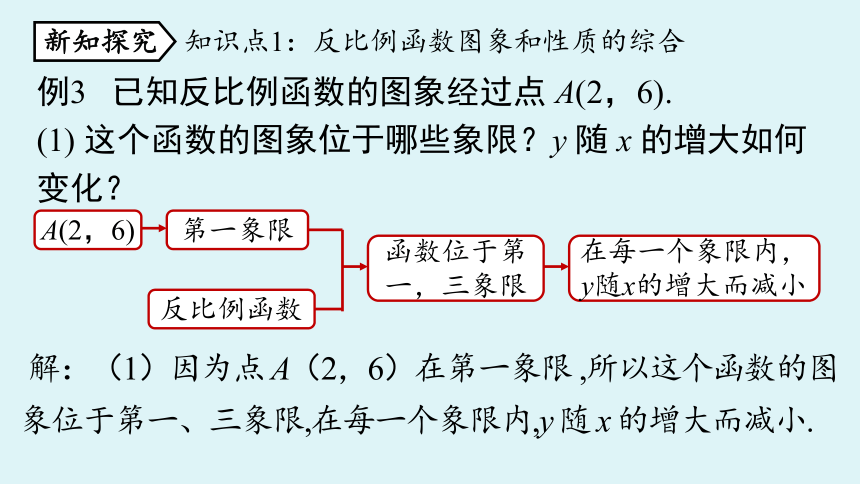
例3 已知反比例函数的图象经过点 A(2,6).
(1) 这个函数的图象位于哪些象限?y 随 x 的增大如何变化?
知识点1:反比例函数图象和性质的综合
新知探究
A(2,6)
第一象限
反比例函数
函数位于第一,三象限
在每一个象限内,y随x的增大而减小
解:(1)因为点 A(2,6)在第一象限 ,所以这个函数的图象位于第一、三象限,在每一个象限内,y 随 x 的增大而减小.
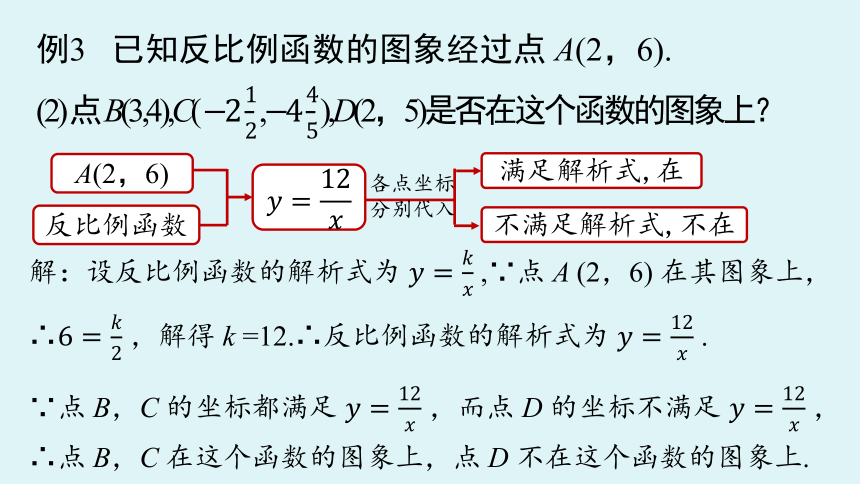
解:设反比例函数的解析式为 ,∵点 A (2,6) 在其图象上,
∴ ,解得 k =12.∴反比例函数的解析式为 .
∵点 B,C 的坐标都满足 ,而点 D 的坐标不满足 ,
∴点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上.
A(2,6)
反比例函数
满足解析式,在
各点坐标
分别代入
不满足解析式,不在
例3 已知反比例函数的图象经过点 A(2,6).
(2) 点 B(3,4),C( , ),D(2,5)是否在这个函数的图象上?
例4 如图,它是反比例函数 图象的一支. 根据图象,回答下列问题:
图象的另一支位于哪个象限?常数 m 的
取值范围是什么?
解:反比例函数的图象只有两种可能:
位于第一、第三象限,或者位于第二、第四象限.
因为这个函数的图象的一支位于第一象限,
所以另一支必位于第三象限.
因为这个函数的图象位于第一、第三象限,
所以 m-5>0,解得 m>5.
(2) 在这个函数图象的某一支上任取点 A(x1,y1) 和点 B(x2,y2). 如果 x1>x2,那么 y1 和 y2 有怎样的大小关系?
解:因为 m-5 > 0,
所以在这个函数图象的任一支上,
y 都随 x 的增大而减小,
因此当 x1>x2 时,y1<y2.
比较反比例函数值大小的方法
比较反比例函数的函数值时,在同一分支上的点可以利用函数的增减性通过比较其横坐标的大小来判断函数值的大小;不在同一分支上的点,依据与 x 轴的相对位置(在 x 轴上方或 x 轴下方)来进行函数值大小的比较.
另外,图象法和特殊值法也是解决此类问题的常用方法,图象法形象直观,特殊值法简单直接.
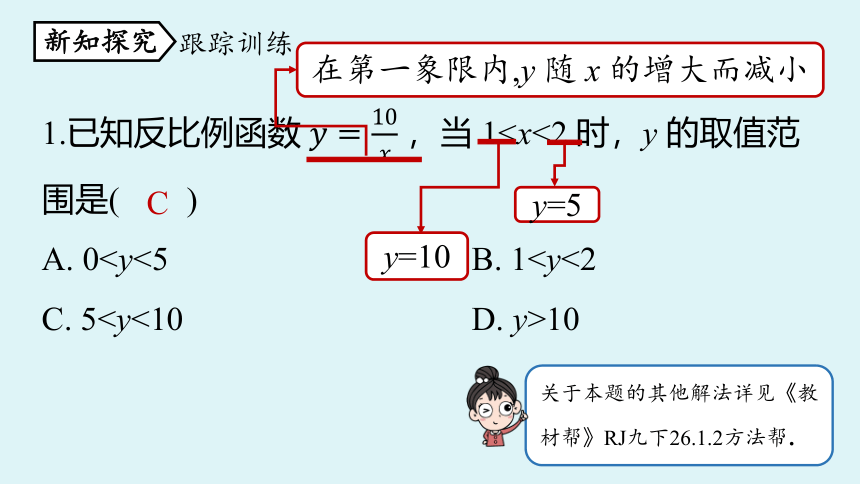
1.已知反比例函数 ,当 1A. 0C. 510
C
在第一象限内,y 随 x 的增大而减小
y=10
y=5
新知探究
跟踪训练
关于本题的其他解法详见《教材帮》RJ九下26.1.2方法帮.
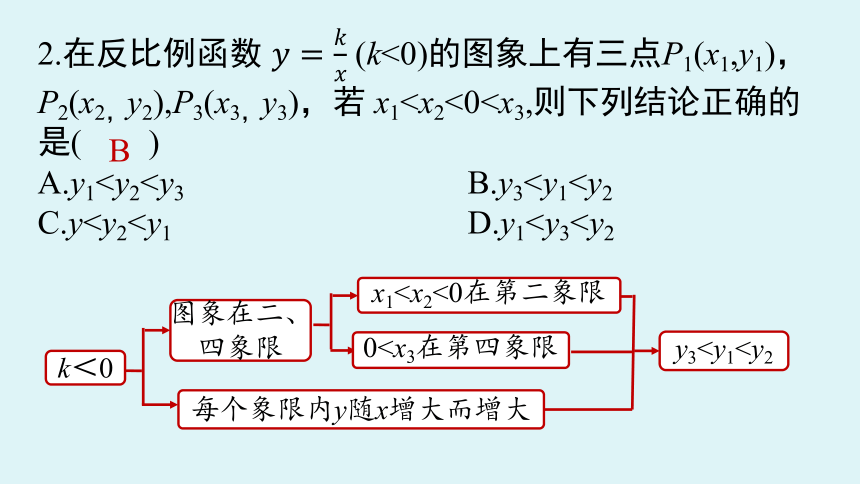
2.在反比例函数 (k<0)的图象上有三点P1(x1,y1),P2(x2,y2),P3(x3,y3),若 x1A.y1C.yB
y3k<0
图象在二、
四象限
x10每个象限内y随x增大而增大
图象法:
因为 k<0,所以反比例函数的图象在第二、第四象限,如图所示,在图中描出符合条件的三个点,观察图象可知 y3B
2.在反比例函数 (k<0)的图象上有三点 P1(x1,y1),P2(x2,y2),P3(x3,y3),若 x1A.y1C.y32.在反比例函数 (k<0)的图象上有三点 P1(x1,y1),P2(x2,y2),P3(x3,y3),若 x1A.y1C.y3特殊值法:
设该反比例函数解析式为 .取满足 x1B
在反比例函数 的图象上分别取点P,Q 向 x 轴、y 轴作垂线,围成面积分别为S1,S2的矩形,填写下面表格:
S1的值 S2的值 S1与S2的关系 猜想 S1,S2 与 k的关系
P (2,2) Q (4,1)
新知探究
知识点2:反比例函数解析式中 k 的几何意义
5
1
2
3
4
-1
x
y
O
P
S1
S2
P (2,2)
Q (4,1)
S1的值
S2的值
S1与S2的关系
S1,S2 与 k的关系
4
4
S1=S2
S1=S2=k
-4
-3
1
4
3
2
-3
-2
-4
-1
Q
-2
若在反比例函数 中也用同样的方法分别取 P,Q 两点,填写表格:
S1的值 S2的值 S1与S2的关系 猜想 S1,S2 与 k的关系
P (-1,4) Q (-2,2)
1
2
3
4
y
x
O
P
Q
S1
S2
P (-1,4)
Q (-2,2)
S1的值
S2的值
S1与S2的关系
S1,S2 与 k的关系
4
4
S1=S2
S1=S2=-k
2
1
-2
-1
-1
-2
3
4
若点 P 是 图象上的任意一点,作 PA 垂直于 x 轴,作 PB 垂直于 y 轴,则矩形 AOBP 的面积与 k 的关系是什么?
S矩形 AOBP=|k|,你能给出证明吗?
B
P
A
y
x
O
P
A
B
设点 P (a,b),∵点 P 在函数 的图象上,∴ ,即 ab=k.
∵S矩形 AOBP=PB·PA=|a|·|b|=|ab,
∴S矩形 AOBP=|k|.
反比例函数 (k≠0)中 k 的几何意义包括以下两种:
(2)如图,过双曲线上的任意一点 E 作 EF⊥y 轴,垂足为 F,连接EO,则S△EOF=.
B
P
A
y
x
O
P
A
B
(1)如图,过双曲线上任意一点 P(x,y)
分别作 x 轴、y 轴的垂线 PM,PN,
则S矩形 AOBP=|k|.
1.如图所示,点 A 是反比例函数图象上一点,过点 A 作 AB⊥y 轴于点 B,点 C,D 在 x 轴上,且 BC//AD,四边形 ABCD 的面积为 3,则这个反比例函数的解析式为 _______________.
A
B
C
D
O
E
y
x
新知探究
跟踪训练
S四边形ABOE =S四边形ABCD=3
|k|=3
图象在第二象限
k<0,x<0
(x<0 )
2.如图,点 A,B 是双曲线 上的点,分别过点 A,B作 x 轴的垂线段,垂足分别为 C,D,连接 OA,OB,若图中阴影部分的面积为1,则△OAE 与四边形 BECD 面积的和为 .
10
S△AOC= S△BOD =6
k=12
S阴影=1
S△OAE =5,
S四边形BECD =5
1.已知点 A(x1,3),B(x2,6)都在反比例函数 的图象上,则下列关系式一定正确的是( )
A.x1C.x2A
随堂练习
在每一象限内,y 随 x 的增大而增大
2.如图所示,点 A 在双曲线 上,点 B 在双曲线 上,且 AB//x 轴,则△OAB 的面积= .
C
点 B在 上
S△OBC=4
S△AOC=
点 A 在 上
S△OAB=
3.如图,已知 A(-4,2),B(n,-4)两点是一次函数 y=kx+b 和反比例函数 图象的两个交点.
(1)求一次函数和反比例函数的解析式;
解:(1)∵A(-4,2)在 y= 上,
∴m=2×(-4)=-8,∴ B(2,-4).
把 A(-4,2)和 B(2,-4)的坐标分别代入 y=kx+b,
得 解得
∴一次函数、反比例函数的解析式分别为 y = -x-2,y= .
解:(2) y = -x-2中,令 y=0,则 x=-2,
即 C(-2,0),
所以 S△AOB=S△AOC+S△BOC= =6.
3.如图,已知 A(-4,2),B(n,-4)两点是一次函数 y=kx+b 和反比例函数 图象的两个交点.
(2)求△AOB 的面积;
解:(3)不等式 的解集,
即不等式 的解集,
由图可得,不等式 的解集为 x<-4或 03.如图,已知 A(-4,2),B(n,-4)两点是一次函数 y=kx+b 和反比例函数 图象的两个交点.
(3)观察图象,直接写出不等式 的解集.
反比例函数
图象
性质
k 的几何意义
画法
形状
图象位置
增减性
列表、描点、连线
双曲线
课堂小结
对接中考
1.(2021 金华中考)已知点A(x1,y1),B(x2,y2)在反比例函数y=﹣ 的图象上.若x1<0<x2,则( )
A.y1<0<y2 B.y2<0<y1
C.y1<y2<0 D.y2<y1<0
解析:∵k=﹣12<0,∴双曲线在第二,四象限,∵x1<0<x2,∴点A在第二象限,点B在第四象限,∴y2<0<y1.
B
2.(2021 南京中考)如图,正比例函数y=kx与函数y= 的图象交于A,B两点,BC∥x轴,AC∥y轴,则S△ABC=__________.
解析:连接OC,设AC交x轴于点N,BC交y
轴于M点,∴S△AON=S△OBM =3.
12
N
M
∵BC∥x轴,AC∥y轴,∴S△AON=S△CON,S△OBM=S△OCM,
∴S△ABC=4S△AON=4× 3 =12.
3.(2021 苏州中考)如图,在平面直角坐标系中,四边形OABC为矩形,点C,A分别在x轴和y轴的正半轴上,点D为AB的中点.已知实数k≠0,一次函数y=﹣3x+k的图象经过点C,D,反比例函数y= (x>0)的图象经过点B,求k的值.
解:令y=0,则0=﹣3x+k,得x= ,∴C( ,0),
∴B( ,3).∵点D为AB的中点,∴D( ,3).
∵点D在直线y=﹣3x+k上,∴3=﹣3× +k,∴ k =6.
k
26.1.2 反比例函数的图象和性质
九年级下册 RJ
初中数学
第2课时
1.能够应用反比例函数的图象和性质解题.
2.理解反比例函数的系数 k 的几何意义,并将其灵活运用于坐标系中图形的面积计算.
3.体会“数”与“形”的相互转化,学习数形结合的思想方法.
学习目标
反比例函数 (k≠0) k k > 0 k < 0
图象
图象位置
性质
图象位于第一、第三象限
图象位于第二、第四象限
在每个象限内,y 随 x 的增大而减小
在每个象限内,y 随 x
的增大而增大
知识回顾
上节课我们已经学习了反比例函数的图象和性质,本节课我们将尝试熟练地运用反比例函数的图象和性质解决一些复杂的问题,同学们有信心吗?
课堂导入
例3 已知反比例函数的图象经过点 A(2,6).
(1) 这个函数的图象位于哪些象限?y 随 x 的增大如何变化?
知识点1:反比例函数图象和性质的综合
新知探究
A(2,6)
第一象限
反比例函数
函数位于第一,三象限
在每一个象限内,y随x的增大而减小
解:(1)因为点 A(2,6)在第一象限 ,所以这个函数的图象位于第一、三象限,在每一个象限内,y 随 x 的增大而减小.
解:设反比例函数的解析式为 ,∵点 A (2,6) 在其图象上,
∴ ,解得 k =12.∴反比例函数的解析式为 .
∵点 B,C 的坐标都满足 ,而点 D 的坐标不满足 ,
∴点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上.
A(2,6)
反比例函数
满足解析式,在
各点坐标
分别代入
不满足解析式,不在
例3 已知反比例函数的图象经过点 A(2,6).
(2) 点 B(3,4),C( , ),D(2,5)是否在这个函数的图象上?
例4 如图,它是反比例函数 图象的一支. 根据图象,回答下列问题:
图象的另一支位于哪个象限?常数 m 的
取值范围是什么?
解:反比例函数的图象只有两种可能:
位于第一、第三象限,或者位于第二、第四象限.
因为这个函数的图象的一支位于第一象限,
所以另一支必位于第三象限.
因为这个函数的图象位于第一、第三象限,
所以 m-5>0,解得 m>5.
(2) 在这个函数图象的某一支上任取点 A(x1,y1) 和点 B(x2,y2). 如果 x1>x2,那么 y1 和 y2 有怎样的大小关系?
解:因为 m-5 > 0,
所以在这个函数图象的任一支上,
y 都随 x 的增大而减小,
因此当 x1>x2 时,y1<y2.
比较反比例函数值大小的方法
比较反比例函数的函数值时,在同一分支上的点可以利用函数的增减性通过比较其横坐标的大小来判断函数值的大小;不在同一分支上的点,依据与 x 轴的相对位置(在 x 轴上方或 x 轴下方)来进行函数值大小的比较.
另外,图象法和特殊值法也是解决此类问题的常用方法,图象法形象直观,特殊值法简单直接.
1.已知反比例函数 ,当 1
C
在第一象限内,y 随 x 的增大而减小
y=10
y=5
新知探究
跟踪训练
关于本题的其他解法详见《教材帮》RJ九下26.1.2方法帮.
2.在反比例函数 (k<0)的图象上有三点P1(x1,y1),P2(x2,y2),P3(x3,y3),若 x1
y3
图象在二、
四象限
x1
图象法:
因为 k<0,所以反比例函数的图象在第二、第四象限,如图所示,在图中描出符合条件的三个点,观察图象可知 y3
2.在反比例函数 (k<0)的图象上有三点 P1(x1,y1),P2(x2,y2),P3(x3,y3),若 x1
设该反比例函数解析式为 .取满足 x1
在反比例函数 的图象上分别取点P,Q 向 x 轴、y 轴作垂线,围成面积分别为S1,S2的矩形,填写下面表格:
S1的值 S2的值 S1与S2的关系 猜想 S1,S2 与 k的关系
P (2,2) Q (4,1)
新知探究
知识点2:反比例函数解析式中 k 的几何意义
5
1
2
3
4
-1
x
y
O
P
S1
S2
P (2,2)
Q (4,1)
S1的值
S2的值
S1与S2的关系
S1,S2 与 k的关系
4
4
S1=S2
S1=S2=k
-4
-3
1
4
3
2
-3
-2
-4
-1
Q
-2
若在反比例函数 中也用同样的方法分别取 P,Q 两点,填写表格:
S1的值 S2的值 S1与S2的关系 猜想 S1,S2 与 k的关系
P (-1,4) Q (-2,2)
1
2
3
4
y
x
O
P
Q
S1
S2
P (-1,4)
Q (-2,2)
S1的值
S2的值
S1与S2的关系
S1,S2 与 k的关系
4
4
S1=S2
S1=S2=-k
2
1
-2
-1
-1
-2
3
4
若点 P 是 图象上的任意一点,作 PA 垂直于 x 轴,作 PB 垂直于 y 轴,则矩形 AOBP 的面积与 k 的关系是什么?
S矩形 AOBP=|k|,你能给出证明吗?
B
P
A
y
x
O
P
A
B
设点 P (a,b),∵点 P 在函数 的图象上,∴ ,即 ab=k.
∵S矩形 AOBP=PB·PA=|a|·|b|=|ab,
∴S矩形 AOBP=|k|.
反比例函数 (k≠0)中 k 的几何意义包括以下两种:
(2)如图,过双曲线上的任意一点 E 作 EF⊥y 轴,垂足为 F,连接EO,则S△EOF=.
B
P
A
y
x
O
P
A
B
(1)如图,过双曲线上任意一点 P(x,y)
分别作 x 轴、y 轴的垂线 PM,PN,
则S矩形 AOBP=|k|.
1.如图所示,点 A 是反比例函数图象上一点,过点 A 作 AB⊥y 轴于点 B,点 C,D 在 x 轴上,且 BC//AD,四边形 ABCD 的面积为 3,则这个反比例函数的解析式为 _______________.
A
B
C
D
O
E
y
x
新知探究
跟踪训练
S四边形ABOE =S四边形ABCD=3
|k|=3
图象在第二象限
k<0,x<0
(x<0 )
2.如图,点 A,B 是双曲线 上的点,分别过点 A,B作 x 轴的垂线段,垂足分别为 C,D,连接 OA,OB,若图中阴影部分的面积为1,则△OAE 与四边形 BECD 面积的和为 .
10
S△AOC= S△BOD =6
k=12
S阴影=1
S△OAE =5,
S四边形BECD =5
1.已知点 A(x1,3),B(x2,6)都在反比例函数 的图象上,则下列关系式一定正确的是( )
A.x1
随堂练习
在每一象限内,y 随 x 的增大而增大
2.如图所示,点 A 在双曲线 上,点 B 在双曲线 上,且 AB//x 轴,则△OAB 的面积= .
C
点 B在 上
S△OBC=4
S△AOC=
点 A 在 上
S△OAB=
3.如图,已知 A(-4,2),B(n,-4)两点是一次函数 y=kx+b 和反比例函数 图象的两个交点.
(1)求一次函数和反比例函数的解析式;
解:(1)∵A(-4,2)在 y= 上,
∴m=2×(-4)=-8,∴ B(2,-4).
把 A(-4,2)和 B(2,-4)的坐标分别代入 y=kx+b,
得 解得
∴一次函数、反比例函数的解析式分别为 y = -x-2,y= .
解:(2) y = -x-2中,令 y=0,则 x=-2,
即 C(-2,0),
所以 S△AOB=S△AOC+S△BOC= =6.
3.如图,已知 A(-4,2),B(n,-4)两点是一次函数 y=kx+b 和反比例函数 图象的两个交点.
(2)求△AOB 的面积;
解:(3)不等式 的解集,
即不等式 的解集,
由图可得,不等式 的解集为 x<-4或 0
(3)观察图象,直接写出不等式 的解集.
反比例函数
图象
性质
k 的几何意义
画法
形状
图象位置
增减性
列表、描点、连线
双曲线
课堂小结
对接中考
1.(2021 金华中考)已知点A(x1,y1),B(x2,y2)在反比例函数y=﹣ 的图象上.若x1<0<x2,则( )
A.y1<0<y2 B.y2<0<y1
C.y1<y2<0 D.y2<y1<0
解析:∵k=﹣12<0,∴双曲线在第二,四象限,∵x1<0<x2,∴点A在第二象限,点B在第四象限,∴y2<0<y1.
B
2.(2021 南京中考)如图,正比例函数y=kx与函数y= 的图象交于A,B两点,BC∥x轴,AC∥y轴,则S△ABC=__________.
解析:连接OC,设AC交x轴于点N,BC交y
轴于M点,∴S△AON=S△OBM =3.
12
N
M
∵BC∥x轴,AC∥y轴,∴S△AON=S△CON,S△OBM=S△OCM,
∴S△ABC=4S△AON=4× 3 =12.
3.(2021 苏州中考)如图,在平面直角坐标系中,四边形OABC为矩形,点C,A分别在x轴和y轴的正半轴上,点D为AB的中点.已知实数k≠0,一次函数y=﹣3x+k的图象经过点C,D,反比例函数y= (x>0)的图象经过点B,求k的值.
解:令y=0,则0=﹣3x+k,得x= ,∴C( ,0),
∴B( ,3).∵点D为AB的中点,∴D( ,3).
∵点D在直线y=﹣3x+k上,∴3=﹣3× +k,∴ k =6.
k
