5.1 平行四边形的性质 课件(共33张PPT)
文档属性
| 名称 | 5.1 平行四边形的性质 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 742.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-01 20:05:31 | ||
图片预览







文档简介
(共33张PPT)
第五章 平行四边形
1 平行四边形的性质
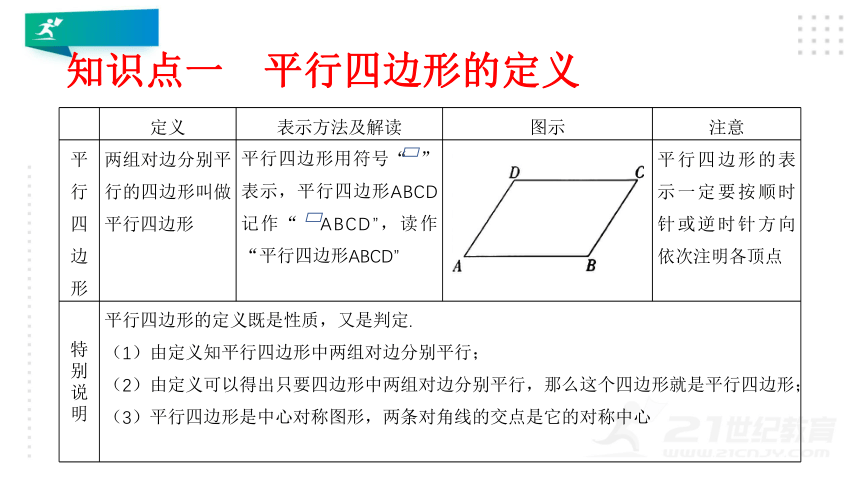
知识点一 平行四边形的定义
定义 表示方法及解读 图示 注意
平行四边形 两组对边分别平行的四边形叫做平行四边形 平行四边形用符号“ ”表示,平行四边形ABCD记作“ ABCD”,读作“平行四边形ABCD” 平行四边形的表示一定要按顺时针或逆时针方向依次注明各顶点
特 别 说 明 平行四边形的定义既是性质,又是判定. (1)由定义知平行四边形中两组对边分别平行; (2)由定义可以得出只要四边形中两组对边分别平行,那么这个四边形就是平行四边形; (3)平行四边形是中心对称图形,两条对角线的交点是它的对称中心
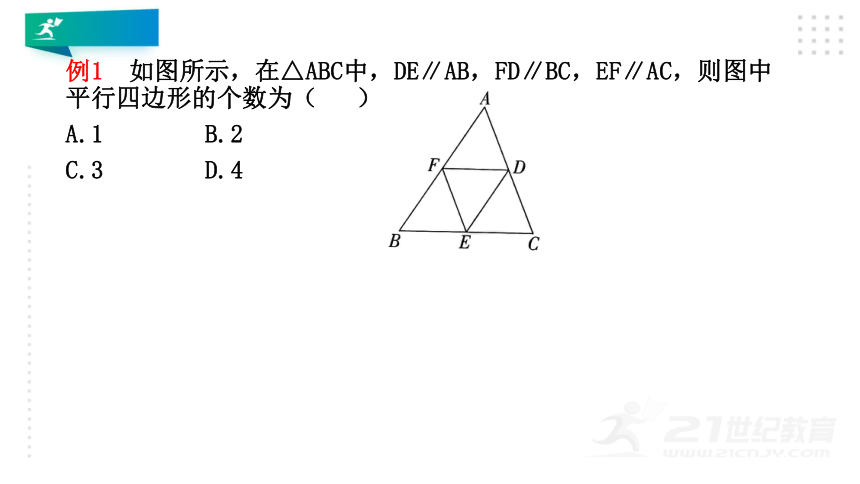
例1 如图所示,在△ABC中,DE∥AB,FD∥BC,EF∥AC,则图中平行四边形的个数为( )
A.1 B.2
C.3 D.4
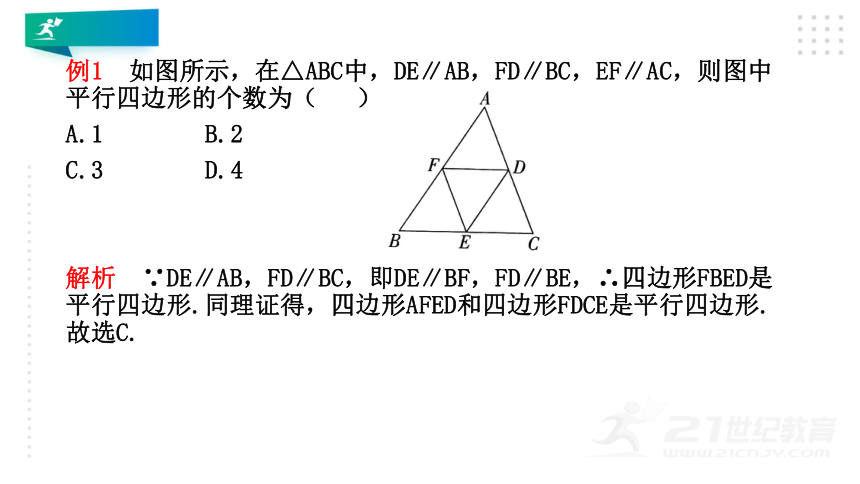
例1 如图所示,在△ABC中,DE∥AB,FD∥BC,EF∥AC,则图中平行四边形的个数为( )
A.1 B.2
C.3 D.4
解析 ∵DE∥AB,FD∥BC,即DE∥BF,FD∥BE,∴四边形FBED是平行四边形.同理证得,四边形AFED和四边形FDCE是平行四边形.故选C.
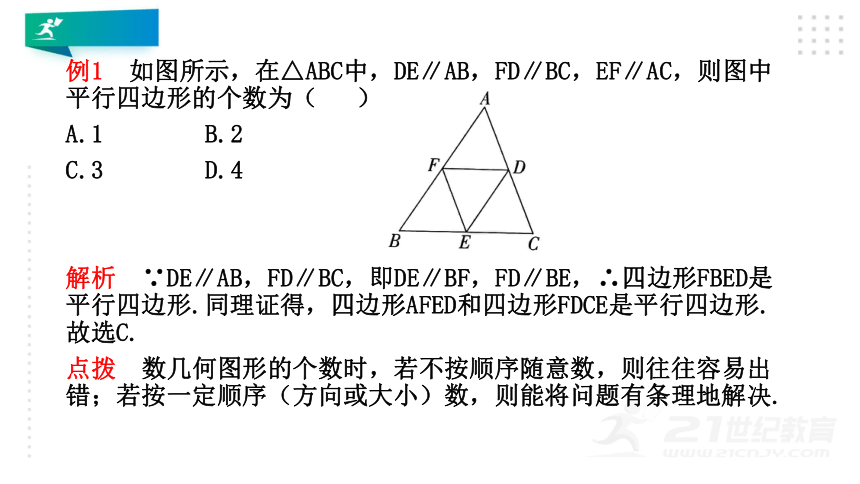
例1 如图所示,在△ABC中,DE∥AB,FD∥BC,EF∥AC,则图中平行四边形的个数为( )
A.1 B.2
C.3 D.4
解析 ∵DE∥AB,FD∥BC,即DE∥BF,FD∥BE,∴四边形FBED是平行四边形.同理证得,四边形AFED和四边形FDCE是平行四边形.故选C.
点拨 数几何图形的个数时,若不按顺序随意数,则往往容易出错;若按一定顺序(方向或大小)数,则能将问题有条理地解决.
知识点二 平行四边形的性质
类别 文字语言 数学语言 图示
边 平行四边形的对边相等 在 ABCD中,AB=CD,AD=BC
角 平行四边形的对角相等 在ABCD中,∠ABC=∠CDA,∠BCD=∠DAB
对角线 平行四边形的对角线互相平分 在 ABCD中,OA=OC,OB=OD
对称性 平行四边形是中心对称图形,两条对角线的交点是它的对称中心
知识点二 平行四边形的性质
特别提醒
(1)平行四边形的邻角互补.
(2)平行四边形的每条对角线都将平行四边形分为两个全等的三角形
(3)平行四边形中,被两条对角线分成的四个三角形的面积相等.
例2 (1)在平行四边形ABCD中,若∠A:∠B=5:4,求∠C的度数;
(2)平行四边形ABCD的周长为28cm,AB:BC=3:4,求它的各边长.
解析 (1)设∠A=5x°(x>0),则∠B=4x°,
∵四边形ABCD是平行四边形,∴∠A=∠C,∠A+∠B=180°,
即5x°+4x°=180°,∴x=20,∴∠A=100°,∠B=80°,
则∠C=∠A=100°.
(2)∵四边形ABCD是平行四边形,∴AB=CD,BC=AD.
又∵AB+BC+CD+AD=28cm,∴AB+BC=14cm.
设AB、BC的长分别为3ycm、4ycm(y>0),
则3y+4y=14,∴y=2.
∴AB=CD=6 cm,BC=AD=8 cm.
点拨 有关平行四边形的边、角、对角线的计算问题,常常利用平行四边形的对边相等、对角相等、邻角互补、对角线互相平分等性质解决.
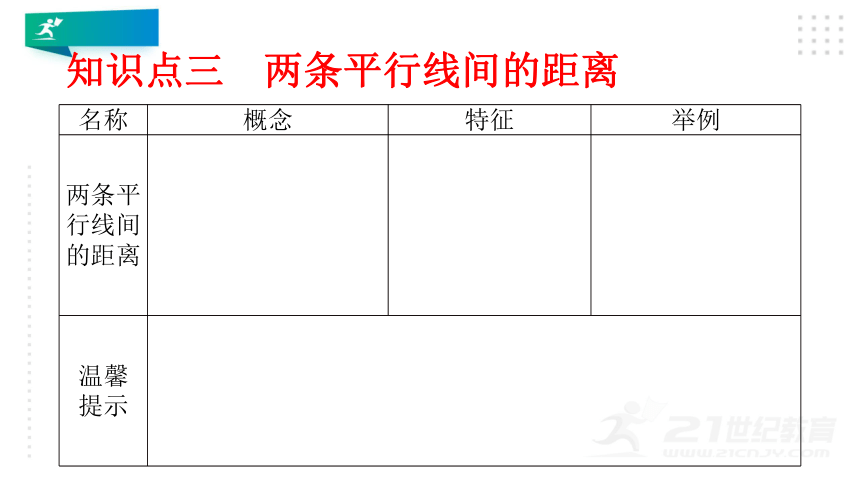
知识点三 两条平行线间的距离
名称 概念 特征 举例
两条平行线间的距离
温馨 提示 知识点三 两条平行线间的距离
名称 概念 特征 举例
两条平行线间的距离 如果两条直线互相平行,那么其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离
温馨 提示 知识点三 两条平行线间的距离
名称 概念 特征 举例
两条平行线间的距离 如果两条直线互相平行,那么其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离 两条平行线中,一条直线上任意两点到另一条直线的距离相等,即两平行线间的距离处处相等
温馨 提示 知识点三 两条平行线间的距离
名称 概念 特征 举例
两条平行线间的距离 如果两条直线互相平行,那么其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离 两条平行线中,一条直线上任意两点到另一条直线的距离相等,即两平行线间的距离处处相等 a∥b,AB⊥b于点B,MN⊥b于点N,则AB=MN
温馨 提示 知识点三 两条平行线间的距离
名称 概念 特征 举例
两条平行线间的距离 如果两条直线互相平行,那么其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离 两条平行线中,一条直线上任意两点到另一条直线的距离相等,即两平行线间的距离处处相等 a∥b,AB⊥b于点B,MN⊥b于点N,则AB=MN
温馨 提示 (1)两条平行线间的距离是指垂线段的长度,是正值;(2)平行线的位置确定后,它们之间的距离是定值,不随垂线段位置的改变而改变; (3)两条平行线间的距离处处相等,因此在作平行四边形的高时,可根据条件灵活选择位置. 例3 如图所示,l1∥l2,BE∥CF,BA⊥l1于点A,CD⊥l1于点D,下面的四个结论:①AB=DC;②BE=CF;③S△ABE=S△DCF;④S四边形ABCD=S四边形BCFE,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
解析 ∵夹在两平行线间的平行线段的长度相等,
∴①②中的结论正确;
由题意得四边形ABCD,四边形BCFE是平行四边形.
∵ S平行四边形ABCD=AB·BC, S平行四边形BCFE=BC·CD,AB=CD,
∴S平行四边形ABCD=S平行四边形BCFE,∴④中的结论正确;
∵s△ABE=S平行四边形ABCD-S四边形BCDE,S△DCF=S平行四边形BCFE-S四边形BCDE.
∴S△ABE=S△DCF,∴③中的结论正确.故选A.
点拨 平行线间的距离相等这一性质通常应用在证明两个三角形面积相等的问题上当两个三角形具备等底等高时,两个三角形的面积相等.
经典例题
题型一 运用平行四边形的性质求角的度数
例1 如图所示,在平行四边形ABCD中,∠B=110°,延长AD至F点,延长CD至E点,连接EF,求∠E+∠F的度数.
题型一 运用平行四边形的性质求角的度数
例1 如图所示,在平行四边形ABCD中,∠B=110°,延长AD至F点,延长CD至E点,连接EF,求∠E+∠F的度数.
分析 利用平行四边形的对角相等得出∠ADC=∠B=110°,进而利用三角形内角和定理得出答案.
解析 ∵四边形ABCD是平行四边形,∴∠ADC=∠B=110°
又∵∠EDF=∠ADC=110°(对顶角相等),
∴在△EDF中,∠E+∠F=180°-110°=70°.
解析 ∵四边形ABCD是平行四边形,∴∠ADC=∠B=110°
又∵∠EDF=∠ADC=110°(对顶角相等),
∴在△EDF中,∠E+∠F=180°-110°=70°.
点拨 计算与平行四边形有关的角度问题时,可以利用平行四边形的对角相等、邻角互补等知识来解决.
题型二 运用平行四边形的性质求边长
例2 如图所示,平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为( )
A.8 B.10 C.12 D.14
题型二 运用平行四边形的性质求边长
解析 ∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,∴∠AFB=∠FBC.
∵BF平分∠ABC,∴∠ABF=∠FBC,则∠ABF=∠AFB,∴AF=AB=6,
∵CE平分∠BCD,∴∠BCE=∠ECD.
又∵AD∥BC,∴∠CED=∠ECB,∴∠DEC=∠DCE,∴DE=DC=6.
又∵AD=AF+DE-EF,即AD=6+6-2=10,∴BC=AD=10.
题型二 运用平行四边形的性质求边长
解析 ∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,∴∠AFB=∠FBC.
∵BF平分∠ABC,∴∠ABF=∠FBC,则∠ABF=∠AFB,∴AF=AB=6,
∵CE平分∠BCD,∴∠BCE=∠ECD.
又∵AD∥BC,∴∠CED=∠ECB,∴∠DEC=∠DCE,∴DE=DC=6.
又∵AD=AF+DE-EF,即AD=6+6-2=10,∴BC=AD=10.
点拨 利用平行四边形的性质求线段的长度、角的度数时,一定要抓住平行四边形的性质中边、角之间的相等关系.题型三应用平行四边形的性质解决几何证明问题.
例3 如图所示,在平行四边形ABCD中,点E、F在对角线BD上,BE=DF,点M、N在BA、DC的延长线上,AM=CN,连接ME、NF试判断线段ME与NF的关系,并说明理由.
例3 如图所示,在平行四边形ABCD中,点E、F在对角线BD上,BE=DF,点M、N在BA、DC的延长线上,AM=CN,连接ME、NF试判断线段ME与NF的关系,并说明理由.
分析 利用SAS证得△BME≌△DNF后即可得出结论.
解析 ME=NF且ME∥NF
理由:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∴∠EBM=∠FDN,∵AM=CN,∴MB=ND.
∵BE=DF,∴BE+EF=DF+EF,即BF=DE.
∵在△BME和△DNF中,∴△BME≌△DNF(SAS),
∴ME=NF,∠MEB=∠NFD,∴∠MEF=∠BFN.∴ME∥NF.
故ME与NF的关系是ME=NF且ME∥NF.
解析 ME=NF且ME∥NF
理由:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∴∠EBM=∠FDN,∵AM=CN,∴MB=ND.
∵BE=DF,∴BE+EF=DF+EF,即BF=DE.
∵在△BME和△DNF中,∴△BME≌△DNF(SAS),
∴ME=NF,∠MEB=∠NFD,∴∠MEF=∠BFN.∴ME∥NF.
故ME与NF的关系是ME=NF且ME∥NF.
点拨 利用平行四边形的性质求相等的线段、相等的角,是除利用全等三角形、等腰三角形之外的又一重要性质.
第五章 平行四边形
1 平行四边形的性质
知识点一 平行四边形的定义
定义 表示方法及解读 图示 注意
平行四边形 两组对边分别平行的四边形叫做平行四边形 平行四边形用符号“ ”表示,平行四边形ABCD记作“ ABCD”,读作“平行四边形ABCD” 平行四边形的表示一定要按顺时针或逆时针方向依次注明各顶点
特 别 说 明 平行四边形的定义既是性质,又是判定. (1)由定义知平行四边形中两组对边分别平行; (2)由定义可以得出只要四边形中两组对边分别平行,那么这个四边形就是平行四边形; (3)平行四边形是中心对称图形,两条对角线的交点是它的对称中心
例1 如图所示,在△ABC中,DE∥AB,FD∥BC,EF∥AC,则图中平行四边形的个数为( )
A.1 B.2
C.3 D.4
例1 如图所示,在△ABC中,DE∥AB,FD∥BC,EF∥AC,则图中平行四边形的个数为( )
A.1 B.2
C.3 D.4
解析 ∵DE∥AB,FD∥BC,即DE∥BF,FD∥BE,∴四边形FBED是平行四边形.同理证得,四边形AFED和四边形FDCE是平行四边形.故选C.
例1 如图所示,在△ABC中,DE∥AB,FD∥BC,EF∥AC,则图中平行四边形的个数为( )
A.1 B.2
C.3 D.4
解析 ∵DE∥AB,FD∥BC,即DE∥BF,FD∥BE,∴四边形FBED是平行四边形.同理证得,四边形AFED和四边形FDCE是平行四边形.故选C.
点拨 数几何图形的个数时,若不按顺序随意数,则往往容易出错;若按一定顺序(方向或大小)数,则能将问题有条理地解决.
知识点二 平行四边形的性质
类别 文字语言 数学语言 图示
边 平行四边形的对边相等 在 ABCD中,AB=CD,AD=BC
角 平行四边形的对角相等 在ABCD中,∠ABC=∠CDA,∠BCD=∠DAB
对角线 平行四边形的对角线互相平分 在 ABCD中,OA=OC,OB=OD
对称性 平行四边形是中心对称图形,两条对角线的交点是它的对称中心
知识点二 平行四边形的性质
特别提醒
(1)平行四边形的邻角互补.
(2)平行四边形的每条对角线都将平行四边形分为两个全等的三角形
(3)平行四边形中,被两条对角线分成的四个三角形的面积相等.
例2 (1)在平行四边形ABCD中,若∠A:∠B=5:4,求∠C的度数;
(2)平行四边形ABCD的周长为28cm,AB:BC=3:4,求它的各边长.
解析 (1)设∠A=5x°(x>0),则∠B=4x°,
∵四边形ABCD是平行四边形,∴∠A=∠C,∠A+∠B=180°,
即5x°+4x°=180°,∴x=20,∴∠A=100°,∠B=80°,
则∠C=∠A=100°.
(2)∵四边形ABCD是平行四边形,∴AB=CD,BC=AD.
又∵AB+BC+CD+AD=28cm,∴AB+BC=14cm.
设AB、BC的长分别为3ycm、4ycm(y>0),
则3y+4y=14,∴y=2.
∴AB=CD=6 cm,BC=AD=8 cm.
点拨 有关平行四边形的边、角、对角线的计算问题,常常利用平行四边形的对边相等、对角相等、邻角互补、对角线互相平分等性质解决.
知识点三 两条平行线间的距离
名称 概念 特征 举例
两条平行线间的距离
温馨 提示 知识点三 两条平行线间的距离
名称 概念 特征 举例
两条平行线间的距离 如果两条直线互相平行,那么其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离
温馨 提示 知识点三 两条平行线间的距离
名称 概念 特征 举例
两条平行线间的距离 如果两条直线互相平行,那么其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离 两条平行线中,一条直线上任意两点到另一条直线的距离相等,即两平行线间的距离处处相等
温馨 提示 知识点三 两条平行线间的距离
名称 概念 特征 举例
两条平行线间的距离 如果两条直线互相平行,那么其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离 两条平行线中,一条直线上任意两点到另一条直线的距离相等,即两平行线间的距离处处相等 a∥b,AB⊥b于点B,MN⊥b于点N,则AB=MN
温馨 提示 知识点三 两条平行线间的距离
名称 概念 特征 举例
两条平行线间的距离 如果两条直线互相平行,那么其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离 两条平行线中,一条直线上任意两点到另一条直线的距离相等,即两平行线间的距离处处相等 a∥b,AB⊥b于点B,MN⊥b于点N,则AB=MN
温馨 提示 (1)两条平行线间的距离是指垂线段的长度,是正值;(2)平行线的位置确定后,它们之间的距离是定值,不随垂线段位置的改变而改变; (3)两条平行线间的距离处处相等,因此在作平行四边形的高时,可根据条件灵活选择位置. 例3 如图所示,l1∥l2,BE∥CF,BA⊥l1于点A,CD⊥l1于点D,下面的四个结论:①AB=DC;②BE=CF;③S△ABE=S△DCF;④S四边形ABCD=S四边形BCFE,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
解析 ∵夹在两平行线间的平行线段的长度相等,
∴①②中的结论正确;
由题意得四边形ABCD,四边形BCFE是平行四边形.
∵ S平行四边形ABCD=AB·BC, S平行四边形BCFE=BC·CD,AB=CD,
∴S平行四边形ABCD=S平行四边形BCFE,∴④中的结论正确;
∵s△ABE=S平行四边形ABCD-S四边形BCDE,S△DCF=S平行四边形BCFE-S四边形BCDE.
∴S△ABE=S△DCF,∴③中的结论正确.故选A.
点拨 平行线间的距离相等这一性质通常应用在证明两个三角形面积相等的问题上当两个三角形具备等底等高时,两个三角形的面积相等.
经典例题
题型一 运用平行四边形的性质求角的度数
例1 如图所示,在平行四边形ABCD中,∠B=110°,延长AD至F点,延长CD至E点,连接EF,求∠E+∠F的度数.
题型一 运用平行四边形的性质求角的度数
例1 如图所示,在平行四边形ABCD中,∠B=110°,延长AD至F点,延长CD至E点,连接EF,求∠E+∠F的度数.
分析 利用平行四边形的对角相等得出∠ADC=∠B=110°,进而利用三角形内角和定理得出答案.
解析 ∵四边形ABCD是平行四边形,∴∠ADC=∠B=110°
又∵∠EDF=∠ADC=110°(对顶角相等),
∴在△EDF中,∠E+∠F=180°-110°=70°.
解析 ∵四边形ABCD是平行四边形,∴∠ADC=∠B=110°
又∵∠EDF=∠ADC=110°(对顶角相等),
∴在△EDF中,∠E+∠F=180°-110°=70°.
点拨 计算与平行四边形有关的角度问题时,可以利用平行四边形的对角相等、邻角互补等知识来解决.
题型二 运用平行四边形的性质求边长
例2 如图所示,平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为( )
A.8 B.10 C.12 D.14
题型二 运用平行四边形的性质求边长
解析 ∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,∴∠AFB=∠FBC.
∵BF平分∠ABC,∴∠ABF=∠FBC,则∠ABF=∠AFB,∴AF=AB=6,
∵CE平分∠BCD,∴∠BCE=∠ECD.
又∵AD∥BC,∴∠CED=∠ECB,∴∠DEC=∠DCE,∴DE=DC=6.
又∵AD=AF+DE-EF,即AD=6+6-2=10,∴BC=AD=10.
题型二 运用平行四边形的性质求边长
解析 ∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,∴∠AFB=∠FBC.
∵BF平分∠ABC,∴∠ABF=∠FBC,则∠ABF=∠AFB,∴AF=AB=6,
∵CE平分∠BCD,∴∠BCE=∠ECD.
又∵AD∥BC,∴∠CED=∠ECB,∴∠DEC=∠DCE,∴DE=DC=6.
又∵AD=AF+DE-EF,即AD=6+6-2=10,∴BC=AD=10.
点拨 利用平行四边形的性质求线段的长度、角的度数时,一定要抓住平行四边形的性质中边、角之间的相等关系.题型三应用平行四边形的性质解决几何证明问题.
例3 如图所示,在平行四边形ABCD中,点E、F在对角线BD上,BE=DF,点M、N在BA、DC的延长线上,AM=CN,连接ME、NF试判断线段ME与NF的关系,并说明理由.
例3 如图所示,在平行四边形ABCD中,点E、F在对角线BD上,BE=DF,点M、N在BA、DC的延长线上,AM=CN,连接ME、NF试判断线段ME与NF的关系,并说明理由.
分析 利用SAS证得△BME≌△DNF后即可得出结论.
解析 ME=NF且ME∥NF
理由:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∴∠EBM=∠FDN,∵AM=CN,∴MB=ND.
∵BE=DF,∴BE+EF=DF+EF,即BF=DE.
∵在△BME和△DNF中,∴△BME≌△DNF(SAS),
∴ME=NF,∠MEB=∠NFD,∴∠MEF=∠BFN.∴ME∥NF.
故ME与NF的关系是ME=NF且ME∥NF.
解析 ME=NF且ME∥NF
理由:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∴∠EBM=∠FDN,∵AM=CN,∴MB=ND.
∵BE=DF,∴BE+EF=DF+EF,即BF=DE.
∵在△BME和△DNF中,∴△BME≌△DNF(SAS),
∴ME=NF,∠MEB=∠NFD,∴∠MEF=∠BFN.∴ME∥NF.
故ME与NF的关系是ME=NF且ME∥NF.
点拨 利用平行四边形的性质求相等的线段、相等的角,是除利用全等三角形、等腰三角形之外的又一重要性质.
