2021--2022学年北师大版九年级数学下册3.2 圆的对称性 课件(共17张PPT)
文档属性
| 名称 | 2021--2022学年北师大版九年级数学下册3.2 圆的对称性 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 08:52:48 | ||
图片预览





文档简介
(共17张PPT)
圆的对称性
3.2
学习目标
1. 掌握圆的轴对称性和中心对称性。
2. 掌握圆心角的概念。
掌握在同圆或等圆中,圆心角、弦、弧中
有一个量相等就可以推出其他的两个量
对应相等,以及它们在解题中的应用。
3.我们所学过的图形中,哪些图形既是轴对称图形又是中心对称图形?
2.什么是中心对称图形?我们学过哪些中心对称图形?
在平面内,如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形。
1.什么是轴对称图形?我们学过哪些轴对称图形?
在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
线段、矩形、正方形、角、菱形、等腰三角形
线段、矩形、正方形、菱形、平行四边形
线段、矩形、正方形、菱形
复习提问:
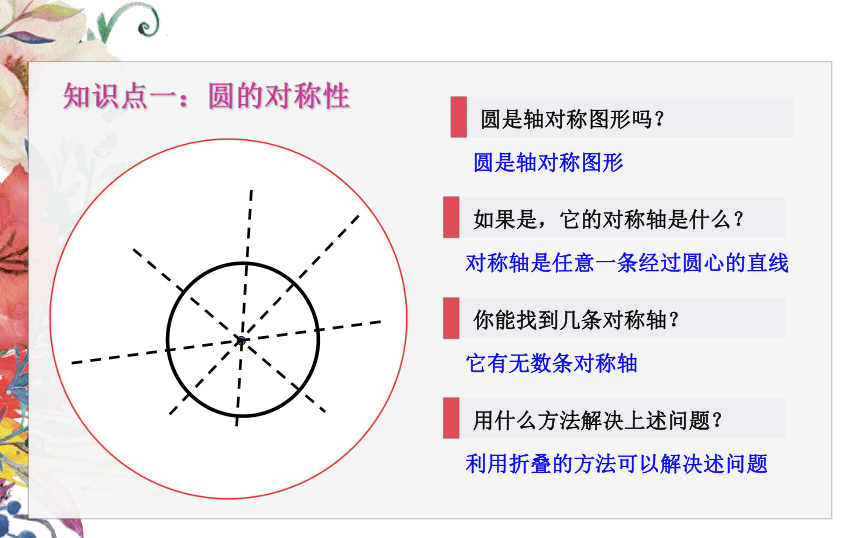
知识点一:圆的对称性
圆是轴对称图形吗?
圆是轴对称图形
如果是,它的对称轴是什么?
对称轴是任意一条经过圆心的直线
你能找到几条对称轴?
它有无数条对称轴
用什么方法解决上述问题?
利用折叠的方法可以解决述问题
一个圆绕着它的圆心旋转180°,还能与原来的图形的重合?圆是中心对称图形吗?如果是,它的对称中心是什么?
圆是中心对称图形,其对称中心就是圆心。
若旋转角度不是180°,而是旋转任意角度,则旋转过后的图形能与原图形重合吗?
圆具有旋转不变性。
圆的对称性:
1、圆是轴对称图形,有无数条对称轴,其对称轴是任意一条过圆心的直线。
2、圆是中心对称图形,对称中心是圆心。
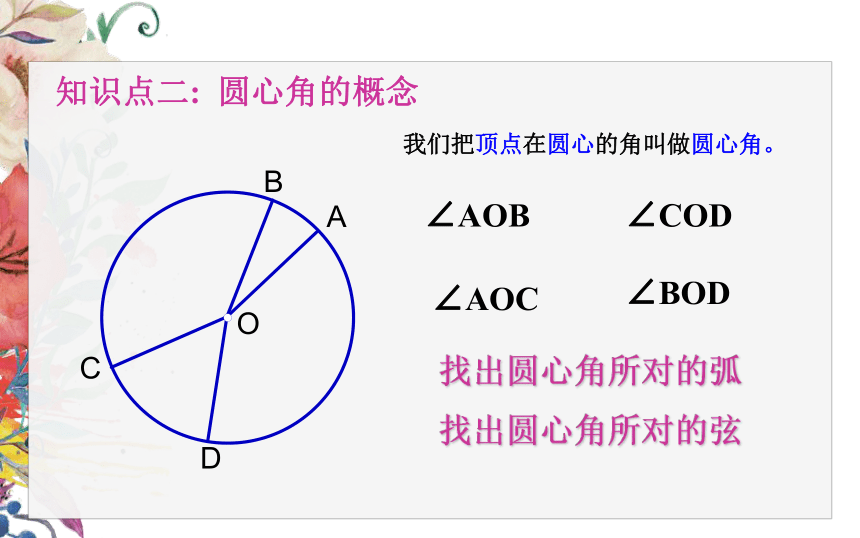
知识点二: 圆心角的概念
∠AOB
∠COD
∠AOC
∠BOD
我们把顶点在圆心的角叫做圆心角。
找出圆心角所对的弧
找出圆心角所对的弦
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
知识点三: 圆心角、弧、弦之间的关系
1、在等圆⊙O和⊙O′中,分别作相等的圆心角 ∠AOB和∠A′O′B′,将两圆重合,并使OA和O′A′重合,你能找到哪些相等的量?
A
B
O
A′
B′
O′
2、在同圆⊙O中,分别作相等的圆心角 ∠AOB和∠A′OB′,绕点O旋转∠AOB使OA和OA′重合,你能找到哪些相等的量?
定理:在同圆或等圆中,相等的圆心角所对的弧,所对的弦相等。
·
O
A
B
A′
B′
想一想:
1、在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗 你是怎么想的?
2、在同圆或等到圆中,如果两条弦相等,你能得出什么结论?你是怎么想的?
定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
A
B
O
B′
A′
O′
1、如图,AB、CD是⊙O的两条弦。
(1)如果AB=CD,那么___________,_____________。
(2)如果 ,那么___________,_____________。
(3)如果∠AOB=∠COD,那么__________,_________ 。
AB= CD
⌒ ⌒
AB= CD
⌒ ⌒
AB=CD
AB=CD
AB= CD
⌒ ⌒
∠AOB=∠COD
∠AOB=∠COD
随堂练习:
O
A
B
C
D
B
E
O
D
A
C
知识技能1:
O
B
C
A
知识技能2:
2.如图,A、B、C、D是⊙O上的四点,AB=DC,△ABC与△DCB全等吗?为什么?
O
B
A
D
C
课 堂 小 结
本节课你的收获是什么?
圆的对称性
3.2
学习目标
1. 掌握圆的轴对称性和中心对称性。
2. 掌握圆心角的概念。
掌握在同圆或等圆中,圆心角、弦、弧中
有一个量相等就可以推出其他的两个量
对应相等,以及它们在解题中的应用。
3.我们所学过的图形中,哪些图形既是轴对称图形又是中心对称图形?
2.什么是中心对称图形?我们学过哪些中心对称图形?
在平面内,如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形。
1.什么是轴对称图形?我们学过哪些轴对称图形?
在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
线段、矩形、正方形、角、菱形、等腰三角形
线段、矩形、正方形、菱形、平行四边形
线段、矩形、正方形、菱形
复习提问:
知识点一:圆的对称性
圆是轴对称图形吗?
圆是轴对称图形
如果是,它的对称轴是什么?
对称轴是任意一条经过圆心的直线
你能找到几条对称轴?
它有无数条对称轴
用什么方法解决上述问题?
利用折叠的方法可以解决述问题
一个圆绕着它的圆心旋转180°,还能与原来的图形的重合?圆是中心对称图形吗?如果是,它的对称中心是什么?
圆是中心对称图形,其对称中心就是圆心。
若旋转角度不是180°,而是旋转任意角度,则旋转过后的图形能与原图形重合吗?
圆具有旋转不变性。
圆的对称性:
1、圆是轴对称图形,有无数条对称轴,其对称轴是任意一条过圆心的直线。
2、圆是中心对称图形,对称中心是圆心。
知识点二: 圆心角的概念
∠AOB
∠COD
∠AOC
∠BOD
我们把顶点在圆心的角叫做圆心角。
找出圆心角所对的弧
找出圆心角所对的弦
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
知识点三: 圆心角、弧、弦之间的关系
1、在等圆⊙O和⊙O′中,分别作相等的圆心角 ∠AOB和∠A′O′B′,将两圆重合,并使OA和O′A′重合,你能找到哪些相等的量?
A
B
O
A′
B′
O′
2、在同圆⊙O中,分别作相等的圆心角 ∠AOB和∠A′OB′,绕点O旋转∠AOB使OA和OA′重合,你能找到哪些相等的量?
定理:在同圆或等圆中,相等的圆心角所对的弧,所对的弦相等。
·
O
A
B
A′
B′
想一想:
1、在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗 你是怎么想的?
2、在同圆或等到圆中,如果两条弦相等,你能得出什么结论?你是怎么想的?
定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
A
B
O
B′
A′
O′
1、如图,AB、CD是⊙O的两条弦。
(1)如果AB=CD,那么___________,_____________。
(2)如果 ,那么___________,_____________。
(3)如果∠AOB=∠COD,那么__________,_________ 。
AB= CD
⌒ ⌒
AB= CD
⌒ ⌒
AB=CD
AB=CD
AB= CD
⌒ ⌒
∠AOB=∠COD
∠AOB=∠COD
随堂练习:
O
A
B
C
D
B
E
O
D
A
C
知识技能1:
O
B
C
A
知识技能2:
2.如图,A、B、C、D是⊙O上的四点,AB=DC,△ABC与△DCB全等吗?为什么?
O
B
A
D
C
课 堂 小 结
本节课你的收获是什么?
