1.2.3 相反数
图片预览






文档简介
(共14张PPT)
⑴数轴上与原点距离是2 的点有____个,这些点表示的数是_____;与原点的距离是5 的点有_____个,这些点表示的数是____。
2
2或-2
2
5或-5
(2)一般地,设a是一个正数,数轴上与原点的距离是a的点有____个,它们分别在原点的_____,表示______.
2
左右
a 或 -a
你觉得这两对数又有哪些相同,哪些不同呢?
-1.5 +1.5
数值相同
符号不同
1.定义:像-3和3,-1.5和1.5这样,只有符号不同的两个数叫做互为相反数。
例如:3的相反数是 ,-3的相反数是 ; 是1.5的相反数, 是-1.5的相反数. -2b的相反数是
-3
3
-1.5
1.5
一般地,数a的相反数是-a,a可以是正数、负数或0。
求一个数的相反数即在这个数的前面加上“—”号。
规定:0的相反数是0, 即-0=0.
2b
0
1
4
-4
-2.5
2.5
4
4
2.5
2.5
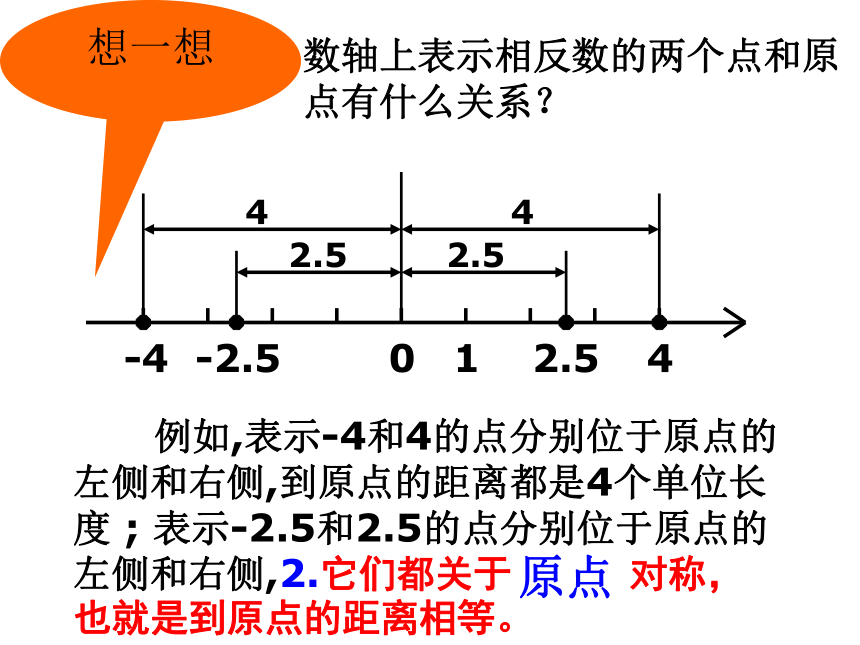
例如,表示-4和4的点分别位于原点的左侧和右侧,到原点的距离都是4个单位长度 ; 表示-2.5和2.5的点分别位于原点的左侧和右侧,2.它们都关于 对称,也就是到原点的距离相等。
想一想
数轴上表示相反数的两个点和原点有什么关系?
原点
判断题
1.两个符号相反的数叫做相反数.( )
2. 只有0的相反数是它本身.( )
3.一个数的相反数一定是负数.( )
4.数轴上位于原点的两侧且到原点的距离相等的两点所表示的两个数互为相反数.( )
5.具有相反意义的量的两个数互为相反数.( )
6.-8是相反数.( )
√
×
×
×
×
√
化简下列各数的符号
(1)-(-3)
(2)-(+5)
(3)+(+2)
(4)-[+(-2)]
(5)-[-(-1)]
(6)-{+[-(+4)]}
(7)-{-{-[-(-6)]}}
你发现什么规律了吗?
3.有奇数个负号的最后得数为负,有偶数个负号的最后得数为正。简称:奇负偶正
4.若两个数a、b互为相反数,就可得到a+b=0;反过来,若a+b=0,则a、b互为相反数.
例1:若a、b互为相反数,c、d 互为倒数,则a +b +cd +1= .
2
2.已知数轴上A、B两点互为相反数,它们分别表示为m ,n(m>n),并且A、B两点间的距离是6,则m= , n= .
1. a-3的相反数可表示为 .
m+n的相反数可表示为 .
2.若a-1与-3互为相反数,则a的
值为 .
拓广探究
4
-(m+n)
3.一个数的相反数是非负数,那么这个数是 ( )
A.0 B.负数 C.非正数 D.正数
巩固练习
4.下面各组数,互为相反数的有 ( )
;-(-8)与-(+8);
;-1.5与 .
A.1组 B.2组 C.3组 D.4组
C
B
5.若 是负数,则- 是 数;
若 - 是负数,则 是 数.
巩固练习
13.4和-13.4
6.数轴上表示互为相反数的两个点之间的距离为
26.8,则这两个数是 .
正
正
3、下面我们思考一些问题: (1)正数的相反数是什么数?
(2)负数的相反数是什么数? (3)0 的相反数是什么?
(4)什么数的相反数小于它本身? (5)什么数的相反数大于它本身? (6)什么数的相反数等于它本身?
畅谈所得 感悟提升
这节课你学到了哪些知识?
1.只有符号不同的两个数叫做互为相反数。
2.数a的相反数是-a,a可以是正数、负数或0. 规定:0的相反数是0。
4.数轴上表示相反数的两个点位于原点的两侧,到原点的距离相等,并且关于原点对称。
3.求一个数的相反数即在这个数的前面加上“-”
5.对于多重符号的化简,可根据“-”号的个数确定. 如果“-”号是奇数个,结果为负;如果“-”号是偶数个,结果为正。
4.如果a、b互为相反数,则a +b=0,反之,若a +b=0,则a、b互为相反数.
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
⑴数轴上与原点距离是2 的点有____个,这些点表示的数是_____;与原点的距离是5 的点有_____个,这些点表示的数是____。
2
2或-2
2
5或-5
(2)一般地,设a是一个正数,数轴上与原点的距离是a的点有____个,它们分别在原点的_____,表示______.
2
左右
a 或 -a
你觉得这两对数又有哪些相同,哪些不同呢?
-1.5 +1.5
数值相同
符号不同
1.定义:像-3和3,-1.5和1.5这样,只有符号不同的两个数叫做互为相反数。
例如:3的相反数是 ,-3的相反数是 ; 是1.5的相反数, 是-1.5的相反数. -2b的相反数是
-3
3
-1.5
1.5
一般地,数a的相反数是-a,a可以是正数、负数或0。
求一个数的相反数即在这个数的前面加上“—”号。
规定:0的相反数是0, 即-0=0.
2b
0
1
4
-4
-2.5
2.5
4
4
2.5
2.5
例如,表示-4和4的点分别位于原点的左侧和右侧,到原点的距离都是4个单位长度 ; 表示-2.5和2.5的点分别位于原点的左侧和右侧,2.它们都关于 对称,也就是到原点的距离相等。
想一想
数轴上表示相反数的两个点和原点有什么关系?
原点
判断题
1.两个符号相反的数叫做相反数.( )
2. 只有0的相反数是它本身.( )
3.一个数的相反数一定是负数.( )
4.数轴上位于原点的两侧且到原点的距离相等的两点所表示的两个数互为相反数.( )
5.具有相反意义的量的两个数互为相反数.( )
6.-8是相反数.( )
√
×
×
×
×
√
化简下列各数的符号
(1)-(-3)
(2)-(+5)
(3)+(+2)
(4)-[+(-2)]
(5)-[-(-1)]
(6)-{+[-(+4)]}
(7)-{-{-[-(-6)]}}
你发现什么规律了吗?
3.有奇数个负号的最后得数为负,有偶数个负号的最后得数为正。简称:奇负偶正
4.若两个数a、b互为相反数,就可得到a+b=0;反过来,若a+b=0,则a、b互为相反数.
例1:若a、b互为相反数,c、d 互为倒数,则a +b +cd +1= .
2
2.已知数轴上A、B两点互为相反数,它们分别表示为m ,n(m>n),并且A、B两点间的距离是6,则m= , n= .
1. a-3的相反数可表示为 .
m+n的相反数可表示为 .
2.若a-1与-3互为相反数,则a的
值为 .
拓广探究
4
-(m+n)
3.一个数的相反数是非负数,那么这个数是 ( )
A.0 B.负数 C.非正数 D.正数
巩固练习
4.下面各组数,互为相反数的有 ( )
;-(-8)与-(+8);
;-1.5与 .
A.1组 B.2组 C.3组 D.4组
C
B
5.若 是负数,则- 是 数;
若 - 是负数,则 是 数.
巩固练习
13.4和-13.4
6.数轴上表示互为相反数的两个点之间的距离为
26.8,则这两个数是 .
正
正
3、下面我们思考一些问题: (1)正数的相反数是什么数?
(2)负数的相反数是什么数? (3)0 的相反数是什么?
(4)什么数的相反数小于它本身? (5)什么数的相反数大于它本身? (6)什么数的相反数等于它本身?
畅谈所得 感悟提升
这节课你学到了哪些知识?
1.只有符号不同的两个数叫做互为相反数。
2.数a的相反数是-a,a可以是正数、负数或0. 规定:0的相反数是0。
4.数轴上表示相反数的两个点位于原点的两侧,到原点的距离相等,并且关于原点对称。
3.求一个数的相反数即在这个数的前面加上“-”
5.对于多重符号的化简,可根据“-”号的个数确定. 如果“-”号是奇数个,结果为负;如果“-”号是偶数个,结果为正。
4.如果a、b互为相反数,则a +b=0,反之,若a +b=0,则a、b互为相反数.
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
