3.2 用频率估计概率 课件(共27张PPT)
文档属性
| 名称 | 3.2 用频率估计概率 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 819.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 06:49:23 | ||
图片预览





文档简介
(共27张PPT)
3.2 用频率估计概率
第三章
概率的进一步认识
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.理解试验次数较大时试验频率趋于稳定这一规律;2.结合具体情境掌握如何用频率估计概率;
3.通过概率计算进一步比较概率与频率之间的关系.
导入新课
1.复习回顾
概率:事件发生的可能性的大小
频数:在实验中,每个对象出现的次数
频率:所考察对象出现的次数与实验的总次数的比
频率=
可能发生的总结果数
用列举法求概率的条件是什么
(1)实验的所有结果是有限个
(2)各种结果的可能性相等.
A可能发生的结果数
导入新课
1
2
在纸箱里面,共放置10颗球,其中3个红球,7个黑球。摸出红球的概率是多少?
在实际摸球中,摸10次一定摸到3次红球吗?你还会发现什么?
用频率估计概率
掷硬币试验
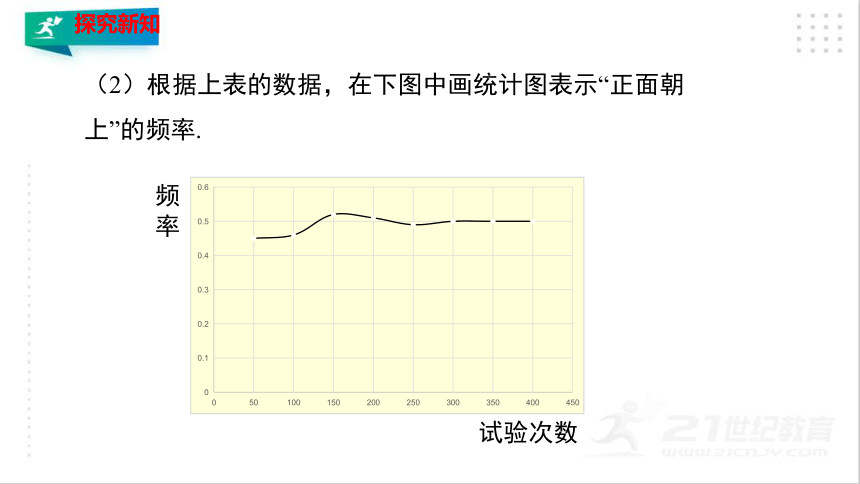
(1)抛掷一枚均匀硬币400次,每隔50次记录“正面朝上”的次数,并算出“正面朝上”的频率,完成下表:
累计抛掷次数 50 100 150 200 250 300 350 400
“正面朝上”的频数
“正面朝上”的频率
23
46
78
102
123
150
175
200
0.45
0.46
0.52
0.51
0.49
0.50
0.50
0.50
探究新知
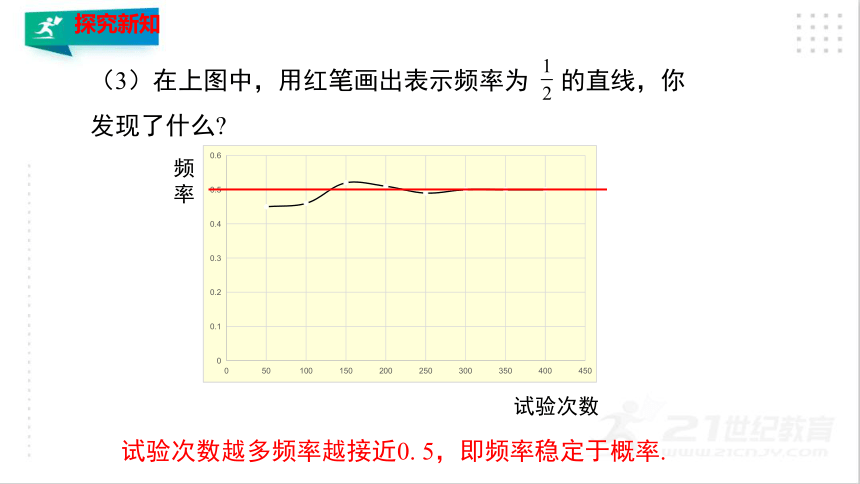
(2)根据上表的数据,在下图中画统计图表示“正面朝上”的频率.
频率
试验次数
探究新知
(3)在上图中,用红笔画出表示频率为 的直线,你发现了什么
试验次数越多频率越接近0. 5,即频率稳定于概率.
频率
试验次数
探究新知
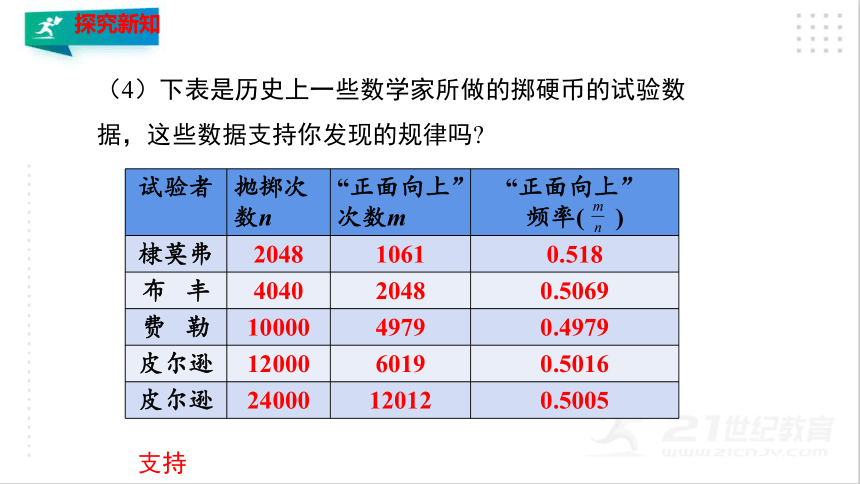
(4)下表是历史上一些数学家所做的掷硬币的试验数据,这些数据支持你发现的规律吗
试验者 抛掷次数n “正面向上”次数m “正面向上”
频率( )
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
费 勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
支持
探究新知
归纳总结
通过大量重复试验,可以用随机事件发生的频率
来估计该事件发生的概率.
思考 抛掷硬币试验的特点:
1.可能出现的结果数__________;
2.每种可能结果的可能性__________.
相等
有限
问题 如果某一随机事件,可能出现的结果是无限个,或每种可能结果发生的可能性不一致,那么我们无法用列举法求其概率,这时我们能够用频率来估计概率吗?
探究新知
从一定高度落下的图钉,着地时会有哪些可能的结果?
其中顶帽着地的可能性大吗?
做做试验来解决这个问题.
图钉落地的试验
探究新知
试验累计次数 20 40 60 80 100 120 140 160 180 200
钉帽着地的次数(频数) 9 19 36 50 61 68 77 84 95 109
钉帽着地的频率( %) 45 47.5 60 62.5 61 57 55 52.5 53 54.5
试验累计次数 220 240 260 280 300 320 340 360 380 400
钉帽着地的次数(频数) 122 135 143 155 162 177 194 203 215 224
钉帽着地的频率(%) 55 56.25 55 55 54 55 57 56.4 56.6 56
(1)选取20名同学,每位学生依次使图钉从高处落下20次,并根据试验结果填写下表.
探究新知
56.5
(%)
(2)根据上表画出统计图表示“顶帽着地”的频率.
探究新知
(3)这个试验说明了什么问题.
在图钉落地试验中,“顶帽着地”的频率随着试验次数的增加,稳定在常数56.5%附近.
探究新知
一般地,在大量重复试验中,随机事件A发生的频率 (这里n是实验总次数,它必须相当大,m是在n次试验中随机事件A发生的次数)会稳定到某个常数P.于是,我们用P这个常数表示事件A发生的概率,即
P(A)=P.
归纳总结
频率与概率的关系
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观 存在的,与每次试验无关.
稳定性
大量重复试验
探究新知
课堂练习
1.姚明在某段时间内进行定点投篮训练,其成绩如下:
试估计姚明在这段时间内定点投篮投中的概率是
_______(精确到0.1).
投篮次数 10 100 10 000
投中次数 9 89 9 012
0.9
2.在一个不透明的口袋中装有5个白球,若干个黑球,它们除颜色外其他完全相同,经过多次实验发现摸到白球的频率稳定在0.2附近,则黑球大约有________个.
20
课堂练习
3.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
课堂练习
(1)当n很大时,摸到白球的概率约为_____(精确到0.1)
(2)估算盒子里有白球________个;
0.6
24
课堂练习
4. 从生产的一批螺钉中抽取1 000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品的概率为( )
A. B. C. D.
B
课堂练习
5.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是 ( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
课堂练习
C
6.小亮是一名职业足球队员,根据以往比赛数据统计,小亮进球率为10%,他明天将参加一场比赛,下面几种说法正确的是( )
A.小亮明天的进球率为10%
B.小亮明天每射球10次必进球1次
C.小亮明天有可能进球
D.小亮明天肯定进球
课堂练习
7.小明家是养鸭专业户,有一天小亮到他家去玩,看到他家门前的水库里黑压压的一片鸭群,他先捕了100只作好标记,然后放回水库,经过一段时间,第二次捕了100只,其中带标记的鸭子有2只,小亮可估计出小明家有多少只鸭子?
【解】设小明家有鸭子x只,则有
解得:x=5000. 所以小明家大约有鸭子5000只.
课堂练习
课堂小结
频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概
率但概率与频率无关
https://www.21cnjy.com/help/help_extract.php
3.2 用频率估计概率
第三章
概率的进一步认识
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.理解试验次数较大时试验频率趋于稳定这一规律;2.结合具体情境掌握如何用频率估计概率;
3.通过概率计算进一步比较概率与频率之间的关系.
导入新课
1.复习回顾
概率:事件发生的可能性的大小
频数:在实验中,每个对象出现的次数
频率:所考察对象出现的次数与实验的总次数的比
频率=
可能发生的总结果数
用列举法求概率的条件是什么
(1)实验的所有结果是有限个
(2)各种结果的可能性相等.
A可能发生的结果数
导入新课
1
2
在纸箱里面,共放置10颗球,其中3个红球,7个黑球。摸出红球的概率是多少?
在实际摸球中,摸10次一定摸到3次红球吗?你还会发现什么?
用频率估计概率
掷硬币试验
(1)抛掷一枚均匀硬币400次,每隔50次记录“正面朝上”的次数,并算出“正面朝上”的频率,完成下表:
累计抛掷次数 50 100 150 200 250 300 350 400
“正面朝上”的频数
“正面朝上”的频率
23
46
78
102
123
150
175
200
0.45
0.46
0.52
0.51
0.49
0.50
0.50
0.50
探究新知
(2)根据上表的数据,在下图中画统计图表示“正面朝上”的频率.
频率
试验次数
探究新知
(3)在上图中,用红笔画出表示频率为 的直线,你发现了什么
试验次数越多频率越接近0. 5,即频率稳定于概率.
频率
试验次数
探究新知
(4)下表是历史上一些数学家所做的掷硬币的试验数据,这些数据支持你发现的规律吗
试验者 抛掷次数n “正面向上”次数m “正面向上”
频率( )
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
费 勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
支持
探究新知
归纳总结
通过大量重复试验,可以用随机事件发生的频率
来估计该事件发生的概率.
思考 抛掷硬币试验的特点:
1.可能出现的结果数__________;
2.每种可能结果的可能性__________.
相等
有限
问题 如果某一随机事件,可能出现的结果是无限个,或每种可能结果发生的可能性不一致,那么我们无法用列举法求其概率,这时我们能够用频率来估计概率吗?
探究新知
从一定高度落下的图钉,着地时会有哪些可能的结果?
其中顶帽着地的可能性大吗?
做做试验来解决这个问题.
图钉落地的试验
探究新知
试验累计次数 20 40 60 80 100 120 140 160 180 200
钉帽着地的次数(频数) 9 19 36 50 61 68 77 84 95 109
钉帽着地的频率( %) 45 47.5 60 62.5 61 57 55 52.5 53 54.5
试验累计次数 220 240 260 280 300 320 340 360 380 400
钉帽着地的次数(频数) 122 135 143 155 162 177 194 203 215 224
钉帽着地的频率(%) 55 56.25 55 55 54 55 57 56.4 56.6 56
(1)选取20名同学,每位学生依次使图钉从高处落下20次,并根据试验结果填写下表.
探究新知
56.5
(%)
(2)根据上表画出统计图表示“顶帽着地”的频率.
探究新知
(3)这个试验说明了什么问题.
在图钉落地试验中,“顶帽着地”的频率随着试验次数的增加,稳定在常数56.5%附近.
探究新知
一般地,在大量重复试验中,随机事件A发生的频率 (这里n是实验总次数,它必须相当大,m是在n次试验中随机事件A发生的次数)会稳定到某个常数P.于是,我们用P这个常数表示事件A发生的概率,即
P(A)=P.
归纳总结
频率与概率的关系
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观 存在的,与每次试验无关.
稳定性
大量重复试验
探究新知
课堂练习
1.姚明在某段时间内进行定点投篮训练,其成绩如下:
试估计姚明在这段时间内定点投篮投中的概率是
_______(精确到0.1).
投篮次数 10 100 10 000
投中次数 9 89 9 012
0.9
2.在一个不透明的口袋中装有5个白球,若干个黑球,它们除颜色外其他完全相同,经过多次实验发现摸到白球的频率稳定在0.2附近,则黑球大约有________个.
20
课堂练习
3.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
课堂练习
(1)当n很大时,摸到白球的概率约为_____(精确到0.1)
(2)估算盒子里有白球________个;
0.6
24
课堂练习
4. 从生产的一批螺钉中抽取1 000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品的概率为( )
A. B. C. D.
B
课堂练习
5.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是 ( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
课堂练习
C
6.小亮是一名职业足球队员,根据以往比赛数据统计,小亮进球率为10%,他明天将参加一场比赛,下面几种说法正确的是( )
A.小亮明天的进球率为10%
B.小亮明天每射球10次必进球1次
C.小亮明天有可能进球
D.小亮明天肯定进球
课堂练习
7.小明家是养鸭专业户,有一天小亮到他家去玩,看到他家门前的水库里黑压压的一片鸭群,他先捕了100只作好标记,然后放回水库,经过一段时间,第二次捕了100只,其中带标记的鸭子有2只,小亮可估计出小明家有多少只鸭子?
【解】设小明家有鸭子x只,则有
解得:x=5000. 所以小明家大约有鸭子5000只.
课堂练习
课堂小结
频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概
率但概率与频率无关
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
