第四章一次函数复习测试 2021-2022学年北师大版八年级数学上册 (Word版含答案)
文档属性
| 名称 | 第四章一次函数复习测试 2021-2022学年北师大版八年级数学上册 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 368.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 12:23:48 | ||
图片预览



文档简介
北师大版八年级数学上册第四章一次函数 复习测试
一.选择题
1. 若正比例函数y=kx的图象经过点(1,2),则k的值为( ).
A. B. -2 C. D. 2
2.下列函数:①y=πx;②y=2x-1;③y=;④y=2-1-3x;⑤y=x2-1.其中是一次函数的有( ).
A. 4个 B. 3个 C. 2个 D. 1个
3.下列的点在函数y=x-2上的是( ).
A. (0,2) B. (3,-2) C. (-3,3) D. (6,0)
4.点在函数的图象上,则代数式的值等于( ).
A.5 B.-5 C.7 D.-6
5.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式为( ).
A. y=2x+3 B. y=x-3 C. y=2x-3 D. y=-x+3
6.如图是小明从学校到家行进的路程s(m)与时间t(min)的函数图象,观察图象,从中得到如下信息,其中不正确的是( ).
A.学校离小明家1 000 m B.小明用了20 min到家
C.小明前10 min走了路程的一半 D.小明后10 min比前10 min走得快
7.若y=kx-4的函数值y随x的增大而增大,则k的值可能是下列的( ).
A. -2 B. - C. 0 D. 2
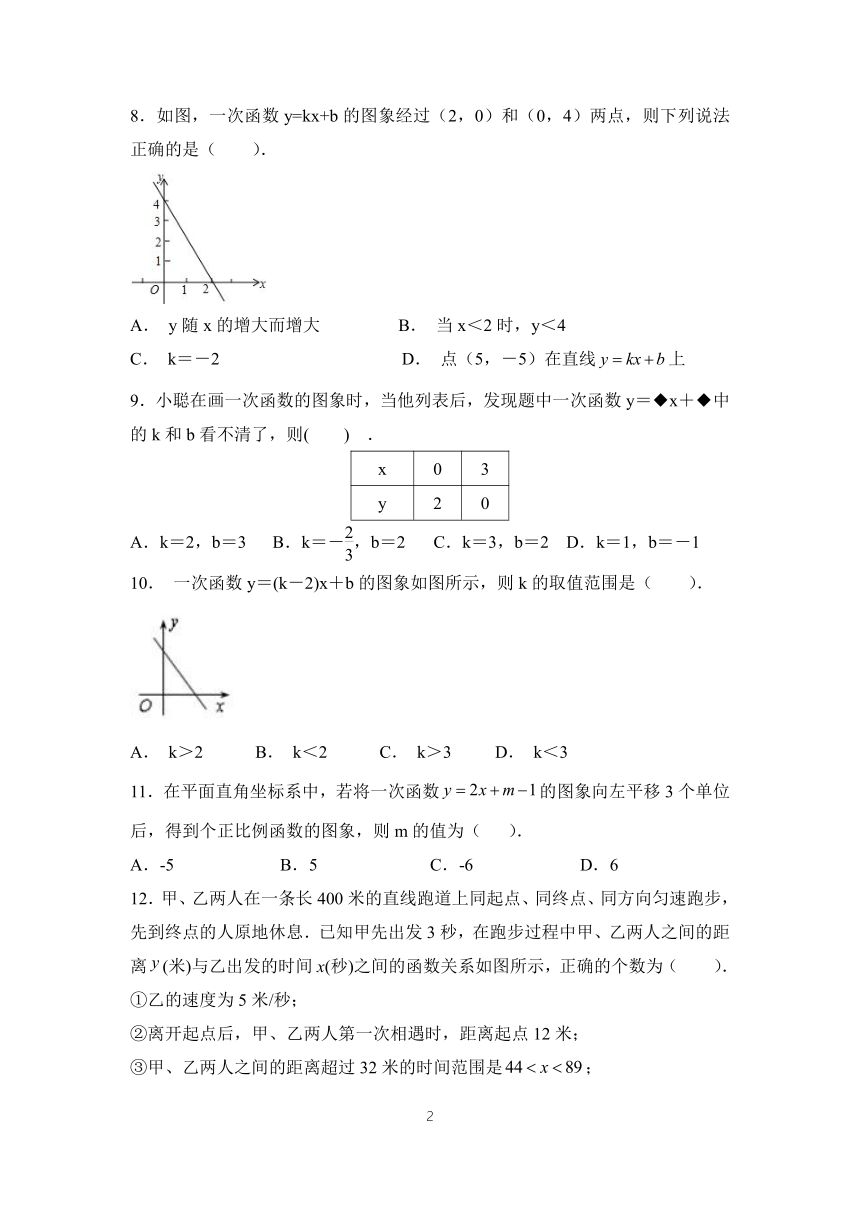
8.如图,一次函数y=kx+b的图象经过(2,0)和(0,4)两点,则下列说法正确的是( ).
A. y随x的增大而增大 B. 当x<2时,y<4
C. k=-2 D. 点(5,-5)在直线上
9.小聪在画一次函数的图象时,当他列表后,发现题中一次函数y=◆x+◆中的k和b看不清了,则( ) .
x 0 3
y 2 0
A.k=2,b=3 B.k=-,b=2 C.k=3,b=2 D.k=1,b=-1
10. 一次函数y=(k-2)x+b的图象如图所示,则k的取值范围是( ).
A. k>2 B. k<2 C. k>3 D. k<3
11.在平面直角坐标系中,若将一次函数的图象向左平移3个单位后,得到个正比例函数的图象,则m的值为( ).
A.-5 B.5 C.-6 D.6
12.甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中甲、乙两人之间的距离(米)与乙出发的时间x(秒)之间的函数关系如图所示,正确的个数为( ).
①乙的速度为5米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲、乙两人之间的距离超过32米的时间范围是;
④乙到达终点时,甲距离终点还有68米.
A.4 B.3 C.2 D.1
二.填空题
13. 已知直线y=2x+8与x轴和y轴的交点的坐标分别是 、 ;与两条坐标轴围成的三角形的面积是 .
14.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月用水不超过10 t时,水价为每吨3.0元;超过10 t时,超过的部分按每吨4.5元收费. 现有某户居民5月份用水x t(x>10),应交水费y元,则y与x的关系式为________.
15.一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为_______.
16.在正比例函数中,y的值随着x值的增大而增大,则点在第____象限.
17.如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是______
18.甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点(0,1);乙:y随x的增大而减小;丙:函数的图象不经过第三象限.根据他们的叙述,写出满足上述性质的一个函数表达式为 _____.
三.解答题
19.作出函数y=x-3的图象并回答:
(1)当x的值增加时,y的值如何变化?
(2)图象与x轴,y轴的交点坐标分别是多少?
(3)求出该图象与x轴,y轴所围成的三角形的面积.
20.在平面直角坐标系中,一次函数y=kx+b的图象经过点A(2,1),B(0,2),C(-1,n),试求n的值.
21.如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求点A,B的坐标;
(2)求当x=-2时,y的值,当y=10时,x的值;
(3)过点B作直线BP与x轴相交于点P,且使OP=2OA,求△ABP的面积.
22. 已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
(1)点A的坐标为______,点B的坐标为______;
(2)求出△AOB的面积;
(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
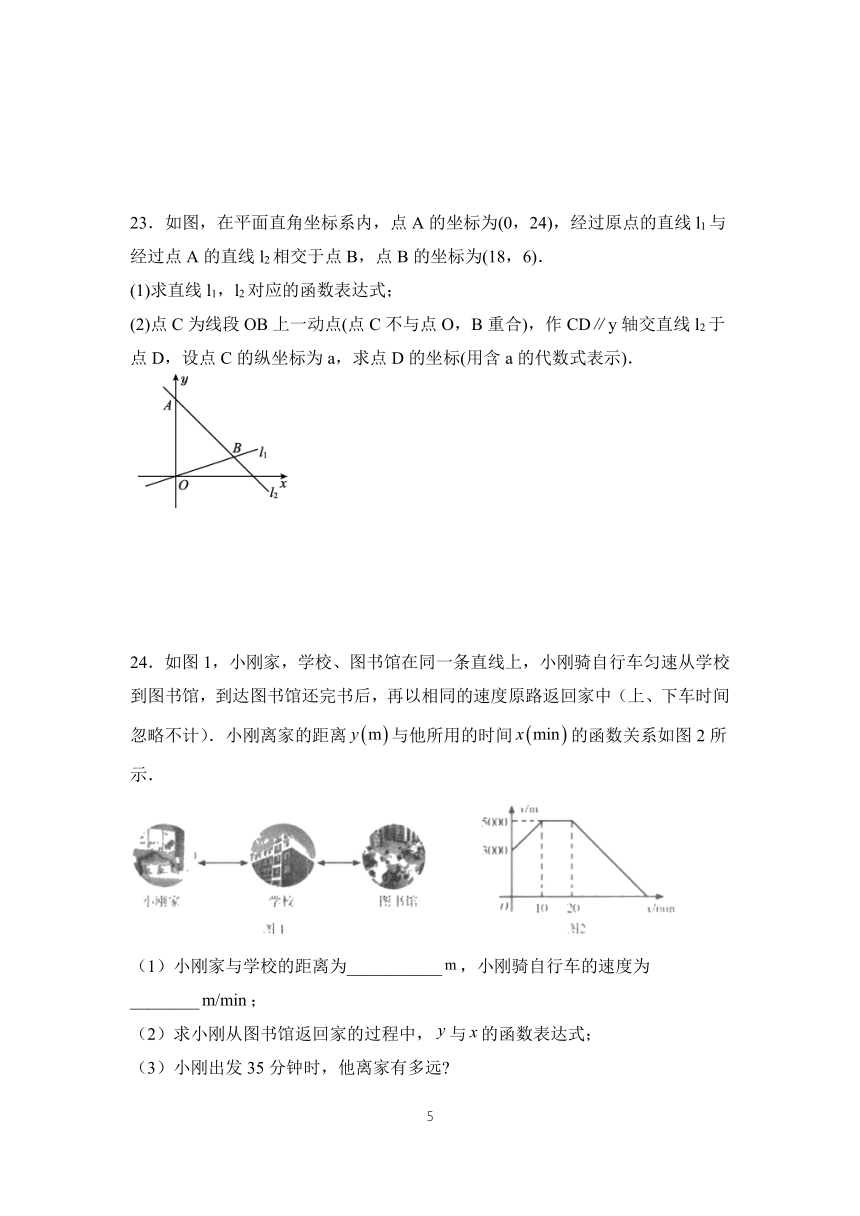
23.如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标(用含a的代数式表示).
24.如图1,小刚家,学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离与他所用的时间的函数关系如图2所示.
(1)小刚家与学校的距离为___________,小刚骑自行车的速度为________;
(2)求小刚从图书馆返回家的过程中,与的函数表达式;
(3)小刚出发35分钟时,他离家有多远
25.李师傅将容量为60升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程s(千米)与行驶时间t(小时)的关系如图所示(中途休息、加油的时间不计.当油箱中剩余油量为10升时,货车会自动显示加油提醒.设货车平均耗油量为0.1升/千米,请根据图象解答下列问题:
(1)直接写出工厂离目的地的路程;
(2)求s关于t的函数表达式;
(3)当货车显示加油提醒后,问行驶时间t在怎样的范围内货车应进站加油?
北师大版八年级数学上册第四章一次函数 复习测试答案提示
一.选择题
1. 若正比例函数y=kx的图象经过点(1,2),则k的值为( )选D.
A. B. -2 C. D. 2
2.下列函数:①y=πx;②y=2x-1;③y=;④y=2-1-3x;⑤y=x2-1.其中是一次函数的有( )选B.
A. 4个 B. 3个 C. 2个 D. 1个
3.下列的点在函数y=x-2上的是( )选D.
A. (0,2) B. (3,-2) C. (-3,3) D. (6,0)
4.(2021·内蒙古赤峰市·中考真题)点在函数的图象上,则代数式的值等于( )选B.
A.5 B.-5 C.7 D.-6
解:∵点P(a,b)在一次函数的图象上,
∴b=4a+3,
8a-2b+1=8a-2(4a+3)+1=-5,即代数式的值等于-5.
故选:B.
5.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式为( )选D.
A. y=2x+3 B. y=x-3 C. y=2x-3 D. y=-x+3
6.如图是小明从学校到家行进的路程s(m)与时间t(min)的函数图象,观察图象,从中得到如下信息,其中不正确的是( )选C.
A.学校离小明家1 000 m B.小明用了20 min到家
C.小明前10 min走了路程的一半 D.小明后10 min比前10 min走得快
7.若y=kx-4的函数值y随x的增大而增大,则k的值可能是下列的( )选D.
A. -2 B. - C. 0 D. 2
8.如图2,一次函数y=kx+b的图象经过(2,0)和(0,4)两点,则下列说法正确的是( )选C.
A. y随x的增大而增大 B. 当x<2时,y<4
C. k=-2 D. 点(5,-5)在直线上
9.小聪在画一次函数的图象时,当他列表后,发现题中一次函数y=◆x+◆中的k和b看不清了,则( ) 选B.
x 0 3
y 2 0
A.k=2,b=3 B.k=-,b=2 C.k=3,b=2 D.k=1,b=-1
10. 一次函数y=(k-2)x+b的图象如图所示,则k的取值范围是( )选B.
A. k>2 B. k<2 C. k>3 D. k<3
11.(2021·陕西中考真题)在平面直角坐标系中,若将一次函数的图象向左平移3个单位后,得到个正比例函数的图象,则m的值为( )选A.
A.-5 B.5 C.-6 D.6
12.(2021·内蒙古赤峰市·中考真题)甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中甲、乙两人之间的距离(米)与乙出发的时间x(秒)之间的函数关系如图所示,正确的个数为( )选B.
①乙的速度为5米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲、乙两人之间的距离超过32米的时间范围是;
④乙到达终点时,甲距离终点还有68米.
A.4 B.3 C.2 D.1
解:①∵乙用80秒跑完400米
∴乙的速度为=5米/秒;
故①正确;
②∵乙出发时,甲先走12米,用3秒钟,
∴甲的速度为米/秒,
∴乙追上甲所用时间为t秒,
5t-4t=12,
∴t=12秒,
∴12×5=60米,
∴离开起点后,甲、乙两人第一次相遇时,距离起点60米;
故②不正确;
③甲乙两人之间的距离超过32米设时间为t秒,
∴5(t-12)-4(t-12)32,
∴t44,
当乙到达终点停止运动后,
4 t+12400-32,
∴t89,
甲、乙两人之间的距离超过32米的时间范围是;
故③正确;
④乙到达终点时,
甲距终点距离为:400-12-4×80=400-332=68米,
甲距离终点还有68米.
故④正确;
正确的个数为3个.
故选择B.
二.填空题
13. 已知直线y=2x+8与x轴和y轴的交点的坐标分别是_(-4,0)_、_(0,8)__;与两条坐标轴围成的三角形的面积是__16___.
14.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月用水不超过10 t时,水价为每吨3.0元;超过10 t时,超过的部分按每吨4.5元收费. 现有某户居民5月份用水x t(x>10),应交水费y元,则y与x的关系式为___ y=4.5x-15_____.
15.一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为___y=-x+10____.
16.(2021·四川成都市·中考真题)在正比例函数中,y的值随着x值的增大而增大,则点在第__一__象限.
17. 如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是__y=-2x____
18.(2021·山东中考真题)甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为 ___y=-x+1____.
解:设一次函数解析式为y=kx+b,
∵函数的图象经过点(0,1),
∴b=1,
∵y随x的增大而减小,
∴k<0,取k=-1,
∴y=-x+1,此函数图象不经过第三象限,
∴满足题意的一次函数解析式为:y=-x+1(答案不唯一).
三.解答题
19.作出函数y=x-3的图象并回答:
(1)当x的值增加时,y的值如何变化?
(2)图象与x轴,y轴的交点坐标分别是多少?
(3)求出该图象与x轴,y轴所围成的三角形的面积.
解:作函数图象略.(1)y随x的增大而增大.
(2)图象与x轴的交点坐标为(6,0),与y轴的交点坐标为(0,-3).
(3)围成的三角形的面积=×6×3=9.
20.在平面直角坐标系中,一次函数y=kx+b的图象经过点A(2,1),B(0,2),C(-1,n),试求n的值.
解:.因为函数图象经过点A(2,1)和点B(0,2),
所以解得
故函数关系式为y=-x+2.
因为图象经过点(-1,n),所以n=+2=.
21.如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求点A,B的坐标;
(2)求当x=-2时,y的值,当y=10时,x的值;
(3)过点B作直线BP与x轴相交于点P,且使OP=2OA,求△ABP的面积.
解:(1)当y=0时,2x+3=0,
得x=-32,则A..
当x=0时,y=3,则B(0,3).
(2)当x=-2时,y=-1;
当y=10时,x=72.
(3)OP=2OA,A,则点P的位置有两种情况,点P在x轴的正半轴上或点P在x轴的负半轴上.
当点P在x轴负半轴上时,P(-3,0),
则△ABP的面积为××3=;
当点P在x轴的正半轴上时,P(3,0),
则△ABP的面积为×3×=.
22. 已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
(1)点A的坐标为______,点B的坐标为______;
(2)求出△AOB的面积;
(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
解:(1)当y=0时,-2x+6=0,解得x=3,则A点的坐标为(3,0);当x=0时,y =-2x+6=6,则B点的坐标为(0,6).
(2)S△AOB=×3×6=9.
(3)存在.理由如下:设点C的坐标为(t,-2t+6).
因为△AOC的面积等于△AOB的面积,所以×3×|-2t+6|=9,解得t1=6,t2=0(与点B重合,舍去).所以点C的坐标为(6,-6).
23.如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标(用含a的代数式表示).
解:(1)设直线l1对应的函数表达式为y=k1x,由它过点(18,6)得18k1=6,解得k1=, 所以直线l1对应的函数表达式为y=x;
设直线l2对应的函数表达式为y=k2x+b,由它过点A(0,24),B(18,6)得b=24,18k2+b=6,解得k2=-1,所以直线l2对应的函数表达式为y=-x+24.
(2)因为点C在直线l1上,且点C的纵坐标为a,所以a=x.
所以x=3a,故点C的坐标为(3a,a).
因为CD∥y轴,
所以点D的横坐标为3a.
因为点D在直线l2上,
所以点D的纵坐标为-3a+24.
所以点D的坐标为(3a,-3a+24).
24.(2021·甘肃武威市·中考真题)如图1,小刚家,学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离与他所用的时间的函数关系如图2所示.
(1)小刚家与学校的距离为___________,小刚骑自行车的速度为________;
(2)求小刚从图书馆返回家的过程中,与的函数表达式;
(3)小刚出发35分钟时,他离家有多远
解:(1)小刚骑自行车匀速从学校到图书馆,从起点3000m处为学校出发去5000m处为图书馆,
∴小刚家与学校的距离为3000m,
小刚骑自行车匀速行驶10分钟,从3000m走到5000m,
行驶的路程为5000-3000=2000m,
骑自行车的速度为2000÷10=200m/min,
故答案为:3000,200;
(2)小刚从图书馆返回家的时间:.
总时间:.
设返回时与的函数表达式为,
把代入得:,
解得,,
.
(3)小刚出发35分钟,即当时,
,
答:此时他离家.
25.(2021·浙江丽水市·中考真题)李师傅将容量为60升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程s(千米)与行驶时间t(小时)的关系如图所示(中途休息、加油的时间不计.当油箱中剩余油量为10升时,货车会自动显示加油提醒.设货车平均耗油量为0.1升/千米,请根据图象解答下列问题:
(1)直接写出工厂离目的地的路程;
(2)求s关于t的函数表达式;
(3)当货车显示加油提醒后,问行驶时间t在怎样的范围内货车应进站加油?
解:(1)由图象,得时,,
答:工厂离目的地的路程为880千米.
(2)设,将和分别代入表达式,
得,解得,
∴s关于t的函数表达式为.
(3)当油箱中剩余油量为10升时,(千米),
,解得(小时).
当油箱中剩余油量为0升时,(千米),
,解得(小时).
随t的增大而减小,
的取值范围是.
一.选择题
1. 若正比例函数y=kx的图象经过点(1,2),则k的值为( ).
A. B. -2 C. D. 2
2.下列函数:①y=πx;②y=2x-1;③y=;④y=2-1-3x;⑤y=x2-1.其中是一次函数的有( ).
A. 4个 B. 3个 C. 2个 D. 1个
3.下列的点在函数y=x-2上的是( ).
A. (0,2) B. (3,-2) C. (-3,3) D. (6,0)
4.点在函数的图象上,则代数式的值等于( ).
A.5 B.-5 C.7 D.-6
5.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式为( ).
A. y=2x+3 B. y=x-3 C. y=2x-3 D. y=-x+3
6.如图是小明从学校到家行进的路程s(m)与时间t(min)的函数图象,观察图象,从中得到如下信息,其中不正确的是( ).
A.学校离小明家1 000 m B.小明用了20 min到家
C.小明前10 min走了路程的一半 D.小明后10 min比前10 min走得快
7.若y=kx-4的函数值y随x的增大而增大,则k的值可能是下列的( ).
A. -2 B. - C. 0 D. 2
8.如图,一次函数y=kx+b的图象经过(2,0)和(0,4)两点,则下列说法正确的是( ).
A. y随x的增大而增大 B. 当x<2时,y<4
C. k=-2 D. 点(5,-5)在直线上
9.小聪在画一次函数的图象时,当他列表后,发现题中一次函数y=◆x+◆中的k和b看不清了,则( ) .
x 0 3
y 2 0
A.k=2,b=3 B.k=-,b=2 C.k=3,b=2 D.k=1,b=-1
10. 一次函数y=(k-2)x+b的图象如图所示,则k的取值范围是( ).
A. k>2 B. k<2 C. k>3 D. k<3
11.在平面直角坐标系中,若将一次函数的图象向左平移3个单位后,得到个正比例函数的图象,则m的值为( ).
A.-5 B.5 C.-6 D.6
12.甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中甲、乙两人之间的距离(米)与乙出发的时间x(秒)之间的函数关系如图所示,正确的个数为( ).
①乙的速度为5米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲、乙两人之间的距离超过32米的时间范围是;
④乙到达终点时,甲距离终点还有68米.
A.4 B.3 C.2 D.1
二.填空题
13. 已知直线y=2x+8与x轴和y轴的交点的坐标分别是 、 ;与两条坐标轴围成的三角形的面积是 .
14.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月用水不超过10 t时,水价为每吨3.0元;超过10 t时,超过的部分按每吨4.5元收费. 现有某户居民5月份用水x t(x>10),应交水费y元,则y与x的关系式为________.
15.一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为_______.
16.在正比例函数中,y的值随着x值的增大而增大,则点在第____象限.
17.如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是______
18.甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点(0,1);乙:y随x的增大而减小;丙:函数的图象不经过第三象限.根据他们的叙述,写出满足上述性质的一个函数表达式为 _____.
三.解答题
19.作出函数y=x-3的图象并回答:
(1)当x的值增加时,y的值如何变化?
(2)图象与x轴,y轴的交点坐标分别是多少?
(3)求出该图象与x轴,y轴所围成的三角形的面积.
20.在平面直角坐标系中,一次函数y=kx+b的图象经过点A(2,1),B(0,2),C(-1,n),试求n的值.
21.如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求点A,B的坐标;
(2)求当x=-2时,y的值,当y=10时,x的值;
(3)过点B作直线BP与x轴相交于点P,且使OP=2OA,求△ABP的面积.
22. 已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
(1)点A的坐标为______,点B的坐标为______;
(2)求出△AOB的面积;
(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
23.如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标(用含a的代数式表示).
24.如图1,小刚家,学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离与他所用的时间的函数关系如图2所示.
(1)小刚家与学校的距离为___________,小刚骑自行车的速度为________;
(2)求小刚从图书馆返回家的过程中,与的函数表达式;
(3)小刚出发35分钟时,他离家有多远
25.李师傅将容量为60升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程s(千米)与行驶时间t(小时)的关系如图所示(中途休息、加油的时间不计.当油箱中剩余油量为10升时,货车会自动显示加油提醒.设货车平均耗油量为0.1升/千米,请根据图象解答下列问题:
(1)直接写出工厂离目的地的路程;
(2)求s关于t的函数表达式;
(3)当货车显示加油提醒后,问行驶时间t在怎样的范围内货车应进站加油?
北师大版八年级数学上册第四章一次函数 复习测试答案提示
一.选择题
1. 若正比例函数y=kx的图象经过点(1,2),则k的值为( )选D.
A. B. -2 C. D. 2
2.下列函数:①y=πx;②y=2x-1;③y=;④y=2-1-3x;⑤y=x2-1.其中是一次函数的有( )选B.
A. 4个 B. 3个 C. 2个 D. 1个
3.下列的点在函数y=x-2上的是( )选D.
A. (0,2) B. (3,-2) C. (-3,3) D. (6,0)
4.(2021·内蒙古赤峰市·中考真题)点在函数的图象上,则代数式的值等于( )选B.
A.5 B.-5 C.7 D.-6
解:∵点P(a,b)在一次函数的图象上,
∴b=4a+3,
8a-2b+1=8a-2(4a+3)+1=-5,即代数式的值等于-5.
故选:B.
5.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式为( )选D.
A. y=2x+3 B. y=x-3 C. y=2x-3 D. y=-x+3
6.如图是小明从学校到家行进的路程s(m)与时间t(min)的函数图象,观察图象,从中得到如下信息,其中不正确的是( )选C.
A.学校离小明家1 000 m B.小明用了20 min到家
C.小明前10 min走了路程的一半 D.小明后10 min比前10 min走得快
7.若y=kx-4的函数值y随x的增大而增大,则k的值可能是下列的( )选D.
A. -2 B. - C. 0 D. 2
8.如图2,一次函数y=kx+b的图象经过(2,0)和(0,4)两点,则下列说法正确的是( )选C.
A. y随x的增大而增大 B. 当x<2时,y<4
C. k=-2 D. 点(5,-5)在直线上
9.小聪在画一次函数的图象时,当他列表后,发现题中一次函数y=◆x+◆中的k和b看不清了,则( ) 选B.
x 0 3
y 2 0
A.k=2,b=3 B.k=-,b=2 C.k=3,b=2 D.k=1,b=-1
10. 一次函数y=(k-2)x+b的图象如图所示,则k的取值范围是( )选B.
A. k>2 B. k<2 C. k>3 D. k<3
11.(2021·陕西中考真题)在平面直角坐标系中,若将一次函数的图象向左平移3个单位后,得到个正比例函数的图象,则m的值为( )选A.
A.-5 B.5 C.-6 D.6
12.(2021·内蒙古赤峰市·中考真题)甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中甲、乙两人之间的距离(米)与乙出发的时间x(秒)之间的函数关系如图所示,正确的个数为( )选B.
①乙的速度为5米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲、乙两人之间的距离超过32米的时间范围是;
④乙到达终点时,甲距离终点还有68米.
A.4 B.3 C.2 D.1
解:①∵乙用80秒跑完400米
∴乙的速度为=5米/秒;
故①正确;
②∵乙出发时,甲先走12米,用3秒钟,
∴甲的速度为米/秒,
∴乙追上甲所用时间为t秒,
5t-4t=12,
∴t=12秒,
∴12×5=60米,
∴离开起点后,甲、乙两人第一次相遇时,距离起点60米;
故②不正确;
③甲乙两人之间的距离超过32米设时间为t秒,
∴5(t-12)-4(t-12)32,
∴t44,
当乙到达终点停止运动后,
4 t+12400-32,
∴t89,
甲、乙两人之间的距离超过32米的时间范围是;
故③正确;
④乙到达终点时,
甲距终点距离为:400-12-4×80=400-332=68米,
甲距离终点还有68米.
故④正确;
正确的个数为3个.
故选择B.
二.填空题
13. 已知直线y=2x+8与x轴和y轴的交点的坐标分别是_(-4,0)_、_(0,8)__;与两条坐标轴围成的三角形的面积是__16___.
14.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月用水不超过10 t时,水价为每吨3.0元;超过10 t时,超过的部分按每吨4.5元收费. 现有某户居民5月份用水x t(x>10),应交水费y元,则y与x的关系式为___ y=4.5x-15_____.
15.一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为___y=-x+10____.
16.(2021·四川成都市·中考真题)在正比例函数中,y的值随着x值的增大而增大,则点在第__一__象限.
17. 如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是__y=-2x____
18.(2021·山东中考真题)甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为 ___y=-x+1____.
解:设一次函数解析式为y=kx+b,
∵函数的图象经过点(0,1),
∴b=1,
∵y随x的增大而减小,
∴k<0,取k=-1,
∴y=-x+1,此函数图象不经过第三象限,
∴满足题意的一次函数解析式为:y=-x+1(答案不唯一).
三.解答题
19.作出函数y=x-3的图象并回答:
(1)当x的值增加时,y的值如何变化?
(2)图象与x轴,y轴的交点坐标分别是多少?
(3)求出该图象与x轴,y轴所围成的三角形的面积.
解:作函数图象略.(1)y随x的增大而增大.
(2)图象与x轴的交点坐标为(6,0),与y轴的交点坐标为(0,-3).
(3)围成的三角形的面积=×6×3=9.
20.在平面直角坐标系中,一次函数y=kx+b的图象经过点A(2,1),B(0,2),C(-1,n),试求n的值.
解:.因为函数图象经过点A(2,1)和点B(0,2),
所以解得
故函数关系式为y=-x+2.
因为图象经过点(-1,n),所以n=+2=.
21.如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求点A,B的坐标;
(2)求当x=-2时,y的值,当y=10时,x的值;
(3)过点B作直线BP与x轴相交于点P,且使OP=2OA,求△ABP的面积.
解:(1)当y=0时,2x+3=0,
得x=-32,则A..
当x=0时,y=3,则B(0,3).
(2)当x=-2时,y=-1;
当y=10时,x=72.
(3)OP=2OA,A,则点P的位置有两种情况,点P在x轴的正半轴上或点P在x轴的负半轴上.
当点P在x轴负半轴上时,P(-3,0),
则△ABP的面积为××3=;
当点P在x轴的正半轴上时,P(3,0),
则△ABP的面积为×3×=.
22. 已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
(1)点A的坐标为______,点B的坐标为______;
(2)求出△AOB的面积;
(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
解:(1)当y=0时,-2x+6=0,解得x=3,则A点的坐标为(3,0);当x=0时,y =-2x+6=6,则B点的坐标为(0,6).
(2)S△AOB=×3×6=9.
(3)存在.理由如下:设点C的坐标为(t,-2t+6).
因为△AOC的面积等于△AOB的面积,所以×3×|-2t+6|=9,解得t1=6,t2=0(与点B重合,舍去).所以点C的坐标为(6,-6).
23.如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标(用含a的代数式表示).
解:(1)设直线l1对应的函数表达式为y=k1x,由它过点(18,6)得18k1=6,解得k1=, 所以直线l1对应的函数表达式为y=x;
设直线l2对应的函数表达式为y=k2x+b,由它过点A(0,24),B(18,6)得b=24,18k2+b=6,解得k2=-1,所以直线l2对应的函数表达式为y=-x+24.
(2)因为点C在直线l1上,且点C的纵坐标为a,所以a=x.
所以x=3a,故点C的坐标为(3a,a).
因为CD∥y轴,
所以点D的横坐标为3a.
因为点D在直线l2上,
所以点D的纵坐标为-3a+24.
所以点D的坐标为(3a,-3a+24).
24.(2021·甘肃武威市·中考真题)如图1,小刚家,学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离与他所用的时间的函数关系如图2所示.
(1)小刚家与学校的距离为___________,小刚骑自行车的速度为________;
(2)求小刚从图书馆返回家的过程中,与的函数表达式;
(3)小刚出发35分钟时,他离家有多远
解:(1)小刚骑自行车匀速从学校到图书馆,从起点3000m处为学校出发去5000m处为图书馆,
∴小刚家与学校的距离为3000m,
小刚骑自行车匀速行驶10分钟,从3000m走到5000m,
行驶的路程为5000-3000=2000m,
骑自行车的速度为2000÷10=200m/min,
故答案为:3000,200;
(2)小刚从图书馆返回家的时间:.
总时间:.
设返回时与的函数表达式为,
把代入得:,
解得,,
.
(3)小刚出发35分钟,即当时,
,
答:此时他离家.
25.(2021·浙江丽水市·中考真题)李师傅将容量为60升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程s(千米)与行驶时间t(小时)的关系如图所示(中途休息、加油的时间不计.当油箱中剩余油量为10升时,货车会自动显示加油提醒.设货车平均耗油量为0.1升/千米,请根据图象解答下列问题:
(1)直接写出工厂离目的地的路程;
(2)求s关于t的函数表达式;
(3)当货车显示加油提醒后,问行驶时间t在怎样的范围内货车应进站加油?
解:(1)由图象,得时,,
答:工厂离目的地的路程为880千米.
(2)设,将和分别代入表达式,
得,解得,
∴s关于t的函数表达式为.
(3)当油箱中剩余油量为10升时,(千米),
,解得(小时).
当油箱中剩余油量为0升时,(千米),
,解得(小时).
随t的增大而减小,
的取值范围是.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
