3.1.1椭圆的标准方程(共18张PPT)
文档属性
| 名称 | 3.1.1椭圆的标准方程(共18张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
天宫3号飞船运行轨迹
课题引入
第三章 圆锥曲线的方程
3.1.1 椭圆及其标准方程
1 什么是圆?
2 取一条定长的细绳,把它的两端固定在平面内的同一点上,用铅笔尖把绳子拉紧,使笔尖在平面内慢慢移动,问笔尖画出的图形是什么?
3 若将细绳两端分开,并且固定在平面内的F1,F2两点.用铅笔尖把绳子拉紧,使笔尖在平面内慢慢移动,问笔尖画出的图形又是什么呢?
平面内到定点的距离等于定长的点的轨迹是圆.
平面内到定点的距离等于定长的点的轨迹是圆.
新知讲解
在平面内动点M到两个定点 的距离之和等于定值的点的轨迹是否一定为椭圆?
想一想
椭圆的定义
我们把平面内与两个定点F1,F2的距离的和等于常数(大于 |F1F2| )的点的轨迹叫做椭圆.
这两个定点F1、F2叫做椭圆的焦点.两个焦点的距离叫做焦距.焦距的一半称为半焦距.
注意:椭圆定义中容易遗漏的地方:
(1)两个定点间的距离(焦距)--- | F1F2 |=2c
(2)与两个定点F1,F2的距离的和等于常数---| MF1 |+|M F2 |=2a
(3)2a>2c
2c
M
F1
F2
新知讲解
问题:求方程的一般步骤是什么?
①建系、 ② 设点 ③列式 ④化简 ⑤证明
想一想:(1)圆的方程是怎么求出来的?
(2)椭圆方程怎么求?
研讨探究
推导方程
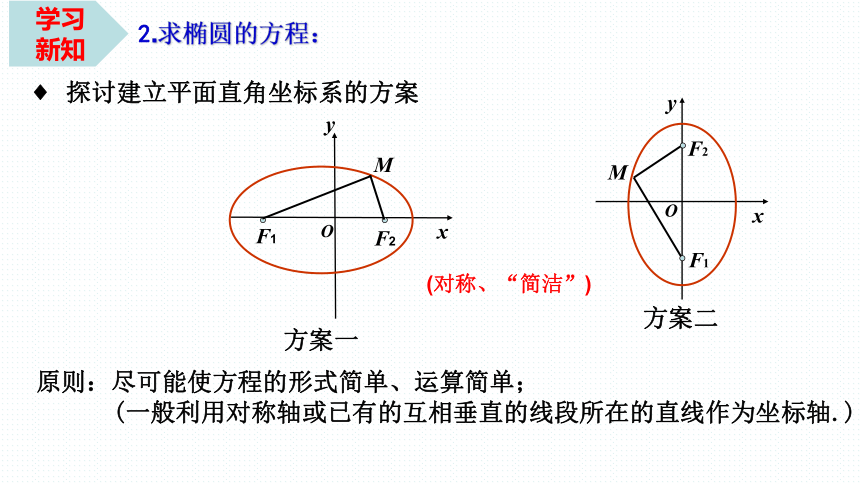
探讨建立平面直角坐标系的方案
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
2.求椭圆的方程:
原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)
(对称、“简洁”)
学习
新知
取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),M与F1和F2的距离的和等于2a (2a>2c) ,则F1、F2的坐标分别是(-c,0),(c,0) .
x
F1
F2
M
0
y
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
代入坐标
椭圆方程推导
椭圆方程推导
椭圆方程推导
叫做椭圆的标准方程。
它表示焦点在x轴上,两个焦点分别是 的椭圆方程 ,
这里c2=a2-b2。
如果椭圆的焦点在y轴上,那么椭圆的标准方程又是怎样的呢
也是椭圆的标准方程。
椭圆标准方程
学习
新知
它表示焦点在y轴上,两个焦点分别是 F1(0,-c),F2(0,c) 的椭圆方程 ,这里c2=a2-b2。
图 形
方 程
焦 点
F1(-c,0),F2(c,0)
a,b,c之间
的关系
c2=a2-b2
| MF1 | + | MF2 | =2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
两类标准方程的对照表
F1(0,-c),F2(0,c)
焦点在分母大的那个轴上.
椭圆的标准方程
表示的一定是焦点
在坐标轴上,中心在坐标原点的椭圆;
方程的左边是平方和,
右边是1.
练习1.下列方程哪些表示椭圆?
若是,则判定其焦点在何轴?
并指明 ,写出焦点坐标.
巩固练习
例题
讲评
你还能用其他方法求它的标准方程吗?试比较不同方法的特点.
4
例题
讲评
方法二:方程思维(待定系数法)
课本p109 练习1,2
例3、如图,在圆x2+y2=4上任取一点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
相关点分析法:即利用中间变量求曲线方程.
o
x
y
P
M
D
例题讲评
分析:点P在圆x2+y2=4上运动,点P的运动引起点M运动,我们可以由M为线段PD的中点得到点M与点P坐标之间的关系式,并由点P的坐标满足圆的方程得到点M的坐标所满足的方程.
因为点P(x0,y0)在圆x2+y2=4上,所以x02+y02=4 ①
把x0=x, y0=2y代入方程①,得x2+4y2=4, 即
所以点M的轨迹是椭圆.
例题讲评
解:设点M的坐标为(x,y),因为点A的坐标是(-5,0),点B的坐标是(5,0),
点M的轨迹是除去(-5,0),(5,0)两点的椭圆.
课本第109页练习第4题
小结
(1)椭圆的定义
(2)椭圆的标准方程
焦点在x轴:
焦点在y轴:
(3)求椭圆的标准方程的方法
代定系数法
定义法
天宫3号飞船运行轨迹
课题引入
第三章 圆锥曲线的方程
3.1.1 椭圆及其标准方程
1 什么是圆?
2 取一条定长的细绳,把它的两端固定在平面内的同一点上,用铅笔尖把绳子拉紧,使笔尖在平面内慢慢移动,问笔尖画出的图形是什么?
3 若将细绳两端分开,并且固定在平面内的F1,F2两点.用铅笔尖把绳子拉紧,使笔尖在平面内慢慢移动,问笔尖画出的图形又是什么呢?
平面内到定点的距离等于定长的点的轨迹是圆.
平面内到定点的距离等于定长的点的轨迹是圆.
新知讲解
在平面内动点M到两个定点 的距离之和等于定值的点的轨迹是否一定为椭圆?
想一想
椭圆的定义
我们把平面内与两个定点F1,F2的距离的和等于常数(大于 |F1F2| )的点的轨迹叫做椭圆.
这两个定点F1、F2叫做椭圆的焦点.两个焦点的距离叫做焦距.焦距的一半称为半焦距.
注意:椭圆定义中容易遗漏的地方:
(1)两个定点间的距离(焦距)--- | F1F2 |=2c
(2)与两个定点F1,F2的距离的和等于常数---| MF1 |+|M F2 |=2a
(3)2a>2c
2c
M
F1
F2
新知讲解
问题:求方程的一般步骤是什么?
①建系、 ② 设点 ③列式 ④化简 ⑤证明
想一想:(1)圆的方程是怎么求出来的?
(2)椭圆方程怎么求?
研讨探究
推导方程
探讨建立平面直角坐标系的方案
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
2.求椭圆的方程:
原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)
(对称、“简洁”)
学习
新知
取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),M与F1和F2的距离的和等于2a (2a>2c) ,则F1、F2的坐标分别是(-c,0),(c,0) .
x
F1
F2
M
0
y
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
代入坐标
椭圆方程推导
椭圆方程推导
椭圆方程推导
叫做椭圆的标准方程。
它表示焦点在x轴上,两个焦点分别是 的椭圆方程 ,
这里c2=a2-b2。
如果椭圆的焦点在y轴上,那么椭圆的标准方程又是怎样的呢
也是椭圆的标准方程。
椭圆标准方程
学习
新知
它表示焦点在y轴上,两个焦点分别是 F1(0,-c),F2(0,c) 的椭圆方程 ,这里c2=a2-b2。
图 形
方 程
焦 点
F1(-c,0),F2(c,0)
a,b,c之间
的关系
c2=a2-b2
| MF1 | + | MF2 | =2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
两类标准方程的对照表
F1(0,-c),F2(0,c)
焦点在分母大的那个轴上.
椭圆的标准方程
表示的一定是焦点
在坐标轴上,中心在坐标原点的椭圆;
方程的左边是平方和,
右边是1.
练习1.下列方程哪些表示椭圆?
若是,则判定其焦点在何轴?
并指明 ,写出焦点坐标.
巩固练习
例题
讲评
你还能用其他方法求它的标准方程吗?试比较不同方法的特点.
4
例题
讲评
方法二:方程思维(待定系数法)
课本p109 练习1,2
例3、如图,在圆x2+y2=4上任取一点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
相关点分析法:即利用中间变量求曲线方程.
o
x
y
P
M
D
例题讲评
分析:点P在圆x2+y2=4上运动,点P的运动引起点M运动,我们可以由M为线段PD的中点得到点M与点P坐标之间的关系式,并由点P的坐标满足圆的方程得到点M的坐标所满足的方程.
因为点P(x0,y0)在圆x2+y2=4上,所以x02+y02=4 ①
把x0=x, y0=2y代入方程①,得x2+4y2=4, 即
所以点M的轨迹是椭圆.
例题讲评
解:设点M的坐标为(x,y),因为点A的坐标是(-5,0),点B的坐标是(5,0),
点M的轨迹是除去(-5,0),(5,0)两点的椭圆.
课本第109页练习第4题
小结
(1)椭圆的定义
(2)椭圆的标准方程
焦点在x轴:
焦点在y轴:
(3)求椭圆的标准方程的方法
代定系数法
定义法
