2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.2.1双曲线及其标准方程 课件(共30张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.2.1双曲线及其标准方程 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 20:00:57 | ||
图片预览











文档简介
(共30张PPT)
我们知道,与两个定点距离的和为非零常数(大于两个定点间的距离)的点的轨迹是椭圆,那么,与两个定点距离的差为非零常数的点的轨迹是什么?
[ 思考 ]
如图,取一条拉链,拉
开它的一部分,在拉开的两 边上各选择一点,分别固定
在点F1, F2上, 把笔尖放在点
M处, 随着拉链逐渐拉开或者
闭拢, 笔尖所经过的点就画出一条曲线, 这条曲线是满足下面条件的点的集合: P ={ M | |MF1| - |MF2| = 常数 }
如果使点M到点F2的距
离减去到点F1的距离所得的
差等于同一个常数,就得到 另一条曲线,这条曲线是满
足下面条件的点的集合: P ={ M | |MF2| - |MF1| = 常数 }
如果使点M到点F2的距
离减去到点F1的距离所得的
差等于同一个常数,就得到 另一条曲线,这条曲线是满
足下面条件的点的集合: P ={ M | |MF2| - |MF1| = 常数 }
这两条曲线合起来叫做双曲线,每一条叫做双曲线的一支.
1、双曲线的定义:
我们把平面内与两个定点F1、F2的距离的差的绝对值等于常数(小于| F1F2 |) 的点的轨迹叫做双曲线, 这两个定点叫做双曲线的焦点, 两焦点间的距离叫做双曲线的焦距.
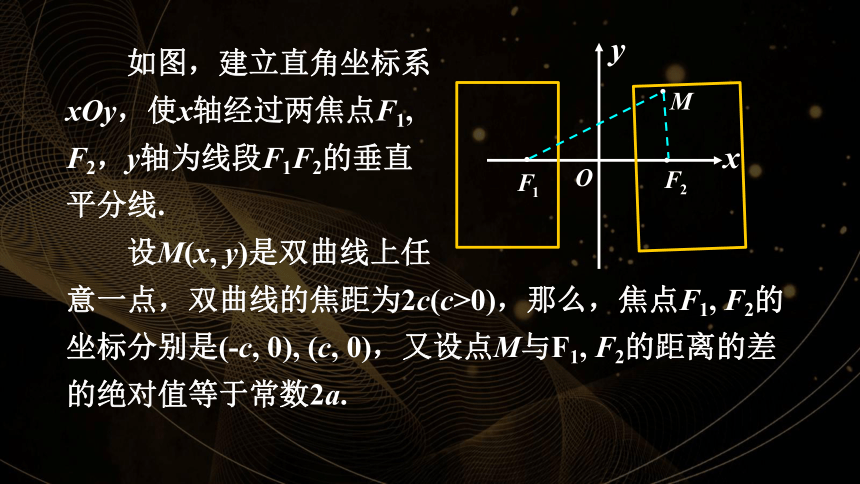
如图,建立直角坐标系
xOy,使x轴经过两焦点F1,
F2,y轴为线段F1F2的垂直
平分线. 设M(x, y)是双曲线上任
意一点,双曲线的焦距为2c(c>0),那么,焦点F1, F2的坐标分别是(-c, 0), (c, 0),又设点M与F1, F2的距离的差的绝对值等于常数2a.
由定义可知,双曲线就是集合 P ={ M | | |MF1| - |MF2| | = 2a }
这样, 我们把方程(2)叫做双曲线的标准方程. 它表示焦点在x轴上, 焦点分别是F1(-c, 0), F2 (c, 0)的双曲线,这里c2=a2+b2 .
类比焦点在y轴上的椭圆标准
方程, 如图, 双曲线的焦点分别是
F1(0, -c), F2 (0, c), a, b的意义同上,
这时双曲线的标准方程是什么?
[ 思考 ]
类比焦点在y轴上的椭圆标准
方程, 如图, 双曲线的焦点分别是
F1(0, -c), F2 (0, c), a, b的意义同上,
这时双曲线的标准方程是什么?
[ 思考 ]
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
|MF1|+|MF2|=2a
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
F (±c, 0)
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
F (±c, 0)
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
F (0, ±c)
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
F (±c, 0)
a>b>0,a2=b2+c2
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
F (0, ±c)
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
F (±c, 0)
a>0, b>0, 但a不一定大于b, c2=a2+b2
a>b>0,a2=b2+c2
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
F (0, ±c)
已知双曲线两个焦点分别为F1(-5, 0), F2(5,0), 双曲线上一点P到F1, F2距离差的绝对值等于6,求双曲线的标准方程.
【例1】
已知AB两地相距800m,在A地听到炮弹爆炸声比B地晚2s, 且声速为340m/s, 求炮弹爆炸点的轨迹方程.
【例2】
[ 探究 ]
【拓展练习】
【练习1】
【练习2】
与圆(x+3)2+y2=1及圆(x-3)2+y2=9都外切的圆的圆心在( )
A. 一个椭圆上
B. 双曲线的一支上
C. 一条抛物线上
D. 一个圆上
【练习3】
1. 双曲线的标准方程的外在形式与其焦点所在坐标轴有关,由双曲线方程分析有关性质,一般先将其方程化为标准方程,再确定a、b、c的值.
2. 求双曲线标准方程时,若不知焦点所在坐标轴, 可设双曲线方程为Ax2+By2=1,用代定系数法求解.
《考一本》第14课时
【练习4】
【练习5】
我们知道,与两个定点距离的和为非零常数(大于两个定点间的距离)的点的轨迹是椭圆,那么,与两个定点距离的差为非零常数的点的轨迹是什么?
[ 思考 ]
如图,取一条拉链,拉
开它的一部分,在拉开的两 边上各选择一点,分别固定
在点F1, F2上, 把笔尖放在点
M处, 随着拉链逐渐拉开或者
闭拢, 笔尖所经过的点就画出一条曲线, 这条曲线是满足下面条件的点的集合: P ={ M | |MF1| - |MF2| = 常数 }
如果使点M到点F2的距
离减去到点F1的距离所得的
差等于同一个常数,就得到 另一条曲线,这条曲线是满
足下面条件的点的集合: P ={ M | |MF2| - |MF1| = 常数 }
如果使点M到点F2的距
离减去到点F1的距离所得的
差等于同一个常数,就得到 另一条曲线,这条曲线是满
足下面条件的点的集合: P ={ M | |MF2| - |MF1| = 常数 }
这两条曲线合起来叫做双曲线,每一条叫做双曲线的一支.
1、双曲线的定义:
我们把平面内与两个定点F1、F2的距离的差的绝对值等于常数(小于| F1F2 |) 的点的轨迹叫做双曲线, 这两个定点叫做双曲线的焦点, 两焦点间的距离叫做双曲线的焦距.
如图,建立直角坐标系
xOy,使x轴经过两焦点F1,
F2,y轴为线段F1F2的垂直
平分线. 设M(x, y)是双曲线上任
意一点,双曲线的焦距为2c(c>0),那么,焦点F1, F2的坐标分别是(-c, 0), (c, 0),又设点M与F1, F2的距离的差的绝对值等于常数2a.
由定义可知,双曲线就是集合 P ={ M | | |MF1| - |MF2| | = 2a }
这样, 我们把方程(2)叫做双曲线的标准方程. 它表示焦点在x轴上, 焦点分别是F1(-c, 0), F2 (c, 0)的双曲线,这里c2=a2+b2 .
类比焦点在y轴上的椭圆标准
方程, 如图, 双曲线的焦点分别是
F1(0, -c), F2 (0, c), a, b的意义同上,
这时双曲线的标准方程是什么?
[ 思考 ]
类比焦点在y轴上的椭圆标准
方程, 如图, 双曲线的焦点分别是
F1(0, -c), F2 (0, c), a, b的意义同上,
这时双曲线的标准方程是什么?
[ 思考 ]
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
|MF1|+|MF2|=2a
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
F (±c, 0)
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
F (±c, 0)
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
F (0, ±c)
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
F (±c, 0)
a>b>0,a2=b2+c2
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
F (0, ±c)
3、双曲线方程与椭圆方程之间的区别
椭圆 双曲线
定义
方程
焦点
a. b. c
的关系
F (±c, 0)
F (±c, 0)
a>0, b>0, 但a不一定大于b, c2=a2+b2
a>b>0,a2=b2+c2
| |MF1|-|MF2| |=2a
|MF1|+|MF2|=2a
F (0, ±c)
F (0, ±c)
已知双曲线两个焦点分别为F1(-5, 0), F2(5,0), 双曲线上一点P到F1, F2距离差的绝对值等于6,求双曲线的标准方程.
【例1】
已知AB两地相距800m,在A地听到炮弹爆炸声比B地晚2s, 且声速为340m/s, 求炮弹爆炸点的轨迹方程.
【例2】
[ 探究 ]
【拓展练习】
【练习1】
【练习2】
与圆(x+3)2+y2=1及圆(x-3)2+y2=9都外切的圆的圆心在( )
A. 一个椭圆上
B. 双曲线的一支上
C. 一条抛物线上
D. 一个圆上
【练习3】
1. 双曲线的标准方程的外在形式与其焦点所在坐标轴有关,由双曲线方程分析有关性质,一般先将其方程化为标准方程,再确定a、b、c的值.
2. 求双曲线标准方程时,若不知焦点所在坐标轴, 可设双曲线方程为Ax2+By2=1,用代定系数法求解.
《考一本》第14课时
【练习4】
【练习5】
