六年级下册青岛版数学 总复习——二图形与几何 2.图形的位置与运动(课件)(共35张PPT)
文档属性
| 名称 | 六年级下册青岛版数学 总复习——二图形与几何 2.图形的位置与运动(课件)(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 06:45:34 | ||
图片预览







文档简介
(共35张PPT)
青岛版数学六年级(下)
二 图形与几何
2.图形的位置与运动
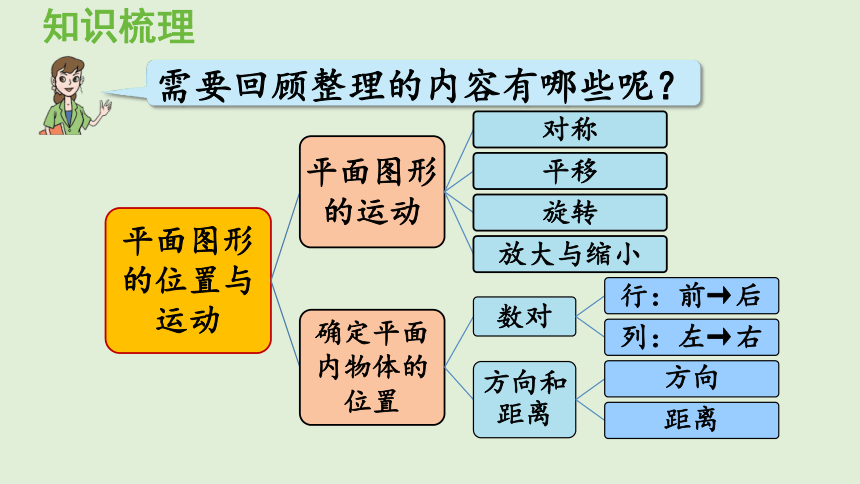
知识梳理
需要回顾整理的内容有哪些呢?
问题导入
我们学过哪些关于图形的运动的知识?
平移
旋转
放大
缩小
轴对称
平移、旋转和轴对称不改变图形的形状和大小。
图形的放大和缩小只改变图形的大小不改变形状。
哪些运动不改变图形的形状和大小?
哪些运动只改变图形的大小,而不改变形状?
要点回顾
知识点1:平面图形的运动
对称
对称现象是指生活中一个物体(包括建筑物,生活用品,学习工具……)上下或左右两部分能够完全重合的现象。
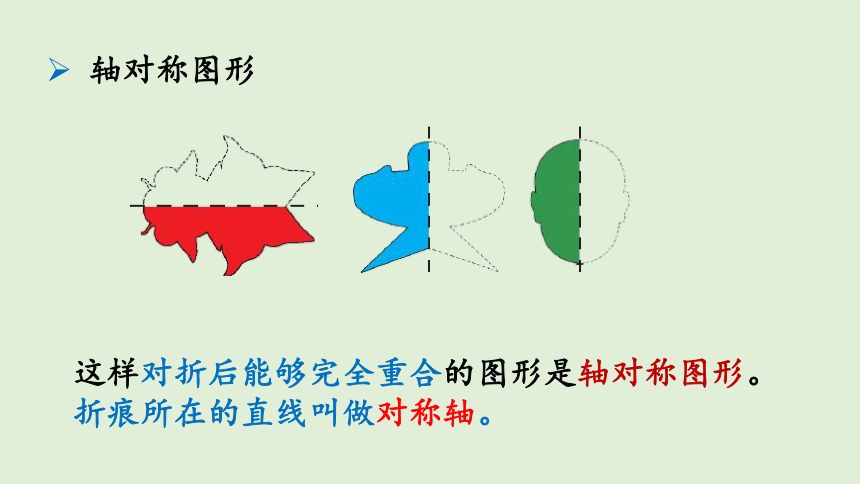
轴对称图形
这样对折后能够完全重合的图形是轴对称图形。折痕所在的直线叫做对称轴。
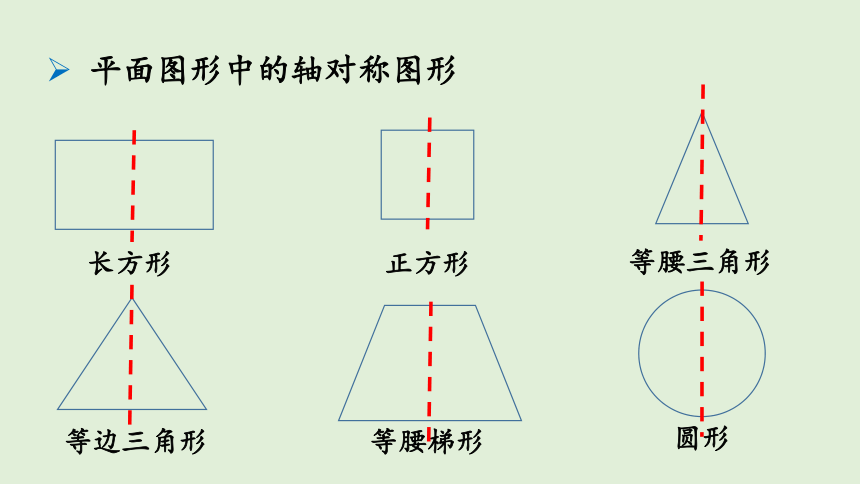
平面图形中的轴对称图形
长方形
正方形
等边三角形
等腰梯形
等腰三角形
圆形
平移
图形的平移 意义
要素
特点
画法
在同一平面内,将一个图形沿一直线移动一定的距离,这样的图形运动叫做平移。
平移的方向、平移的距离。
只改变图形的位置,不改变图形的形状、大小及方向。
先找出图形的关键点,再按要求平移相应的距离,最后把这些点顺次连接起来。
旋转
图形的旋转 意义
要素
特点
画法
在平面内,将一个图形绕一个点按某个方向转动一个角度,这样的图形运动叫做旋转。
旋转中心、旋转方向、旋转角度。
图形的位置、方向都改变了,但形状和大小都不变。
先找准旋转中心,然后确定旋转的方向和旋转的角度,再分别旋转各边,最后画出各边的对应边。
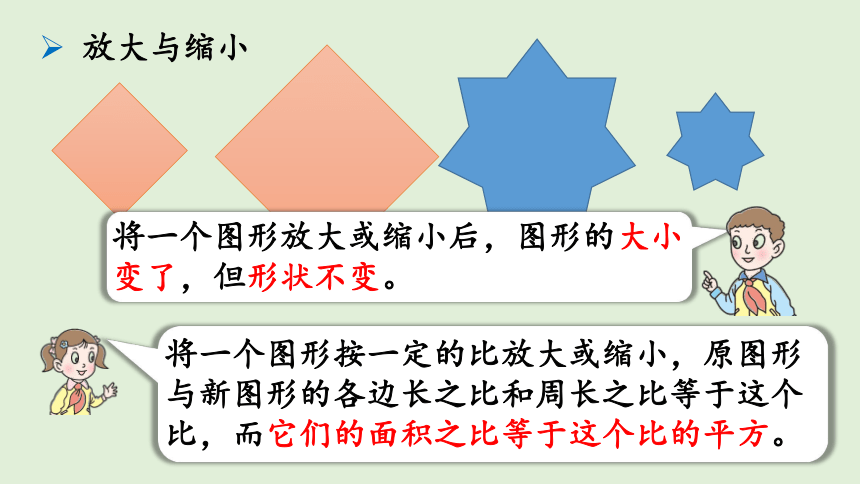
放大与缩小
将一个图形按一定的比放大或缩小,原图形与新图形的各边长之比和周长之比等于这个比,而它们的面积之比等于这个比的平方。
将一个图形放大或缩小后,图形的大小变了,但形状不变。
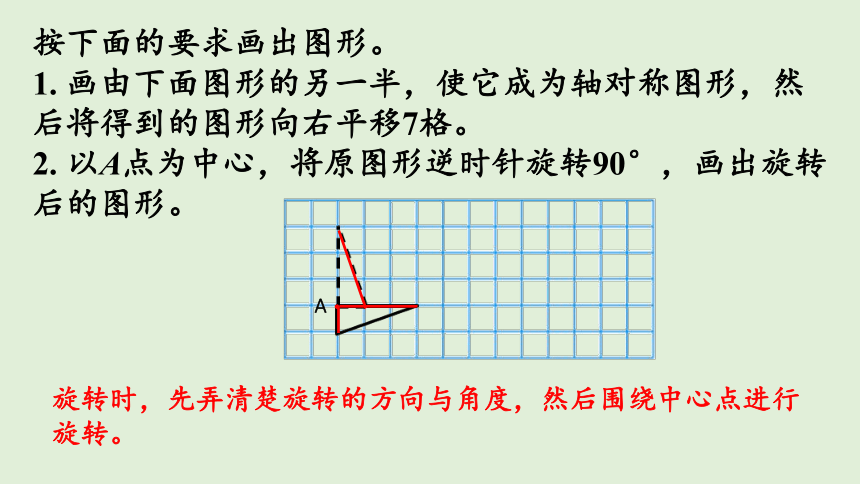
按下面的要求画出图形。
1. 画由下面图形的另一半,使它成为轴对称图形,然后将得到的图形向右平移7格。
2. 以A点为中心,将原图形逆时针旋转90°,画出旋转后的图形。
●
●
画图形的另一半时,先确定各对称点的位置,再连线。
●
按下面的要求画出图形。
1. 画由下面图形的另一半,使它成为轴对称图形,然后将得到的图形向右平移7格。
2. 以A点为中心,将原图形逆时针旋转90°,画出旋转后的图形。
画平移后的图形时,先确定各关键点平移后的位置,再连线。
旋转时,先弄清楚旋转的方向与角度,然后围绕中心点进行旋转。
A
按下面的要求画出图形。
1. 画由下面图形的另一半,使它成为轴对称图形,然后将得到的图形向右平移7格。
2. 以A点为中心,将原图形逆时针旋转90°,画出旋转后的图形。
知识点2:确定平面内物体的位置
(1)确定观测点,画出以观测点为中心的正北、正南、正西、正东四个方向的射线。
(2)把观测点和观察目标连起来,与南北(东西)方向形成一个角,测量出该角的度数。
(3)测量出观测点和观测目标的图上距离,根据比例尺与图上距离计算出实际距离。
(4)根据方向和距离两个条件就能精确地确定平面内物体的位置。
用方向和距离确定物体的位置
灯塔
200米
45°
A
如果知道了方向与距离,可以确定它的位置。例如:A点在灯塔的北偏东45°方向200米处,那么它的位置就可以如图这样来确定。
A
(3,3)
先列(竖排)后行(横排),用小括号把列数和行数相对应的数字括起来,并用逗号隔开,即(列数,行数)。
用数对表示物体的位置
如果知道物体在第几列第几行,可以用数对来确定它的位置。例如: A点的位置在第3列,第3行,就可以表示为(3,3)。
根据方向和距离描述行走路线
1.根据方向标明确路线图的方向。
2.清楚路线图中所经过的场所和各场所的顺序及角度、方向。
3.明确每两个场所之间的距离。
4.用“从”“到达”“然后”“最后”等词语说清从哪里出发,向什么方向,走多远,到达哪里。
课堂练习
1.图中A→B→C→D是怎样变过来的?
向右平移5格
A
B
C
D
先向右平移5格,再绕中心逆时针旋转90°
先向右平移5格,再绕中心逆时针旋转90°
(1)风车转动是( )现象,推拉窗户是( )现象。(填“平移”或“旋转”)
旋转
平移
沿直线移动一定的距离。
2.填一填。
绕中心点逆时针转动360°。
(2)把一个边长为10厘米的正方形按3∶1放大,放大后所得图形的面积是( )平方厘米。
900
可以先求出放大后的边长再求放大后的面积;也可以先求出放大前的面积再求放大后的面积。
方法一:(10×3)2=900(cm2)
方法二:10×10×32=900(cm2)
(3)一个底面直径是4厘米、高是3厘米的圆柱,放大后底面的周长是62.8厘米,这个圆柱是按( )放大了,放大后的圆柱的底面积是( )平方厘米。
5∶1
314
放大后的底面直径:62.8÷3.14=20(cm)
放大后与放大前的比:20∶4=5∶1
放大后的底面积:3.14×(20÷2)2=314(cm2)
( )条
对称轴
( )条
对称轴
2
( )条
对称轴
(4)数一数,下面每幅图有几条对称轴?
无数
( )条
对称轴
0
5
(1)下面物体的运动方式中,( )与其他三种运动方式不同。
A.螺旋桨的运动
B.抽屉的拉动
C.风扇叶片的转动
D.钟摆的摆动
B
旋转
平移
旋转
旋转
3.选一选。
(2)将一张正方形纸片沿虚线向上对折,再沿虚线向右对折,得到一个正方形,然后剪下一个角,如下图所示。将这张纸片展开后应该是( )。
B
A
B
C
D
(3)下列各图形面积计算公式的推导过程中,没有用到平移或旋转的是( )。
A.三角形
B.梯形
C.圆
D.平行四边形
C
旋转、平移
旋转、平移
剪拼
割补、平移
4.操作题。
(1)将图中A图形先向( )平移( )格,再向( )平移( )格,就能和B图形拼成一个正方形。
O
·
A
B
右 4
下 2
右 4
下 2
4.操作题。
(2)在图中画出B图形绕点O逆时针旋转90°后的图形。
O
·
A
B
B
(3)按2∶1的比画出B图形放大后的图形。
5.你能画出下面轴对称图形的另一半吗?
·
·
·
·
·
·
·
·
·
·
·
·
先找出已知图形的几个关键点,在对称轴的另一侧找出它们的对称点,按已知图形形状连接各对称点,就画出了轴对称图形的另一半。
生活中描述物体位置时,需要用到方向与距离。
教材第110页“应用与反思”第1题
6.右面是从公园到商店的路线图。
(1)从公园到商店怎么走
(2)说说从商店到桃园的路线。
公园
东
1500m
桃园
南
900m
书城
东南
600m
电信局
东
400m
商店
商店
西
400m
电信局
西北
600m
书城
北
600m
桃园
教材第110页“应用与反思”第2题
7.如果渔船在海上遇难,应该向救援中心发送下面的哪条信息才能及时获救 说说你的理由。
(1)我们的船在牛山岛的东北方向。
(2)我们的船在牛山岛的东北方向40千米处。
(3)我们的船在牛山岛的北偏东50°方向40千米处。
渔船
北
50°
牛山岛
10km
怎样准确有效地传递求救信息
教材第110页“应用与反思”第2题
7.如果渔船在海上遇难,应该向救援中心发送下面的哪条信息才能及时获救 说说你的理由。
(3)我们的船在牛山岛的北偏东50°方向40千米处。
渔船
北
50°
牛山岛
10km
第(3)条信息。
理由:这条信息有明确的参照
物、渔船在参照物的方向以及
距离,根据这些信息才能够快速地找到渔船的位置,实施救援。
教材第110页“应用与反思”第3题
8.
1
2
3
4
5
6
7
1
2
3
4
5
0
6
书店
影院
超市
学校
医院
(1)学校的位置用数对表示为( )。
(2)邮局的位置为(5, 3),你能在图上表示出来吗
(3)怎样用数对表示其他场所的位置呢
1 , 2
邮局
超市:(2 , 3)
医院:(3 , 1)
影院:(4 , 4)
书店:(6 , 5)
9.如下图,以电视塔为观测点,填一填。
(1)市民广场在电视塔的( )方向( )米处。
正东
0 80 160 240米
北
电信大楼
市民广场
电视塔
少年宫
30°
·
40°
(2)电信大楼在电视塔的( )偏( )( )°方向( )米处。
160
(3)少年宫在电视塔的( )偏( )( )°方向( )米处。
北
40
东
240
南
30
西
240
电信业务,她首先要从市民广场往( )方向步行( )米到达电视塔,再往( )偏( )( )°方向行( )米即可到达。
正西
(2)王阿姨的家住在市民广场附近,一天早晨,她打算从市民广场出发,步行经过电视塔去电信大楼办理
0 80 160 240米
北
电信大楼
市民广场
电视塔
少年宫
30°
·
40°
160
北
40
东
240
·
从“市民广场”出发时观测点是“市民广场”。
从“电视塔”出发时观测点是“电视塔”。
0
9
10.如下图,平行四边形ABCD的三个顶点A、B、C的位置用数对表示分别是(4,6)、(1,3)、(5,3),那么顶点D的位置用数对表示为( )。
8,6
4
6
1
3
5
2
3
8
6
7
4格
1
2
4
5
7
D
C
B
A
4格
根据已知的三个顶点的数对画出带刻度的方格纸,就可以用数对表示出D点的位置。
作业课件中的相关练习。
02
01
课后练习题。
课后作业
青岛版数学六年级(下)
二 图形与几何
2.图形的位置与运动
知识梳理
需要回顾整理的内容有哪些呢?
问题导入
我们学过哪些关于图形的运动的知识?
平移
旋转
放大
缩小
轴对称
平移、旋转和轴对称不改变图形的形状和大小。
图形的放大和缩小只改变图形的大小不改变形状。
哪些运动不改变图形的形状和大小?
哪些运动只改变图形的大小,而不改变形状?
要点回顾
知识点1:平面图形的运动
对称
对称现象是指生活中一个物体(包括建筑物,生活用品,学习工具……)上下或左右两部分能够完全重合的现象。
轴对称图形
这样对折后能够完全重合的图形是轴对称图形。折痕所在的直线叫做对称轴。
平面图形中的轴对称图形
长方形
正方形
等边三角形
等腰梯形
等腰三角形
圆形
平移
图形的平移 意义
要素
特点
画法
在同一平面内,将一个图形沿一直线移动一定的距离,这样的图形运动叫做平移。
平移的方向、平移的距离。
只改变图形的位置,不改变图形的形状、大小及方向。
先找出图形的关键点,再按要求平移相应的距离,最后把这些点顺次连接起来。
旋转
图形的旋转 意义
要素
特点
画法
在平面内,将一个图形绕一个点按某个方向转动一个角度,这样的图形运动叫做旋转。
旋转中心、旋转方向、旋转角度。
图形的位置、方向都改变了,但形状和大小都不变。
先找准旋转中心,然后确定旋转的方向和旋转的角度,再分别旋转各边,最后画出各边的对应边。
放大与缩小
将一个图形按一定的比放大或缩小,原图形与新图形的各边长之比和周长之比等于这个比,而它们的面积之比等于这个比的平方。
将一个图形放大或缩小后,图形的大小变了,但形状不变。
按下面的要求画出图形。
1. 画由下面图形的另一半,使它成为轴对称图形,然后将得到的图形向右平移7格。
2. 以A点为中心,将原图形逆时针旋转90°,画出旋转后的图形。
●
●
画图形的另一半时,先确定各对称点的位置,再连线。
●
按下面的要求画出图形。
1. 画由下面图形的另一半,使它成为轴对称图形,然后将得到的图形向右平移7格。
2. 以A点为中心,将原图形逆时针旋转90°,画出旋转后的图形。
画平移后的图形时,先确定各关键点平移后的位置,再连线。
旋转时,先弄清楚旋转的方向与角度,然后围绕中心点进行旋转。
A
按下面的要求画出图形。
1. 画由下面图形的另一半,使它成为轴对称图形,然后将得到的图形向右平移7格。
2. 以A点为中心,将原图形逆时针旋转90°,画出旋转后的图形。
知识点2:确定平面内物体的位置
(1)确定观测点,画出以观测点为中心的正北、正南、正西、正东四个方向的射线。
(2)把观测点和观察目标连起来,与南北(东西)方向形成一个角,测量出该角的度数。
(3)测量出观测点和观测目标的图上距离,根据比例尺与图上距离计算出实际距离。
(4)根据方向和距离两个条件就能精确地确定平面内物体的位置。
用方向和距离确定物体的位置
灯塔
200米
45°
A
如果知道了方向与距离,可以确定它的位置。例如:A点在灯塔的北偏东45°方向200米处,那么它的位置就可以如图这样来确定。
A
(3,3)
先列(竖排)后行(横排),用小括号把列数和行数相对应的数字括起来,并用逗号隔开,即(列数,行数)。
用数对表示物体的位置
如果知道物体在第几列第几行,可以用数对来确定它的位置。例如: A点的位置在第3列,第3行,就可以表示为(3,3)。
根据方向和距离描述行走路线
1.根据方向标明确路线图的方向。
2.清楚路线图中所经过的场所和各场所的顺序及角度、方向。
3.明确每两个场所之间的距离。
4.用“从”“到达”“然后”“最后”等词语说清从哪里出发,向什么方向,走多远,到达哪里。
课堂练习
1.图中A→B→C→D是怎样变过来的?
向右平移5格
A
B
C
D
先向右平移5格,再绕中心逆时针旋转90°
先向右平移5格,再绕中心逆时针旋转90°
(1)风车转动是( )现象,推拉窗户是( )现象。(填“平移”或“旋转”)
旋转
平移
沿直线移动一定的距离。
2.填一填。
绕中心点逆时针转动360°。
(2)把一个边长为10厘米的正方形按3∶1放大,放大后所得图形的面积是( )平方厘米。
900
可以先求出放大后的边长再求放大后的面积;也可以先求出放大前的面积再求放大后的面积。
方法一:(10×3)2=900(cm2)
方法二:10×10×32=900(cm2)
(3)一个底面直径是4厘米、高是3厘米的圆柱,放大后底面的周长是62.8厘米,这个圆柱是按( )放大了,放大后的圆柱的底面积是( )平方厘米。
5∶1
314
放大后的底面直径:62.8÷3.14=20(cm)
放大后与放大前的比:20∶4=5∶1
放大后的底面积:3.14×(20÷2)2=314(cm2)
( )条
对称轴
( )条
对称轴
2
( )条
对称轴
(4)数一数,下面每幅图有几条对称轴?
无数
( )条
对称轴
0
5
(1)下面物体的运动方式中,( )与其他三种运动方式不同。
A.螺旋桨的运动
B.抽屉的拉动
C.风扇叶片的转动
D.钟摆的摆动
B
旋转
平移
旋转
旋转
3.选一选。
(2)将一张正方形纸片沿虚线向上对折,再沿虚线向右对折,得到一个正方形,然后剪下一个角,如下图所示。将这张纸片展开后应该是( )。
B
A
B
C
D
(3)下列各图形面积计算公式的推导过程中,没有用到平移或旋转的是( )。
A.三角形
B.梯形
C.圆
D.平行四边形
C
旋转、平移
旋转、平移
剪拼
割补、平移
4.操作题。
(1)将图中A图形先向( )平移( )格,再向( )平移( )格,就能和B图形拼成一个正方形。
O
·
A
B
右 4
下 2
右 4
下 2
4.操作题。
(2)在图中画出B图形绕点O逆时针旋转90°后的图形。
O
·
A
B
B
(3)按2∶1的比画出B图形放大后的图形。
5.你能画出下面轴对称图形的另一半吗?
·
·
·
·
·
·
·
·
·
·
·
·
先找出已知图形的几个关键点,在对称轴的另一侧找出它们的对称点,按已知图形形状连接各对称点,就画出了轴对称图形的另一半。
生活中描述物体位置时,需要用到方向与距离。
教材第110页“应用与反思”第1题
6.右面是从公园到商店的路线图。
(1)从公园到商店怎么走
(2)说说从商店到桃园的路线。
公园
东
1500m
桃园
南
900m
书城
东南
600m
电信局
东
400m
商店
商店
西
400m
电信局
西北
600m
书城
北
600m
桃园
教材第110页“应用与反思”第2题
7.如果渔船在海上遇难,应该向救援中心发送下面的哪条信息才能及时获救 说说你的理由。
(1)我们的船在牛山岛的东北方向。
(2)我们的船在牛山岛的东北方向40千米处。
(3)我们的船在牛山岛的北偏东50°方向40千米处。
渔船
北
50°
牛山岛
10km
怎样准确有效地传递求救信息
教材第110页“应用与反思”第2题
7.如果渔船在海上遇难,应该向救援中心发送下面的哪条信息才能及时获救 说说你的理由。
(3)我们的船在牛山岛的北偏东50°方向40千米处。
渔船
北
50°
牛山岛
10km
第(3)条信息。
理由:这条信息有明确的参照
物、渔船在参照物的方向以及
距离,根据这些信息才能够快速地找到渔船的位置,实施救援。
教材第110页“应用与反思”第3题
8.
1
2
3
4
5
6
7
1
2
3
4
5
0
6
书店
影院
超市
学校
医院
(1)学校的位置用数对表示为( )。
(2)邮局的位置为(5, 3),你能在图上表示出来吗
(3)怎样用数对表示其他场所的位置呢
1 , 2
邮局
超市:(2 , 3)
医院:(3 , 1)
影院:(4 , 4)
书店:(6 , 5)
9.如下图,以电视塔为观测点,填一填。
(1)市民广场在电视塔的( )方向( )米处。
正东
0 80 160 240米
北
电信大楼
市民广场
电视塔
少年宫
30°
·
40°
(2)电信大楼在电视塔的( )偏( )( )°方向( )米处。
160
(3)少年宫在电视塔的( )偏( )( )°方向( )米处。
北
40
东
240
南
30
西
240
电信业务,她首先要从市民广场往( )方向步行( )米到达电视塔,再往( )偏( )( )°方向行( )米即可到达。
正西
(2)王阿姨的家住在市民广场附近,一天早晨,她打算从市民广场出发,步行经过电视塔去电信大楼办理
0 80 160 240米
北
电信大楼
市民广场
电视塔
少年宫
30°
·
40°
160
北
40
东
240
·
从“市民广场”出发时观测点是“市民广场”。
从“电视塔”出发时观测点是“电视塔”。
0
9
10.如下图,平行四边形ABCD的三个顶点A、B、C的位置用数对表示分别是(4,6)、(1,3)、(5,3),那么顶点D的位置用数对表示为( )。
8,6
4
6
1
3
5
2
3
8
6
7
4格
1
2
4
5
7
D
C
B
A
4格
根据已知的三个顶点的数对画出带刻度的方格纸,就可以用数对表示出D点的位置。
作业课件中的相关练习。
02
01
课后练习题。
课后作业
