六年级下册青岛版数学 总复习——2.数的运算第3课时 解决实际问题(课件)(共45张PPT)
文档属性
| 名称 | 六年级下册青岛版数学 总复习——2.数的运算第3课时 解决实际问题(课件)(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 00:00:00 | ||
图片预览









文档简介
(共45张PPT)
第3课时 解决实际问题
青岛版数学六年级(下)
一 数与代数
2.数的运算
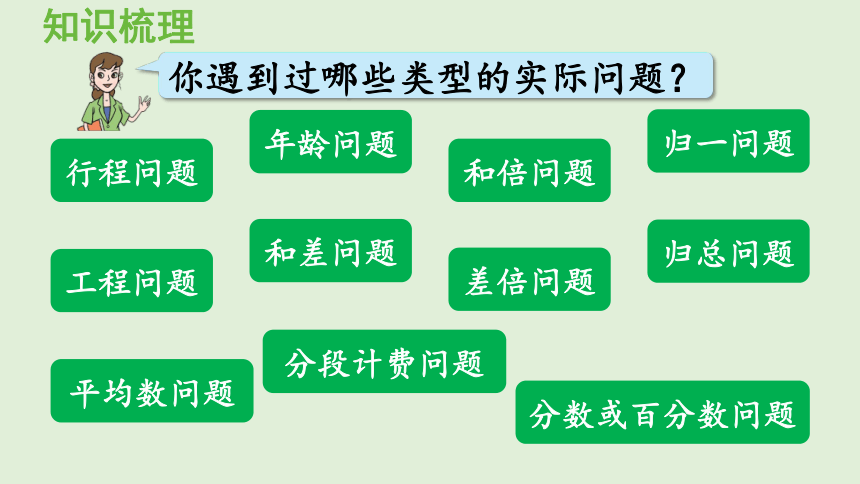
平均数问题
归一问题
归总问题
行程问题
和倍问题
差倍问题
和差问题
年龄问题
分段计费问题
分数或百分数问题
工程问题
知识梳理
你遇到过哪些类型的实际问题?
阅读与理解:读题,理解题意,明确已知条件和所求问题。
分析与解答:先分析数量关系,确定怎样算,再列式计算。
回顾与反思:反思解题过程,验证答案是否正确,并写出答语。
通过计算可以解决许多实际问题,解决实际问题时有哪些主要步骤?
综合法
分析法
综合分析法
又叫顺推法,从已知信息入手“由因导果”,推想到问题。
又叫逆推法,从问题着手“执因索果”,推想到已知信息。
将综合法与分析法结合起来交替使用的方法。
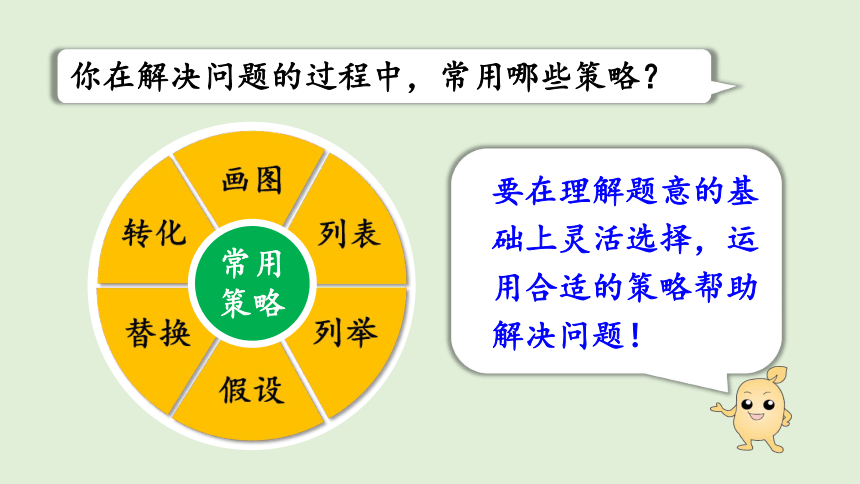
你在解决问题的过程中,常用哪些策略?
画图
列表
列举
假设
替换
转化
常用策略
要在理解题意的基础上灵活选择,运用合适的策略帮助解决问题!
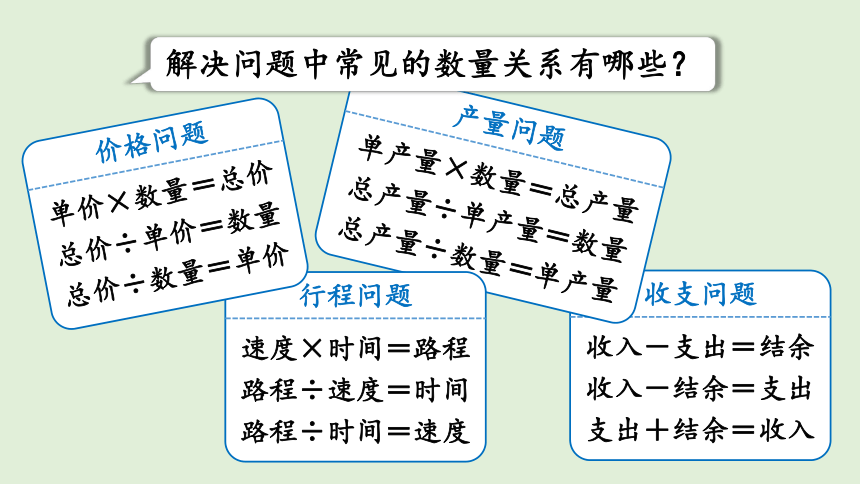
收入-支出=结余
收入-结余=支出
支出+结余=收入
收支问题
单产量×数量=总产量
总产量÷单产量=数量
总产量÷数量=单产量
产量问题
速度×时间=路程
路程÷速度=时间
路程÷时间=速度
行程问题
单价×数量=总价
总价÷单价=数量
总价÷数量=单价
价格问题
解决问题中常见的数量关系有哪些?
分数或百分数问题
(1)求甲数是乙数的几(百)分之几。
甲数÷乙数=甲数是乙数的几(百)分之几
(2)已知甲数是乙数的几(百)分之几,求甲数。
乙数×几(百)分之几=甲数
(3)已知甲数是乙数的几(百)分之几,求乙数。
甲数÷几(百)分之几=乙数
分数或百分数问题
(4)求甲数比乙数多(少)几(百)分之几。
两个数的差÷乙数=
甲数比乙数多(少)的几(百)分之几
(5)已知甲数比乙数多(少)几(百)分之几,求甲数。
乙数×[1±几(百)分之几]=甲数
(6)已知甲数比乙数多(少)几(百)分之几,求乙数。
甲数÷[1±几(百)分之几]=乙数
折扣问题、成数问题、纳税问题、储蓄问题都可以转化为一般的百分数问题来分析解答。
折扣问题
成数问题
储蓄问题
纳税问题
现价÷折扣=原价
现价÷原价=折扣
几成就是十分之几,也就是百分之几十。
应纳税所得额×税率=应纳税额
利息=本金×利率×存期
原价×折扣=现价
行程问题
两个物体从两地出发,相向而行,经过一段时间后相遇。
两个物体同时不同地(或同地不同时或不同地不同时)出发,同向而行,后面的物体的速度快,在一定时间内能追上前面物体。
相遇问题
追及问题
题中每份的量保持不变,解题时先求出不变的单一量,再求出未知量。
主要是研究工作总量、工作时间和工作效率三者之间关系问题。
工作总量=工作效率×工作时间
解题时,通常把工作总量看成单位“1”。
归一问题
工程问题
此类题蕴含着“总量”不变,解题时,先求出总量,再求出未知量。
归总问题
已知大、小两个数的和与差,求这两个数分别是多少。
已知两个数的差及这两个数的倍数关系,求这两个数分别是多少。
和差问题
差倍问题
已知两个数的和及这两个数的倍数关系,求这两个数分别是多少。
和倍问题
王老师要买190本《数学小词典》,单价是3.80元/本。她带了800元钱,够吗?应找回(或再付)多少元?
根据解决问题的需要,怎样选择合理的计算方法?
从题中,你知道了哪些数学信息?
每本3.8元
要买190本
1.怎样选择合理的计算方法?
2.怎样解决“带了800元钱,够吗?”这个问题。
一
想
想
3. 8 0
× 1 9 0
3 4 2
3 8 0
7 2 2. 0 0
3.80 ×190
=722 (元)
722 <800
答:带800元钱够了。
笔算可以解决这个问题。
方法一
每本3.8元
要买190本
方法二
用简便方法口算解决这个问题。
3.80 ×190
= 722 (元)
722 <800
答:带800元钱够了。
3.80 × 190
= 3.80 × 200 - 3.80 × 10
= 760 - 38
= 722(元)
每本3.8元
要买190本
方法三
用计算器计算也可以解决这个问题。
722 < 800
答:带800元钱够了。
3.80 ×190
722 (元)
=
每本3.8元
要买190本
要解决的问题是“带了800元钱够吗?”,不需要求出精确的结果,求近似值即可,所以用估算就可以解决。
方法四
每本3.8元
要买190本
用估算可以解决这个问题。
3.80 ×190
答:带800元钱够了。
3.80 ≈ 4
4×200 = 800(元)
190 ≈ 200
≈800(元)
想一想,在选择计算方法解决问题的过程中,我们经历了怎样一个过程?
问题情境
王老师买词典
需要计算
带了800元钱,够吗?
应找回(或再付)多少元?
只需要近似值
需要精确值
估算
3.80≈4
190≈200
4×200=800
口算
3.80×200-3.80×10
笔算
3. 8 0
× 1 9 0
用计算器算
3.80×190
计算比较简单,能够快速解决问题
计算结果精确,但过程相对较为复杂。
计算过程简便、快捷,结果精确,但计算器携带不便。
如图,要为这样一个饮料罐的外壁制作标签纸,至少需要多少纸?
5×3.14×14
= 219.8(平方厘米)
这里用到了小数乘法计算。
“图形与几何”“统计与可能性”等知识的学习是不是也要用到计算?谈谈你的看法。
再如:六年级一周30节课,各学科课时占总课时的百分比如下图。一周有多少节语文课?
30×23.3%≈7(节)
计算在数学学习中非常重要,大部分的知识要用到计算。
这里用到了分数乘法计算。
课堂练习
1.小刚和小明分别从书店和学校同时出发去体育馆。小刚平均每分钟走60米。如果两人要同时到达,小明平均每分钟要走多少米
360÷60=6(分)
240÷6=40(米)
答:小明平均每分钟走40米。
360米
240米
教材第91页“应用与反思”第7题
“两人同时到达体育馆”表示两人走的时间是一样的,先根据“时间=路程(360)÷速度(60)”求出所需时间,再根据“速度=路程(240)÷时间”求出小明的速度。
2.一列火车从A城开往B城。如果速度是120千米/时,则4小时可以到达;如果速度是160千米/时,几小时可以到达
120×4÷160=3(时)
答:3小时可以到达。
教材第91页“应用与反思”第8题
先求出路程,路程是不变量,再根据“时间=路程÷速度”求出提速后所需的时间。
教材第91页“应用与反思”第9题
3.学校食堂计划购买1500千克大米。
(1)如果平均每天吃95千克,这些大米够吃半个月吗 (一个月按30天计算)
(2)如果够了,还剩下多少千克 如果不够,还需要购进多少千克
要解答“这些大米够不够吃半个月”的问题,需要估算还是精确计算
要解答“剩下多少千克”或“需要购进多少千克”的问题呢
3.学校食堂计划购买1500千克大米。
(1)如果平均每天吃95千克,这些大米够吃半个月吗 (一个月按30天计算)
这些大米
够吃半个
月吗?
只需要
近似值
估算:95≈100
100×15=1500(千克)
答:够了。
教材第91页“应用与反思”第9题
因为把95估成100时,数变大了,所以估算的积大于实际的积,也就是说实际半个月吃不了1500千克大米。因此,这些大米够吃半个月。
3.学校食堂计划购买1500千克大米。
(2)如果够了,还剩下多少千克 如果不够,还需要购进多少千克
教材第91页“应用与反思”第9题
还剩下(还
需要购进)
多少千克?
需要精
确计算
先求半个月需要多少千克大米:
95×(30÷2)=1425(千克)
再求还剩下多少千克:
1500-1425=75(千克)
答:还剩下75千克。
教材第91页“应用与反思”第10题
4.下面是王阿姨某天卖出报刊情况记录表。
(1)《都市晚报》和《京华晨报》一共卖了多少元
单件(元) 数量
《都市晚报》 0.50 90份
《京华晨报》 0.30 85份
《电脑世界》 1.85 25本
《城市生活》 5.70 9本
总价=单价×数量
(1)0.50×90+0.30×85=70.50(元)
答:一共卖了70.5元。
4.下面是王阿姨某天卖出报刊情况记录表。
单件(元) 数量
《都市晚报》 0.50 90份
《京华晨报》 0.30 85份
《电脑世界》 1.85 25本
《城市生活》 5.70 9本
(2) 《电脑世界》和《城市生活》哪种卖的钱多 多多少元
教材第91页“应用与反思”第10题
总价=单价×数量
(2)《电脑世界》:1.85×25=46.25(元)
《城市生活》:5.70×9=51.30(元) 46.25<51.30
51.30-46.25=5.05(元)
答:《城市生活》卖的钱多,比《电脑世界》多5.05元。
教材第92页“应用与反思”第11题
5.青山小学六年级有学生126人,报名参加冬季越野比赛的占,其中男生占。参加越野比赛的男生有多少人
答:参加越野比赛的男生有70人。
126××=70(人)
先求报名冬季越野比赛的学生有多少,用总人数乘;再求其中的男生有多少人,用上一步的结果乘,即可解决问题。
教材第92页“应用与反思”第12题
6.你知道动物的牙齿数吗 猫有30颗,马有36颗,兔有28颗,狗的牙齿数比猫的多,大象的牙齿数只相当于马的。
请根据上面的信息填表。
动物 猫 马 兔 狗 大象
牙齿数(颗)
30
36
28
42
6
猫的牙齿数×+猫的牙齿数
马的牙齿数×
教材第92页“应用与反思”第13题
7. (1)质监局对全市儿童服装产品进行质量抽检。在抽检的产品中有48个品牌产品合格,有2个品牌产品不合格。本次抽检的合格率是多少
48÷(48+2)×100%=96%
答:本次抽检的合格率是96%。
合格率=合格数÷总数
教材第92页“应用与反思”第13题
8. (2)大豆的出油率是18%。现有250千克大豆,能榨出50千克豆油吗
250×18%=45(千克)
45<50
答:250千克大豆不能榨出50千克豆油。
榨出的油的质量=大豆的质量×出油率
教材第92页“应用与反思”第14题
9.一种“感冒通”片的两种主要药物成分是人工牛黄( 12%)和马来酸氯苯那敏( 2%)。制药厂要配制5000克这样的“感冒通”片,这两种药物分别需要多少克
解决上面的问题需要精确计算吗
需要
人工牛黄:5000×12%=600(克)
马来酸氯苯那敏:5000×2%=100(克)
教材第93页“应用与反思”第16题
10. 大连、烟台两个港口相距87海里。 甲、乙两船分别从两个港口同时出发,相向而行,3小时后相遇。乙船每小时行15海里,甲船每小时行多少海里
87÷3-15=14(海里)
答:甲船每小时行驶14海里。
所求问题是“甲船每小时行多少海里?”,需要求出确切的速度,所以要精确计算。
速度和=路程÷相遇时间
教材第93页“应用与反思”第17题
11.
(1) 2017年1月9日,王平的爸爸在银行存了20000元钱,定期一年,年利率是1.75%。 到期后应得利息多少元
20000×1.75%×1=350(元)
答:到期后应得利息350元。
利息=本金×利率×存期
教材第93页“应用与反思”第17题
(2)一种上衣原价为120元,现按七折销售,便宜了多少元
120-120×70%=36(元)
答:便宜了36元。
几折就是十分之几,也就是百分之几十。
原价×折扣=现价
教材第93页“应用与反思”第17题
(3)商场12月份销售的女装数量比男装多25%,男装销售了1280件,女装销售了多少件
1280×(1+25%)=1600(件)
答:女装销售了1600件。
男装销售件数×25%=女装比男装多销售的件数
女装销售件数=男装销售件数+女装比男装多销售的件数
教材第93页“应用与反思”第18题
12. 李大爷家养的鸡、鸭、鹅共3000只。
3000×30%-3000×18%=360(只)
答:鸭比鹅多360只。
鸭比鹅多多少只
教材第93页“应用与反思”第19题
13.河东区要修一条640米的景观大道,第一周修了这条路的第二周修了这条路的20%,还剩多少米没修
640-640× - 640×20%=352(米)
答:还剩下352米没有修。
教材第93页“应用与反思”第20题
14.下表是A、B、C三个城市绿化面积的有关信息。
城市 A B C
总面积(万平方千米) 0.7 1.1 1.5
绿化面积(万平方千米) 0.23 0.25 0.27
哪个城市的绿化情况好一些?
直接比较绿化面积能反映三个城市的绿化情况吗
应该比较它们的绿化率.....
教材第93页“应用与反思”第20题
因为A、B、C三个城市的总面积不同,所以直接比较绿化面积不能反映三个城市的绿化情况,应该比较它们的绿化率。
答:A城市的绿化情况好一些。
32.9%>22.7%>18%
A城市:0.23÷0.7×100%≈32.9%
B城市:0.25÷1.1×100%≈22.7%
C城市:0.27÷1.5×100%≈18%
教材第93页“应用与反思”第21题
15.超市有鸡蛋40箱、鸭蛋30箱,共重275千克。已知1箱鸡蛋的质量和2箱鸭蛋的质量相等,1箱鸡蛋的质量是多少千克
1箱鸭蛋的质量:275÷(40×2+30)=2.5(千克)
1箱鸡蛋的质量:2.5×2=5(千克)
答:一箱鸡蛋的质量是5千克。
假设全部是鸭蛋,则鸭蛋共有( 40×2+30 )箱,根据 “总质量÷箱数=1箱的质量”先求出1箱鸭蛋的质量。
思路一
教材第93页“应用与反思”第21题
15.超市有鸡蛋40箱、鸭蛋30箱,共重275千克。已知1箱鸡蛋的质量和2箱鸭蛋的质量相等,1箱鸡蛋的质量是多少千克
1箱鸡蛋的质量:275÷(40+30÷2)=5(千克)
答:一箱鸡蛋的质量是5千克。
假设全部是鸡蛋,则鸡蛋共有( 40+30÷2 )箱,根据 “总质量÷箱数=1箱的质量”求出1箱鸡蛋的质量。
思路二
相关练习。
02
01
课后练习题。
课后作业
第3课时 解决实际问题
青岛版数学六年级(下)
一 数与代数
2.数的运算
平均数问题
归一问题
归总问题
行程问题
和倍问题
差倍问题
和差问题
年龄问题
分段计费问题
分数或百分数问题
工程问题
知识梳理
你遇到过哪些类型的实际问题?
阅读与理解:读题,理解题意,明确已知条件和所求问题。
分析与解答:先分析数量关系,确定怎样算,再列式计算。
回顾与反思:反思解题过程,验证答案是否正确,并写出答语。
通过计算可以解决许多实际问题,解决实际问题时有哪些主要步骤?
综合法
分析法
综合分析法
又叫顺推法,从已知信息入手“由因导果”,推想到问题。
又叫逆推法,从问题着手“执因索果”,推想到已知信息。
将综合法与分析法结合起来交替使用的方法。
你在解决问题的过程中,常用哪些策略?
画图
列表
列举
假设
替换
转化
常用策略
要在理解题意的基础上灵活选择,运用合适的策略帮助解决问题!
收入-支出=结余
收入-结余=支出
支出+结余=收入
收支问题
单产量×数量=总产量
总产量÷单产量=数量
总产量÷数量=单产量
产量问题
速度×时间=路程
路程÷速度=时间
路程÷时间=速度
行程问题
单价×数量=总价
总价÷单价=数量
总价÷数量=单价
价格问题
解决问题中常见的数量关系有哪些?
分数或百分数问题
(1)求甲数是乙数的几(百)分之几。
甲数÷乙数=甲数是乙数的几(百)分之几
(2)已知甲数是乙数的几(百)分之几,求甲数。
乙数×几(百)分之几=甲数
(3)已知甲数是乙数的几(百)分之几,求乙数。
甲数÷几(百)分之几=乙数
分数或百分数问题
(4)求甲数比乙数多(少)几(百)分之几。
两个数的差÷乙数=
甲数比乙数多(少)的几(百)分之几
(5)已知甲数比乙数多(少)几(百)分之几,求甲数。
乙数×[1±几(百)分之几]=甲数
(6)已知甲数比乙数多(少)几(百)分之几,求乙数。
甲数÷[1±几(百)分之几]=乙数
折扣问题、成数问题、纳税问题、储蓄问题都可以转化为一般的百分数问题来分析解答。
折扣问题
成数问题
储蓄问题
纳税问题
现价÷折扣=原价
现价÷原价=折扣
几成就是十分之几,也就是百分之几十。
应纳税所得额×税率=应纳税额
利息=本金×利率×存期
原价×折扣=现价
行程问题
两个物体从两地出发,相向而行,经过一段时间后相遇。
两个物体同时不同地(或同地不同时或不同地不同时)出发,同向而行,后面的物体的速度快,在一定时间内能追上前面物体。
相遇问题
追及问题
题中每份的量保持不变,解题时先求出不变的单一量,再求出未知量。
主要是研究工作总量、工作时间和工作效率三者之间关系问题。
工作总量=工作效率×工作时间
解题时,通常把工作总量看成单位“1”。
归一问题
工程问题
此类题蕴含着“总量”不变,解题时,先求出总量,再求出未知量。
归总问题
已知大、小两个数的和与差,求这两个数分别是多少。
已知两个数的差及这两个数的倍数关系,求这两个数分别是多少。
和差问题
差倍问题
已知两个数的和及这两个数的倍数关系,求这两个数分别是多少。
和倍问题
王老师要买190本《数学小词典》,单价是3.80元/本。她带了800元钱,够吗?应找回(或再付)多少元?
根据解决问题的需要,怎样选择合理的计算方法?
从题中,你知道了哪些数学信息?
每本3.8元
要买190本
1.怎样选择合理的计算方法?
2.怎样解决“带了800元钱,够吗?”这个问题。
一
想
想
3. 8 0
× 1 9 0
3 4 2
3 8 0
7 2 2. 0 0
3.80 ×190
=722 (元)
722 <800
答:带800元钱够了。
笔算可以解决这个问题。
方法一
每本3.8元
要买190本
方法二
用简便方法口算解决这个问题。
3.80 ×190
= 722 (元)
722 <800
答:带800元钱够了。
3.80 × 190
= 3.80 × 200 - 3.80 × 10
= 760 - 38
= 722(元)
每本3.8元
要买190本
方法三
用计算器计算也可以解决这个问题。
722 < 800
答:带800元钱够了。
3.80 ×190
722 (元)
=
每本3.8元
要买190本
要解决的问题是“带了800元钱够吗?”,不需要求出精确的结果,求近似值即可,所以用估算就可以解决。
方法四
每本3.8元
要买190本
用估算可以解决这个问题。
3.80 ×190
答:带800元钱够了。
3.80 ≈ 4
4×200 = 800(元)
190 ≈ 200
≈800(元)
想一想,在选择计算方法解决问题的过程中,我们经历了怎样一个过程?
问题情境
王老师买词典
需要计算
带了800元钱,够吗?
应找回(或再付)多少元?
只需要近似值
需要精确值
估算
3.80≈4
190≈200
4×200=800
口算
3.80×200-3.80×10
笔算
3. 8 0
× 1 9 0
用计算器算
3.80×190
计算比较简单,能够快速解决问题
计算结果精确,但过程相对较为复杂。
计算过程简便、快捷,结果精确,但计算器携带不便。
如图,要为这样一个饮料罐的外壁制作标签纸,至少需要多少纸?
5×3.14×14
= 219.8(平方厘米)
这里用到了小数乘法计算。
“图形与几何”“统计与可能性”等知识的学习是不是也要用到计算?谈谈你的看法。
再如:六年级一周30节课,各学科课时占总课时的百分比如下图。一周有多少节语文课?
30×23.3%≈7(节)
计算在数学学习中非常重要,大部分的知识要用到计算。
这里用到了分数乘法计算。
课堂练习
1.小刚和小明分别从书店和学校同时出发去体育馆。小刚平均每分钟走60米。如果两人要同时到达,小明平均每分钟要走多少米
360÷60=6(分)
240÷6=40(米)
答:小明平均每分钟走40米。
360米
240米
教材第91页“应用与反思”第7题
“两人同时到达体育馆”表示两人走的时间是一样的,先根据“时间=路程(360)÷速度(60)”求出所需时间,再根据“速度=路程(240)÷时间”求出小明的速度。
2.一列火车从A城开往B城。如果速度是120千米/时,则4小时可以到达;如果速度是160千米/时,几小时可以到达
120×4÷160=3(时)
答:3小时可以到达。
教材第91页“应用与反思”第8题
先求出路程,路程是不变量,再根据“时间=路程÷速度”求出提速后所需的时间。
教材第91页“应用与反思”第9题
3.学校食堂计划购买1500千克大米。
(1)如果平均每天吃95千克,这些大米够吃半个月吗 (一个月按30天计算)
(2)如果够了,还剩下多少千克 如果不够,还需要购进多少千克
要解答“这些大米够不够吃半个月”的问题,需要估算还是精确计算
要解答“剩下多少千克”或“需要购进多少千克”的问题呢
3.学校食堂计划购买1500千克大米。
(1)如果平均每天吃95千克,这些大米够吃半个月吗 (一个月按30天计算)
这些大米
够吃半个
月吗?
只需要
近似值
估算:95≈100
100×15=1500(千克)
答:够了。
教材第91页“应用与反思”第9题
因为把95估成100时,数变大了,所以估算的积大于实际的积,也就是说实际半个月吃不了1500千克大米。因此,这些大米够吃半个月。
3.学校食堂计划购买1500千克大米。
(2)如果够了,还剩下多少千克 如果不够,还需要购进多少千克
教材第91页“应用与反思”第9题
还剩下(还
需要购进)
多少千克?
需要精
确计算
先求半个月需要多少千克大米:
95×(30÷2)=1425(千克)
再求还剩下多少千克:
1500-1425=75(千克)
答:还剩下75千克。
教材第91页“应用与反思”第10题
4.下面是王阿姨某天卖出报刊情况记录表。
(1)《都市晚报》和《京华晨报》一共卖了多少元
单件(元) 数量
《都市晚报》 0.50 90份
《京华晨报》 0.30 85份
《电脑世界》 1.85 25本
《城市生活》 5.70 9本
总价=单价×数量
(1)0.50×90+0.30×85=70.50(元)
答:一共卖了70.5元。
4.下面是王阿姨某天卖出报刊情况记录表。
单件(元) 数量
《都市晚报》 0.50 90份
《京华晨报》 0.30 85份
《电脑世界》 1.85 25本
《城市生活》 5.70 9本
(2) 《电脑世界》和《城市生活》哪种卖的钱多 多多少元
教材第91页“应用与反思”第10题
总价=单价×数量
(2)《电脑世界》:1.85×25=46.25(元)
《城市生活》:5.70×9=51.30(元) 46.25<51.30
51.30-46.25=5.05(元)
答:《城市生活》卖的钱多,比《电脑世界》多5.05元。
教材第92页“应用与反思”第11题
5.青山小学六年级有学生126人,报名参加冬季越野比赛的占,其中男生占。参加越野比赛的男生有多少人
答:参加越野比赛的男生有70人。
126××=70(人)
先求报名冬季越野比赛的学生有多少,用总人数乘;再求其中的男生有多少人,用上一步的结果乘,即可解决问题。
教材第92页“应用与反思”第12题
6.你知道动物的牙齿数吗 猫有30颗,马有36颗,兔有28颗,狗的牙齿数比猫的多,大象的牙齿数只相当于马的。
请根据上面的信息填表。
动物 猫 马 兔 狗 大象
牙齿数(颗)
30
36
28
42
6
猫的牙齿数×+猫的牙齿数
马的牙齿数×
教材第92页“应用与反思”第13题
7. (1)质监局对全市儿童服装产品进行质量抽检。在抽检的产品中有48个品牌产品合格,有2个品牌产品不合格。本次抽检的合格率是多少
48÷(48+2)×100%=96%
答:本次抽检的合格率是96%。
合格率=合格数÷总数
教材第92页“应用与反思”第13题
8. (2)大豆的出油率是18%。现有250千克大豆,能榨出50千克豆油吗
250×18%=45(千克)
45<50
答:250千克大豆不能榨出50千克豆油。
榨出的油的质量=大豆的质量×出油率
教材第92页“应用与反思”第14题
9.一种“感冒通”片的两种主要药物成分是人工牛黄( 12%)和马来酸氯苯那敏( 2%)。制药厂要配制5000克这样的“感冒通”片,这两种药物分别需要多少克
解决上面的问题需要精确计算吗
需要
人工牛黄:5000×12%=600(克)
马来酸氯苯那敏:5000×2%=100(克)
教材第93页“应用与反思”第16题
10. 大连、烟台两个港口相距87海里。 甲、乙两船分别从两个港口同时出发,相向而行,3小时后相遇。乙船每小时行15海里,甲船每小时行多少海里
87÷3-15=14(海里)
答:甲船每小时行驶14海里。
所求问题是“甲船每小时行多少海里?”,需要求出确切的速度,所以要精确计算。
速度和=路程÷相遇时间
教材第93页“应用与反思”第17题
11.
(1) 2017年1月9日,王平的爸爸在银行存了20000元钱,定期一年,年利率是1.75%。 到期后应得利息多少元
20000×1.75%×1=350(元)
答:到期后应得利息350元。
利息=本金×利率×存期
教材第93页“应用与反思”第17题
(2)一种上衣原价为120元,现按七折销售,便宜了多少元
120-120×70%=36(元)
答:便宜了36元。
几折就是十分之几,也就是百分之几十。
原价×折扣=现价
教材第93页“应用与反思”第17题
(3)商场12月份销售的女装数量比男装多25%,男装销售了1280件,女装销售了多少件
1280×(1+25%)=1600(件)
答:女装销售了1600件。
男装销售件数×25%=女装比男装多销售的件数
女装销售件数=男装销售件数+女装比男装多销售的件数
教材第93页“应用与反思”第18题
12. 李大爷家养的鸡、鸭、鹅共3000只。
3000×30%-3000×18%=360(只)
答:鸭比鹅多360只。
鸭比鹅多多少只
教材第93页“应用与反思”第19题
13.河东区要修一条640米的景观大道,第一周修了这条路的第二周修了这条路的20%,还剩多少米没修
640-640× - 640×20%=352(米)
答:还剩下352米没有修。
教材第93页“应用与反思”第20题
14.下表是A、B、C三个城市绿化面积的有关信息。
城市 A B C
总面积(万平方千米) 0.7 1.1 1.5
绿化面积(万平方千米) 0.23 0.25 0.27
哪个城市的绿化情况好一些?
直接比较绿化面积能反映三个城市的绿化情况吗
应该比较它们的绿化率.....
教材第93页“应用与反思”第20题
因为A、B、C三个城市的总面积不同,所以直接比较绿化面积不能反映三个城市的绿化情况,应该比较它们的绿化率。
答:A城市的绿化情况好一些。
32.9%>22.7%>18%
A城市:0.23÷0.7×100%≈32.9%
B城市:0.25÷1.1×100%≈22.7%
C城市:0.27÷1.5×100%≈18%
教材第93页“应用与反思”第21题
15.超市有鸡蛋40箱、鸭蛋30箱,共重275千克。已知1箱鸡蛋的质量和2箱鸭蛋的质量相等,1箱鸡蛋的质量是多少千克
1箱鸭蛋的质量:275÷(40×2+30)=2.5(千克)
1箱鸡蛋的质量:2.5×2=5(千克)
答:一箱鸡蛋的质量是5千克。
假设全部是鸭蛋,则鸭蛋共有( 40×2+30 )箱,根据 “总质量÷箱数=1箱的质量”先求出1箱鸭蛋的质量。
思路一
教材第93页“应用与反思”第21题
15.超市有鸡蛋40箱、鸭蛋30箱,共重275千克。已知1箱鸡蛋的质量和2箱鸭蛋的质量相等,1箱鸡蛋的质量是多少千克
1箱鸡蛋的质量:275÷(40+30÷2)=5(千克)
答:一箱鸡蛋的质量是5千克。
假设全部是鸡蛋,则鸡蛋共有( 40+30÷2 )箱,根据 “总质量÷箱数=1箱的质量”求出1箱鸡蛋的质量。
思路二
相关练习。
02
01
课后练习题。
课后作业
