23.2解直角三角形应用 2021-2022学年沪科版数学九年级上册(word版含答案)
文档属性
| 名称 | 23.2解直角三角形应用 2021-2022学年沪科版数学九年级上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 646.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 14:51:54 | ||
图片预览



文档简介
解直角三角形应用
一.选择题
如图,从点看一山坡上的电线杆,观测点的仰角是,向前走到达点,测得顶端点和杆底端点的仰角分别是和,则该电线杆的高度
B.
C. D.
某次台风来袭时,一棵大树树干假定树干垂直于地面被刮倾斜后折断倒在地上,树的项部恰好接触到地面如图所示,量得树干的倾斜角为,大树被折断部分和地面所成的角,米,求这棵大树原来的高度是米?结果精确到个位,参考数据:,,
B. C. D.
如图,在矩形中,点在上,将矩形沿折叠,使点落在边上的点处.若,,则的值为
B. C. D.
如图,在距某居民楼楼底点左侧水平距离的点处有一个山坡,山坡的坡度或坡比:,山坡坡底点到坡顶点的距离,在坡顶点处测得居民楼楼顶点的仰角为,居民楼与山坡的剖面在同一平面内,则居民楼的高度约为参考数据:,,
B. C. D.
二.填空题
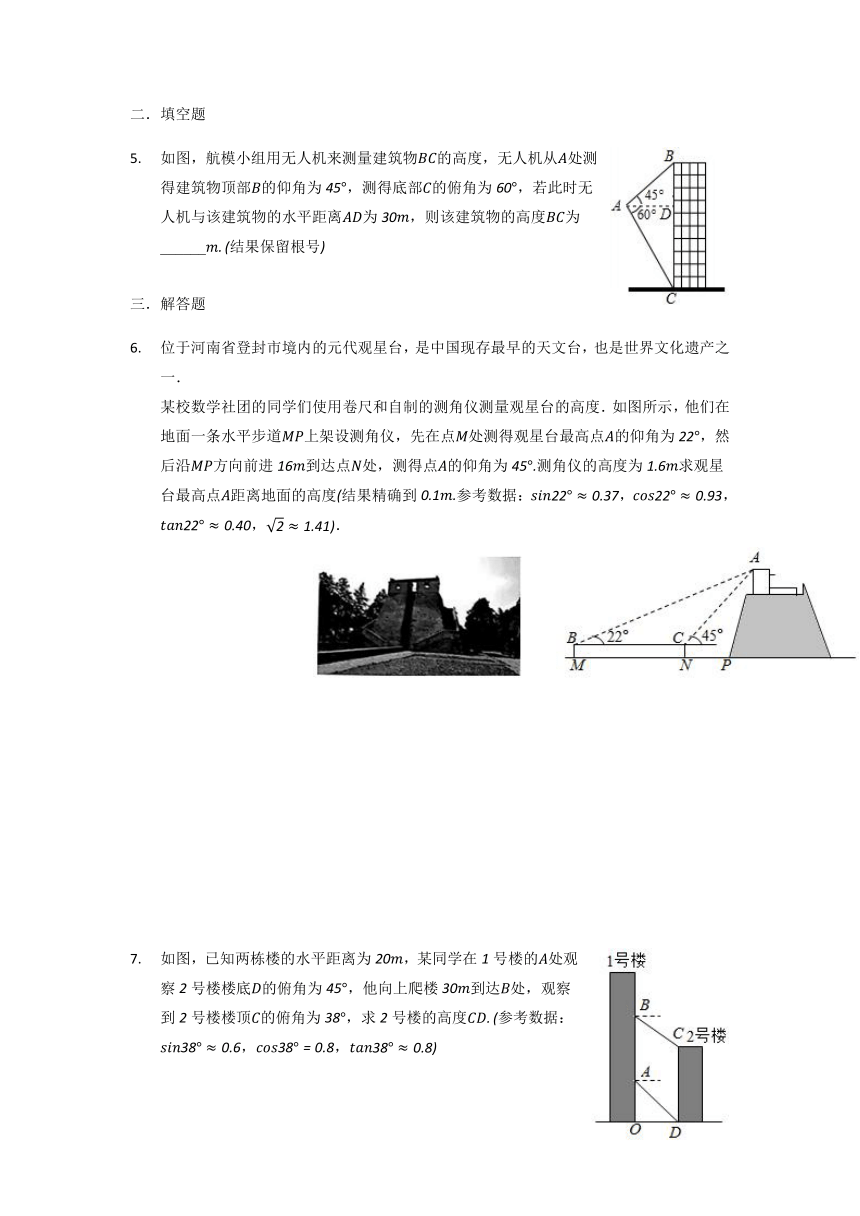
如图,航模小组用无人机来测量建筑物的高度,无人机从处测得建筑物顶部的仰角为,测得底部的俯角为,若此时无人机与该建筑物的水平距离为,则该建筑物的高度为______结果保留根号
三.解答题
位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道上架设测角仪,先在点处测得观星台最高点的仰角为,然后沿方向前进到达点处,测得点的仰角为测角仪的高度为求观星台最高点距离地面的高度结果精确到参考数据:,,,.
如图,已知两栋楼的水平距离为,某同学在号楼的处观察号楼楼底的俯角为,他向上爬楼到达处,观察到号楼楼顶的俯角为,求号楼的高度参考数据:,,
安徽滁州琅琊山会峰阁更名为琅琊阁,如图是悬挂着巨大匾额的琅琊阁,如图,线段是悬挂在墙壁上的匾额的截面示意图.已知米,,从水平地面点处看点,仰角,从点处看点,仰角,且米,求匾额悬挂的高度的长.结果精确到米,参考数据:,,
在“停课不停学”期间,小明用电脑在线上课,图是他的电脑液晶显示器的侧面图,显示屏可以绕点旋转一定角度.研究表明:当眼睛与显示屏顶端在同一水平线上,且望向显示器屏幕形成一个俯角即望向屏幕中心的的视线与水平线的夹角时,对保护眼睛比较好,而且显示屏顶端与底座的连线与水平线垂直时如图时,观看屏幕最舒适,此时测得,,液晶显示屏的宽为.
求眼睛与显示屏顶端的水平距离;结果精确到
求显示屏顶端与底座的距离结果精确到
参考数据:,,,,
如图,在 中,,交于点,且.
求证:四边形是矩形;
的角平分线交于点,当,时,求的长.
如图,山顶有一塔,塔高计划在塔的正下方沿直线开通穿山隧道从与点相距的处测得、的仰角分别为、,从与点相距的处测得的仰角为求隧道的长度.
参考数据:,
如图,是某小区的甲、乙两栋住宅楼,小丽站在甲栋楼房的楼顶,测量对面的乙栋楼房的高度.已知甲栋楼房与乙栋楼房的水平距离米,小丽在甲栋楼房顶部点,测得乙栋楼房顶部点的仰角是,底部点的俯角是,求乙栋楼房的高度结果保留根号.
某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度,他们先在点用高米的测角仪测得塔顶的仰角为,然后沿方向前行到达点处,在处测得塔顶的仰角为请根据他们的测量数据求此塔的高.结果精确到,参考数据:,,
数学兴趣小组到黄河风景名胜区测量炎帝塑像塑像中高者的高度.如图所示,炎帝塑像在高的小山上,在处测得塑像底部的仰角为,再沿方向前进到达处,测得塑像顶部的仰角为,求炎帝塑像的高度.精确到参考数据:,,,
如图,两座建筑物的水平距离为,从点测得点的俯角为,测得点的俯角为求这两座建筑物,的高度.结果保留小数点后一位,,
自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图所示的坡路进行改造.如图所示,改造前的斜坡米,坡度为:;将斜坡的高度降低米后,斜坡改造为斜坡,其坡度为:求斜坡的长.结果保留根号
如图,一艘船由港沿北偏东方向航行至港,然后再沿北偏西方向航行至港,港在港北偏东方向,
求的度数.
,两港之间的距离为多少.
如图,我国某海域有,两个港口,相距海里,港口在港口的东北方向,点处有一艘货船,该货船在港口的北偏西方向,在港口的北偏西方向,求货船与港口之间的距离.结果保留根号
如图是自动卸货汽车卸货时的状态图,图是其示意图.汽车的车厢采用液压机构、车厢的支撑顶杆的底部支撑点在水平线的下方,与水平线之间的夹角是,卸货时,车厢与水平线成,此时与支撑顶杆的夹角为,若米,求的长度.结果保留一位小数
参考数据:,,,,,,
如图,在南北方向的海岸线上,有,两艘巡逻船,现均收到故障船的求救信号.已知,两船相距海里,船在船的北偏东方向上,船在船的东南方向上,上有一观测点,测得船正好在观测点的南偏东方向上.
分别求出与,与间的距离和如果运算结果有根号,请保留根号.
已知距观测点处海里范围内有暗礁,若巡逻船沿直线去营救船,在去营救的途中有无触礁的危险?参考数据:,
如图是某路灯在铅垂面内的示意图,灯柱的高为米,灯杆与灯柱的夹角,路灯采用锥形灯罩,在地面上的照射区域长为米,从,两处测得路灯的仰角分别为和,且,,求灯杆的长度.
一艘轮船位于灯塔南偏西方向的处,它向东航行海里到达灯塔南偏西方向上的处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔的最短距离.结果保留根号
如图,某人为了测量小山顶上的塔的高,他在山下的点处测得塔尖点的仰角为,再沿方向前进到达山脚点,测得塔尖点的仰角为,塔底点的仰角为,求塔的高度.结果保留根号
为加快城乡对接,建设全域美丽乡村,某地区对、两地间的公路进行改建.如图,、两地之间有一座山,汽车原来从地到地需途经地沿折线行驶,现开通隧道后,汽车可直接沿直线行驶.已知千米,,.
开通隧道前,汽车从地到地大约要走多少千米?
开通隧道后,汽车从地到地大约可以少走多少千米?结果精确到千米参考数据:,
风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成如图,图是从图引出的平面图.假设你站在处测得塔杆顶端的仰角是,沿方向水平前进米到达山底处,在山顶处发现正好一叶片到达最高位置,此时测得叶片的顶端、、在同一直线上的仰角是已知叶片的长度为米塔杆与叶片连接处的长度忽略不计,山高为米,,,求塔杆的高.参考数据:,,,
脱贫攻坚工作让老百姓过上了幸福的生活.如图是政府给贫困户新建的房屋,如图是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线,为了测量房屋的高度,在地面上点测得屋顶的仰角为,此时地面上点、屋檐上点、屋顶上点三点恰好共线,继续向房屋方向走到达点时,又测得屋檐点的仰角为,房屋的顶层横梁,,交于点点,,在同一水平线上参考数据:,,,
求屋顶到横梁的距离;
求房屋的高结果精确到.
答案
1.【答案】
【解析】解:延长交直线于点,设米.
在直角中,,
则米;
在直角中,米,
米,
则,
解得:.
则米.
在直角中,米.
米.
答:电线杆的高度是米.
故选:.
2.【答案】
解:过点作于点,
,
,
,
在中,
,
,
,
,
,
在中,
,
,
,
,
,
米.
答:这棵大树原来的高度是米.
故选:.
3.【答案】
【解析】解:四边形为矩形,
,,
矩形沿直线折叠,顶点恰好落在边上的处,
,,
在中,,
,
设,则
在中,,
,解得,
,
,
故选:.
4.【答案】
【解析】解:如图,由题意得,,,,
在中,
山坡的坡度:,
,
设,则,由勾股定理可得,
又,即,
,
,,
,
在中,
,
,
故选:.
5.【解析】解:在中,,,
,
在中,,
,
答:该建筑物的高度约为米.
故答案为:.
6.【答案】解:过作于,延长交于,
则四边形,四边形是矩形,
,,
,,
是等腰直角三角形,
,
设,
,
,
,
解得:,
,
答:观星台最高点距离地面的高度约为.
7.【答案】解:如图,过点作于点,得矩形,
,,
根据题意可知:
,,
,
,
,
,
在中,,
,
,
解得,
答:号楼的高度为.
8.【答案】解:过点作,,垂足为、,如图所示:
在中,
米,
米,
在中,
,
,
,
,
即:,
解得,米
答:匾额悬挂的高度的长约为米.
9.【答案】解:由已知得,
在中,
,
,
答:眼睛与显示屏顶端的水平距离约为;
如图,过点作于点,
,,
,
在中,
,
,
,
,
,
.
答:显示屏顶端与底座的距离约为.
10.【答案】证明:四边形是平行四边形,
,.
,
.
为矩形.
解:过点作于点,如图所示:
四边形是矩形,
,
,
为的角平分线,
.
,
.
,,
.
.
,.
设,则,
在中,,
.
解得:,
.
11.【答案】解:延长交于,
则,
在中,,
,
在中,,
,
在中,,
,
由题意得,,
解得,,
,,
,
,
,
,
答:隧道的长度为.
12.【答案】解:如图所示:
由题意得:,,,,
在中,,,
,
在中,,
是等腰直角三角形,
,
米;
答:乙栋楼房的高度为米.
13.【答案】解:由题意:,,,,
,,
,
在中,
,,
.
,
,
,
.
14.【答案】解:,,,
,
,
,
,
在中,,
则,
,
,
答:炎帝塑像的高度约为.
15.【答案】解:延长,交于点,可得,
在中,,,
,
在中,,,
,
则.
答:这两座建筑物、的高度分别为和.
16.【答案】解:,,坡度为:,
,
,
,
,
,
,斜坡的坡度为:,
,
即,
解得,,
米,
答:斜坡的长是米.
17.【答案】解:由题意得:;
由题意得,,,,
过作于,如图所示:
,
在中,,
是等腰直角三角形,
,
,
在中,,,
,
,
,两港之间的距离为.
18.【答案】解:过点作于,如图所示:
由题意得:,
,
,
在中,,,
,,
,
,
是等腰直角三角形,
海里.
答:货船与港口之间的距离是海里.
19.【答案】解:如图,过点作于点,
在中,,
米,
在中,,
,
米,
答:所求的长度约为米.
20.【答案】解:如图,作于,
由题意得:,,
设海里,
在中,;
在中,
,
解得:.
.
在中,,,则.
过点作于点,
设,则,
,
解得:,
.
答:与之间的距离为海里,与之间的距离为海里.
由可知,海里,
因为,
所以巡逻船沿直线航线,在去营救的途中没有触暗礁危险.
21.【答案】解:过点作,交于点,过点作,交于点,则.
由题意得,.
设,则
在中,,
,
,
.
.
,
,
,
.
,
答:灯杆的长度为米.
22.【答案】解:如图,,,,海里,设海里,则海里.
在中,,
为等腰直角三角形,
海里,
在中,,
,
,
解得,
则海里.
答:轮船航行途中与灯塔的最短距离是海里.
23.【答案】解:由题知,,,
.
又,
.
.
.
设,则,,
,
由题知,,,,
为等腰直角三角形,
.
,
解得:,
.
答:塔高约为.
24.【答案】解:过点作的垂线,垂足为,
,,千米,
千米,
千米,
千米,
答:开通隧道前,汽车从地到地要走千米;
,千米,
千米,
,千米,
千米,
千米,
汽车从地到地比原来少走多少路程为:千米.
答:汽车从地到地比原来少走的路程为千米.
25.【答案】解:如图,作于点,
则、,
设,则,
在中,,
,
,
,即,
解得:,
,
答:塔杆的高为米.
26.【答案】解:房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线,,
,,,
在中,,,
,,
米;
答:屋顶到横梁的距离为米;
过作于,
设,
在中,,,
,
,
在中,,,
,
,
,
,
解得:,
米,
答:房屋的高为米.
一.选择题
如图,从点看一山坡上的电线杆,观测点的仰角是,向前走到达点,测得顶端点和杆底端点的仰角分别是和,则该电线杆的高度
B.
C. D.
某次台风来袭时,一棵大树树干假定树干垂直于地面被刮倾斜后折断倒在地上,树的项部恰好接触到地面如图所示,量得树干的倾斜角为,大树被折断部分和地面所成的角,米,求这棵大树原来的高度是米?结果精确到个位,参考数据:,,
B. C. D.
如图,在矩形中,点在上,将矩形沿折叠,使点落在边上的点处.若,,则的值为
B. C. D.
如图,在距某居民楼楼底点左侧水平距离的点处有一个山坡,山坡的坡度或坡比:,山坡坡底点到坡顶点的距离,在坡顶点处测得居民楼楼顶点的仰角为,居民楼与山坡的剖面在同一平面内,则居民楼的高度约为参考数据:,,
B. C. D.
二.填空题
如图,航模小组用无人机来测量建筑物的高度,无人机从处测得建筑物顶部的仰角为,测得底部的俯角为,若此时无人机与该建筑物的水平距离为,则该建筑物的高度为______结果保留根号
三.解答题
位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道上架设测角仪,先在点处测得观星台最高点的仰角为,然后沿方向前进到达点处,测得点的仰角为测角仪的高度为求观星台最高点距离地面的高度结果精确到参考数据:,,,.
如图,已知两栋楼的水平距离为,某同学在号楼的处观察号楼楼底的俯角为,他向上爬楼到达处,观察到号楼楼顶的俯角为,求号楼的高度参考数据:,,
安徽滁州琅琊山会峰阁更名为琅琊阁,如图是悬挂着巨大匾额的琅琊阁,如图,线段是悬挂在墙壁上的匾额的截面示意图.已知米,,从水平地面点处看点,仰角,从点处看点,仰角,且米,求匾额悬挂的高度的长.结果精确到米,参考数据:,,
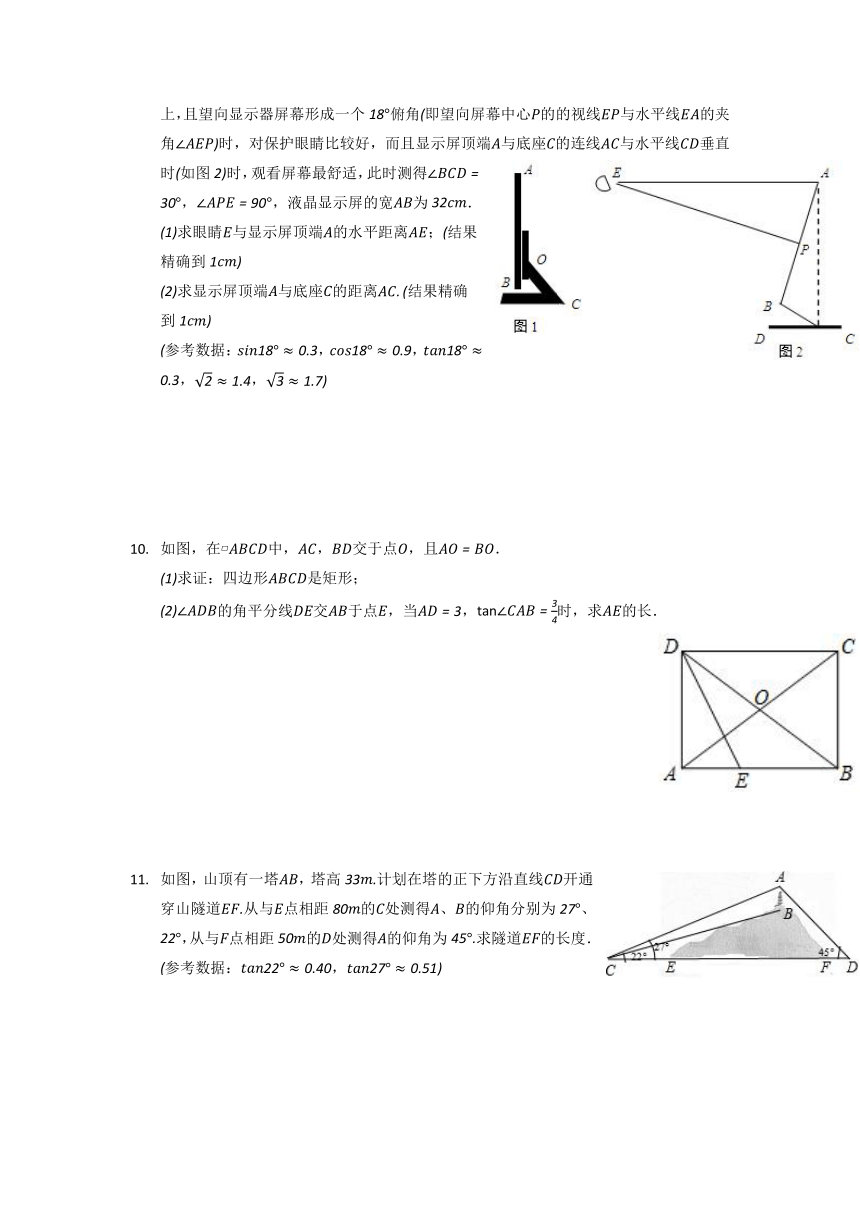
在“停课不停学”期间,小明用电脑在线上课,图是他的电脑液晶显示器的侧面图,显示屏可以绕点旋转一定角度.研究表明:当眼睛与显示屏顶端在同一水平线上,且望向显示器屏幕形成一个俯角即望向屏幕中心的的视线与水平线的夹角时,对保护眼睛比较好,而且显示屏顶端与底座的连线与水平线垂直时如图时,观看屏幕最舒适,此时测得,,液晶显示屏的宽为.
求眼睛与显示屏顶端的水平距离;结果精确到
求显示屏顶端与底座的距离结果精确到
参考数据:,,,,
如图,在 中,,交于点,且.
求证:四边形是矩形;
的角平分线交于点,当,时,求的长.
如图,山顶有一塔,塔高计划在塔的正下方沿直线开通穿山隧道从与点相距的处测得、的仰角分别为、,从与点相距的处测得的仰角为求隧道的长度.
参考数据:,
如图,是某小区的甲、乙两栋住宅楼,小丽站在甲栋楼房的楼顶,测量对面的乙栋楼房的高度.已知甲栋楼房与乙栋楼房的水平距离米,小丽在甲栋楼房顶部点,测得乙栋楼房顶部点的仰角是,底部点的俯角是,求乙栋楼房的高度结果保留根号.
某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度,他们先在点用高米的测角仪测得塔顶的仰角为,然后沿方向前行到达点处,在处测得塔顶的仰角为请根据他们的测量数据求此塔的高.结果精确到,参考数据:,,
数学兴趣小组到黄河风景名胜区测量炎帝塑像塑像中高者的高度.如图所示,炎帝塑像在高的小山上,在处测得塑像底部的仰角为,再沿方向前进到达处,测得塑像顶部的仰角为,求炎帝塑像的高度.精确到参考数据:,,,
如图,两座建筑物的水平距离为,从点测得点的俯角为,测得点的俯角为求这两座建筑物,的高度.结果保留小数点后一位,,
自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图所示的坡路进行改造.如图所示,改造前的斜坡米,坡度为:;将斜坡的高度降低米后,斜坡改造为斜坡,其坡度为:求斜坡的长.结果保留根号
如图,一艘船由港沿北偏东方向航行至港,然后再沿北偏西方向航行至港,港在港北偏东方向,
求的度数.
,两港之间的距离为多少.
如图,我国某海域有,两个港口,相距海里,港口在港口的东北方向,点处有一艘货船,该货船在港口的北偏西方向,在港口的北偏西方向,求货船与港口之间的距离.结果保留根号
如图是自动卸货汽车卸货时的状态图,图是其示意图.汽车的车厢采用液压机构、车厢的支撑顶杆的底部支撑点在水平线的下方,与水平线之间的夹角是,卸货时,车厢与水平线成,此时与支撑顶杆的夹角为,若米,求的长度.结果保留一位小数
参考数据:,,,,,,
如图,在南北方向的海岸线上,有,两艘巡逻船,现均收到故障船的求救信号.已知,两船相距海里,船在船的北偏东方向上,船在船的东南方向上,上有一观测点,测得船正好在观测点的南偏东方向上.
分别求出与,与间的距离和如果运算结果有根号,请保留根号.
已知距观测点处海里范围内有暗礁,若巡逻船沿直线去营救船,在去营救的途中有无触礁的危险?参考数据:,
如图是某路灯在铅垂面内的示意图,灯柱的高为米,灯杆与灯柱的夹角,路灯采用锥形灯罩,在地面上的照射区域长为米,从,两处测得路灯的仰角分别为和,且,,求灯杆的长度.
一艘轮船位于灯塔南偏西方向的处,它向东航行海里到达灯塔南偏西方向上的处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔的最短距离.结果保留根号
如图,某人为了测量小山顶上的塔的高,他在山下的点处测得塔尖点的仰角为,再沿方向前进到达山脚点,测得塔尖点的仰角为,塔底点的仰角为,求塔的高度.结果保留根号
为加快城乡对接,建设全域美丽乡村,某地区对、两地间的公路进行改建.如图,、两地之间有一座山,汽车原来从地到地需途经地沿折线行驶,现开通隧道后,汽车可直接沿直线行驶.已知千米,,.
开通隧道前,汽车从地到地大约要走多少千米?
开通隧道后,汽车从地到地大约可以少走多少千米?结果精确到千米参考数据:,
风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成如图,图是从图引出的平面图.假设你站在处测得塔杆顶端的仰角是,沿方向水平前进米到达山底处,在山顶处发现正好一叶片到达最高位置,此时测得叶片的顶端、、在同一直线上的仰角是已知叶片的长度为米塔杆与叶片连接处的长度忽略不计,山高为米,,,求塔杆的高.参考数据:,,,
脱贫攻坚工作让老百姓过上了幸福的生活.如图是政府给贫困户新建的房屋,如图是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线,为了测量房屋的高度,在地面上点测得屋顶的仰角为,此时地面上点、屋檐上点、屋顶上点三点恰好共线,继续向房屋方向走到达点时,又测得屋檐点的仰角为,房屋的顶层横梁,,交于点点,,在同一水平线上参考数据:,,,
求屋顶到横梁的距离;
求房屋的高结果精确到.
答案
1.【答案】
【解析】解:延长交直线于点,设米.
在直角中,,
则米;
在直角中,米,
米,
则,
解得:.
则米.
在直角中,米.
米.
答:电线杆的高度是米.
故选:.
2.【答案】
解:过点作于点,
,
,
,
在中,
,
,
,
,
,
在中,
,
,
,
,
,
米.
答:这棵大树原来的高度是米.
故选:.
3.【答案】
【解析】解:四边形为矩形,
,,
矩形沿直线折叠,顶点恰好落在边上的处,
,,
在中,,
,
设,则
在中,,
,解得,
,
,
故选:.
4.【答案】
【解析】解:如图,由题意得,,,,
在中,
山坡的坡度:,
,
设,则,由勾股定理可得,
又,即,
,
,,
,
在中,
,
,
故选:.
5.【解析】解:在中,,,
,
在中,,
,
答:该建筑物的高度约为米.
故答案为:.
6.【答案】解:过作于,延长交于,
则四边形,四边形是矩形,
,,
,,
是等腰直角三角形,
,
设,
,
,
,
解得:,
,
答:观星台最高点距离地面的高度约为.
7.【答案】解:如图,过点作于点,得矩形,
,,
根据题意可知:
,,
,
,
,
,
在中,,
,
,
解得,
答:号楼的高度为.
8.【答案】解:过点作,,垂足为、,如图所示:
在中,
米,
米,
在中,
,
,
,
,
即:,
解得,米
答:匾额悬挂的高度的长约为米.
9.【答案】解:由已知得,
在中,
,
,
答:眼睛与显示屏顶端的水平距离约为;
如图,过点作于点,
,,
,
在中,
,
,
,
,
,
.
答:显示屏顶端与底座的距离约为.
10.【答案】证明:四边形是平行四边形,
,.
,
.
为矩形.
解:过点作于点,如图所示:
四边形是矩形,
,
,
为的角平分线,
.
,
.
,,
.
.
,.
设,则,
在中,,
.
解得:,
.
11.【答案】解:延长交于,
则,
在中,,
,
在中,,
,
在中,,
,
由题意得,,
解得,,
,,
,
,
,
,
答:隧道的长度为.
12.【答案】解:如图所示:
由题意得:,,,,
在中,,,
,
在中,,
是等腰直角三角形,
,
米;
答:乙栋楼房的高度为米.
13.【答案】解:由题意:,,,,
,,
,
在中,
,,
.
,
,
,
.
14.【答案】解:,,,
,
,
,
,
在中,,
则,
,
,
答:炎帝塑像的高度约为.
15.【答案】解:延长,交于点,可得,
在中,,,
,
在中,,,
,
则.
答:这两座建筑物、的高度分别为和.
16.【答案】解:,,坡度为:,
,
,
,
,
,
,斜坡的坡度为:,
,
即,
解得,,
米,
答:斜坡的长是米.
17.【答案】解:由题意得:;
由题意得,,,,
过作于,如图所示:
,
在中,,
是等腰直角三角形,
,
,
在中,,,
,
,
,两港之间的距离为.
18.【答案】解:过点作于,如图所示:
由题意得:,
,
,
在中,,,
,,
,
,
是等腰直角三角形,
海里.
答:货船与港口之间的距离是海里.
19.【答案】解:如图,过点作于点,
在中,,
米,
在中,,
,
米,
答:所求的长度约为米.
20.【答案】解:如图,作于,
由题意得:,,
设海里,
在中,;
在中,
,
解得:.
.
在中,,,则.
过点作于点,
设,则,
,
解得:,
.
答:与之间的距离为海里,与之间的距离为海里.
由可知,海里,
因为,
所以巡逻船沿直线航线,在去营救的途中没有触暗礁危险.
21.【答案】解:过点作,交于点,过点作,交于点,则.
由题意得,.
设,则
在中,,
,
,
.
.
,
,
,
.
,
答:灯杆的长度为米.
22.【答案】解:如图,,,,海里,设海里,则海里.
在中,,
为等腰直角三角形,
海里,
在中,,
,
,
解得,
则海里.
答:轮船航行途中与灯塔的最短距离是海里.
23.【答案】解:由题知,,,
.
又,
.
.
.
设,则,,
,
由题知,,,,
为等腰直角三角形,
.
,
解得:,
.
答:塔高约为.
24.【答案】解:过点作的垂线,垂足为,
,,千米,
千米,
千米,
千米,
答:开通隧道前,汽车从地到地要走千米;
,千米,
千米,
,千米,
千米,
千米,
汽车从地到地比原来少走多少路程为:千米.
答:汽车从地到地比原来少走的路程为千米.
25.【答案】解:如图,作于点,
则、,
设,则,
在中,,
,
,
,即,
解得:,
,
答:塔杆的高为米.
26.【答案】解:房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线,,
,,,
在中,,,
,,
米;
答:屋顶到横梁的距离为米;
过作于,
设,
在中,,,
,
,
在中,,,
,
,
,
,
解得:,
米,
答:房屋的高为米.
