第七章三角函数章节检测 -2021-2022学年高一数学人教B版(2019)必修第三册(含答案)
文档属性
| 名称 | 第七章三角函数章节检测 -2021-2022学年高一数学人教B版(2019)必修第三册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 853.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 11:43:49 | ||
图片预览



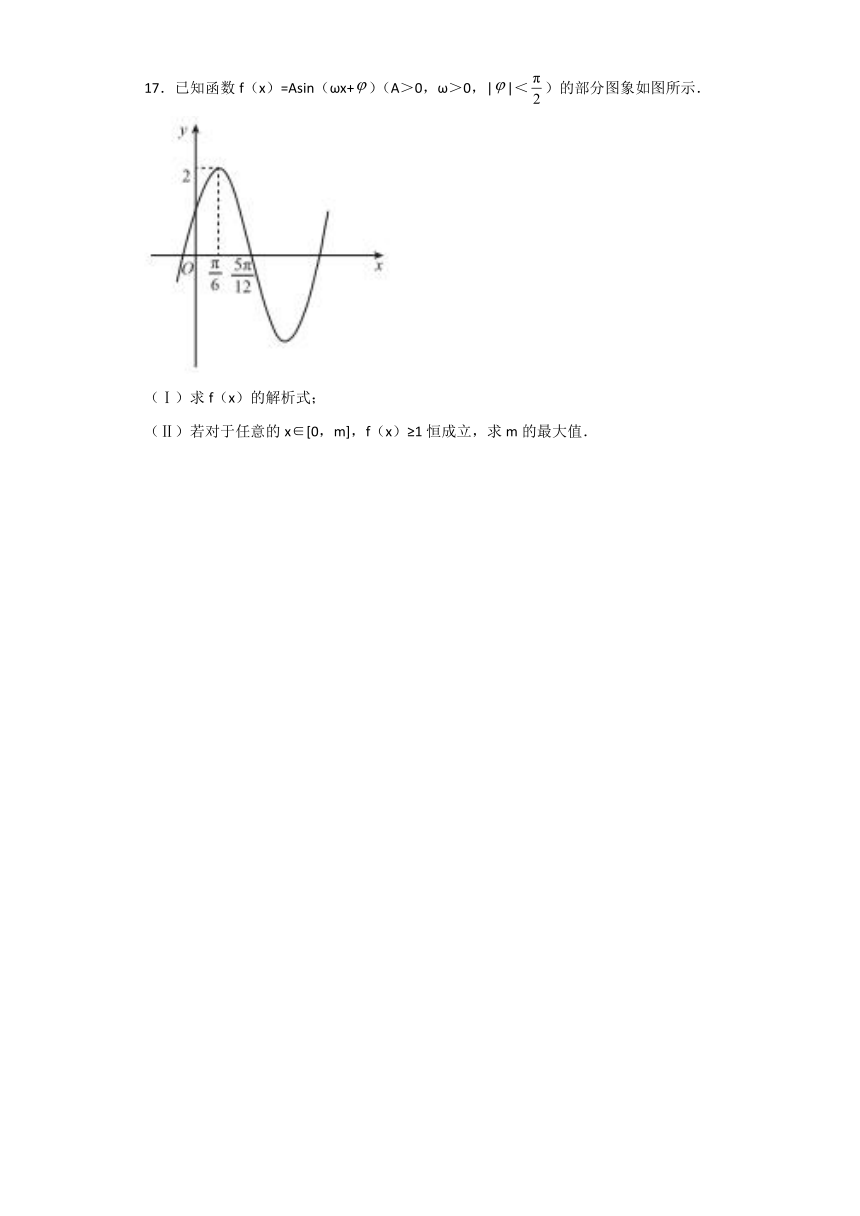
文档简介
北京·高一·同步练习
三角函数·章节检测
一、选择题(共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项)
1.下列各角中,与角终边相同的是( )
A. B. C. D.
2.已知,那么
A. B. C. D.
3.若,,则是( )
A.第四象限角 B.第三象限角 C.第二象限角 D.第一象限角
4.《九章算术》成书于公元一世纪,是中国古代乃至东方的第一部自成体系的数学专著.书中记载这样一个问题“今有宛田,下周三十步,径十六步.问为田几何?”(一步=1.5米)意思是现有扇形田,弧长为45米,直径为24米,那么扇形田的面积为
A.135平方米 B.270平方米 C.540平方米 D.1080平方米
5.若是的一个内角,且,则的值为
A. B. C. D.
6.将函数的图象上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是
A. B.
C. D.
7.集合M={Z},N={Z},则
A.MN B.NM C.MN= D.MN=R
8.函数的部分图象如图所示,为了得到的图象,只需将函数的图象
A.向左平移个单位长度 B.向左平移个单位长度
C.向右平移个单位长度 D.向右平移个单位长度
9.已知函数的一部分图象如图所示,如果,,,则( )
A. B. C. D.
10.将函数图象上所有点的横坐标缩短为原来的,纵坐标不变,再向右平移个单位长度,得到函数的图象,则下列说法正确的是
A.函数的一条对称轴是
B.函数的一个对称中心是
C.函数的一条对称轴是
D.函数的一个对称中心是
二、填空题(共5小题,每小题5分,共25分)
11.已知,则______.
12.已知角的始边与轴的非负半轴重合,顶点与坐标原点重合,终边过点,则____.
13.已知函数的图象如图所示,则该函数的解析式是__________.
14.已知函数,其中,是这两个函数图像的交点,且不共线.①当时,面积的最小值为___________;②若存在是等腰直角三角形,则的最小值为__________.
15.某地区每年各个月份的月平均最高气温近似地满足周期性规律,因此第个月的月平均最高气温可近似地用函数来刻画,其中正整数表示月份且,例如表示1月份,和是正整数,,.统计发现,该地区每年各个月份的月平均最高气温有以下规律:
①该地区月平均最高气温最高的7月份与最低的1月份相差30摄氏度;
②1月份该地区月平均最高气温为3摄氏度,随后逐月递增直到7月份达到最高;
③每年相同的月份,该地区月平均最高气温基本相同.
根据已知信息,得到的表达式是______.
三、解答题(共6小题,共85分。解答应写出文字说明、演算步骤或证明过程)
16.函数.
(1)求函数的单调递增区间和最小正周期;
(2)请用“五点法”画出函数在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
0
(3)求函数在上的最大值和最小值,并指出相应的的值.
17.已知函数f(x)=Asin(ωx+)(A>0,ω>0,||<)的部分图象如图所示.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若对于任意的x∈[0,m],f(x)≥1恒成立,求m的最大值.
18.某同学用“五点法”画函数在某一个周期内的图象时,列表并填入了部分数据,如下表:
0
0
5
0
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数的解析式;
(Ⅱ)将图象上所有点向左平行移动个单位长度,得到的图象.若图象的一个对称中心为,求的最小值.
19.如图所示,某地一天从6时至14时的温度变化曲线近似满足函数,其中,且函数在6时与14时分别取得最小值(最低温度)和最大值(最高温度).
(1)求这段时间的最大温差;
(2)写出这段曲线的函数解析式.
20.现给出三个条件:①函数的图象关于直线对称;②函数的图象关于点对称;③函数的图象上相邻两个最高点的距离为.从中选出两个条件补充在下面的问题中,并以此为依据求解问题.
已知函数(,),_____,_____.求函数在区间上的最大值和最小值.
21.已知函数,且图象的相邻两条对称轴之间的距离为,再从条件①、条件②、条件③中选择两个作为一组已知条件.
(1)确定的解析式;
(2)若图象的对称轴只有一条落在区间上,求a的取值范围.
条件①:的最小值为;
条件②:图象的一个对称中心为;
条件③;的图象经过点.
试卷第4页,共5页
参考答案
1.D
【分析】
写出与终边相同角的集合,取k值得答案.
【详解】
与角终边相同的角的集合为,
取,可得.
∴与角终边相同的是.
故选:D
【点睛】
本小题主要考查终边相同的角,属于基础题.
2.C
【分析】
试题分析:由,得 .故选C.
考点:诱导公式.
3.B
【分析】
根据三角函数的符号,确定终边上的点所处的象限,从而得到结果.
【详解】
则对应第三象限的点,即是第三象限角
本题正确选项:
【点睛】
本题考查各象限内三角函数值的符号,属于基础题.
4.B
【分析】
直接利用扇形面积计算得到答案.
【详解】
根据扇形的面积公式,计算扇形田的面积为Slr45270(平方米).
故选:B.
【点睛】
本题考查了扇形面积,属于简单题.
5.D
【详解】
试题分析:是的一个内角,,又,所以有,故本题的正确选项为D.
考点:三角函数诱导公式的运用.
6.C
【详解】
将函数的图象上所有的点向右平行移动个单位长度,所得函数图象的解析式为y=sin(x-);
再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是.故选C.
7.A
【分析】
对k分类讨论,明确集合M,N的范围,即可得到结果.
【详解】
解:∵k∈Z;
∴k=2n或2n+1,n∈Z;
∴;
又;
∴M N.
故选A.
【点睛】
本题考查描述法表示集合的方法,集合间的关系及交并运算,属于基础题.
8.B
【分析】
由函数的最值求出A,由周期求出ω,由特殊点求出φ的值,可得凹函数f(x)的解析式,再利用y=的图象变换规律,得出结论.
【详解】
由函数f(x)=的部分图象,
可得A=2,∵,∴T=π,ω=2,f(x)=2sin(2x+φ),
将代入得,∵﹣π<φ<0,
∴.
故可将函数y=f(x)的图象向左平移个单位长度得到的图象,即为的图象,
故选B.
【点睛】
由的图象变换出 的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换,利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现无论哪种变形,请切记每一个变换总是对字母而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少.
9.C
【分析】
先根据函数的最大值和最小值求得和,然后利用图象求得函数的周期,求得,最后根据时取最大值,求得.
【详解】
解:如图根据函数的最大值和最小值得求得
函数的周期为,即
当时取最大值,即
故选C.
【点睛】
本题主要考查了由的部分图象确定其解析式.考查了学生基础知识的运用和图象观察能力.
10.C
【分析】
利用诱导公式、函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,判断各个选项是否正确,从而得出结论.
【详解】
将函数图象上所有点的横坐标缩短为原来的,
可得y=2sin(2x)的图象,
然后纵坐标不变,再向右平移个单位长度,
得到函数y=g(x)=2sin(2x)=2cos2x的图象,
令x,求得g(x)=0,
可得(,0)是g(x)的一个对称中心,故排除A;
令x,求得g(x)=﹣1,
可得x是g(x)的图象的一条对称轴,故排除B,故C正确;
令x,求得g(x),可得x不是g(x)的图象的对称中心,故排除D,
故选C.
【点睛】
本题主要考查诱导公式、函数y=Asin(ωx+φ)的图象变换规律,以及正弦函数、余弦函数的图象的对称性,属于基础题.
11.
【分析】
利用诱导公式计算即可.
【详解】
解:.
故答案为:.
【点睛】
本题考查诱导公式的应用,是基础题.
12.10
【分析】
利用三角函数的定义式,可以求得,再利用齐次式得到答案.
【详解】
根据角的终边过,利用三角函数的定义式,可以求得
所以有,
故答案是10.
【点睛】
本题考查了三角函数的定义,齐次式,分式上下同时除以转化为是解题的关键.
13.
【分析】
根据所给的图象,得到三角函数的振幅,根据函数的图象过点的坐标,代入解析式求出φ,ω,得到函数的解析式
【详解】
根据图象可以看出A=2,
图像过(0,1)∴2sinφ=1,故φ
∵函数的图象过点(,0)
所以=2k,k∈Z,故, k∈Z
由题即
故当k=-1,
∴函数的解析式是.
故答案为
【点睛】
本题考查三角函数的解析式,三角函数基本性质,熟记五点作图法是解题关键,是中档题.
14.
【分析】
①利用函数的图象和性质的应用求出三角形的底和高,进一步求出三角形的面积;
②利用等腰直角三角形的性质的应用求出的最小值.
【详解】
函数,其中,是这两个函数图象的交点,
当时,.
所以函数的交点间的距离为一个周期,高为.
所以:.
如图所示:
①当时,面积的最小值为;
②若存在是等腰直角三角形,利用直角三角形斜边的中线等于斜边的一半,
则, 解得的最小值为.
故答案为:,.
【点睛】
本题主要考查了三角函数的图象和性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.
15.,是正整数且
【分析】
根据最值列出等式求,再根据最高点和最低点对应的月份求周期,并求,以及利用最高点求.
【详解】
由题意可知,解得:,
,解得:,
当时,,
得: ,,
所以的表达式是,是正整数且.
故答案为:,是正整数且
【点睛】
方法点睛:形如 ,一般根据最值求,利用最值,零点对应的自变量的距离求周期和,以及“五点法”中的一个点求.
16.(1)单调递增区间是,;最小正周期;(2)填表见解析;作图见解析;(3)最大值为2,最小值为-1,时取得最小值,时取得最大值.
【分析】
(1)根据正弦函数的图象与性质求出函数的单调递增区间和最小正周期;
(2)列表,描点、连线,画出函数在长度为一个周期的闭区间上的简图;
(3)求出时函数的最大值和最小值,以及对应的值.
【详解】
解:(1)函数,
令,;
解得,;
即,;
所以函数的单调递增区间是,;
最小正周期;
(2)填写表格如下;
0
0 2 0 -2 0 2
用“五点法”画出函数在长度为一个周期的闭区间上的简图为;
(3)时,,,
所以函数在上取得最大值为2,最小值为-1,
且时取得最小值,时取得最大值.
【点睛】
本题考查正弦型函数的性质以及“五点法”作图,本题要掌握基础函数的性质以及整体法的应用,同时熟悉“五点法”作图,考查分析能力以及作图能力,属中档题.
17.(I)(II)
【分析】
(Ⅰ)由图象可知,A=2.可求函数的周期,利用周期公式可求ω的值,又函数f(x)的图象经过点,可得,结合范围,可求,即可得解函数解析式;(Ⅱ)由x∈[0,m],可得:,根据正弦函数的单调性,分类讨论即可得解m的最大值.
【详解】
(Ⅰ)由图象可知,A=2.
因为,
所以T=π.
所以.解得ω=2.
又因为函数f(x)的图象经过点,
所以.
解得.
又因为,
所以.
所以.
(Ⅱ)因为 x∈[0,m],
所以,
当时,即时,f(x)单调递增,
所以f(x)≥f(0)=1,符合题意;
当时,即时,f(x)单调递减,
所以,符合题意;
当时,即时,f(x)单调递减,
所以,不符合题意;
综上,若对于任意的x∈[0,m],有f(x)≥1恒成立,则必有,
所以m的最大值是.
【点睛】
本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数周期公式,正弦函数的图象和性质的综合应用,考查了数形结合思想和转化思想,属于中档题.确定y=Asin(ωx+φ)+b(A>0,ω>0)的步骤和方法:(1)求A,b,确定函数的最大值M和最小值m,则A=,b=;(2)求ω,确定函数的最小正周期T,则可得ω=;(3)求φ,常用的方法有:①代入法:把图象上的一个已知点代入(此时A,ω,b已知)或代入图象与直线y=b的交点求解(此时要注意交点在上升区间上还是在下降区间上).②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:“最大值点”(即图象的“峰点”)时ωx+φ=;“最小值点”(即图象的“谷点”)时ωx+φ=.
18.(Ⅰ);(Ⅱ).
【详解】
(Ⅰ)根据表中已知数据,解得.数据补全如下表:
0
0
5
0
0
且函数表达式为.
(Ⅱ)由(Ⅰ)知 ,得.
因为的对称中心为,.
令,解得,.
由于函数的图象关于点成中心对称,令,
解得,.由可知,当时,取得最小值.
考点:“五点法”画函数在某一个周期内的图象,三角函数的平移变换,三角函数的性质.
19.(1)
(2)
【分析】
(1)由图象的最高点与最低点易于求出这段时间的最大温差;
(2)可由图象直接得出,由周期求得,然后通过特殊点求,则问题解决.
【详解】
解:(1)由题图可知,这段时间的最大温差是.
(2)从题图中可以看出,从6时到14时的图像是函数的半个周期的图像,所以.
因为,所以.
所以.
依题意.
故所求解析式为.
【点睛】
本题主要考查由函数的部分图象确定其解析式的基本方法.属于中档.
20.见解析
【分析】
方案①③与②③,都有周期可求得,再由型函数的对称轴与对称中心求得,即可表示解析式,最后由三角函数的性质求得指定区间的最值;方案①②中,由对称轴与对称中心可构建方程组,分别表示与,利用分类讨论和时的情况,其中若T小于所求区间范围的区间长度,则最值由振幅确定,反之则可由性质求值域.
【详解】
方案一:选①③.由已知,函数的最小正周期,
所以,,所以.
令,得,.
所以的对称轴方程为,.
令,,由,得.
综上,.
因为,所以.
所以当或,即或时,;
当,即时,.
方案二:选②③.由已知,函数的最小正周期,
所以,,所以.
所以,于是,.
由,得.
综上,.
因为,所以.
所以当,即时,;
当,即时,.
方案三:选①②.由已知可知其中一个对称轴与对称中心,
则,解得
因为,则,即或0
当时,
因为,则
当时,,则
又因为区间的区间长度为,所以函数在区间上的最大值为和最小值为,显然时也成立,
当时,
因为,则
当时,,则
此时函数,则其在区间上有,即,故最大值为,最小值为,
当时,,则,所以函数在区间上的最大值为和最小值为,显然时也成立
综上所述,函数和函数在区间上的最大值为和最小值为;函数在区间上最大值为,最小值为.
【点睛】
本题考查由三角函数的性质求解析式,还考查了求指定区间的最值,属于难题.
21.选择见解析:(1);(2).
【分析】
求出函数的最小正周期,可求得的值.
(1)选择①②,求出的值,由条件②可得出关于的等式结合的取值范围,可求得的值,由此可求得函数的解析式;
选择①③,求出的值,由已知条件可得出,求出的取值范围,可求得的值,由此可求得函数的解析式;
选择②③,由条件②可得出关于的等式结合的取值范围,可求得的值,将点的坐标代入函数的解析式,求出的值,可得出函数的解析式;
(2)由可求得的取值范围,结合题意可得出关于实数的不等式,由此可解得实数的取值范围.
【详解】
由于函数图象上两相邻对称轴之间的距离为,
所以的最小正周期,.此时.
(1)选条件①②;因为,所以.
因为图象的一个对称中心为,所以,
因为,所以,此时,所以;
选条件①③:因为,所以.
因为函数的图象过点,则,即,,
因为,即,,所以,,解得.
所以;
选条件②③:因为函数的一个对称中心为,
所以,所以.
因为,所以,此时,所以.
因为函数的图象过点,所以,即,,即,所以.
所以;
(2)因为,所以,
因为图象的对称轴只有一条落在区间上,所以,得,
所以的取值范围为.
【点睛】
思路点睛:三角函数图象与性质问题的求解思路:
(1)将函数解析式变形为或的形式;
(2)将看成一个整体;
(3)借助正弦函数或余弦函数的图象和性质(如定义域、值域、最值、周期性、对称性、单调性等)解决相关问题.
北京·高一·
三角函数·章节检测
一、选择题(共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项)
1.下列各角中,与角终边相同的是( )
A. B. C. D.
2.已知,那么
A. B. C. D.
3.若,,则是( )
A.第四象限角 B.第三象限角 C.第二象限角 D.第一象限角
4.《九章算术》成书于公元一世纪,是中国古代乃至东方的第一部自成体系的数学专著.书中记载这样一个问题“今有宛田,下周三十步,径十六步.问为田几何?”(一步=1.5米)意思是现有扇形田,弧长为45米,直径为24米,那么扇形田的面积为
A.135平方米 B.270平方米 C.540平方米 D.1080平方米
5.若是的一个内角,且,则的值为
A. B. C. D.
6.将函数的图象上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是
A. B.
C. D.
7.集合M={Z},N={Z},则
A.MN B.NM C.MN= D.MN=R
8.函数的部分图象如图所示,为了得到的图象,只需将函数的图象
A.向左平移个单位长度 B.向左平移个单位长度
C.向右平移个单位长度 D.向右平移个单位长度
9.已知函数的一部分图象如图所示,如果,,,则( )
A. B. C. D.
10.将函数图象上所有点的横坐标缩短为原来的,纵坐标不变,再向右平移个单位长度,得到函数的图象,则下列说法正确的是
A.函数的一条对称轴是
B.函数的一个对称中心是
C.函数的一条对称轴是
D.函数的一个对称中心是
二、填空题(共5小题,每小题5分,共25分)
11.已知,则______.
12.已知角的始边与轴的非负半轴重合,顶点与坐标原点重合,终边过点,则____.
13.已知函数的图象如图所示,则该函数的解析式是__________.
14.已知函数,其中,是这两个函数图像的交点,且不共线.①当时,面积的最小值为___________;②若存在是等腰直角三角形,则的最小值为__________.
15.某地区每年各个月份的月平均最高气温近似地满足周期性规律,因此第个月的月平均最高气温可近似地用函数来刻画,其中正整数表示月份且,例如表示1月份,和是正整数,,.统计发现,该地区每年各个月份的月平均最高气温有以下规律:
①该地区月平均最高气温最高的7月份与最低的1月份相差30摄氏度;
②1月份该地区月平均最高气温为3摄氏度,随后逐月递增直到7月份达到最高;
③每年相同的月份,该地区月平均最高气温基本相同.
根据已知信息,得到的表达式是______.
三、解答题(共6小题,共85分。解答应写出文字说明、演算步骤或证明过程)
16.函数.
(1)求函数的单调递增区间和最小正周期;
(2)请用“五点法”画出函数在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
0
(3)求函数在上的最大值和最小值,并指出相应的的值.
17.已知函数f(x)=Asin(ωx+)(A>0,ω>0,||<)的部分图象如图所示.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若对于任意的x∈[0,m],f(x)≥1恒成立,求m的最大值.
18.某同学用“五点法”画函数在某一个周期内的图象时,列表并填入了部分数据,如下表:
0
0
5
0
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数的解析式;
(Ⅱ)将图象上所有点向左平行移动个单位长度,得到的图象.若图象的一个对称中心为,求的最小值.
19.如图所示,某地一天从6时至14时的温度变化曲线近似满足函数,其中,且函数在6时与14时分别取得最小值(最低温度)和最大值(最高温度).
(1)求这段时间的最大温差;
(2)写出这段曲线的函数解析式.
20.现给出三个条件:①函数的图象关于直线对称;②函数的图象关于点对称;③函数的图象上相邻两个最高点的距离为.从中选出两个条件补充在下面的问题中,并以此为依据求解问题.
已知函数(,),_____,_____.求函数在区间上的最大值和最小值.
21.已知函数,且图象的相邻两条对称轴之间的距离为,再从条件①、条件②、条件③中选择两个作为一组已知条件.
(1)确定的解析式;
(2)若图象的对称轴只有一条落在区间上,求a的取值范围.
条件①:的最小值为;
条件②:图象的一个对称中心为;
条件③;的图象经过点.
试卷第4页,共5页
参考答案
1.D
【分析】
写出与终边相同角的集合,取k值得答案.
【详解】
与角终边相同的角的集合为,
取,可得.
∴与角终边相同的是.
故选:D
【点睛】
本小题主要考查终边相同的角,属于基础题.
2.C
【分析】
试题分析:由,得 .故选C.
考点:诱导公式.
3.B
【分析】
根据三角函数的符号,确定终边上的点所处的象限,从而得到结果.
【详解】
则对应第三象限的点,即是第三象限角
本题正确选项:
【点睛】
本题考查各象限内三角函数值的符号,属于基础题.
4.B
【分析】
直接利用扇形面积计算得到答案.
【详解】
根据扇形的面积公式,计算扇形田的面积为Slr45270(平方米).
故选:B.
【点睛】
本题考查了扇形面积,属于简单题.
5.D
【详解】
试题分析:是的一个内角,,又,所以有,故本题的正确选项为D.
考点:三角函数诱导公式的运用.
6.C
【详解】
将函数的图象上所有的点向右平行移动个单位长度,所得函数图象的解析式为y=sin(x-);
再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是.故选C.
7.A
【分析】
对k分类讨论,明确集合M,N的范围,即可得到结果.
【详解】
解:∵k∈Z;
∴k=2n或2n+1,n∈Z;
∴;
又;
∴M N.
故选A.
【点睛】
本题考查描述法表示集合的方法,集合间的关系及交并运算,属于基础题.
8.B
【分析】
由函数的最值求出A,由周期求出ω,由特殊点求出φ的值,可得凹函数f(x)的解析式,再利用y=的图象变换规律,得出结论.
【详解】
由函数f(x)=的部分图象,
可得A=2,∵,∴T=π,ω=2,f(x)=2sin(2x+φ),
将代入得,∵﹣π<φ<0,
∴.
故可将函数y=f(x)的图象向左平移个单位长度得到的图象,即为的图象,
故选B.
【点睛】
由的图象变换出 的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换,利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现无论哪种变形,请切记每一个变换总是对字母而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少.
9.C
【分析】
先根据函数的最大值和最小值求得和,然后利用图象求得函数的周期,求得,最后根据时取最大值,求得.
【详解】
解:如图根据函数的最大值和最小值得求得
函数的周期为,即
当时取最大值,即
故选C.
【点睛】
本题主要考查了由的部分图象确定其解析式.考查了学生基础知识的运用和图象观察能力.
10.C
【分析】
利用诱导公式、函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,判断各个选项是否正确,从而得出结论.
【详解】
将函数图象上所有点的横坐标缩短为原来的,
可得y=2sin(2x)的图象,
然后纵坐标不变,再向右平移个单位长度,
得到函数y=g(x)=2sin(2x)=2cos2x的图象,
令x,求得g(x)=0,
可得(,0)是g(x)的一个对称中心,故排除A;
令x,求得g(x)=﹣1,
可得x是g(x)的图象的一条对称轴,故排除B,故C正确;
令x,求得g(x),可得x不是g(x)的图象的对称中心,故排除D,
故选C.
【点睛】
本题主要考查诱导公式、函数y=Asin(ωx+φ)的图象变换规律,以及正弦函数、余弦函数的图象的对称性,属于基础题.
11.
【分析】
利用诱导公式计算即可.
【详解】
解:.
故答案为:.
【点睛】
本题考查诱导公式的应用,是基础题.
12.10
【分析】
利用三角函数的定义式,可以求得,再利用齐次式得到答案.
【详解】
根据角的终边过,利用三角函数的定义式,可以求得
所以有,
故答案是10.
【点睛】
本题考查了三角函数的定义,齐次式,分式上下同时除以转化为是解题的关键.
13.
【分析】
根据所给的图象,得到三角函数的振幅,根据函数的图象过点的坐标,代入解析式求出φ,ω,得到函数的解析式
【详解】
根据图象可以看出A=2,
图像过(0,1)∴2sinφ=1,故φ
∵函数的图象过点(,0)
所以=2k,k∈Z,故, k∈Z
由题即
故当k=-1,
∴函数的解析式是.
故答案为
【点睛】
本题考查三角函数的解析式,三角函数基本性质,熟记五点作图法是解题关键,是中档题.
14.
【分析】
①利用函数的图象和性质的应用求出三角形的底和高,进一步求出三角形的面积;
②利用等腰直角三角形的性质的应用求出的最小值.
【详解】
函数,其中,是这两个函数图象的交点,
当时,.
所以函数的交点间的距离为一个周期,高为.
所以:.
如图所示:
①当时,面积的最小值为;
②若存在是等腰直角三角形,利用直角三角形斜边的中线等于斜边的一半,
则, 解得的最小值为.
故答案为:,.
【点睛】
本题主要考查了三角函数的图象和性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.
15.,是正整数且
【分析】
根据最值列出等式求,再根据最高点和最低点对应的月份求周期,并求,以及利用最高点求.
【详解】
由题意可知,解得:,
,解得:,
当时,,
得: ,,
所以的表达式是,是正整数且.
故答案为:,是正整数且
【点睛】
方法点睛:形如 ,一般根据最值求,利用最值,零点对应的自变量的距离求周期和,以及“五点法”中的一个点求.
16.(1)单调递增区间是,;最小正周期;(2)填表见解析;作图见解析;(3)最大值为2,最小值为-1,时取得最小值,时取得最大值.
【分析】
(1)根据正弦函数的图象与性质求出函数的单调递增区间和最小正周期;
(2)列表,描点、连线,画出函数在长度为一个周期的闭区间上的简图;
(3)求出时函数的最大值和最小值,以及对应的值.
【详解】
解:(1)函数,
令,;
解得,;
即,;
所以函数的单调递增区间是,;
最小正周期;
(2)填写表格如下;
0
0 2 0 -2 0 2
用“五点法”画出函数在长度为一个周期的闭区间上的简图为;
(3)时,,,
所以函数在上取得最大值为2,最小值为-1,
且时取得最小值,时取得最大值.
【点睛】
本题考查正弦型函数的性质以及“五点法”作图,本题要掌握基础函数的性质以及整体法的应用,同时熟悉“五点法”作图,考查分析能力以及作图能力,属中档题.
17.(I)(II)
【分析】
(Ⅰ)由图象可知,A=2.可求函数的周期,利用周期公式可求ω的值,又函数f(x)的图象经过点,可得,结合范围,可求,即可得解函数解析式;(Ⅱ)由x∈[0,m],可得:,根据正弦函数的单调性,分类讨论即可得解m的最大值.
【详解】
(Ⅰ)由图象可知,A=2.
因为,
所以T=π.
所以.解得ω=2.
又因为函数f(x)的图象经过点,
所以.
解得.
又因为,
所以.
所以.
(Ⅱ)因为 x∈[0,m],
所以,
当时,即时,f(x)单调递增,
所以f(x)≥f(0)=1,符合题意;
当时,即时,f(x)单调递减,
所以,符合题意;
当时,即时,f(x)单调递减,
所以,不符合题意;
综上,若对于任意的x∈[0,m],有f(x)≥1恒成立,则必有,
所以m的最大值是.
【点睛】
本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数周期公式,正弦函数的图象和性质的综合应用,考查了数形结合思想和转化思想,属于中档题.确定y=Asin(ωx+φ)+b(A>0,ω>0)的步骤和方法:(1)求A,b,确定函数的最大值M和最小值m,则A=,b=;(2)求ω,确定函数的最小正周期T,则可得ω=;(3)求φ,常用的方法有:①代入法:把图象上的一个已知点代入(此时A,ω,b已知)或代入图象与直线y=b的交点求解(此时要注意交点在上升区间上还是在下降区间上).②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:“最大值点”(即图象的“峰点”)时ωx+φ=;“最小值点”(即图象的“谷点”)时ωx+φ=.
18.(Ⅰ);(Ⅱ).
【详解】
(Ⅰ)根据表中已知数据,解得.数据补全如下表:
0
0
5
0
0
且函数表达式为.
(Ⅱ)由(Ⅰ)知 ,得.
因为的对称中心为,.
令,解得,.
由于函数的图象关于点成中心对称,令,
解得,.由可知,当时,取得最小值.
考点:“五点法”画函数在某一个周期内的图象,三角函数的平移变换,三角函数的性质.
19.(1)
(2)
【分析】
(1)由图象的最高点与最低点易于求出这段时间的最大温差;
(2)可由图象直接得出,由周期求得,然后通过特殊点求,则问题解决.
【详解】
解:(1)由题图可知,这段时间的最大温差是.
(2)从题图中可以看出,从6时到14时的图像是函数的半个周期的图像,所以.
因为,所以.
所以.
依题意.
故所求解析式为.
【点睛】
本题主要考查由函数的部分图象确定其解析式的基本方法.属于中档.
20.见解析
【分析】
方案①③与②③,都有周期可求得,再由型函数的对称轴与对称中心求得,即可表示解析式,最后由三角函数的性质求得指定区间的最值;方案①②中,由对称轴与对称中心可构建方程组,分别表示与,利用分类讨论和时的情况,其中若T小于所求区间范围的区间长度,则最值由振幅确定,反之则可由性质求值域.
【详解】
方案一:选①③.由已知,函数的最小正周期,
所以,,所以.
令,得,.
所以的对称轴方程为,.
令,,由,得.
综上,.
因为,所以.
所以当或,即或时,;
当,即时,.
方案二:选②③.由已知,函数的最小正周期,
所以,,所以.
所以,于是,.
由,得.
综上,.
因为,所以.
所以当,即时,;
当,即时,.
方案三:选①②.由已知可知其中一个对称轴与对称中心,
则,解得
因为,则,即或0
当时,
因为,则
当时,,则
又因为区间的区间长度为,所以函数在区间上的最大值为和最小值为,显然时也成立,
当时,
因为,则
当时,,则
此时函数,则其在区间上有,即,故最大值为,最小值为,
当时,,则,所以函数在区间上的最大值为和最小值为,显然时也成立
综上所述,函数和函数在区间上的最大值为和最小值为;函数在区间上最大值为,最小值为.
【点睛】
本题考查由三角函数的性质求解析式,还考查了求指定区间的最值,属于难题.
21.选择见解析:(1);(2).
【分析】
求出函数的最小正周期,可求得的值.
(1)选择①②,求出的值,由条件②可得出关于的等式结合的取值范围,可求得的值,由此可求得函数的解析式;
选择①③,求出的值,由已知条件可得出,求出的取值范围,可求得的值,由此可求得函数的解析式;
选择②③,由条件②可得出关于的等式结合的取值范围,可求得的值,将点的坐标代入函数的解析式,求出的值,可得出函数的解析式;
(2)由可求得的取值范围,结合题意可得出关于实数的不等式,由此可解得实数的取值范围.
【详解】
由于函数图象上两相邻对称轴之间的距离为,
所以的最小正周期,.此时.
(1)选条件①②;因为,所以.
因为图象的一个对称中心为,所以,
因为,所以,此时,所以;
选条件①③:因为,所以.
因为函数的图象过点,则,即,,
因为,即,,所以,,解得.
所以;
选条件②③:因为函数的一个对称中心为,
所以,所以.
因为,所以,此时,所以.
因为函数的图象过点,所以,即,,即,所以.
所以;
(2)因为,所以,
因为图象的对称轴只有一条落在区间上,所以,得,
所以的取值范围为.
【点睛】
思路点睛:三角函数图象与性质问题的求解思路:
(1)将函数解析式变形为或的形式;
(2)将看成一个整体;
(3)借助正弦函数或余弦函数的图象和性质(如定义域、值域、最值、周期性、对称性、单调性等)解决相关问题.
北京·高一·
