2021-2022学年人教A版必修一 1.3.1 单调性与最大(小)值 课件(19张PPT)
文档属性
| 名称 | 2021-2022学年人教A版必修一 1.3.1 单调性与最大(小)值 课件(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 878.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 20:09:44 | ||
图片预览



文档简介
(共19张PPT)
函数是描述事物运动变化规律的数学模型,所以有必要了解函数的变化规律。
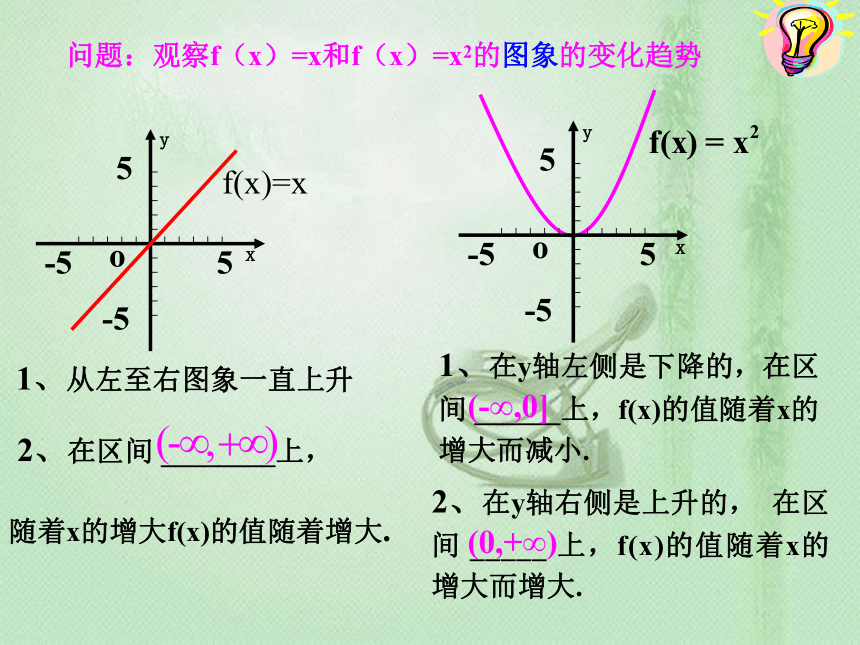
问题:观察f(x)=x和f(x)=x2的图象的变化趋势
o
5
-5
-5
5
f(x)=x
2、在区间 ________上,
随着x的增大f(x)的值随着增大.
1、从左至右图象一直上升
o
5
-5
-5
5
1、在y轴左侧是下降的,在区间 ______上,f(x)的值随着x的增大而减小.
2、在y轴右侧是上升的, 在区间 _____ 上,f(x)的值随着x的增大而增大.
(-∞,0]
(0,+∞)
x
x
y
y
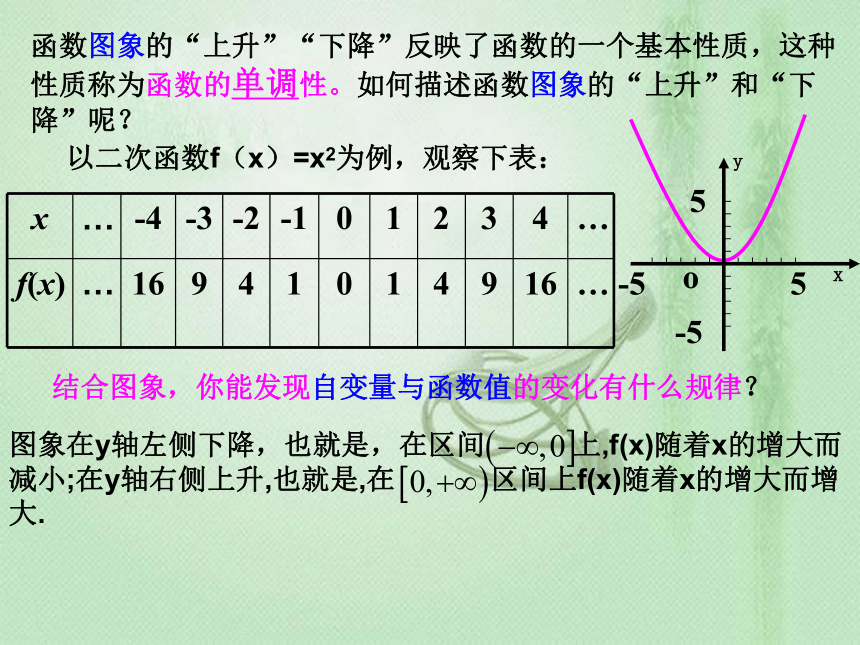
函数图象的“上升”“下降”反映了函数的一个基本性质,这种性质称为函数的单调性。如何描述函数图象的“上升”和“下降”呢?
以二次函数f(x)=x2为例,观察下表:
x … -4 -3 -2 -1 0 1 2 3 4 …
f(x) … 16 9 4 1 0 1 4 9 16 …
结合图象,你能发现自变量与函数值的变化有什么规律?
o
5
-5
-5
5
x
y
图象在y轴左侧下降,也就是,在区间 上,f(x)随着x的增大而减小;在y轴右侧上升,也就是,在 区间上f(x)随着x的增大而增大.
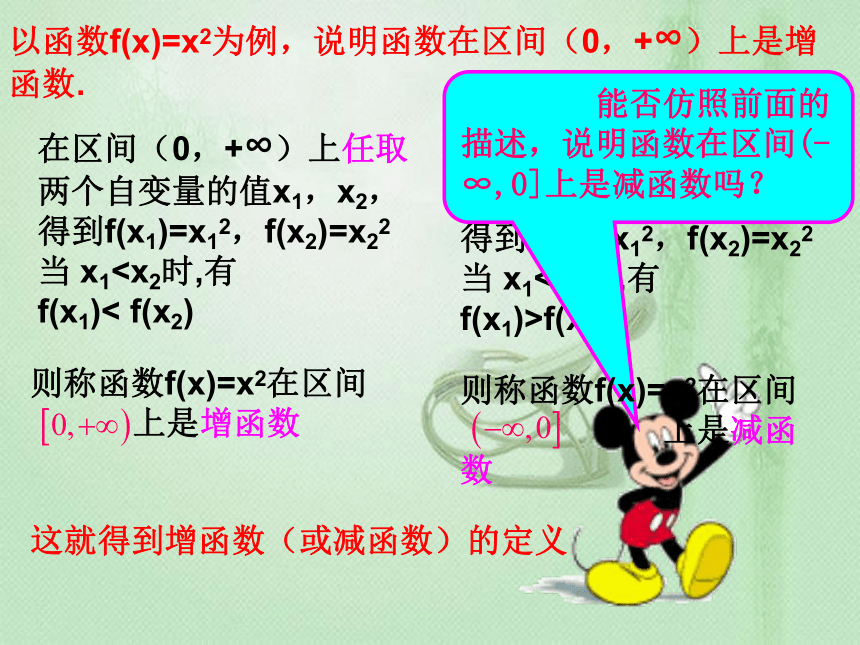
在区间(0,+∞)上任取两个自变量的值x1,x2,得到f(x1)=x12,f(x2)=x22 当 x1在区间(-∞,0)上任取两个自变量的值x1,x2,得到f(x1)=x12,f(x2)=x22 当 x1f(x2)
能否仿照前面的描述,说明函数在区间(-∞,0]上是减函数吗?
以函数f(x)=x2为例,说明函数在区间(0,+∞)上是增函数.
则称函数f(x)=x2在区间
上是增函数
则称函数f(x)=x2在区间
上是减函数
这就得到增函数(或减函数)的定义
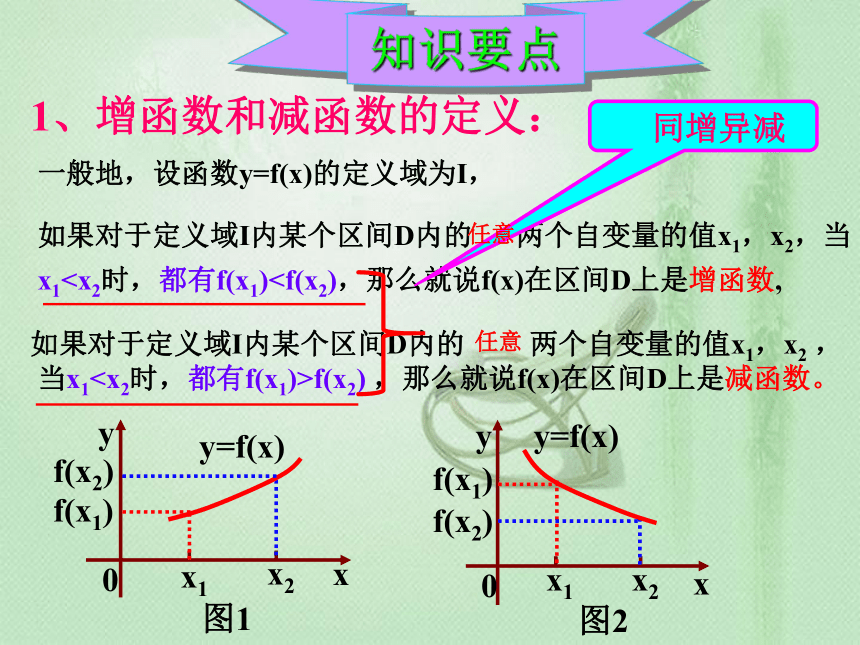
1、增函数和减函数的定义:
一般地,设函数y=f(x)的定义域为I,
如果对于定义域I内某个区间D内的 两个自变量的值x1,x2,当x1知识要点
如果对于定义域I内某个区间D内的 两个自变量的值x1,x2 ,
当x1f(x2) ,那么就说f(x)在区间D上是减函数。
同增异减
任意
任意
y
x
0
x1
x2
f(x1)
f(x2)
y=f(x)
图1
y
x
0
x1
x2
f(x1)
f(x2)
y=f(x)
图2
如果函数y=f(x)在区间D上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
2、单调性、单调区间的定义
1、单调性是对定义域内某个区间而言的,
离开了定义域和相应区间就谈不上单调性.
2 、对于某个具体函数的单调区间,可以是整个定义域(如一次函数),可以是定义域内某个区间(如二次函数).
注意
例1 下图是定义在区间[-5,5]上的函数y=f (x),根据图像说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?
解:函数y=f(x)的单调区间有
[-5,-2),[-2,1),[1,3),[3,5],
其中y=f (x)在区间[-2,1), [3,5]上是增函数,在区间[-5,-2), [1,3)上是减函数.
多个单调区间用逗号隔开
探 究
1. 求函数 y=|2x-1| 的单调区间.
2. 函数f(x)=|x|(2-x)的单调增区间是_________,
单调减区间是_____________________.
x
y
o
1
2
f(x)=
x(2-x), x>0
-x(2-x), x<0
x
y
o
1
2
单调递减区间是(-∞, ]
单调递增区间是( ,+∞ )
1
2
1
2
(-∞,0], [1 ,+∞ )
(0,1)
例2 物理学中的玻意耳定律
告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大,试用函数单调性证明之.
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1由V1,V2∈ (0,+∞)且V10, V2- V1 >0
又k>0,于是
所以,函数 是减函数.也就是说,当体积V减少时,压强p将增大.
取值
定号
作差变形
结论
证明单调性先明确定义域
用定义证明函数单调性的步骤是:
(1)取值
(2)作差变形
(3)定号
(4)判断,下结论
根据单调性的定义得结论
即取 是该区间内的任意两个值且
即求 ,变形的方法主要有因式分解、配方、有理化等
即根据给定的区间和 的符号,确定
的符号
求证:函数 在区间 上是单调递增函数.
则
证明:在区间(0,+∞)上任取两个值 且
又∵0即函数 在区间(0,+∞)上是单调增函数.
∴ f(x1)思考
若把区间改为 ,结论变化吗
若把函数改为
结论变化吗?
巩固练习
例4:已知:f(x)是定义在[-1,1]上的增函
数,且f(x-1)解:由已知得:
解析:直线y=kx+b在k<0时,单调递减.
∴2a-1<0,即a<
D
2.函数 的单调递增区间是___________.
(1,+∞)
3.函数 f(x)=x2-2ax+3在(-∞,4]上是减函数,则
a的取值范围为________.
[4,+∞)
4.根据下图说出函数的单调区间,以及在每一个单调区间上,函数是增函数还是减函数.
解:函数的单调区间是[-1,0),[0,2),[2,4),[4,5].
在区间[-1,0),[2,4)上,函数是减函数;
在区间[0,2),[4,5]上,函数是增函数.
1.增函数和减函数的定义:
一般地,设函数y=f(x)的定义域为I,
如果对于定义域I内某个区间D内的任意两个自变量的值x1,x2,当x1如果对于定义域I内某个区间D内的任意两个自变量的值x1,x2 ,当x1f(x2) ,那么就说f(x)在区间D上是减函数。
3. 证明函数的单调性的基本步骤是:
(1)取值; (2)作差变形;
(3)定号; (4)判断,下结论.
2.函数的单调性是函数在其定义域上的“局部”性质,即函数可能在其定义域上的某个区间内递增,在另外的区间上递减,研究函数的单调性一定要注意在定义域的哪个区间内.
思考题1:讨论函数
的单调性,并证明.
思考题2:若函数 在区间
上是单调递增函数,求实数 的取值范围.
作业:阳光课堂第10页
函数是描述事物运动变化规律的数学模型,所以有必要了解函数的变化规律。
问题:观察f(x)=x和f(x)=x2的图象的变化趋势
o
5
-5
-5
5
f(x)=x
2、在区间 ________上,
随着x的增大f(x)的值随着增大.
1、从左至右图象一直上升
o
5
-5
-5
5
1、在y轴左侧是下降的,在区间 ______上,f(x)的值随着x的增大而减小.
2、在y轴右侧是上升的, 在区间 _____ 上,f(x)的值随着x的增大而增大.
(-∞,0]
(0,+∞)
x
x
y
y
函数图象的“上升”“下降”反映了函数的一个基本性质,这种性质称为函数的单调性。如何描述函数图象的“上升”和“下降”呢?
以二次函数f(x)=x2为例,观察下表:
x … -4 -3 -2 -1 0 1 2 3 4 …
f(x) … 16 9 4 1 0 1 4 9 16 …
结合图象,你能发现自变量与函数值的变化有什么规律?
o
5
-5
-5
5
x
y
图象在y轴左侧下降,也就是,在区间 上,f(x)随着x的增大而减小;在y轴右侧上升,也就是,在 区间上f(x)随着x的增大而增大.
在区间(0,+∞)上任取两个自变量的值x1,x2,得到f(x1)=x12,f(x2)=x22 当 x1
能否仿照前面的描述,说明函数在区间(-∞,0]上是减函数吗?
以函数f(x)=x2为例,说明函数在区间(0,+∞)上是增函数.
则称函数f(x)=x2在区间
上是增函数
则称函数f(x)=x2在区间
上是减函数
这就得到增函数(或减函数)的定义
1、增函数和减函数的定义:
一般地,设函数y=f(x)的定义域为I,
如果对于定义域I内某个区间D内的 两个自变量的值x1,x2,当x1
如果对于定义域I内某个区间D内的 两个自变量的值x1,x2 ,
当x1
同增异减
任意
任意
y
x
0
x1
x2
f(x1)
f(x2)
y=f(x)
图1
y
x
0
x1
x2
f(x1)
f(x2)
y=f(x)
图2
如果函数y=f(x)在区间D上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
2、单调性、单调区间的定义
1、单调性是对定义域内某个区间而言的,
离开了定义域和相应区间就谈不上单调性.
2 、对于某个具体函数的单调区间,可以是整个定义域(如一次函数),可以是定义域内某个区间(如二次函数).
注意
例1 下图是定义在区间[-5,5]上的函数y=f (x),根据图像说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?
解:函数y=f(x)的单调区间有
[-5,-2),[-2,1),[1,3),[3,5],
其中y=f (x)在区间[-2,1), [3,5]上是增函数,在区间[-5,-2), [1,3)上是减函数.
多个单调区间用逗号隔开
探 究
1. 求函数 y=|2x-1| 的单调区间.
2. 函数f(x)=|x|(2-x)的单调增区间是_________,
单调减区间是_____________________.
x
y
o
1
2
f(x)=
x(2-x), x>0
-x(2-x), x<0
x
y
o
1
2
单调递减区间是(-∞, ]
单调递增区间是( ,+∞ )
1
2
1
2
(-∞,0], [1 ,+∞ )
(0,1)
例2 物理学中的玻意耳定律
告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大,试用函数单调性证明之.
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1
又k>0,于是
所以,函数 是减函数.也就是说,当体积V减少时,压强p将增大.
取值
定号
作差变形
结论
证明单调性先明确定义域
用定义证明函数单调性的步骤是:
(1)取值
(2)作差变形
(3)定号
(4)判断,下结论
根据单调性的定义得结论
即取 是该区间内的任意两个值且
即求 ,变形的方法主要有因式分解、配方、有理化等
即根据给定的区间和 的符号,确定
的符号
求证:函数 在区间 上是单调递增函数.
则
证明:在区间(0,+∞)上任取两个值 且
又∵0
∴ f(x1)
若把区间改为 ,结论变化吗
若把函数改为
结论变化吗?
巩固练习
例4:已知:f(x)是定义在[-1,1]上的增函
数,且f(x-1)
解析:直线y=kx+b在k<0时,单调递减.
∴2a-1<0,即a<
D
2.函数 的单调递增区间是___________.
(1,+∞)
3.函数 f(x)=x2-2ax+3在(-∞,4]上是减函数,则
a的取值范围为________.
[4,+∞)
4.根据下图说出函数的单调区间,以及在每一个单调区间上,函数是增函数还是减函数.
解:函数的单调区间是[-1,0),[0,2),[2,4),[4,5].
在区间[-1,0),[2,4)上,函数是减函数;
在区间[0,2),[4,5]上,函数是增函数.
1.增函数和减函数的定义:
一般地,设函数y=f(x)的定义域为I,
如果对于定义域I内某个区间D内的任意两个自变量的值x1,x2,当x1
3. 证明函数的单调性的基本步骤是:
(1)取值; (2)作差变形;
(3)定号; (4)判断,下结论.
2.函数的单调性是函数在其定义域上的“局部”性质,即函数可能在其定义域上的某个区间内递增,在另外的区间上递减,研究函数的单调性一定要注意在定义域的哪个区间内.
思考题1:讨论函数
的单调性,并证明.
思考题2:若函数 在区间
上是单调递增函数,求实数 的取值范围.
作业:阳光课堂第10页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
