人教版五年级上册6.3《梯形的面积》导学精练
文档属性
| 名称 | 人教版五年级上册6.3《梯形的面积》导学精练 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版五年级上册6.3《梯形的面积》导学精练
填一填
1.教材第95页情境图。
(1)拼摆法。
①两个( )的梯形能拼成一个平行四边形。
②梯形的( )等于平行四边形的( ),梯形的高等于平行四边形的( ),一个梯形的面积等于拼成的平行四边形面积的( )。
③
(2)分割法。
①将一个梯形分割成两个( )形。
梯形的面积=三角形①的面积+三角形②的面积
=( )×( )÷2+( )×( )÷2
=( + )×( )÷( )
②将一个梯形分割成一个( )形和一个( )形。
梯形的面积=( )形面积+( )形面积
=( )+( )
=( + )×( )÷( )
(3)梯形的面积= ,如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式用字母表示为 。
2.教材第96页例3。
(1)我国三峡水电站大坝的横截面的一部分是( ),要求它的面积,也就是求( )的面积。
(2)已知梯形上底、下底和高,代入面积公式计算。
S=( )=( + )×( )÷( )=( )(m2)
一、教材第96页问题:怎样求梯形的面积?
1、四人一个小组,学习96内容,拼一拼,说一说。
2、填一填:
1)拼成的平行四边形的底是梯形的( );
2)拼成的平行四边形的高是梯形的( );
3)拼成的平行四边形的面积是( )。
4)梯形的面积是平行四边形面积的( )。
5)一个梯形的面积是拼得的平行四边形面积的( )。
6)梯形的面积=( ),用字母表示为( )。
二、一辆汽车侧面的两块玻璃的形状是梯形(如下图),他们的面积分别是多少?
【方法宝典】
梯形的面积=(上底+下底)×高÷2
用字母表示:S=(a+b)h÷2
一、填空。
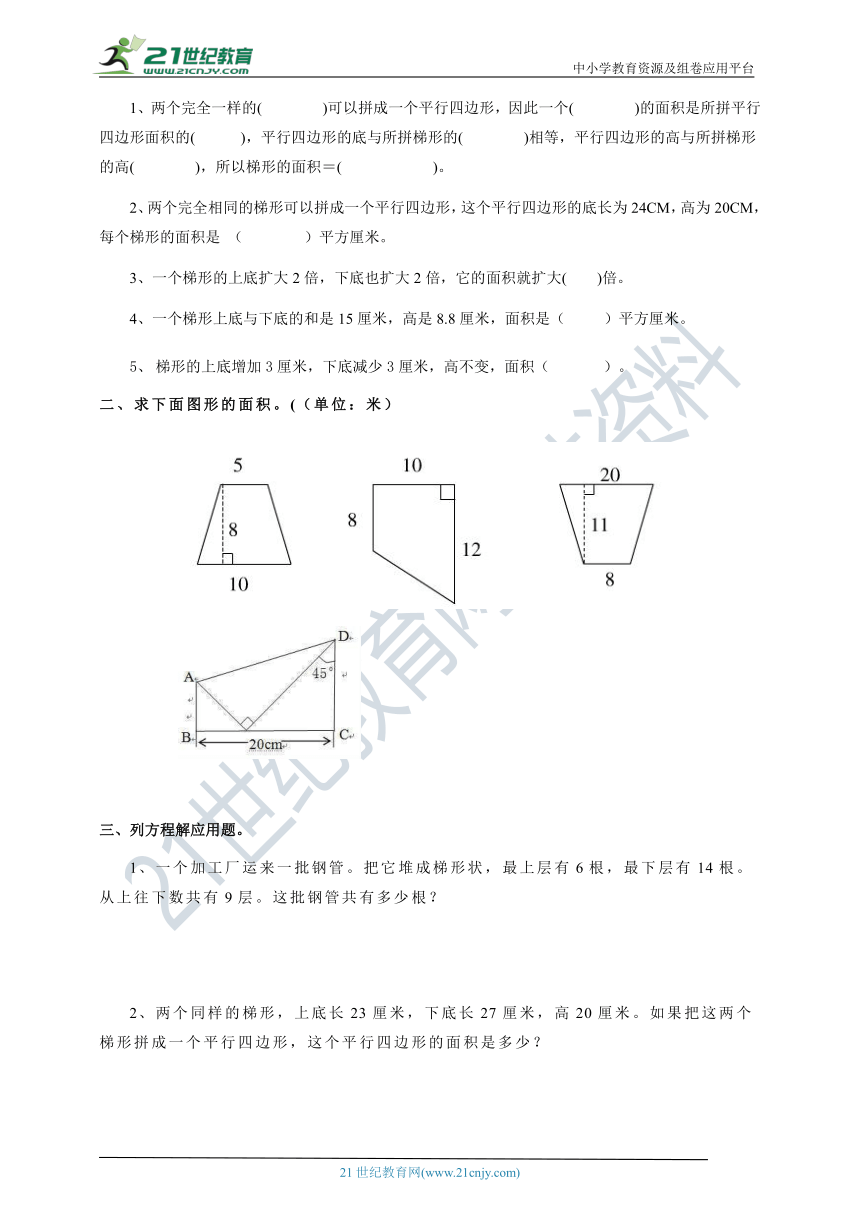
1、两个完全一样的( )可以拼成一个平行四边形,因此一个( )的面积是所拼平行四边形面积的( ),平行四边形的底与所拼梯形的( )相等,平行四边形的高与所拼梯形的高( ),所以梯形的面积=( )。
2、两个完全相同的梯形可以拼成一个平行四边形,这个平行四边形的底长为24CM,高为20CM,每个梯形的面积是 ( )平方厘米。
3、一个梯形的上底扩大2倍,下底也扩大2倍,它的面积就扩大( )倍。
4、一个梯形上底与下底的和是15厘米,高是8.8厘米,面积是( )平方厘米。
5、 梯形的上底增加3厘米,下底减少3厘米,高不变,面积( )。
二、求下面图形的面积。((单位:米)
?
三、列方程解应用题。
1、一个加工厂运来一批钢管。把它堆成梯形状,最上层有6根,最下层有14根。从上往下数共有9层。这批钢管共有多少根?
2、两个同样的梯形,上底长23厘米,下底长27厘米,高20厘米。如果把这两个梯形拼成一个平行四边形,这个平行四边形的面积是多少?
参考答案
课前预习
1.(1)①完全相同 ②上底加下底 底 高 一半
(2)①三角 上底 高 下底 高 上底 下底 高
2 ②平行四边 三角 平行四边 三角 上底×高
(下底-上底)×高÷2 上底 下底 高 2
(3)(上底+下底)×高 ÷2 S=(a+b)×h÷2
2.(1)梯形 梯形
(3)(a+b)×h÷2 36 120 135 2 10530
课堂小练笔
一、填空。
1、梯形 梯形 一半 上底与下底的和 相等
(上底+下底)×高÷2
解析:根据梯形面积的推导过程,可知。
2、240
解析:根据题意是两个完全相同的梯形可以拼成一个平行四边形,所以梯形的面就是平行四边形面积的一半,平行四边形的面积=底×高,计算得到480平方厘米,所以梯形的面积是240平方厘米。
3、2
解析:根据梯形的面积=(上底+下底)×高÷2,上底和下底都扩大2倍,就是(上底+下底)扩大2倍,所以梯形的面积也扩大2倍。
4、66
解析:根据梯形的面积=(上底+下底)×高÷2,因为上底与下底的和是15厘米,所以面积=15×高÷2,计算得到66平方厘米。
5、不变
解析:根据梯形的面积=(上底+下底)×高÷2。梯形的上底增加3厘米,下底
减少3厘米,他们的和没有变。高也不变,所以面积也不变。
二、求下面图形的面积。((单位:厘米)
(5+10)×8÷2=60(平方厘米)
(8+12)×10÷2=100(平方厘米)
(8+20)×11÷2=154(平方厘米) ?
三、列方程解应用题。
1、(6+14)×9÷2=20×9÷2=90(根)
答:这堆钢管共有90根
解析:根据钢管根数=(顶层根数+底层根数)×层数÷2,计算得到90根。
2、(23+27)×20=1000(平方厘米)
答:这个平行四边形的面积是1000平方厘米。
解析:根据梯形面积的推导过程可知,这个平行四边形的面积是梯形面积的2倍。可以直接求出平行四边形的面积。
课前预习
课堂导学
课堂小练笔uxiao’li’a’b
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版五年级上册6.3《梯形的面积》导学精练
填一填
1.教材第95页情境图。
(1)拼摆法。
①两个( )的梯形能拼成一个平行四边形。
②梯形的( )等于平行四边形的( ),梯形的高等于平行四边形的( ),一个梯形的面积等于拼成的平行四边形面积的( )。
③
(2)分割法。
①将一个梯形分割成两个( )形。
梯形的面积=三角形①的面积+三角形②的面积
=( )×( )÷2+( )×( )÷2
=( + )×( )÷( )
②将一个梯形分割成一个( )形和一个( )形。
梯形的面积=( )形面积+( )形面积
=( )+( )
=( + )×( )÷( )
(3)梯形的面积= ,如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式用字母表示为 。
2.教材第96页例3。
(1)我国三峡水电站大坝的横截面的一部分是( ),要求它的面积,也就是求( )的面积。
(2)已知梯形上底、下底和高,代入面积公式计算。
S=( )=( + )×( )÷( )=( )(m2)
一、教材第96页问题:怎样求梯形的面积?
1、四人一个小组,学习96内容,拼一拼,说一说。
2、填一填:
1)拼成的平行四边形的底是梯形的( );
2)拼成的平行四边形的高是梯形的( );
3)拼成的平行四边形的面积是( )。
4)梯形的面积是平行四边形面积的( )。
5)一个梯形的面积是拼得的平行四边形面积的( )。
6)梯形的面积=( ),用字母表示为( )。
二、一辆汽车侧面的两块玻璃的形状是梯形(如下图),他们的面积分别是多少?
【方法宝典】
梯形的面积=(上底+下底)×高÷2
用字母表示:S=(a+b)h÷2
一、填空。
1、两个完全一样的( )可以拼成一个平行四边形,因此一个( )的面积是所拼平行四边形面积的( ),平行四边形的底与所拼梯形的( )相等,平行四边形的高与所拼梯形的高( ),所以梯形的面积=( )。
2、两个完全相同的梯形可以拼成一个平行四边形,这个平行四边形的底长为24CM,高为20CM,每个梯形的面积是 ( )平方厘米。
3、一个梯形的上底扩大2倍,下底也扩大2倍,它的面积就扩大( )倍。
4、一个梯形上底与下底的和是15厘米,高是8.8厘米,面积是( )平方厘米。
5、 梯形的上底增加3厘米,下底减少3厘米,高不变,面积( )。
二、求下面图形的面积。((单位:米)
?
三、列方程解应用题。
1、一个加工厂运来一批钢管。把它堆成梯形状,最上层有6根,最下层有14根。从上往下数共有9层。这批钢管共有多少根?
2、两个同样的梯形,上底长23厘米,下底长27厘米,高20厘米。如果把这两个梯形拼成一个平行四边形,这个平行四边形的面积是多少?
参考答案
课前预习
1.(1)①完全相同 ②上底加下底 底 高 一半
(2)①三角 上底 高 下底 高 上底 下底 高
2 ②平行四边 三角 平行四边 三角 上底×高
(下底-上底)×高÷2 上底 下底 高 2
(3)(上底+下底)×高 ÷2 S=(a+b)×h÷2
2.(1)梯形 梯形
(3)(a+b)×h÷2 36 120 135 2 10530
课堂小练笔
一、填空。
1、梯形 梯形 一半 上底与下底的和 相等
(上底+下底)×高÷2
解析:根据梯形面积的推导过程,可知。
2、240
解析:根据题意是两个完全相同的梯形可以拼成一个平行四边形,所以梯形的面就是平行四边形面积的一半,平行四边形的面积=底×高,计算得到480平方厘米,所以梯形的面积是240平方厘米。
3、2
解析:根据梯形的面积=(上底+下底)×高÷2,上底和下底都扩大2倍,就是(上底+下底)扩大2倍,所以梯形的面积也扩大2倍。
4、66
解析:根据梯形的面积=(上底+下底)×高÷2,因为上底与下底的和是15厘米,所以面积=15×高÷2,计算得到66平方厘米。
5、不变
解析:根据梯形的面积=(上底+下底)×高÷2。梯形的上底增加3厘米,下底
减少3厘米,他们的和没有变。高也不变,所以面积也不变。
二、求下面图形的面积。((单位:厘米)
(5+10)×8÷2=60(平方厘米)
(8+12)×10÷2=100(平方厘米)
(8+20)×11÷2=154(平方厘米) ?
三、列方程解应用题。
1、(6+14)×9÷2=20×9÷2=90(根)
答:这堆钢管共有90根
解析:根据钢管根数=(顶层根数+底层根数)×层数÷2,计算得到90根。
2、(23+27)×20=1000(平方厘米)
答:这个平行四边形的面积是1000平方厘米。
解析:根据梯形面积的推导过程可知,这个平行四边形的面积是梯形面积的2倍。可以直接求出平行四边形的面积。
课前预习
课堂导学
课堂小练笔uxiao’li’a’b
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
