2021--2022学年北师大版八年级数学上册4.1 函数课件(34张)
文档属性
| 名称 | 2021--2022学年北师大版八年级数学上册4.1 函数课件(34张) |  | |
| 格式 | zip | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 21:41:03 | ||
图片预览







文档简介
(共34张PPT)
—4.1 函数
第四章 函数
义务教育教科书
八年级上册
数
学
青岛之旅
青岛之旅
青岛之旅
创设情境 回顾复习
在8:00到9:00
这个时段,高铁以300km/h的速度匀速行驶.
常量是 ,
创设情境 回顾复习
变量是 ,
自变量是 ,
因变量是 .
行驶速度
行驶时间和行驶路程
行驶时间
行驶路程
实例1:摩天轮
实例探究 感知概念
如果你坐在匀速转动的摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?
实例1:摩天轮
实例探究 感知概念
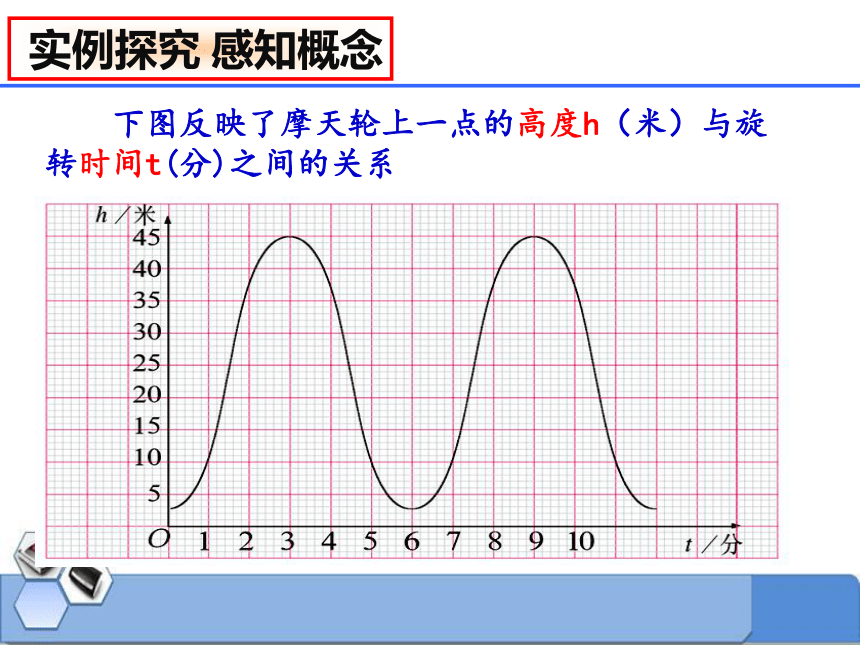
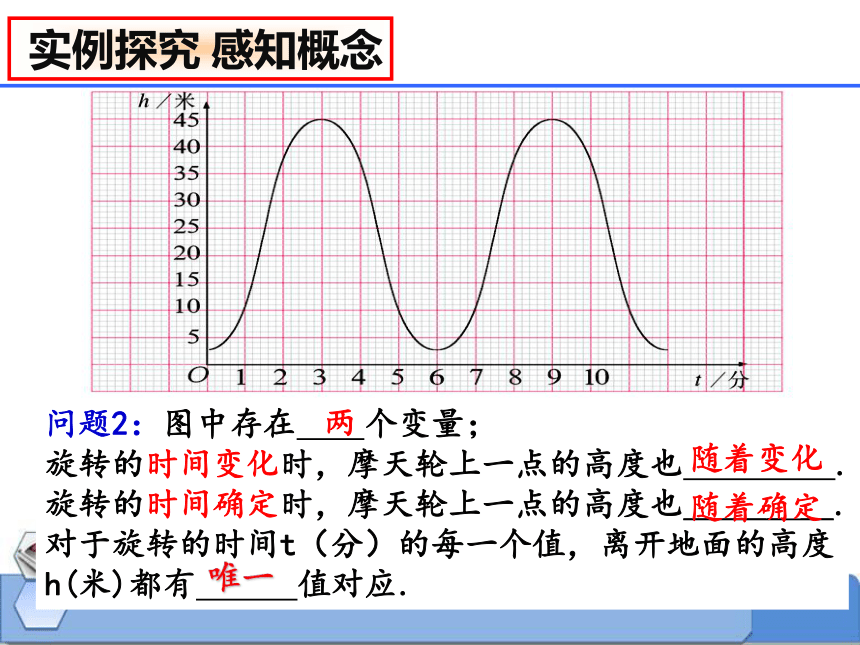
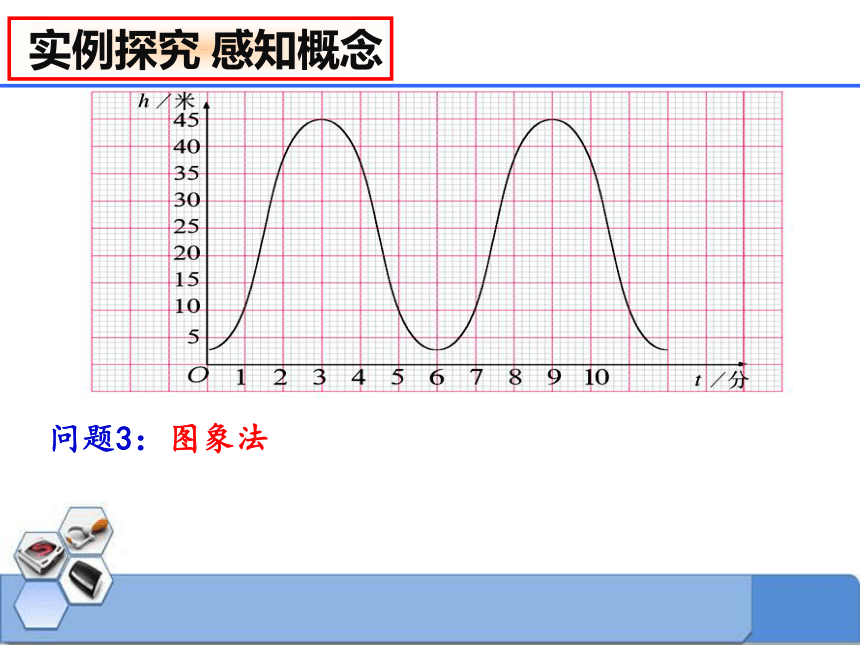
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系
实例探究 感知概念
实例探究 感知概念
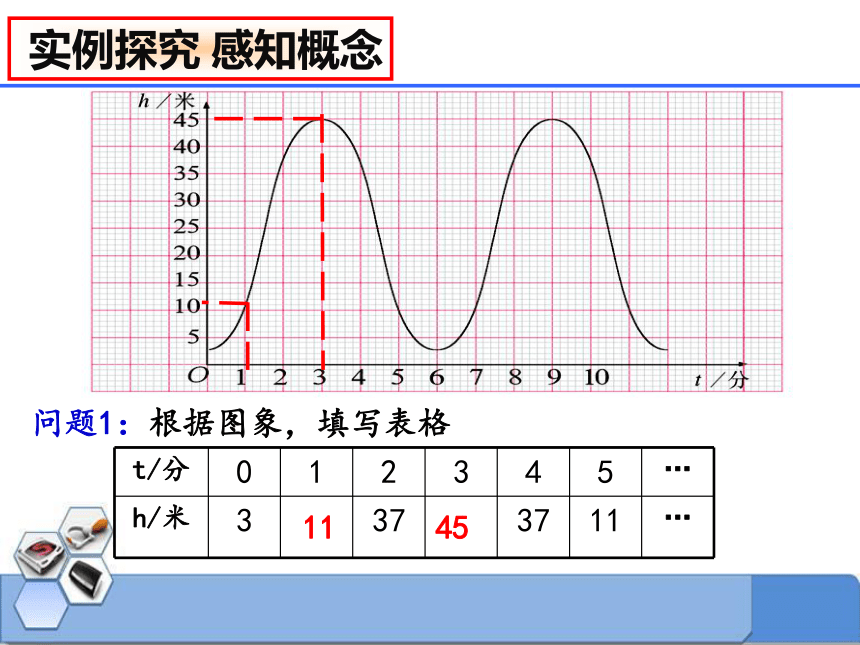
问题1:根据图象,填写表格
t/分 0 1 2 3 4 5 …
h/米 3 37 37 11 …
45
11
实例探究 感知概念
问题2:图中存在 个变量;
旋转的时间变化时,摩天轮上一点的高度也 .
旋转的时间确定时,摩天轮上一点的高度也______ __.
对于旋转的时间t(分)的每一个值,离开地面的高度h(米)都有 值对应.
两
随着变化
随着确定
唯一
实例探究 感知概念
问题3:
图象法
实例探究 感知概念
层数n 1 2 3 4 5 ···
饮料总数m ···
1
3
6
10
15
实例2:饮料堆放
问题1:填表
实例探究 感知概念
实例探究 感知概念
问题2:表格中有_____个变量,
当层数n变化时,饮料总数m也_________;
当层数n确定时,饮料总数m也_________;
对层数n的每一个值,饮料总数m都有 值对应.
两
随着变化
随着确定
唯一
实例探究 感知概念
问题3:
列表法
实例探究 感知概念
实例探究 感知概念
关系式法
实例3:购买纪念品
已知纪念品10元/套,如果用x(套)表示
购买数量,用y(元)表示需要的总金额.
问题3:
问题1:关系式:
问题2:该关系式中有___个变量.
当购买套数x变化时,总金额y也__________;
当购买套数x确定时,总金额y也__________;
对于购买套数x(套)的每一个值,总金额y(元)都有_________值对应.
y =10x
两
随着变化
唯一
随着确定
归纳总结 形成概念
前面讨论的问题中,有哪些共同点?
函 数
一个变化过程
唯一对应关系
两个变量
函数的概念
一般地, 在一个变化过程中的 个变量x和y, 如果对于x的每一个值, y都有 的值与它对应,那么我们称 是 的函数,其中x是自变量y是 ____ .
唯一
y
两
x
因变量
归纳总结 形成概念
n 1 2 3 4 5 …
m 1 3 6 10 15 …
y=10x
图象法
列表法
关系式法
函数的表示方法
归纳总结 形成概念
灵活运用 巩固概念
灵活运用 巩固概念
有 个变量,
自变量是 ,因变量是 ,
是 的函数.
1.
两
骑行时间
骑行费用
骑行费用
骑行时间
灵活运用 巩固概念
有 个变量,
自变量是 ,因变量是 ,
是 的函数.
2.
两
乘坐站数
票价
票价
乘坐站数
x(站) 1 2 3 4 5 6 7 8 9 10
y(元) 2 2 3 3 4 4 5 6 8 9
灵活运用 巩固概念
3.
速度v
滑行距离s
有 个变量,
自变量是 ,因变量是 ,
是 的函数.
两
滑行距离
速度
滑行距离
速度
上述实际问题中,自变量能取哪些值?
实际问题中应注意自变量的取值范围
拓展延伸 深化概念
拓展延伸 深化概念
下列图形中的曲线不表示y是x的函数的是( )
A
B
C
D
C
拓展延伸 深化概念
下列图形中的曲线不表示y是x的函数的是( )
A
B
C
D
D
拓展延伸 深化概念
下列各式中,y不是x的函数的是( )
B
C
D
C
y=x
y=x2 +1
∣y ∣=x
A
三、注意问题:
一、知识:
二、思想方法:
1.函数概念
2.函数的表示方法:
图象法、列表法、关系式法
数形结合
实际问题中应注意自变量的取值范围
自主归纳 升华概念
变化过程
两个变量
唯一对应
1.下列各组中,是函数关系的是
(1)圆的面积与它的半径;
(2)小明的身高与年龄;
(3)正方形的面积与梯形的面积.
(1)(2)
自我诊断 落实概念
2.(1)当t为0℃相应的热力学温度T是___ T(K);
当t为-43℃,相应的热力学温度T是___ T(K);
当t为274℃相应的热力学温度T是___ T(K).
273
547
230
(2)在这一变化过程中,热力学温度T(K)是摄氏温度t(℃)的函数吗?
是
※3.下列各图中表示y是x的函数的是
自我诊断 落实概念
①
②
③
① ②
必做:1.完成《导学案》上的相关内容
2.预习下一节《4.2 一次函数》
选做:请以《生活中的常量和变量》
为题,写一篇数学小日记。
课后作业
学习的效果与我们的勤奋程度也成函数关系,希望大家通过自己的 勤奋获取学习效果的最大值!
驶向胜利的彼岸
下课了!
再见
老师寄语
—4.1 函数
第四章 函数
义务教育教科书
八年级上册
数
学
青岛之旅
青岛之旅
青岛之旅
创设情境 回顾复习
在8:00到9:00
这个时段,高铁以300km/h的速度匀速行驶.
常量是 ,
创设情境 回顾复习
变量是 ,
自变量是 ,
因变量是 .
行驶速度
行驶时间和行驶路程
行驶时间
行驶路程
实例1:摩天轮
实例探究 感知概念
如果你坐在匀速转动的摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?
实例1:摩天轮
实例探究 感知概念
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系
实例探究 感知概念
实例探究 感知概念
问题1:根据图象,填写表格
t/分 0 1 2 3 4 5 …
h/米 3 37 37 11 …
45
11
实例探究 感知概念
问题2:图中存在 个变量;
旋转的时间变化时,摩天轮上一点的高度也 .
旋转的时间确定时,摩天轮上一点的高度也______ __.
对于旋转的时间t(分)的每一个值,离开地面的高度h(米)都有 值对应.
两
随着变化
随着确定
唯一
实例探究 感知概念
问题3:
图象法
实例探究 感知概念
层数n 1 2 3 4 5 ···
饮料总数m ···
1
3
6
10
15
实例2:饮料堆放
问题1:填表
实例探究 感知概念
实例探究 感知概念
问题2:表格中有_____个变量,
当层数n变化时,饮料总数m也_________;
当层数n确定时,饮料总数m也_________;
对层数n的每一个值,饮料总数m都有 值对应.
两
随着变化
随着确定
唯一
实例探究 感知概念
问题3:
列表法
实例探究 感知概念
实例探究 感知概念
关系式法
实例3:购买纪念品
已知纪念品10元/套,如果用x(套)表示
购买数量,用y(元)表示需要的总金额.
问题3:
问题1:关系式:
问题2:该关系式中有___个变量.
当购买套数x变化时,总金额y也__________;
当购买套数x确定时,总金额y也__________;
对于购买套数x(套)的每一个值,总金额y(元)都有_________值对应.
y =10x
两
随着变化
唯一
随着确定
归纳总结 形成概念
前面讨论的问题中,有哪些共同点?
函 数
一个变化过程
唯一对应关系
两个变量
函数的概念
一般地, 在一个变化过程中的 个变量x和y, 如果对于x的每一个值, y都有 的值与它对应,那么我们称 是 的函数,其中x是自变量y是 ____ .
唯一
y
两
x
因变量
归纳总结 形成概念
n 1 2 3 4 5 …
m 1 3 6 10 15 …
y=10x
图象法
列表法
关系式法
函数的表示方法
归纳总结 形成概念
灵活运用 巩固概念
灵活运用 巩固概念
有 个变量,
自变量是 ,因变量是 ,
是 的函数.
1.
两
骑行时间
骑行费用
骑行费用
骑行时间
灵活运用 巩固概念
有 个变量,
自变量是 ,因变量是 ,
是 的函数.
2.
两
乘坐站数
票价
票价
乘坐站数
x(站) 1 2 3 4 5 6 7 8 9 10
y(元) 2 2 3 3 4 4 5 6 8 9
灵活运用 巩固概念
3.
速度v
滑行距离s
有 个变量,
自变量是 ,因变量是 ,
是 的函数.
两
滑行距离
速度
滑行距离
速度
上述实际问题中,自变量能取哪些值?
实际问题中应注意自变量的取值范围
拓展延伸 深化概念
拓展延伸 深化概念
下列图形中的曲线不表示y是x的函数的是( )
A
B
C
D
C
拓展延伸 深化概念
下列图形中的曲线不表示y是x的函数的是( )
A
B
C
D
D
拓展延伸 深化概念
下列各式中,y不是x的函数的是( )
B
C
D
C
y=x
y=x2 +1
∣y ∣=x
A
三、注意问题:
一、知识:
二、思想方法:
1.函数概念
2.函数的表示方法:
图象法、列表法、关系式法
数形结合
实际问题中应注意自变量的取值范围
自主归纳 升华概念
变化过程
两个变量
唯一对应
1.下列各组中,是函数关系的是
(1)圆的面积与它的半径;
(2)小明的身高与年龄;
(3)正方形的面积与梯形的面积.
(1)(2)
自我诊断 落实概念
2.(1)当t为0℃相应的热力学温度T是___ T(K);
当t为-43℃,相应的热力学温度T是___ T(K);
当t为274℃相应的热力学温度T是___ T(K).
273
547
230
(2)在这一变化过程中,热力学温度T(K)是摄氏温度t(℃)的函数吗?
是
※3.下列各图中表示y是x的函数的是
自我诊断 落实概念
①
②
③
① ②
必做:1.完成《导学案》上的相关内容
2.预习下一节《4.2 一次函数》
选做:请以《生活中的常量和变量》
为题,写一篇数学小日记。
课后作业
学习的效果与我们的勤奋程度也成函数关系,希望大家通过自己的 勤奋获取学习效果的最大值!
驶向胜利的彼岸
下课了!
再见
老师寄语
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
