2021--2022学年华东师大版数学九年级上册24.2.直角三角形的性质 课件(19张)
文档属性
| 名称 | 2021--2022学年华东师大版数学九年级上册24.2.直角三角形的性质 课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 794.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 21:44:16 | ||
图片预览


文档简介
(共19张PPT)
第24章 解直角三角形
24.2 直角三角形的性质
学习目标
1.理解直角三角形及在实际生活中的应用;(重点)
2.经历直角三角形的性质的猜想、演绎推理、证明过程,体会
探究过程中的乐趣.(难点)
回顾与思考
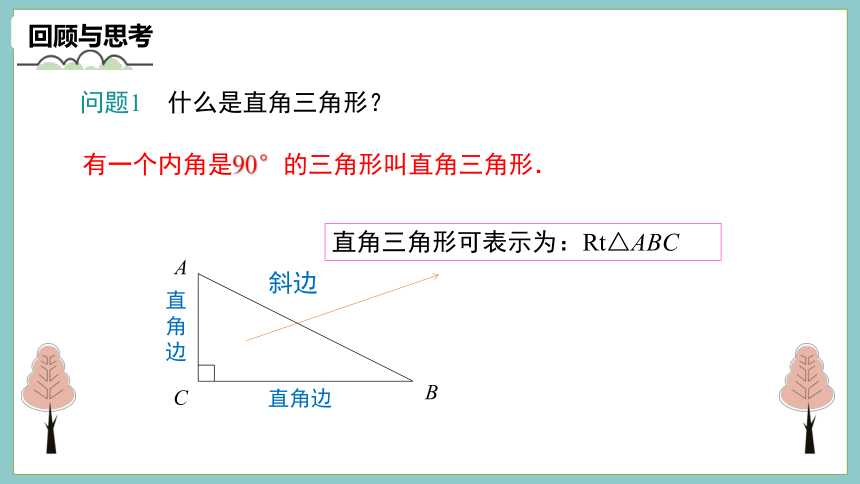
问题1 什么是直角三角形?
直角三角形可表示为:Rt△ABC
A
C
B
斜边
直角边
直角边
有一个内角是90°的三角形叫直角三角形.
A
C
B
C
A
直角三角形的性质
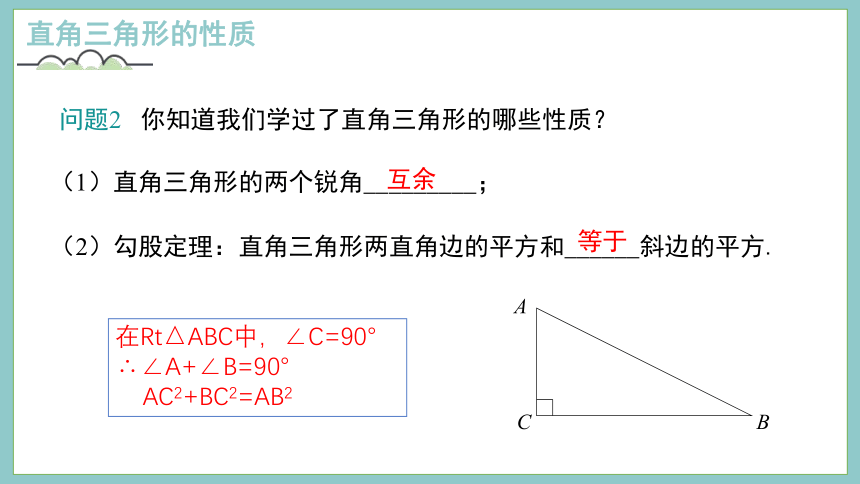
(1)直角三角形的两个锐角_________;
互余
(2)勾股定理:直角三角形两直角边的平方和______斜边的平方.
等于
问题2 你知道我们学过了直角三角形的哪些性质?
在Rt△ABC中,∠C=90°
∴∠A+∠B=90°
AC2+BC2=AB2
知识点
直角三角形斜边上的中线的性质
1
A
B
C
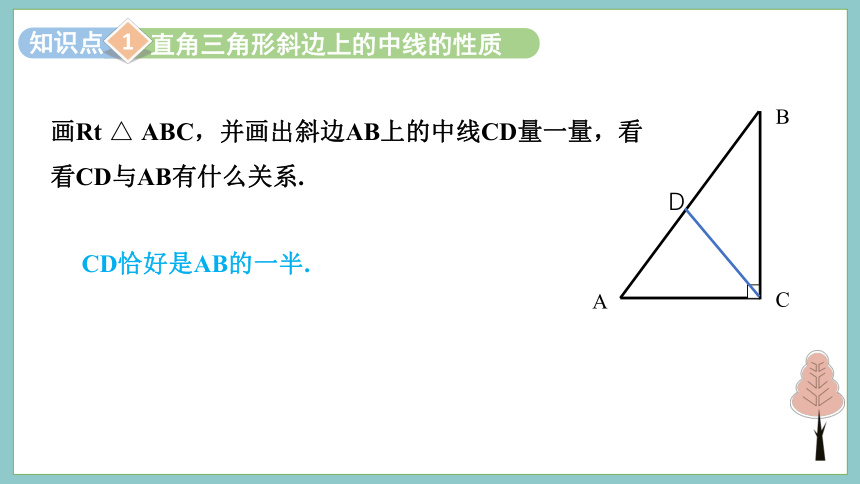
画Rt △ ABC,并画出斜边AB上的中线CD量一量,看看CD与AB有什么关系.
CD恰好是AB的一半.
D
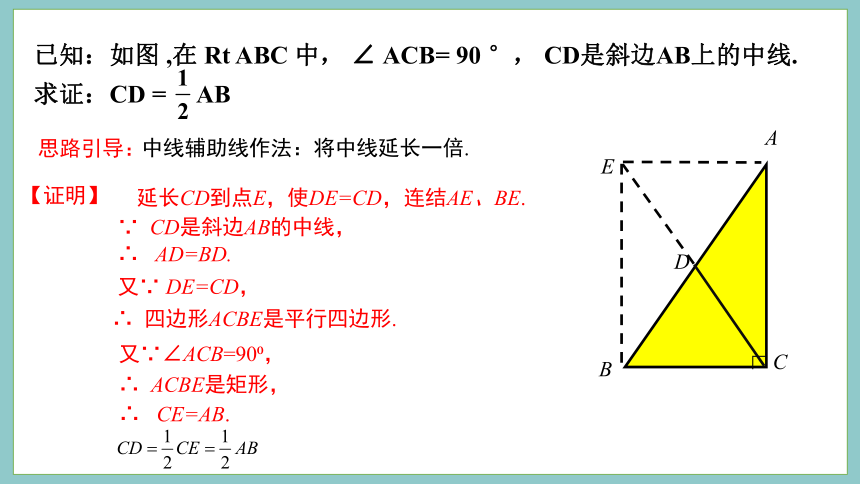
已知:如图 ,在 Rt ABC 中, ∠ ACB= 90 °, CD是斜边AB上的中线. 求证:CD = AB
A
B
C
∟
D
E
思路引导:
中线辅助线作法:将中线延长一倍.
【证明】
∴ ACBE是矩形,
∴ CE=AB.
延长CD到点E,使DE=CD,连结AE、BE.
∵ CD是斜边AB的中线,
∴ AD=BD.
又∵ DE=CD,
∴ 四边形ACBE是平行四边形.
又∵∠ACB=90 ,
知识点
直角三角形斜边上的中线的性质
1
A
B
C
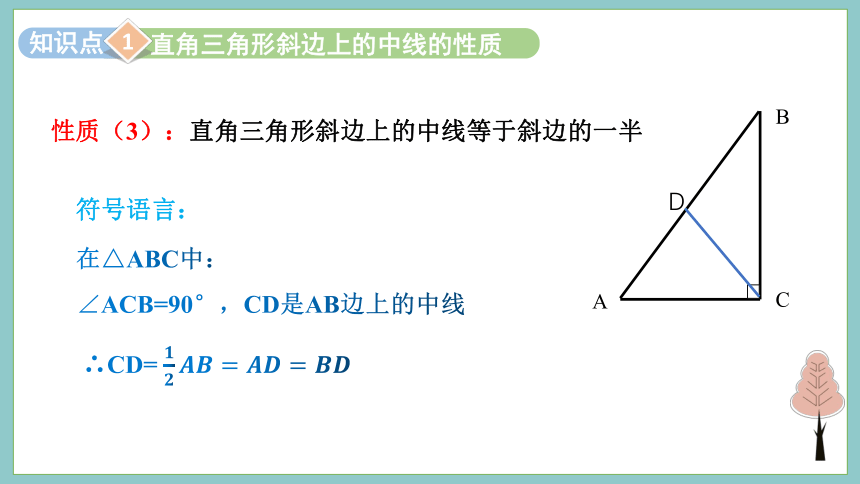
性质(3):直角三角形斜边上的中线等于斜边的一半
符号语言:
D
在△ABC中:
∠ACB=90°,CD是AB边上的中线
∴CD=
已知:CD是△ABC 边AB上的中线,且CD = AB, 求证:∠ ACB= 90 °
A
B
C
D
思考:性质3反之成立吗?
练习1
1.已知Rt△ABC中,斜边AB=10cm,则斜边上的中线的长为______.
2.如图,在Rt△ABC中,CD是斜边AB上的中线∠CDA=80°,则∠A=_____ ,∠B=_____.
5cm
50°
40°
知识归纳
1.直角三角形斜边上的中线把直角三角形分成两个面积相等的等腰三角形.
2. 此性质适用于所有直角三角形,具有一般性,是解决线段倍分关系的重要依据.
练习1
3.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连结DE,则△CDE的周长为________
4.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为__________
第3题图
第4题图
14
练习1
5.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,求四边形ABOM的周长.
解:在矩形ABCD,∵O是AC的中点, M是AD的中点,
∴OM=0.5CD=0.5AB=2.5
AM=0.5AD=6
∵AB=5,BC=AD=12,
∴AC=13(勾股定理),
∵O是矩形ABCD的对角线AC的中点,
∴BO=0.5AC=6.5,
∴四边形ABOM的周长为AB+AM+BO+OM=5+6+6.5+2.5=20.
练习1
6.如图,在△ABC中,BD、CE是高,M、N分别是BC、ED的中点,求证:MN⊥DE.
解:连结EM、DM.
∵BD、CE是高,M是BC中点,
∴在Rt△BCE和Rt△BCD中,
∴EM=DM.
又∵N是ED的中点,∴MN⊥ED
,
,
BC
2
1
DM
BC
2
1
EM
=
=
N
M
D
E
B
C
A
直角三角形30°角的性质
知识点
2
证明: 作斜边上的中线CD,则CD=AD=BD= AB
(在直角三角形中,斜边上的中线等于斜边的一半)
∵ ∠A=30°
∴ ∠B=60°
∴ △CDB是等边三角形,
∴ BC=BD= AB
C
B
A
D
例 Rt△ABC中,∠ACB=90 ° ,∠A=30°,求证:BC= AB.
直角三角形30°角的性质
知识点
2
C
B
A
性质(4):直角三角形中,30°所对的直角边等于斜边的一半
符号语言:
在△ABC中:
∠ACB=90°,∠A=30°
∴BC=
应用此性质,必须满足两个条件:
(1)在直角三角形中;(2)有一个锐角为30°.二者缺一不可.
练习2
1.如图,在△ABC中,若∠BAC=120°,AB=AC, AD⊥AC于点A,BD=3,则BC=______.
9
2.如图, ∠C=90°,∠B=15°,DE垂直平分AB,垂足为点E,交BC边于点D,BD=16cm,则AC的长为______.
8cm
练习2
3.如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是________.
3
4. 等腰三角形的腰长为8cm,底角为15°,则这个三角形的面积为__________
16cm2
练习2
5.如图,△ABC中,∠ACB=90°,∠A=30°,AB=4,CD是△ABC的高,求BD的长
解:∵△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC=0.5AB=0.5×4=2,
∵CD是△ABC的高,
∴∠CDA=∠ACB=90°,
∠B=∠B,
故∠BCD=∠A=30°,
∴在Rt△BCD中,BD=0.5BC=0.5×2=1,
∴BD=1.
课堂小结
性质1
直角三角形两个锐角互余
性质2
直角三角形的勾股定理
性质3
直角三角形斜边上的中线等于斜边的一半
性质4
直角三角形30 角所对直角边等于斜边的一半
完毕·感谢
The user can perform the presentation on a projector or computer, and the powerpoint can be printed out and made into film.
第24章 解直角三角形
24.2 直角三角形的性质
学习目标
1.理解直角三角形及在实际生活中的应用;(重点)
2.经历直角三角形的性质的猜想、演绎推理、证明过程,体会
探究过程中的乐趣.(难点)
回顾与思考
问题1 什么是直角三角形?
直角三角形可表示为:Rt△ABC
A
C
B
斜边
直角边
直角边
有一个内角是90°的三角形叫直角三角形.
A
C
B
C
A
直角三角形的性质
(1)直角三角形的两个锐角_________;
互余
(2)勾股定理:直角三角形两直角边的平方和______斜边的平方.
等于
问题2 你知道我们学过了直角三角形的哪些性质?
在Rt△ABC中,∠C=90°
∴∠A+∠B=90°
AC2+BC2=AB2
知识点
直角三角形斜边上的中线的性质
1
A
B
C
画Rt △ ABC,并画出斜边AB上的中线CD量一量,看看CD与AB有什么关系.
CD恰好是AB的一半.
D
已知:如图 ,在 Rt ABC 中, ∠ ACB= 90 °, CD是斜边AB上的中线. 求证:CD = AB
A
B
C
∟
D
E
思路引导:
中线辅助线作法:将中线延长一倍.
【证明】
∴ ACBE是矩形,
∴ CE=AB.
延长CD到点E,使DE=CD,连结AE、BE.
∵ CD是斜边AB的中线,
∴ AD=BD.
又∵ DE=CD,
∴ 四边形ACBE是平行四边形.
又∵∠ACB=90 ,
知识点
直角三角形斜边上的中线的性质
1
A
B
C
性质(3):直角三角形斜边上的中线等于斜边的一半
符号语言:
D
在△ABC中:
∠ACB=90°,CD是AB边上的中线
∴CD=
已知:CD是△ABC 边AB上的中线,且CD = AB, 求证:∠ ACB= 90 °
A
B
C
D
思考:性质3反之成立吗?
练习1
1.已知Rt△ABC中,斜边AB=10cm,则斜边上的中线的长为______.
2.如图,在Rt△ABC中,CD是斜边AB上的中线∠CDA=80°,则∠A=_____ ,∠B=_____.
5cm
50°
40°
知识归纳
1.直角三角形斜边上的中线把直角三角形分成两个面积相等的等腰三角形.
2. 此性质适用于所有直角三角形,具有一般性,是解决线段倍分关系的重要依据.
练习1
3.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连结DE,则△CDE的周长为________
4.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为__________
第3题图
第4题图
14
练习1
5.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,求四边形ABOM的周长.
解:在矩形ABCD,∵O是AC的中点, M是AD的中点,
∴OM=0.5CD=0.5AB=2.5
AM=0.5AD=6
∵AB=5,BC=AD=12,
∴AC=13(勾股定理),
∵O是矩形ABCD的对角线AC的中点,
∴BO=0.5AC=6.5,
∴四边形ABOM的周长为AB+AM+BO+OM=5+6+6.5+2.5=20.
练习1
6.如图,在△ABC中,BD、CE是高,M、N分别是BC、ED的中点,求证:MN⊥DE.
解:连结EM、DM.
∵BD、CE是高,M是BC中点,
∴在Rt△BCE和Rt△BCD中,
∴EM=DM.
又∵N是ED的中点,∴MN⊥ED
,
,
BC
2
1
DM
BC
2
1
EM
=
=
N
M
D
E
B
C
A
直角三角形30°角的性质
知识点
2
证明: 作斜边上的中线CD,则CD=AD=BD= AB
(在直角三角形中,斜边上的中线等于斜边的一半)
∵ ∠A=30°
∴ ∠B=60°
∴ △CDB是等边三角形,
∴ BC=BD= AB
C
B
A
D
例 Rt△ABC中,∠ACB=90 ° ,∠A=30°,求证:BC= AB.
直角三角形30°角的性质
知识点
2
C
B
A
性质(4):直角三角形中,30°所对的直角边等于斜边的一半
符号语言:
在△ABC中:
∠ACB=90°,∠A=30°
∴BC=
应用此性质,必须满足两个条件:
(1)在直角三角形中;(2)有一个锐角为30°.二者缺一不可.
练习2
1.如图,在△ABC中,若∠BAC=120°,AB=AC, AD⊥AC于点A,BD=3,则BC=______.
9
2.如图, ∠C=90°,∠B=15°,DE垂直平分AB,垂足为点E,交BC边于点D,BD=16cm,则AC的长为______.
8cm
练习2
3.如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是________.
3
4. 等腰三角形的腰长为8cm,底角为15°,则这个三角形的面积为__________
16cm2
练习2
5.如图,△ABC中,∠ACB=90°,∠A=30°,AB=4,CD是△ABC的高,求BD的长
解:∵△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC=0.5AB=0.5×4=2,
∵CD是△ABC的高,
∴∠CDA=∠ACB=90°,
∠B=∠B,
故∠BCD=∠A=30°,
∴在Rt△BCD中,BD=0.5BC=0.5×2=1,
∴BD=1.
课堂小结
性质1
直角三角形两个锐角互余
性质2
直角三角形的勾股定理
性质3
直角三角形斜边上的中线等于斜边的一半
性质4
直角三角形30 角所对直角边等于斜边的一半
完毕·感谢
The user can perform the presentation on a projector or computer, and the powerpoint can be printed out and made into film.
