第4章图形的相似 同步达标测评 2021-2022学年北师大版九年级数学上册(Word版含解析)
文档属性
| 名称 | 第4章图形的相似 同步达标测评 2021-2022学年北师大版九年级数学上册(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 415.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 00:00:00 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学上册《第4章图形的相似》同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.已知,那么下列等式中不成立的是( )
A.4x=3y B. C. D.
2.下列各组的四条线段a,b,c,d是成比例线段的是( )
A.a=4,b=6,c=5,d=10 B.a=1,b=2,c=3,d=4
C.,b=3,c=2, D.a=2,,,
3.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.且AB=3,AC=8,则的值为( )
A. B. C. D.
4.如图,在△APM的边AP上任取两点B,C,过B作AM的平行线交PM于N,过N作MC的平行线交AP于D.若=,则的值为( )
A. B. C.2 D.3
5.如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE OP;③S△AOD=S四边形OECF;其中正确结论的个数( )
A.1 B.3 C.2 D.0
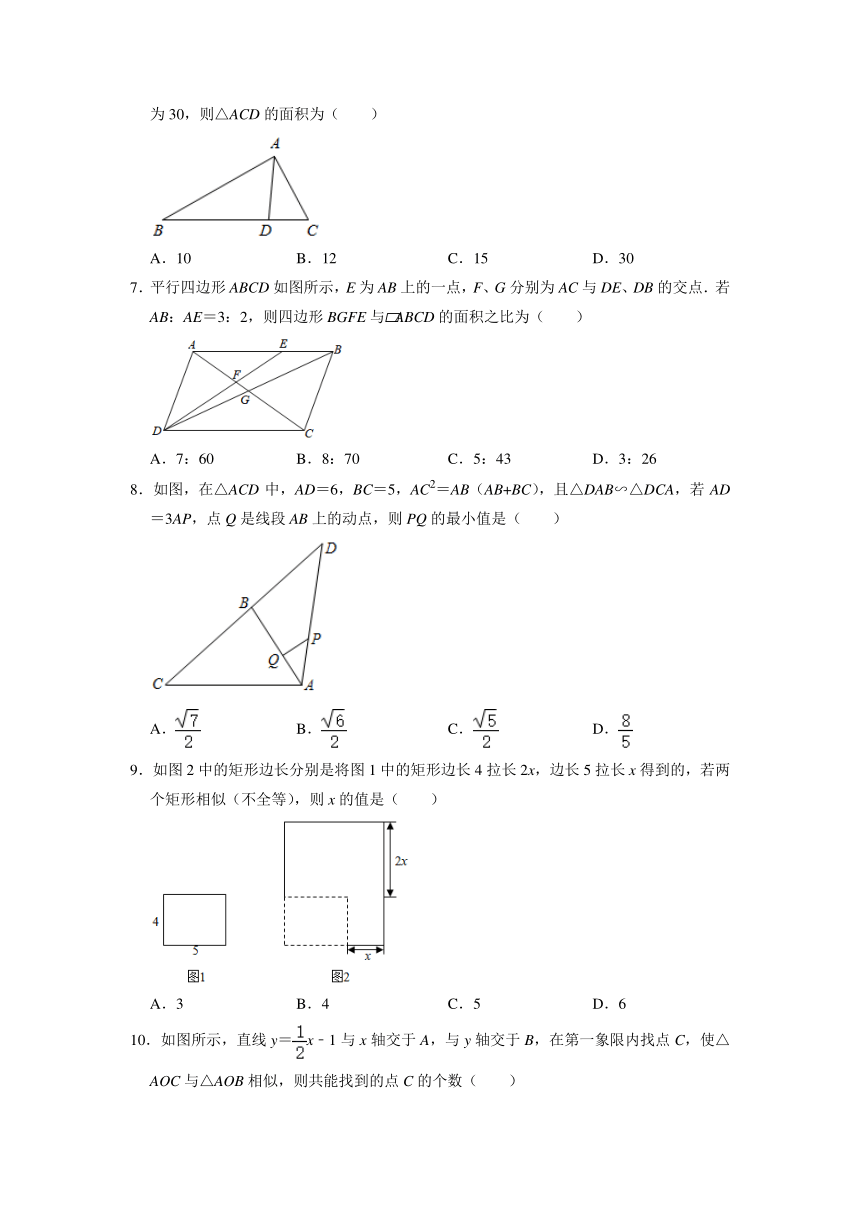
6.如图,点D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.若△ABD的面积为30,则△ACD的面积为( )
A.10 B.12 C.15 D.30
7.平行四边形ABCD如图所示,E为AB上的一点,F、G分别为AC与DE、DB的交点.若AB:AE=3:2,则四边形BGFE与 ABCD的面积之比为( )
A.7:60 B.8:70 C.5:43 D.3:26
8.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,点Q是线段AB上的动点,则PQ的最小值是( )
A. B. C. D.
9.如图2中的矩形边长分别是将图1中的矩形边长4拉长2x,边长5拉长x得到的,若两个矩形相似(不全等),则x的值是( )
A.3 B.4 C.5 D.6
10.如图所示,直线y=x﹣1与x轴交于A,与y轴交于B,在第一象限内找点C,使△AOC与△AOB相似,则共能找到的点C的个数( )
A.1 B.2 C.3 D.4
二.填空题(共10小题,满分30分)
11.已知==≠0,则= .
12.若===k成立,则k的值为 .
13.如图:l1∥l2∥l3,AB=6,BC=4,CD=2,CF=3,则EG= .
14.如图,矩形ABCD中,AB=6,BC=8,对角线BD的垂直平分线EF交AD于点E、交BC于点F,则线段EF的长为 .
15.如图,△A′B′C′与△ABC是位似图形,点O为位似中心,若OA′=A′A,则△A′B′C′与△ABC的面积比为 .
16.如图,在菱形ABCD中,已知∠ABC=60°,直线EF过点D,且与BA、BC的延长线分别交于点E、F,M是CE与AF的交点.若CM=4,EM=5,则AC= .
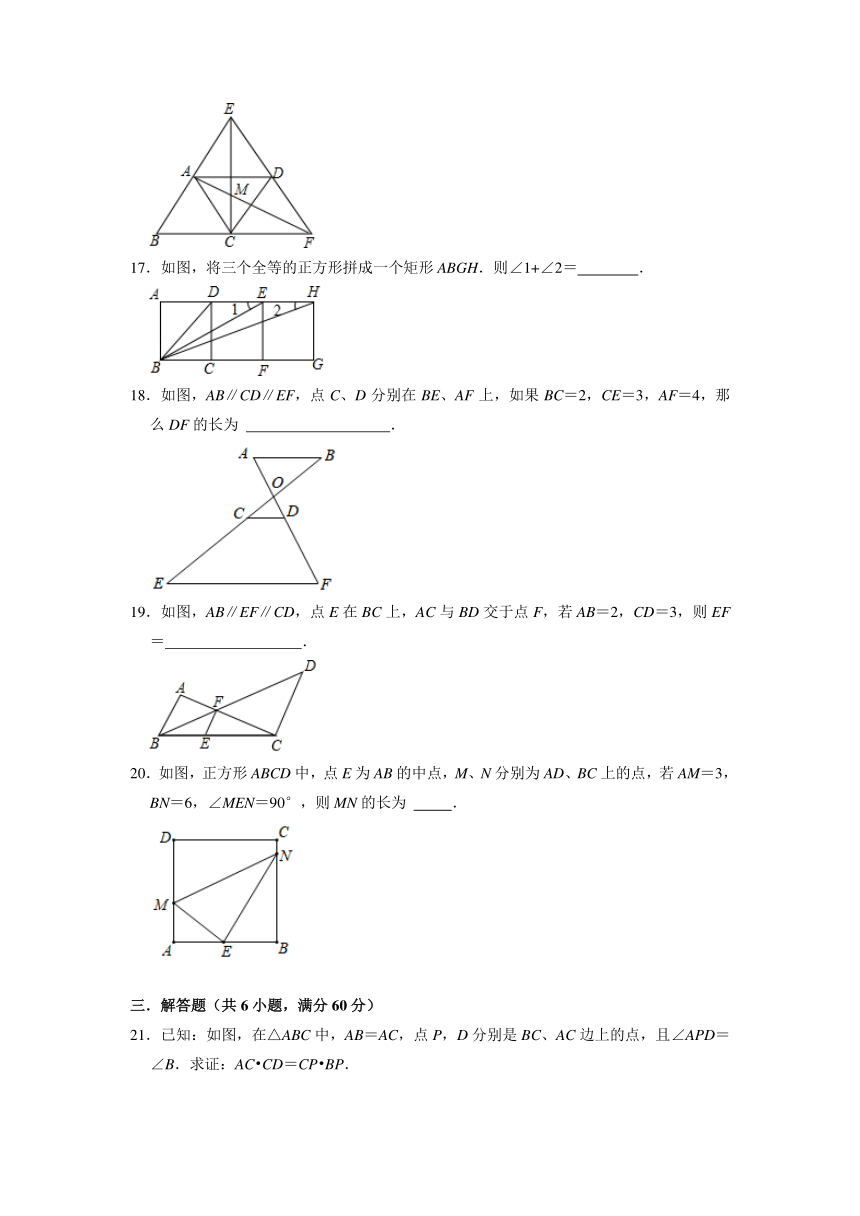
17.如图,将三个全等的正方形拼成一个矩形ABGH.则∠1+∠2= .
18.如图,AB∥CD∥EF,点C、D分别在BE、AF上,如果BC=2,CE=3,AF=4,那么DF的长为 .
19.如图,AB∥EF∥CD,点E在BC上,AC与BD交于点F,若AB=2,CD=3,则EF= .
20.如图,正方形ABCD中,点E为AB的中点,M、N分别为AD、BC上的点,若AM=3,BN=6,∠MEN=90°,则MN的长为 .
三.解答题(共6小题,满分60分)
21.已知:如图,在△ABC中,AB=AC,点P,D分别是BC、AC边上的点,且∠APD=∠B.求证:AC CD=CP BP.
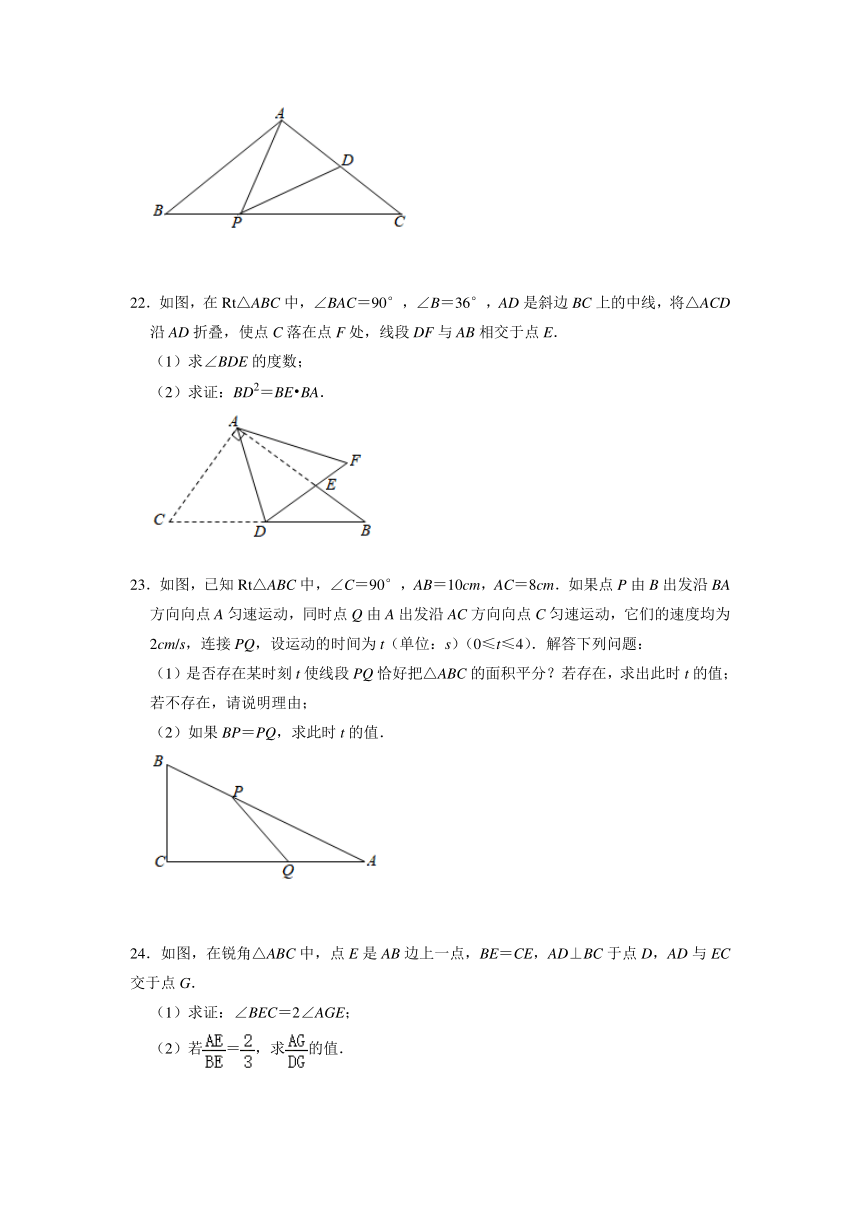
22.如图,在Rt△ABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将△ACD沿AD折叠,使点C落在点F处,线段DF与AB相交于点E.
(1)求∠BDE的度数;
(2)求证:BD2=BE BA.
23.如图,已知Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)是否存在某时刻t使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由;
(2)如果BP=PQ,求此时t的值.
24.如图,在锐角△ABC中,点E是AB边上一点,BE=CE,AD⊥BC于点D,AD与EC交于点G.
(1)求证:∠BEC=2∠AGE;
(2)若=,求的值.
25.如图1,在正方形ABCD中,E为BC延长线上一点,且BC=3CE,F为CD的中点,EF的延长线交AD于点G,连接BG.
(1)求的值;
(2)求证:BG=EG;
(3)如图2,M为AB的中点,DM交BG于点N,连接CN,求证:CN∥GE.
26.如图,在矩形ABCD中,BC=2AB=4,点G为边BC上一点,过点G作GE⊥AG,且GE=2AG,GE交DC于点F,连接AE.
(1)求证:△ABG∽△GCF;
(2)连接CE,求证:∠DCE=∠AEG;
(3)当点E正好在BD的延长线上时,求BG的长.
参考答案
一.选择题(共10小题,满分30分)
1.解:A.∵,∴4x=3y,正确,不符合题意;
B.∵,∴,错误,符合题意;
C.∵,∴,正确,不符合题意;
D.∵,∴,正确,不符合题意;
故选:B.
2.解:A.4×10≠6×5,故不符合题意,
B.1×4≠2×3,故不符合题意,
C.,故不符合题意,
D.,故符合题意,
故选:D.
3.解:∵AB=3,AC=8,
∴BC=AC﹣AB=8﹣3=5,
∵直线l1∥l2∥l3,
∴=,
∴=,
故选:C.
4.解:∵BN∥AM,=,
∴=,
∵DN∥CM,
∴==,
故选:B.
5.解:∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中,
,
∴△DAP≌△ABQ(SAS),
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP,故结论①正确;
∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴=,
∴AO2=OD OP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OE OP;故结论②错误;
在△CQF与△BPE中,
,
∴△CQF≌△BPE(ASA),
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(SAS),
∴S△ADF=S△DCE,
∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,
即S△AOD=S四边形OECF;故结论③正确;
故选:C.
6.解:∵∠DAC=∠B,∠C=∠C,
∴△ACD∽△BCA,
∵AB=4,AD=2,
∴==,
∴△ACD的面积=10,
故选:A.
7.解:∵AB:AE=3:2,
∴BE:AB=1:3,
∴S△DBE=S△ABD=S ABCD,
∵四边形ABCD是平行四边形,
∴AB∥CD,AG=GC,
∴△AEF∽△CDF,
∴,
∴设AF=2a,CF=3a,
∴AC=5a,
∴AG=CG=a,
∴FG=a,
∴AG=5FG,
∴S△DFG=S△ADG=S ABCD,
∴S四边形BGFE=S△DBE﹣S△DFG=S ABCD,
∴四边形BGFE与 ABCD的面积之比为7:60,
故选:A.
8.解:∵△DAB∽△DCA,
∴=,
∴=,
解得:BD=4(负值舍去),
∵△DAB∽△DCA,
∴,
∴AC=,
∵AC2=AB(AB+BC),
∴(AB)2=AB(AB+BC),
∴AB=4,
∴AB=BD=4,
过B作BH⊥AD于H,
∴AH=AD=3,
∴BH===,
∵AD=3AP,AD=6,
∴AP=2,
当PQ⊥AB时,PQ的值最小,
∵∠AQP=∠AHB=90°,∠PAQ=∠BAH,
∴△APQ∽△ABH,
∴,
∴=,
∴PQ=,
故选:A.
9.解:由题意,两个矩形相似,
∴=或=,
解得x=3或0(0不符合题意舍弃),
故选:A.
10.解:∵点C在第一象限,
∴当点C为直角顶点时,有两种情形,
当点A为直角顶点时,也有两种情形,共有4种情形.
故选:D.
二.填空题(共10小题,满分30分)
11.解:设===k(k≠0),
则,
解得:a=﹣k.b=k,c=k,
所以
=
=,
故答案为:.
12.解:当a+b+c≠0时,根据比例的等比性质,得k==1:
当a+b+c=0时,即a+b=﹣c,则k==﹣2.
故答案为:1或﹣2.
13.解:∵l1∥l2∥l3,
∴即,
∴CG=1.5,FG=3+1.5=4.5,
∵,即,
解得x=9.
∴EG=9.
故答案为:9.
14.解:∵四边形ABCD是矩形,
∴∠A=90°,又AB=6,AD=BC=8,
∴BD==10,
∵EF是BD的垂直平分线,
∴OB=OD=5,∠BOF=90°,又∠C=90°,
∴△BOF∽△BCD,
∴=,
∴=,
解得,OF=,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠EDO=∠FBO,
∵EF是BD的垂直平分线,
∴BO=DO,EF⊥BD,
在△DEO和△BFO中,
,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∴EF=2OF=.
故答案为:.
15.解:∵OA′=A′A,
∴=,
∵△A′B′C′与△ABC是位似图形,
∴△A′B′C′∽△ABC,
∴△A′B′C′与△ABC的面积比=()2=,
故答案为:1:4.
16.解:在菱形ABCD中,AD∥BC,AB∥DC,
∴△EAD∽△EBF.△FDC∽△EBF,
∴△EAD∽△FDC,
∴=,
∵∠ABC=∠ADC=60°,
∴△ABC和△ADC是等边三角形,
∴AD=AC=DC,
∴=,
∵∠EAC=∠ACF=120°,
∴△EAC∽△ACF,
∴∠AEC=∠CAF,
∵∠ACM=∠ECA,
∴△ACM∽△ECA,
∴=,
∴AC2=CE CM=9×4=36,
∴AC=6(负值舍去).
故答案为:6.
17.解:设边长为a的三个正方形拼成一个矩形ABGH,
∴BD==a,
∵DE=a,DH=2a,
∴=,
∵∠BDH=∠HDB,
∴△BDE∽△HDB,
∴∠2=∠DBE,
∵∠ADB=∠1+∠DBE=45°,
∴∠1+∠2=45°.
故答案为:45°.
18.解:∵AB∥CD∥EF,
∴=,
∴=,
∴DF=,
故答案为:.
19.解:∵AB∥EF,
∴△CEF∽△CBA,
∴=,
同理可得:=,
∴+=+=1,
∴+=1,
解得:EF=,
故答案为:.
20.解:∵点E为AB的中点,
∴AE=BE,
∵∠MEN=90°,
∴∠AEM+∠BEN=90°=∠AEM+∠AME,
∴∠AME=∠BEN,
又∵∠A=∠B=90°,
∴△AEM∽△BNE,
∴,
∴AE BE=AM BN=18,
∴AE=BE=3,
∴ME2=AM2+AE2=27,EN2=BE2+BN2=54,
∴MN===9,
故答案为:9.
三.解答题(共6小题,满分60分)
21.证明:∵AB=AC,
∴∠B=∠C.
∵∠APD=∠B,
∴∠APD=∠B=∠C.
∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴=,
∴AB CD=CP BP.
∵AB=AC,
∴AC CD=CP BP.
22.解:(1)∵∠BAC=90°,∠B=36°,
∴∠C=54°,
又∵AD是中线,
∴CD=AD=BD,
∴∠C=∠CAD=54°,
∴∠ADC=72°,
由折叠性质可得,
∠ADC=∠ADF=72°,
∴∠BDE=36°;
(2)∵∠CAD=54°,∠CAB=90°,
∴∠DAB=36°=∠BDE,
又∵∠B=∠B,
∴△ADB∽△DEB,
∴,
∴BD2=BE BA.
23.解:(1)不存在某时刻t,使线段PQ恰好把△ABC的面积平分,理由如下:
如图,过点P作PD⊥AC于点D,
∴PD∥BC,
在Rt△ABC中,∠C=90°,
∵AB=10cm,AC=8cm.
∴BC=6cm,
假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则有S△APQ=S△ABC,
∵S△ABC=AC BC=8×6=24(cm2),
∴S△APQ=12(cm2),
∵PD∥BC,
∴=,
∴=,
∴PD=,
∴S△APQ=2t×=﹣t2+6t,
∴﹣t2+6t=12,
化简得t2﹣5t+10=0,
∵△=(﹣5)2﹣4×1×10=﹣15<0,
∴此方程无实数根,
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分;
(2)∵PD∥BC,
∴=,
∴=,
∴AD=,
∵PD=,PQ=BP=2t,
∴QD=AD﹣AQ=﹣2t=,
在Rt△PQD中,根据勾股定理,得
QD2+PD2=PQ2,
∴()2+()2=(2t)2,
化简,得13t2﹣90t+125=0,
解得t1=5,t2=,
∵t=5>4,不符合题意,舍去,
∴t=s.
24.(1)证明:∵∠AGE=∠CGD,AD⊥BC,即∠GDC=90°,
∴∠ECB=90°﹣∠CGD=90°﹣∠AGE,
∵BE=CE,
∴∠B=∠ECB=90°﹣∠CGD=90°﹣∠AGE,
∴∠BEC=180°﹣∠B﹣∠ECB=180°﹣2(90°﹣∠AGE)=2∠AGE,
∴∠BEC=2∠AGE;
(2)如图,过点E作EF⊥BC交于点F,
由(1)知∠BEC=2∠AGE,则∠BEC=∠AGE+∠EAG,
∴∠AGE=∠EAG,则AE=EG,
∵∠EFC=∠GDC,∠FCE=∠DCG,
∴△EFC∽△GDC,
∵,BE=BC,
∴,,
∵,
∴,
∵∠ABC=∠EBC,∠EFB=∠ADB=90°,
∴△BEF∽△BAD,
∴,
∵,
∴,
∵AD=,GD=EF,
∴AG=EF,
∴=4.
25.解:(1)∵F为CD的中点,
∴DF=CF,
∵四边形ABCD为正方形,
∴AD∥BC,
∴∠GDF=∠ECF=90°.
又∵∠DFG=∠CFE.
∴△GDF≌△ECF(ASA),
∴DG=CE.
∵BC=3CE,
∴CE=BC=DG,
∴AG=AD﹣DG=BC﹣CE=BC﹣BC=BC,
∴==2;
(2)过点G作GH⊥BC于H,
∴CH=DG=CE=BC,
∴EH=CH+CE=BC,
在△ABG和△HGE中,
,
∴△ABG≌△HGE(SAS),
∴BG=EG;
(3)过点M作MT∥AD交BG于T,
∵M为AB的中点,
∴MT=AG=DG,
∵AD∥MT,
∴∠NMT=∠NDG,
在△MNT和△DNG中,
,
∴△MNT≌△DNG(AAS),
∴NT=NG,
∴BG=4NG,
∴=,
∵BC=3CE,
∴=,
∴=,
∵∠CBN=∠EBG,
∴△CBN∽△EBG,
∴∠BCN=∠BEG,
∴CN∥EG.
26.解:(1)∵四边形ABCD为矩形,
∴∠B=∠D=90°,
∵GE⊥AG,
∴∠AGB+∠CGF=90°,
∴∠BAG+∠AGB=90°,
∴∠BAG=∠CGF,
∴△ABG∽△GCF;
(2)如图所示,连接AC,交GE于M点,
∵GE=2AG,BC=2AB,
∴=,
又∵∠AGE=∠B=90°,
∴△AGE∽△ABC,
∴∠AEG=∠ACB,
∵∠AME=∠GMC,
∴△AME∽△GMC,
∴=,
又∵∠AMG=∠EMC,
∴△AMG∽△EMC,
∴∠AGM=∠ECM=90°,
即:∠BCD=∠ECM=90°,
∴∠ACB=∠DCE,
∴∠AEG=∠DCE;
(3)如图,作EH⊥BC的延长线于H点,设BG=x,
∵△ABG∽△GHE,GE=2AG,
∴EH=2BG=2x,GH=2AB=4,
则BH=BG+GH=4+x,
∵△DCB∽△EHB,
∴==,
∴=,
解得:x=,
经检验,x=是原分式方程的解,
∴BG的长为.
一.选择题(共10小题,满分30分)
1.已知,那么下列等式中不成立的是( )
A.4x=3y B. C. D.
2.下列各组的四条线段a,b,c,d是成比例线段的是( )
A.a=4,b=6,c=5,d=10 B.a=1,b=2,c=3,d=4
C.,b=3,c=2, D.a=2,,,
3.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.且AB=3,AC=8,则的值为( )
A. B. C. D.
4.如图,在△APM的边AP上任取两点B,C,过B作AM的平行线交PM于N,过N作MC的平行线交AP于D.若=,则的值为( )
A. B. C.2 D.3
5.如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE OP;③S△AOD=S四边形OECF;其中正确结论的个数( )
A.1 B.3 C.2 D.0
6.如图,点D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.若△ABD的面积为30,则△ACD的面积为( )
A.10 B.12 C.15 D.30
7.平行四边形ABCD如图所示,E为AB上的一点,F、G分别为AC与DE、DB的交点.若AB:AE=3:2,则四边形BGFE与 ABCD的面积之比为( )
A.7:60 B.8:70 C.5:43 D.3:26
8.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,点Q是线段AB上的动点,则PQ的最小值是( )
A. B. C. D.
9.如图2中的矩形边长分别是将图1中的矩形边长4拉长2x,边长5拉长x得到的,若两个矩形相似(不全等),则x的值是( )
A.3 B.4 C.5 D.6
10.如图所示,直线y=x﹣1与x轴交于A,与y轴交于B,在第一象限内找点C,使△AOC与△AOB相似,则共能找到的点C的个数( )
A.1 B.2 C.3 D.4
二.填空题(共10小题,满分30分)
11.已知==≠0,则= .
12.若===k成立,则k的值为 .
13.如图:l1∥l2∥l3,AB=6,BC=4,CD=2,CF=3,则EG= .
14.如图,矩形ABCD中,AB=6,BC=8,对角线BD的垂直平分线EF交AD于点E、交BC于点F,则线段EF的长为 .
15.如图,△A′B′C′与△ABC是位似图形,点O为位似中心,若OA′=A′A,则△A′B′C′与△ABC的面积比为 .
16.如图,在菱形ABCD中,已知∠ABC=60°,直线EF过点D,且与BA、BC的延长线分别交于点E、F,M是CE与AF的交点.若CM=4,EM=5,则AC= .
17.如图,将三个全等的正方形拼成一个矩形ABGH.则∠1+∠2= .
18.如图,AB∥CD∥EF,点C、D分别在BE、AF上,如果BC=2,CE=3,AF=4,那么DF的长为 .
19.如图,AB∥EF∥CD,点E在BC上,AC与BD交于点F,若AB=2,CD=3,则EF= .
20.如图,正方形ABCD中,点E为AB的中点,M、N分别为AD、BC上的点,若AM=3,BN=6,∠MEN=90°,则MN的长为 .
三.解答题(共6小题,满分60分)
21.已知:如图,在△ABC中,AB=AC,点P,D分别是BC、AC边上的点,且∠APD=∠B.求证:AC CD=CP BP.
22.如图,在Rt△ABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将△ACD沿AD折叠,使点C落在点F处,线段DF与AB相交于点E.
(1)求∠BDE的度数;
(2)求证:BD2=BE BA.
23.如图,已知Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)是否存在某时刻t使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由;
(2)如果BP=PQ,求此时t的值.
24.如图,在锐角△ABC中,点E是AB边上一点,BE=CE,AD⊥BC于点D,AD与EC交于点G.
(1)求证:∠BEC=2∠AGE;
(2)若=,求的值.
25.如图1,在正方形ABCD中,E为BC延长线上一点,且BC=3CE,F为CD的中点,EF的延长线交AD于点G,连接BG.
(1)求的值;
(2)求证:BG=EG;
(3)如图2,M为AB的中点,DM交BG于点N,连接CN,求证:CN∥GE.
26.如图,在矩形ABCD中,BC=2AB=4,点G为边BC上一点,过点G作GE⊥AG,且GE=2AG,GE交DC于点F,连接AE.
(1)求证:△ABG∽△GCF;
(2)连接CE,求证:∠DCE=∠AEG;
(3)当点E正好在BD的延长线上时,求BG的长.
参考答案
一.选择题(共10小题,满分30分)
1.解:A.∵,∴4x=3y,正确,不符合题意;
B.∵,∴,错误,符合题意;
C.∵,∴,正确,不符合题意;
D.∵,∴,正确,不符合题意;
故选:B.
2.解:A.4×10≠6×5,故不符合题意,
B.1×4≠2×3,故不符合题意,
C.,故不符合题意,
D.,故符合题意,
故选:D.
3.解:∵AB=3,AC=8,
∴BC=AC﹣AB=8﹣3=5,
∵直线l1∥l2∥l3,
∴=,
∴=,
故选:C.
4.解:∵BN∥AM,=,
∴=,
∵DN∥CM,
∴==,
故选:B.
5.解:∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中,
,
∴△DAP≌△ABQ(SAS),
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP,故结论①正确;
∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴=,
∴AO2=OD OP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OE OP;故结论②错误;
在△CQF与△BPE中,
,
∴△CQF≌△BPE(ASA),
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(SAS),
∴S△ADF=S△DCE,
∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,
即S△AOD=S四边形OECF;故结论③正确;
故选:C.
6.解:∵∠DAC=∠B,∠C=∠C,
∴△ACD∽△BCA,
∵AB=4,AD=2,
∴==,
∴△ACD的面积=10,
故选:A.
7.解:∵AB:AE=3:2,
∴BE:AB=1:3,
∴S△DBE=S△ABD=S ABCD,
∵四边形ABCD是平行四边形,
∴AB∥CD,AG=GC,
∴△AEF∽△CDF,
∴,
∴设AF=2a,CF=3a,
∴AC=5a,
∴AG=CG=a,
∴FG=a,
∴AG=5FG,
∴S△DFG=S△ADG=S ABCD,
∴S四边形BGFE=S△DBE﹣S△DFG=S ABCD,
∴四边形BGFE与 ABCD的面积之比为7:60,
故选:A.
8.解:∵△DAB∽△DCA,
∴=,
∴=,
解得:BD=4(负值舍去),
∵△DAB∽△DCA,
∴,
∴AC=,
∵AC2=AB(AB+BC),
∴(AB)2=AB(AB+BC),
∴AB=4,
∴AB=BD=4,
过B作BH⊥AD于H,
∴AH=AD=3,
∴BH===,
∵AD=3AP,AD=6,
∴AP=2,
当PQ⊥AB时,PQ的值最小,
∵∠AQP=∠AHB=90°,∠PAQ=∠BAH,
∴△APQ∽△ABH,
∴,
∴=,
∴PQ=,
故选:A.
9.解:由题意,两个矩形相似,
∴=或=,
解得x=3或0(0不符合题意舍弃),
故选:A.
10.解:∵点C在第一象限,
∴当点C为直角顶点时,有两种情形,
当点A为直角顶点时,也有两种情形,共有4种情形.
故选:D.
二.填空题(共10小题,满分30分)
11.解:设===k(k≠0),
则,
解得:a=﹣k.b=k,c=k,
所以
=
=,
故答案为:.
12.解:当a+b+c≠0时,根据比例的等比性质,得k==1:
当a+b+c=0时,即a+b=﹣c,则k==﹣2.
故答案为:1或﹣2.
13.解:∵l1∥l2∥l3,
∴即,
∴CG=1.5,FG=3+1.5=4.5,
∵,即,
解得x=9.
∴EG=9.
故答案为:9.
14.解:∵四边形ABCD是矩形,
∴∠A=90°,又AB=6,AD=BC=8,
∴BD==10,
∵EF是BD的垂直平分线,
∴OB=OD=5,∠BOF=90°,又∠C=90°,
∴△BOF∽△BCD,
∴=,
∴=,
解得,OF=,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠EDO=∠FBO,
∵EF是BD的垂直平分线,
∴BO=DO,EF⊥BD,
在△DEO和△BFO中,
,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∴EF=2OF=.
故答案为:.
15.解:∵OA′=A′A,
∴=,
∵△A′B′C′与△ABC是位似图形,
∴△A′B′C′∽△ABC,
∴△A′B′C′与△ABC的面积比=()2=,
故答案为:1:4.
16.解:在菱形ABCD中,AD∥BC,AB∥DC,
∴△EAD∽△EBF.△FDC∽△EBF,
∴△EAD∽△FDC,
∴=,
∵∠ABC=∠ADC=60°,
∴△ABC和△ADC是等边三角形,
∴AD=AC=DC,
∴=,
∵∠EAC=∠ACF=120°,
∴△EAC∽△ACF,
∴∠AEC=∠CAF,
∵∠ACM=∠ECA,
∴△ACM∽△ECA,
∴=,
∴AC2=CE CM=9×4=36,
∴AC=6(负值舍去).
故答案为:6.
17.解:设边长为a的三个正方形拼成一个矩形ABGH,
∴BD==a,
∵DE=a,DH=2a,
∴=,
∵∠BDH=∠HDB,
∴△BDE∽△HDB,
∴∠2=∠DBE,
∵∠ADB=∠1+∠DBE=45°,
∴∠1+∠2=45°.
故答案为:45°.
18.解:∵AB∥CD∥EF,
∴=,
∴=,
∴DF=,
故答案为:.
19.解:∵AB∥EF,
∴△CEF∽△CBA,
∴=,
同理可得:=,
∴+=+=1,
∴+=1,
解得:EF=,
故答案为:.
20.解:∵点E为AB的中点,
∴AE=BE,
∵∠MEN=90°,
∴∠AEM+∠BEN=90°=∠AEM+∠AME,
∴∠AME=∠BEN,
又∵∠A=∠B=90°,
∴△AEM∽△BNE,
∴,
∴AE BE=AM BN=18,
∴AE=BE=3,
∴ME2=AM2+AE2=27,EN2=BE2+BN2=54,
∴MN===9,
故答案为:9.
三.解答题(共6小题,满分60分)
21.证明:∵AB=AC,
∴∠B=∠C.
∵∠APD=∠B,
∴∠APD=∠B=∠C.
∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴=,
∴AB CD=CP BP.
∵AB=AC,
∴AC CD=CP BP.
22.解:(1)∵∠BAC=90°,∠B=36°,
∴∠C=54°,
又∵AD是中线,
∴CD=AD=BD,
∴∠C=∠CAD=54°,
∴∠ADC=72°,
由折叠性质可得,
∠ADC=∠ADF=72°,
∴∠BDE=36°;
(2)∵∠CAD=54°,∠CAB=90°,
∴∠DAB=36°=∠BDE,
又∵∠B=∠B,
∴△ADB∽△DEB,
∴,
∴BD2=BE BA.
23.解:(1)不存在某时刻t,使线段PQ恰好把△ABC的面积平分,理由如下:
如图,过点P作PD⊥AC于点D,
∴PD∥BC,
在Rt△ABC中,∠C=90°,
∵AB=10cm,AC=8cm.
∴BC=6cm,
假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则有S△APQ=S△ABC,
∵S△ABC=AC BC=8×6=24(cm2),
∴S△APQ=12(cm2),
∵PD∥BC,
∴=,
∴=,
∴PD=,
∴S△APQ=2t×=﹣t2+6t,
∴﹣t2+6t=12,
化简得t2﹣5t+10=0,
∵△=(﹣5)2﹣4×1×10=﹣15<0,
∴此方程无实数根,
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分;
(2)∵PD∥BC,
∴=,
∴=,
∴AD=,
∵PD=,PQ=BP=2t,
∴QD=AD﹣AQ=﹣2t=,
在Rt△PQD中,根据勾股定理,得
QD2+PD2=PQ2,
∴()2+()2=(2t)2,
化简,得13t2﹣90t+125=0,
解得t1=5,t2=,
∵t=5>4,不符合题意,舍去,
∴t=s.
24.(1)证明:∵∠AGE=∠CGD,AD⊥BC,即∠GDC=90°,
∴∠ECB=90°﹣∠CGD=90°﹣∠AGE,
∵BE=CE,
∴∠B=∠ECB=90°﹣∠CGD=90°﹣∠AGE,
∴∠BEC=180°﹣∠B﹣∠ECB=180°﹣2(90°﹣∠AGE)=2∠AGE,
∴∠BEC=2∠AGE;
(2)如图,过点E作EF⊥BC交于点F,
由(1)知∠BEC=2∠AGE,则∠BEC=∠AGE+∠EAG,
∴∠AGE=∠EAG,则AE=EG,
∵∠EFC=∠GDC,∠FCE=∠DCG,
∴△EFC∽△GDC,
∵,BE=BC,
∴,,
∵,
∴,
∵∠ABC=∠EBC,∠EFB=∠ADB=90°,
∴△BEF∽△BAD,
∴,
∵,
∴,
∵AD=,GD=EF,
∴AG=EF,
∴=4.
25.解:(1)∵F为CD的中点,
∴DF=CF,
∵四边形ABCD为正方形,
∴AD∥BC,
∴∠GDF=∠ECF=90°.
又∵∠DFG=∠CFE.
∴△GDF≌△ECF(ASA),
∴DG=CE.
∵BC=3CE,
∴CE=BC=DG,
∴AG=AD﹣DG=BC﹣CE=BC﹣BC=BC,
∴==2;
(2)过点G作GH⊥BC于H,
∴CH=DG=CE=BC,
∴EH=CH+CE=BC,
在△ABG和△HGE中,
,
∴△ABG≌△HGE(SAS),
∴BG=EG;
(3)过点M作MT∥AD交BG于T,
∵M为AB的中点,
∴MT=AG=DG,
∵AD∥MT,
∴∠NMT=∠NDG,
在△MNT和△DNG中,
,
∴△MNT≌△DNG(AAS),
∴NT=NG,
∴BG=4NG,
∴=,
∵BC=3CE,
∴=,
∴=,
∵∠CBN=∠EBG,
∴△CBN∽△EBG,
∴∠BCN=∠BEG,
∴CN∥EG.
26.解:(1)∵四边形ABCD为矩形,
∴∠B=∠D=90°,
∵GE⊥AG,
∴∠AGB+∠CGF=90°,
∴∠BAG+∠AGB=90°,
∴∠BAG=∠CGF,
∴△ABG∽△GCF;
(2)如图所示,连接AC,交GE于M点,
∵GE=2AG,BC=2AB,
∴=,
又∵∠AGE=∠B=90°,
∴△AGE∽△ABC,
∴∠AEG=∠ACB,
∵∠AME=∠GMC,
∴△AME∽△GMC,
∴=,
又∵∠AMG=∠EMC,
∴△AMG∽△EMC,
∴∠AGM=∠ECM=90°,
即:∠BCD=∠ECM=90°,
∴∠ACB=∠DCE,
∴∠AEG=∠DCE;
(3)如图,作EH⊥BC的延长线于H点,设BG=x,
∵△ABG∽△GHE,GE=2AG,
∴EH=2BG=2x,GH=2AB=4,
则BH=BG+GH=4+x,
∵△DCB∽△EHB,
∴==,
∴=,
解得:x=,
经检验,x=是原分式方程的解,
∴BG的长为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
