北师大版高中数学必修1《对数函数》参考课件1(共24张PPT)
文档属性
| 名称 | 北师大版高中数学必修1《对数函数》参考课件1(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 872.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 20:40:42 | ||
图片预览






文档简介
(共24张PPT)
a>1
0图
象
性
质
1.定义域:R
2.值域:(0,+∞)
3.过定点(0,1),即x=0时,y=1
4. 当x>0时, y>1;
当x<0时,0当x>0时,0当x<0时,y>1;
5.在 R上是增函数
在R上是减函数
回顾指数函数图象及性质
现在有一张纸,我把这张纸对折一次就变成了两层;我对折两次纸就变成了四层;如果我们设把纸对折的次数为x,对折后纸的层数为y,那么,试建立y关于x的函数关系式。
你能写出这个X关于Y的函数的关系表达式吗
解:
2次
3次
提问:如果我发现对折后的纸有4层,那么我对折了多少次?
如果我发现对折后的纸有8层,那么我对折了多少次?
… … 16层呢,32层呢 … …
我们可以发现:x关于y也可以建立一个函数。
指数式化对数式
这个就是我们要的函数关系
交换X和Y,以符合习惯
一般地,函数
就叫做对数函数。x为它的自变
对数函数的定义
以上两个函数也是对数函数!
量,函数的定义域为
提问:
我们知道,函数
和
互为反函数。
函数
和
是什么关系呢?
函数
和
互为反函数!
2.利用对称性画图.
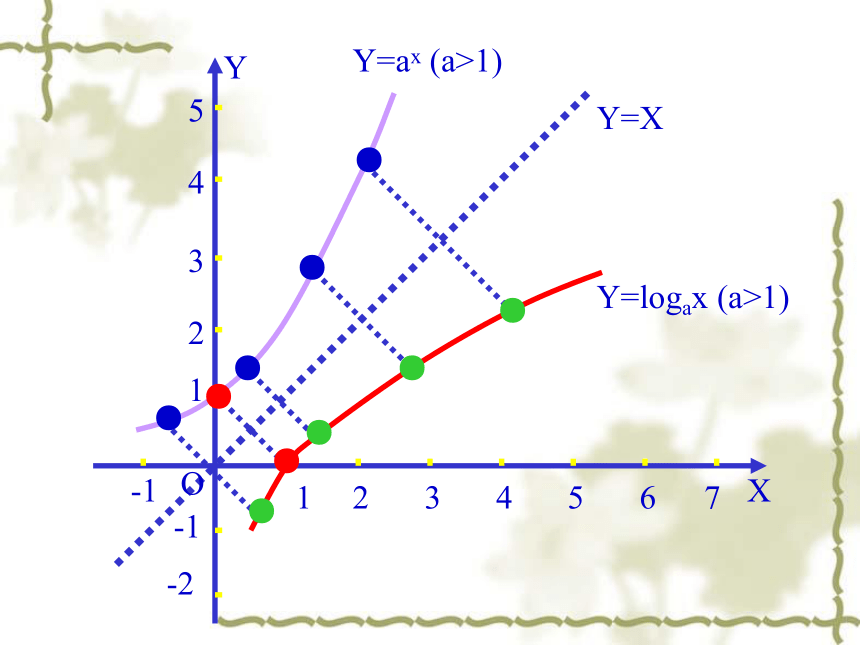
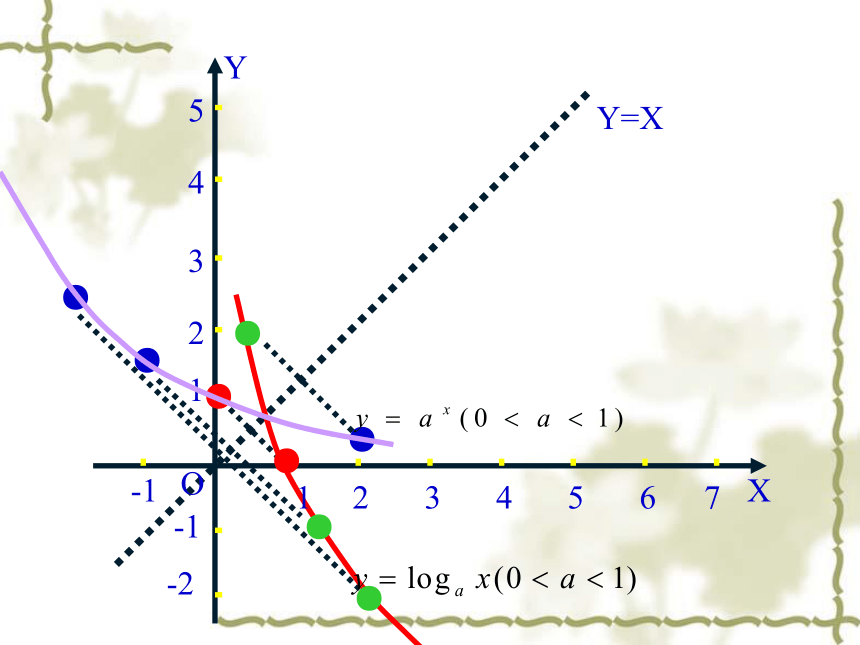
因为指数函数y=ax (0与对数函数y=logax(0象关于直线y=x对称.
X
Y=ax (a>1)
Y
O
1
1
2
2
3
3
4
4
5
5
6
7
Y=logax (a>1)
Y=X
-1
-1
-2
●
●
●
●
●
●
●
●
●
●
X
Y
O
1
1
2
2
3
3
4
4
5
5
6
7
Y=X
-1
-1
-2
●
●
●
●
●
●
●
●
1
1
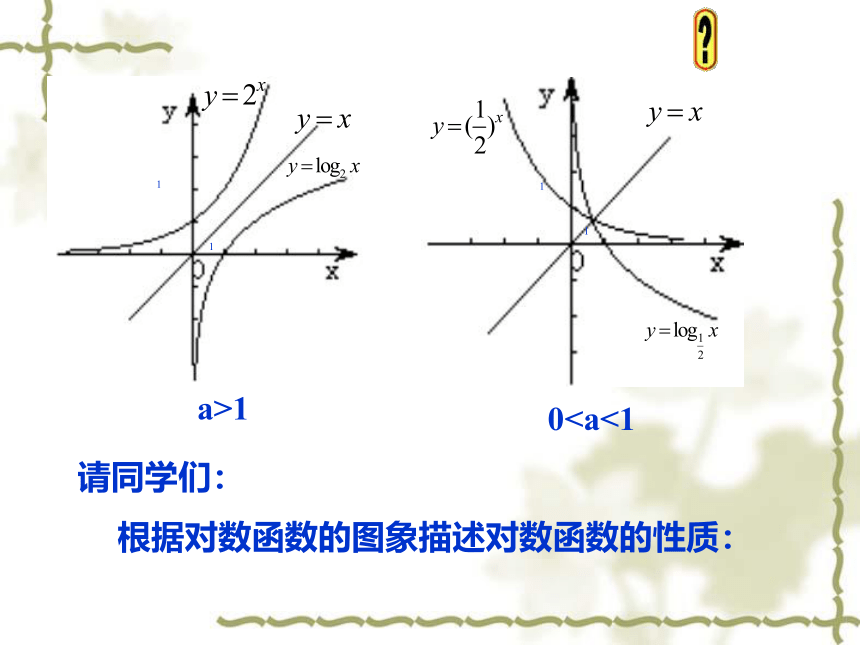
a>1
1
1
0请同学们:
根据对数函数的图象描述对数函数的性质:
图像的特征 函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占满了整个y轴;
值域: R
3. 过(1.0)点
当x=1时,y=0。
增函数
4. 单调性:
a>1时,图像上升;
5. 函数值分布:
a>1:
当:x>1时, 图像在y轴上方;
当0a>1:
当0当x>1, 则 y>0,
图像的特征 函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占满了整个y轴;
值域: R
3. 过(1.0)点
当x=1时,y=0。
4. 单调性:
0减函数
5. 函数值分布:
当 00当:x>1, 图像在y轴下方;
当:x>1, 则y<0
当:00;
0当 05. 函数值分布:
值域: R
当x=1时,y=0。
当:x>1时, 图像在y轴上方;
图像的特征 函数性质
2. 图像在y轴的投影占
满了整个y轴;
1.图像位于y轴右侧;
定义域:x>0
3. 过(1.0)点
4. 单调性:
增函数
0减函数
a>1时,图像上升;
0当:x>1, 图像在y轴下方;
当:x>1, 则y<0
当00;
a>1:
当0a>1:
当00当x>1, 则 y>0,
特殊点:
图
象
性
质
定义域:
值域:
单调性:
增函数
减函数
函 数值
的
分 布
当x>1, 则y>0;
当0当x>1, 则y<0;
当00:
对数函数图像及性质
名 称 指数函数 对数函数
一般形式
定义域
值域
单调性 a>1, 增函数
01, 增函数
0函数值
变
化情况 a>1: x>0, y>1
x<0, 000, 0x<0, y>1 a>1: x>1, y>0
001, y<0
00
图像关系 的图像于 的图像关于直线y=x对称
指数函数与对数函数对比
指数函数
对数函数
按要求回答问题
(1) y=log3 (x- 2)
(1)以上函数的定义域。
(2) y=log2(x2 +1)
(2)以上函数如果底数为
a(a>0且a ≠1)时,函数必过那一点。
例二:判断下列各组数中两个值的大小:
(1) log30.8,
log33.7
(3) loga5.9,
loga3.1
log0.52.9
(2) log0.54.2,
(01. 对数函数是指数函数的反函数,对数函数的定义域、值域分别为相应的指数函数的值域和定义域,它们的图象关于 成轴对称.
2. 当a>1, 在 为增函数.
当0课堂小结:
作业:略
(2)y=log3 (-x)
(1)y=log3 (x- 2)
(3)
以下函数是对数函数吗?
NO!
判断一个函数是不是对数函数,我们必须严格按照定义的形式去判断!
(1)由x- 2>0 ,得 ,∴函数
的定义域是;
解:
(1) y=log3 (x- 2)
(2) y=log2(x2 +1)
(2)因为真数恒大于零,所以函数的定义域为R。
返回
(1)由于函数 必过(1,0)点
因此,当 x- 2=1 即x=3时, y 必然等于0, 所以此函数必过(3,0)点。
(1) y=loga (x- 2)
(2) y=loga(x2 +1)
(2)由于函数必过 (1,0)点
因此,当x2 +1=1,即x=0时,y 必然等于0,所以此函数必过(0,0)点。
返回
考察对数函数 y=log3x ,因为它的底数3>1,所以它在(0, + )上是增函数,于是
(1) log30.8,
log33.7
log30.8 < log33.7
返回
log0.54.2 < log0.52.9
log0.52.9
(2) log0.54.2,
考察对数函数 y=log0.5x ,因为它的底数0.5<1,所以它在(0, + )上是减函数,于是
返回
(3) loga5.9,
loga3.1
(0分析:
对数中函数的增减性决定于对数的底数是大于还是小于1,而由已知条件中并未明确指出底数中a于1的大小,因此需要对底数a进行讨论:
当a>1时,函数y=logax在(0,+ )上是 增函数,于是 loga5.9 > loga3.1
当0返回
a>1
0
象
性
质
1.定义域:R
2.值域:(0,+∞)
3.过定点(0,1),即x=0时,y=1
4. 当x>0时, y>1;
当x<0时,0
5.在 R上是增函数
在R上是减函数
回顾指数函数图象及性质
现在有一张纸,我把这张纸对折一次就变成了两层;我对折两次纸就变成了四层;如果我们设把纸对折的次数为x,对折后纸的层数为y,那么,试建立y关于x的函数关系式。
你能写出这个X关于Y的函数的关系表达式吗
解:
2次
3次
提问:如果我发现对折后的纸有4层,那么我对折了多少次?
如果我发现对折后的纸有8层,那么我对折了多少次?
… … 16层呢,32层呢 … …
我们可以发现:x关于y也可以建立一个函数。
指数式化对数式
这个就是我们要的函数关系
交换X和Y,以符合习惯
一般地,函数
就叫做对数函数。x为它的自变
对数函数的定义
以上两个函数也是对数函数!
量,函数的定义域为
提问:
我们知道,函数
和
互为反函数。
函数
和
是什么关系呢?
函数
和
互为反函数!
2.利用对称性画图.
因为指数函数y=ax (0
X
Y=ax (a>1)
Y
O
1
1
2
2
3
3
4
4
5
5
6
7
Y=logax (a>1)
Y=X
-1
-1
-2
●
●
●
●
●
●
●
●
●
●
X
Y
O
1
1
2
2
3
3
4
4
5
5
6
7
Y=X
-1
-1
-2
●
●
●
●
●
●
●
●
1
1
a>1
1
1
0
根据对数函数的图象描述对数函数的性质:
图像的特征 函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占满了整个y轴;
值域: R
3. 过(1.0)点
当x=1时,y=0。
增函数
4. 单调性:
a>1时,图像上升;
5. 函数值分布:
a>1:
当:x>1时, 图像在y轴上方;
当0
当0
图像的特征 函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占满了整个y轴;
值域: R
3. 过(1.0)点
当x=1时,y=0。
4. 单调性:
0
5. 函数值分布:
当 0
当:x>1, 则y<0
当:0
0
值域: R
当x=1时,y=0。
当:x>1时, 图像在y轴上方;
图像的特征 函数性质
2. 图像在y轴的投影占
满了整个y轴;
1.图像位于y轴右侧;
定义域:x>0
3. 过(1.0)点
4. 单调性:
增函数
0
a>1时,图像上升;
0
当:x>1, 则y<0
当0
a>1:
当0
当0
特殊点:
图
象
性
质
定义域:
值域:
单调性:
增函数
减函数
函 数值
的
分 布
当x>1, 则y>0;
当0
当0
对数函数图像及性质
名 称 指数函数 对数函数
一般形式
定义域
值域
单调性 a>1, 增函数
0
0
变
化情况 a>1: x>0, y>1
x<0, 0
0
0
图像关系 的图像于 的图像关于直线y=x对称
指数函数与对数函数对比
指数函数
对数函数
按要求回答问题
(1) y=log3 (x- 2)
(1)以上函数的定义域。
(2) y=log2(x2 +1)
(2)以上函数如果底数为
a(a>0且a ≠1)时,函数必过那一点。
例二:判断下列各组数中两个值的大小:
(1) log30.8,
log33.7
(3) loga5.9,
loga3.1
log0.52.9
(2) log0.54.2,
(0
2. 当a>1, 在 为增函数.
当0
作业:略
(2)y=log3 (-x)
(1)y=log3 (x- 2)
(3)
以下函数是对数函数吗?
NO!
判断一个函数是不是对数函数,我们必须严格按照定义的形式去判断!
(1)由x- 2>0 ,得 ,∴函数
的定义域是;
解:
(1) y=log3 (x- 2)
(2) y=log2(x2 +1)
(2)因为真数恒大于零,所以函数的定义域为R。
返回
(1)由于函数 必过(1,0)点
因此,当 x- 2=1 即x=3时, y 必然等于0, 所以此函数必过(3,0)点。
(1) y=loga (x- 2)
(2) y=loga(x2 +1)
(2)由于函数必过 (1,0)点
因此,当x2 +1=1,即x=0时,y 必然等于0,所以此函数必过(0,0)点。
返回
考察对数函数 y=log3x ,因为它的底数3>1,所以它在(0, + )上是增函数,于是
(1) log30.8,
log33.7
log30.8 < log33.7
返回
log0.54.2 < log0.52.9
log0.52.9
(2) log0.54.2,
考察对数函数 y=log0.5x ,因为它的底数0.5<1,所以它在(0, + )上是减函数,于是
返回
(3) loga5.9,
loga3.1
(0
对数中函数的增减性决定于对数的底数是大于还是小于1,而由已知条件中并未明确指出底数中a于1的大小,因此需要对底数a进行讨论:
当a>1时,函数y=logax在(0,+ )上是 增函数,于是 loga5.9 > loga3.1
当0
