2021-2022学年人教版数学八年级上册11.3.1 多边形 课件(第一课时 31张)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册11.3.1 多边形 课件(第一课时 31张) |  | |
| 格式 | zip | ||
| 文件大小 | 592.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 21:54:26 | ||
图片预览





文档简介
(共31张PPT)
人教版 数学 八年级上册
第3节 多边形及内角和
第1课时 多边形
第十一章 三角形
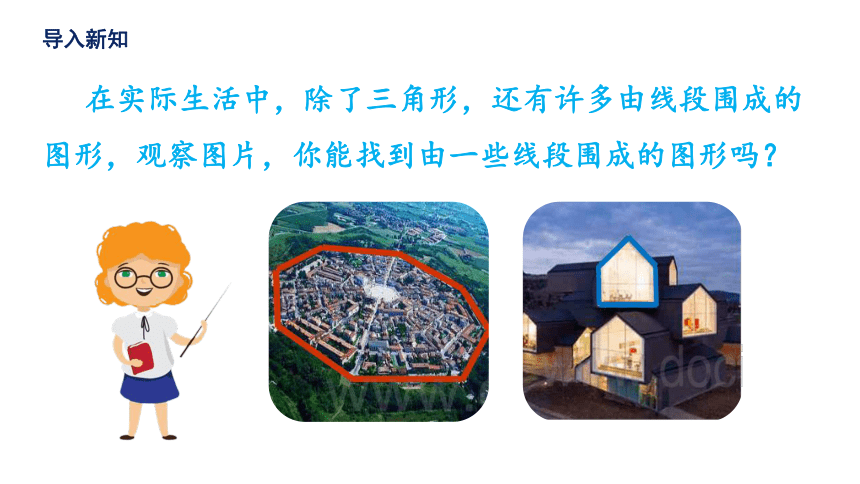
在实际生活中,除了三角形,还有许多由线段围成的图形,观察图片,你能找到由一些线段围成的图形吗?
导入新知
1.了解并掌握多边形的定义及有关概念,能区分凸凹多边形.
2.理解正多边形及其有关概念.
3.掌握对角线条数与多边形的边数之间的关系.
学习目标
问题1:什么是三角形?
问题2:类比三角形的概念,你能说出什么是多边形吗?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
新知一 多边形
合作探究
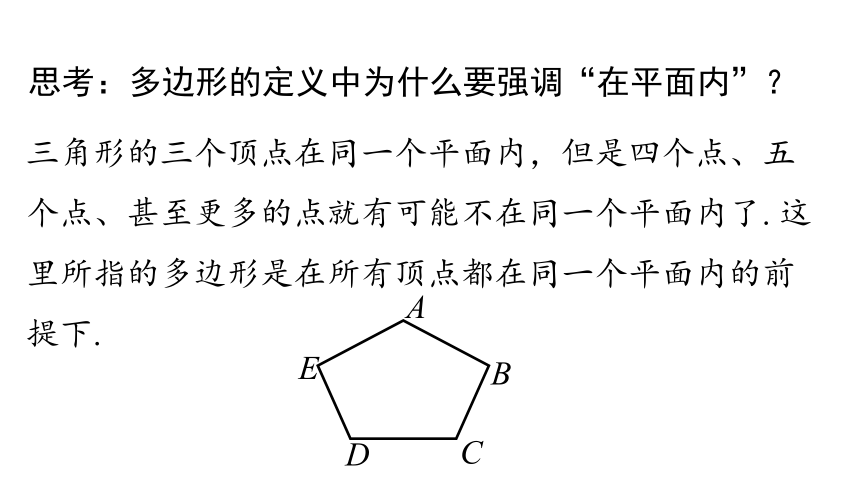
思考:多边形的定义中为什么要强调“在平面内”?
三角形的三个顶点在同一个平面内,但是四个点、五个点、甚至更多的点就有可能不在同一个平面内了. 这里所指的多边形是在所有顶点都在同一个平面内的前提下.
A
C
B
E
D
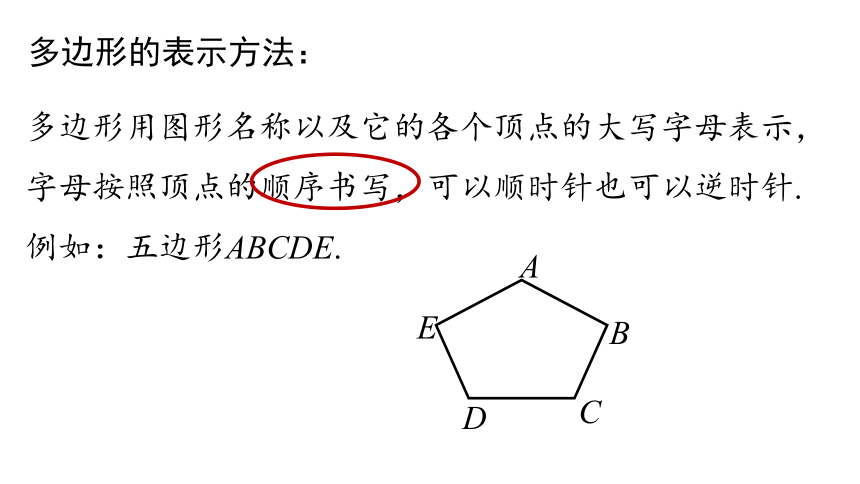
多边形用图形名称以及它的各个顶点的大写字母表示,字母按照顶点的顺序书写,可以顺时针也可以逆时针.
例如:五边形ABCDE.
多边形的表示方法:
A
C
B
E
D
类比三角形的概念,说明什么是多边形顶点、边、内角、外角?
A
C
B
E
D
F
如图:
顶点:A,B,C,D,E;
边:AB,BC,CD,DE,EA;
内角:∠A,∠B,∠C,∠D,∠AED
(多边形相邻两边组成的角叫做内角);
外角:∠DEF(多边形的边与它的
邻边的延长线组成的角).
新知二 多边形的相关概念
思考:三角形有3个顶点,3条边,3个内角、6个外角;四边形有4个顶点,4条边,4个内角、8个外角;
那么n边形有多少个顶点?多少条边?多少个内角?多少个外角?
归纳:1.多边形按照边数可以分为:三角形、四边形、五边形等,其中三角形是最简单的多边形.
2.n边形有n个顶点、n条边、n个内角、2n个外角.
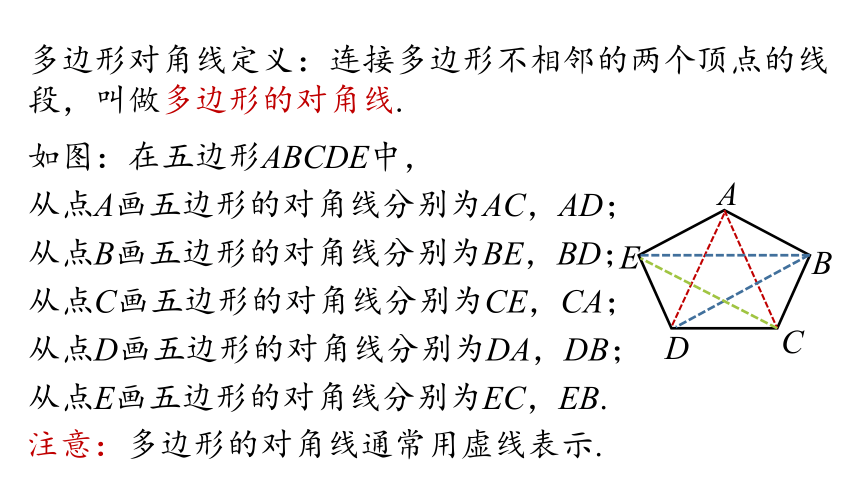
多边形对角线定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图:在五边形ABCDE中,
从点A画五边形的对角线分别为AC,AD;
从点B画五边形的对角线分别为BE,BD;
从点C画五边形的对角线分别为CE,CA;
从点D画五边形的对角线分别为DA,DB;
从点E画五边形的对角线分别为EC,EB.
A
C
B
E
D
注意:多边形的对角线通常用虚线表示.
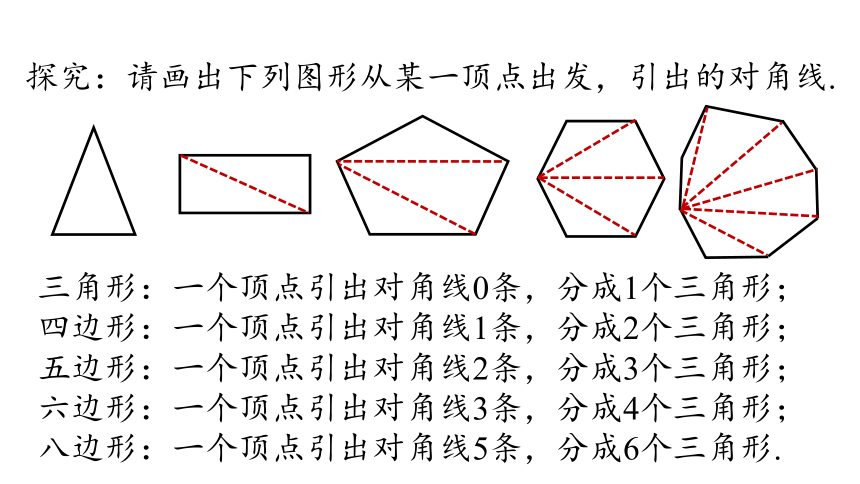
探究:请画出下列图形从某一顶点出发,引出的对角线.
三角形:一个顶点引出对角线0条,分成1个三角形;
四边形:一个顶点引出对角线1条,分成2个三角形;
五边形:一个顶点引出对角线2条,分成3个三角形;
六边形:一个顶点引出对角线3条,分成4个三角形;
八边形:一个顶点引出对角线5条,分成6个三角形.
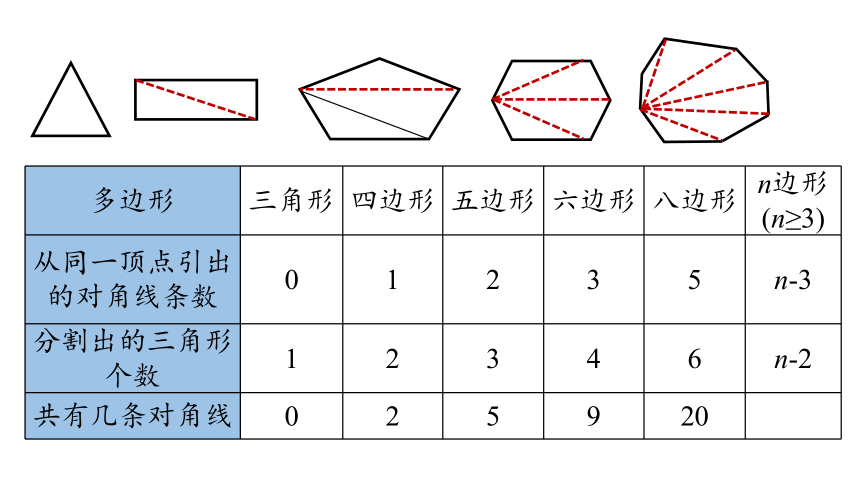
多边形 三角形 四边形 五边形 六边形 八边形 n边形(n≥3)
从同一顶点引出的对角线条数 0 1 2 3 5 n-3
分割出的三角形个数 1 2 3 4 6 n-2
共有几条对角线 0 2 5 9 20 .
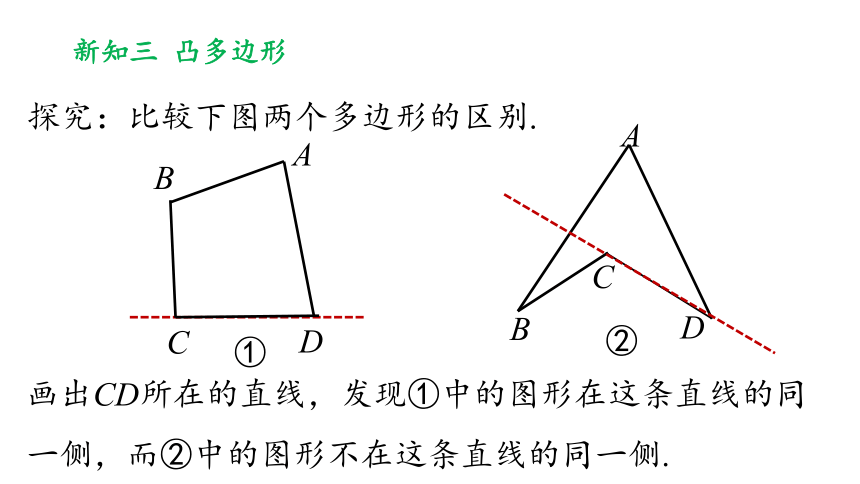
探究:比较下图两个多边形的区别.
A
D
C
B
A
C
B
D
①
②
画出CD所在的直线,发现①中的图形在这条直线的同一侧,而②中的图形不在这条直线的同一侧.
新知三 凸多边形
定义:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形. 反之,称为凹多边形,本节只讨论凸多边形.
凸多边形
A
D
C
B
A
C
B
D
①
②
等边三角形三边相等、三个内角相等;正方形四边相等四个内角相等;那么多边形是否具有这样的特殊情况?
正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形.
正三角形
(等边三角形)
正四边形
(正方形)
正五边形
正六边形
新知四 正多边形
下列图形是正多边形吗?如果不是,请说明为什么?
四边相等
四角相等
都不是.第一个不满足四个角相等,是菱形;第二个不满足四边相等,是长方形.
若一个多边形是正多边形,则必须同时满足各边、各角都相等.
2.下列多边形中不是凸多边形的是( )
1.画出下列图形的所有对角线.
B
巩固新知
多边形
定 义
对角线
正多边形
前提条件:同一个平面内
将多边形转化为三角形和四边形解决问题的重要线段
定义既是判定也是性质
归纳新知
1.下列图形中不是凸多边形的是( )
C
课后练习
2.对于多边形的外角,最准确的叙述是( )
A.外角是内角的对顶角
B.外角是内角的邻角
C.外角是与内角有公共顶点的角
D.外角是内角的邻补角
D
3.在凸多边形中,四边形有2条对角线,五边形有5条对角线,观察探索凸十边形的对角线有( )
A.29条 B.32条 C.35条 D.38条
C
4.从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为( )
A.4,3 B.3,3 C.3,4 D.4,4
C
5.下列说法不正确的是( )
A.正多边形的各边都相等
B.正多边形的各内角都相等
C.正四边形就是长方形
D.正三角形就是等边三角形
C
6.如图,把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长为( )
A.1 B.2 C.3 D.4
D
7.将一个正方形桌面砍下一个角后,桌子剩下的角的个数是( )
A.3个 B.4个
C.5个 D.3个或4个或5个
D
8.有一根长为32 cm的铁丝,请你按下列要求,弯成一个长方形或正方形,并分别计算它们的面积:
(1)长为10 cm,宽为6 cm的长方形;
解:10×6=60(cm2),面积为60 cm2;
(2)长为9 cm,宽为7 cm的长方形;
解:9×7=63(cm2),面积为63 cm2;
(3)边长为8 cm的正方形.
你发现在长与宽的变化过程中,其面积有什么规律?根据这一规律,请将总长为100 m的篱笆围成一个面积尽可能大的长方形或正方形.
解:8×8=64(cm2),面积为64 cm2.随着长与宽的差越来越小,其面积越来越大.
将总长为100 m的篱笆围成一个边长为25 m的正方形,其面积最大,最大面积为625 m2.
9.(1)如图①,O为四边形ABCD内一点,连接OA,OB,OC,OD,可以得到几个三角形?它与边数有何关系?
解:4个,与边数相等.
(2)如图②,点O在五边形ABCDE的AB边上,连接OC,OD,OE,可以得到几个三角形?它与边数有何关系?
解:4个,为边数减1.
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
解:4个,为边数减2.
再 见
人教版 数学 八年级上册
第3节 多边形及内角和
第1课时 多边形
第十一章 三角形
在实际生活中,除了三角形,还有许多由线段围成的图形,观察图片,你能找到由一些线段围成的图形吗?
导入新知
1.了解并掌握多边形的定义及有关概念,能区分凸凹多边形.
2.理解正多边形及其有关概念.
3.掌握对角线条数与多边形的边数之间的关系.
学习目标
问题1:什么是三角形?
问题2:类比三角形的概念,你能说出什么是多边形吗?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
新知一 多边形
合作探究
思考:多边形的定义中为什么要强调“在平面内”?
三角形的三个顶点在同一个平面内,但是四个点、五个点、甚至更多的点就有可能不在同一个平面内了. 这里所指的多边形是在所有顶点都在同一个平面内的前提下.
A
C
B
E
D
多边形用图形名称以及它的各个顶点的大写字母表示,字母按照顶点的顺序书写,可以顺时针也可以逆时针.
例如:五边形ABCDE.
多边形的表示方法:
A
C
B
E
D
类比三角形的概念,说明什么是多边形顶点、边、内角、外角?
A
C
B
E
D
F
如图:
顶点:A,B,C,D,E;
边:AB,BC,CD,DE,EA;
内角:∠A,∠B,∠C,∠D,∠AED
(多边形相邻两边组成的角叫做内角);
外角:∠DEF(多边形的边与它的
邻边的延长线组成的角).
新知二 多边形的相关概念
思考:三角形有3个顶点,3条边,3个内角、6个外角;四边形有4个顶点,4条边,4个内角、8个外角;
那么n边形有多少个顶点?多少条边?多少个内角?多少个外角?
归纳:1.多边形按照边数可以分为:三角形、四边形、五边形等,其中三角形是最简单的多边形.
2.n边形有n个顶点、n条边、n个内角、2n个外角.
多边形对角线定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图:在五边形ABCDE中,
从点A画五边形的对角线分别为AC,AD;
从点B画五边形的对角线分别为BE,BD;
从点C画五边形的对角线分别为CE,CA;
从点D画五边形的对角线分别为DA,DB;
从点E画五边形的对角线分别为EC,EB.
A
C
B
E
D
注意:多边形的对角线通常用虚线表示.
探究:请画出下列图形从某一顶点出发,引出的对角线.
三角形:一个顶点引出对角线0条,分成1个三角形;
四边形:一个顶点引出对角线1条,分成2个三角形;
五边形:一个顶点引出对角线2条,分成3个三角形;
六边形:一个顶点引出对角线3条,分成4个三角形;
八边形:一个顶点引出对角线5条,分成6个三角形.
多边形 三角形 四边形 五边形 六边形 八边形 n边形(n≥3)
从同一顶点引出的对角线条数 0 1 2 3 5 n-3
分割出的三角形个数 1 2 3 4 6 n-2
共有几条对角线 0 2 5 9 20 .
探究:比较下图两个多边形的区别.
A
D
C
B
A
C
B
D
①
②
画出CD所在的直线,发现①中的图形在这条直线的同一侧,而②中的图形不在这条直线的同一侧.
新知三 凸多边形
定义:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形. 反之,称为凹多边形,本节只讨论凸多边形.
凸多边形
A
D
C
B
A
C
B
D
①
②
等边三角形三边相等、三个内角相等;正方形四边相等四个内角相等;那么多边形是否具有这样的特殊情况?
正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形.
正三角形
(等边三角形)
正四边形
(正方形)
正五边形
正六边形
新知四 正多边形
下列图形是正多边形吗?如果不是,请说明为什么?
四边相等
四角相等
都不是.第一个不满足四个角相等,是菱形;第二个不满足四边相等,是长方形.
若一个多边形是正多边形,则必须同时满足各边、各角都相等.
2.下列多边形中不是凸多边形的是( )
1.画出下列图形的所有对角线.
B
巩固新知
多边形
定 义
对角线
正多边形
前提条件:同一个平面内
将多边形转化为三角形和四边形解决问题的重要线段
定义既是判定也是性质
归纳新知
1.下列图形中不是凸多边形的是( )
C
课后练习
2.对于多边形的外角,最准确的叙述是( )
A.外角是内角的对顶角
B.外角是内角的邻角
C.外角是与内角有公共顶点的角
D.外角是内角的邻补角
D
3.在凸多边形中,四边形有2条对角线,五边形有5条对角线,观察探索凸十边形的对角线有( )
A.29条 B.32条 C.35条 D.38条
C
4.从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为( )
A.4,3 B.3,3 C.3,4 D.4,4
C
5.下列说法不正确的是( )
A.正多边形的各边都相等
B.正多边形的各内角都相等
C.正四边形就是长方形
D.正三角形就是等边三角形
C
6.如图,把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长为( )
A.1 B.2 C.3 D.4
D
7.将一个正方形桌面砍下一个角后,桌子剩下的角的个数是( )
A.3个 B.4个
C.5个 D.3个或4个或5个
D
8.有一根长为32 cm的铁丝,请你按下列要求,弯成一个长方形或正方形,并分别计算它们的面积:
(1)长为10 cm,宽为6 cm的长方形;
解:10×6=60(cm2),面积为60 cm2;
(2)长为9 cm,宽为7 cm的长方形;
解:9×7=63(cm2),面积为63 cm2;
(3)边长为8 cm的正方形.
你发现在长与宽的变化过程中,其面积有什么规律?根据这一规律,请将总长为100 m的篱笆围成一个面积尽可能大的长方形或正方形.
解:8×8=64(cm2),面积为64 cm2.随着长与宽的差越来越小,其面积越来越大.
将总长为100 m的篱笆围成一个边长为25 m的正方形,其面积最大,最大面积为625 m2.
9.(1)如图①,O为四边形ABCD内一点,连接OA,OB,OC,OD,可以得到几个三角形?它与边数有何关系?
解:4个,与边数相等.
(2)如图②,点O在五边形ABCDE的AB边上,连接OC,OD,OE,可以得到几个三角形?它与边数有何关系?
解:4个,为边数减1.
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
解:4个,为边数减2.
再 见
