2021-2022学年人教版数学八年级上册11.3.2 多边形的内角和 课件(第二课时 30张)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册11.3.2 多边形的内角和 课件(第二课时 30张) |

|
|
| 格式 | zip | ||
| 文件大小 | 206.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-02 21:38:55 | ||
图片预览









文档简介
(共30张PPT)
人教版 数学 八年级上册
第3节 多边形及内角和
第2课时 多边形的内角和
第十一章 三角形
1.什么是多边形?
2.什么是多边形的对角线?多边形的对角线具有什么性质?
3.什么是正多边形?
4.由三角形内角和定理可以得到哪些推论?
5.三角形外角具有什么性质?
复习旧知
1.了解并掌握多边形内角和与外角和公式.
2.理解多边形内角和与外角和公式的推导过程.
3.灵活运用多边形的内角和与外角和定理解决实际问题.
学习目标
问题1:你能说出三角形的内角和是多少度吗?
三角形的内角和是180°.
问题2:你知道长方形和正方形的内角和是多少度吗?
长方形和正方形的内角和都是360°.
问题3:你能猜测任意一个四边形的内角和是多少度吗?
任意一个四边形的内角和是360°.
导入新知
探究:请大家任意画一个四边形,用量角器量出四个内角的大小,并计算出四个内角的和是多少?
经过测量发现四边形的四个内角和为360°.
试用三角形内角和定理来证明任意一个四边形的内角和为360°.利用对角线将四边形分成三角形来求解.
新知一 多边形的内角和
合作探究
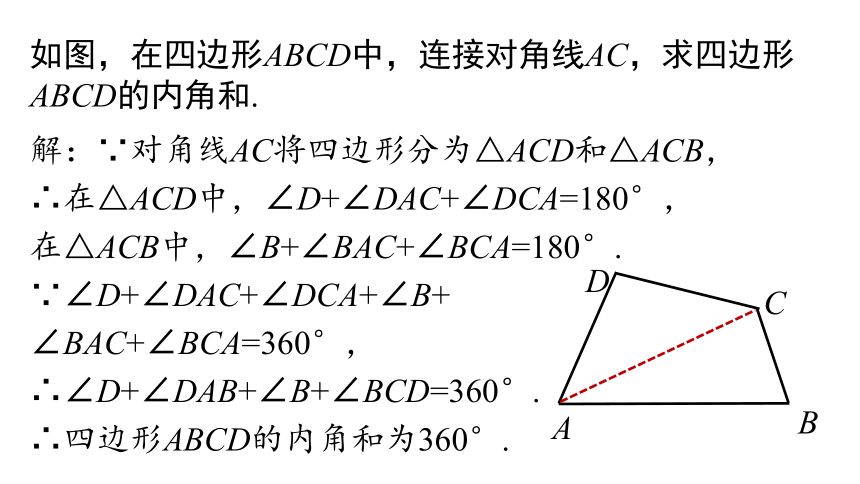
解:∵对角线AC将四边形分为△ACD和△ACB,
∴在△ACD中,∠D+∠DAC+∠DCA=180°,
在△ACB中,∠B+∠BAC+∠BCA=180°.
∵∠D+∠DAC+∠DCA+∠B+
∠BAC+∠BCA=360°,
∴∠D+∠DAB+∠B+∠BCD=360°.
∴四边形ABCD的内角和为360°.
如图,在四边形ABCD中,连接对角线AC,求四边形ABCD的内角和.
A
C
B
D
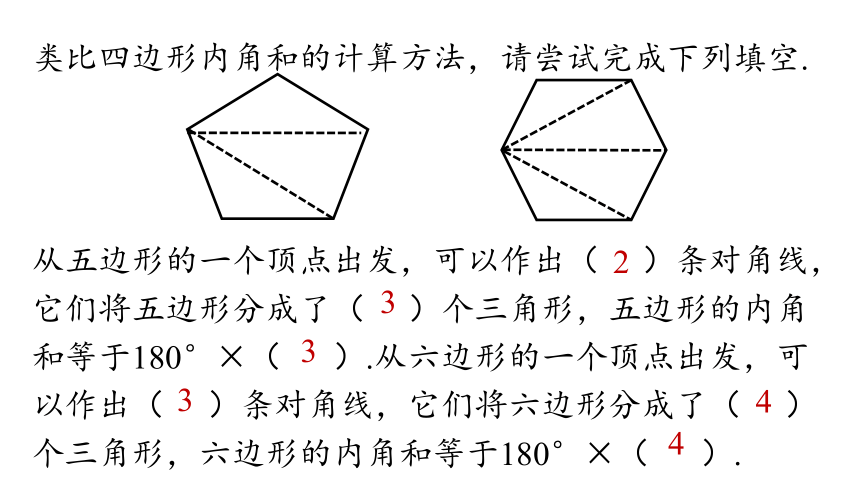
类比四边形内角和的计算方法,请尝试完成下列填空.
从五边形的一个顶点出发,可以作出( )条对角线,它们将五边形分成了( )个三角形,五边形的内角和等于180°×( ).从六边形的一个顶点出发,可以作出( )条对角线,它们将六边形分成了( )个三角形,六边形的内角和等于180°×( ).
2
3
3
3
4
4
多边形的内角和公式:
n边形的内角和等于(n-2)×180°.
通过以上的探究,我们发现多边形的内角和与边数之间有密切的关系.从n边形的一个顶点出发,可以作出(n-3)条对角线,它们将n边形分成了(n-2)个三角形,
n边形的内角和等于(n-2)× 180°.
例1 如果一个四边形的一组对角互补,那么另外一组对角有什么关系?
B
A
C
D
解:若在四边形ABCD中,∠A和∠C
互补,则∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=360°,
∴∠B+∠D=360 °-(∠A+∠C)=180°.
则∠B与∠D互为补角.
如果一个四边形的一组对角互补,那么另外一组对角也互补.
典例精析
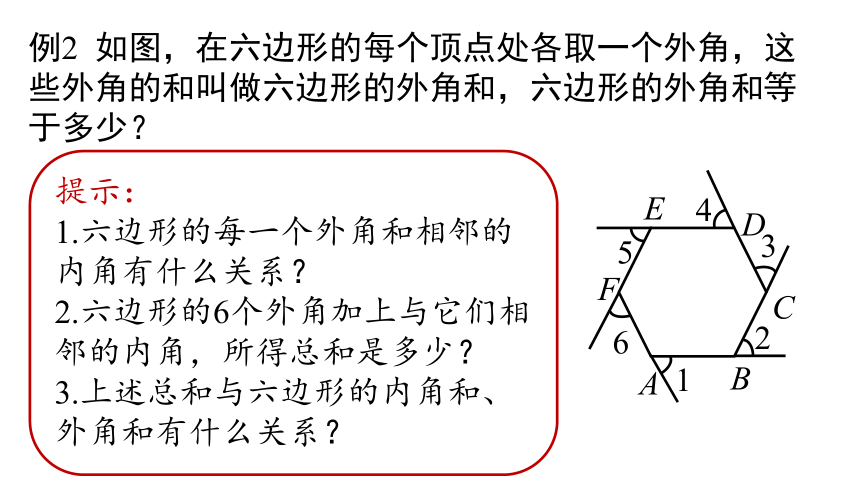
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少?
提示:
1.六边形的每一个外角和相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角,所得总和是多少?
3.上述总和与六边形的内角和、外角和有什么关系?
A
B
C
D
E
F
1
2
3
5
4
6
1.六边形的每一个外角和相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角,所得总
和是多少?
任意一个外角加上与它相邻的内角等于180°.
每一个外角加上与它相邻的内角等于180°,所以六个外角加上与它们相邻的内角等于180°×6.
3.上述总和与六边形的内角和、外角和有什么关系?
如果是n边形,会得出什么结论呢?
六个外角加上与它们相邻的内角等于180°×6=1080°,
六边形的内角和为180°×4=720°,
六边形的外角和为180°×6-180°×4=360°.
在n边形的每个顶点处各取一个外角,n边形的外角和等于多少?
性质:多边形的外角和等于360°.
n个外角加上与它们相邻的内角等于180°×n,n边形的内角和为180°×
(n-2),n边形的外角和为180°×n-180°×(n-2)=360°.
新知二 多边形的外角和
A
B
C
D
E
F
1
2
3
5
4
6
合作探究
从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向,在行程中所转的各个角的和,就是多边形的外角和. 由于走了一周,所转的各个角的和就等于一个周角,所以多边形的外角和等于360°.
A
B
C
D
E
F
1
2
3
5
4
6
性质:多边形的外角和等于360°.
例3 求出下列图形中x的值.
解:(1)四边形的内角和为360°,
则x°+x°+140°+90°=360°,解得x=65.
(2)四边形的内角和为360°,
则∠1+75°+120°+80°=360°,解得∠1=85°,
因为∠1+x°=180°,所以x=95.
120°
80°
75°
x°
┐
140°
x°
x°
1
(1)
(2)
典例精析
例4 一个多边形的各内角都等于120°,它是几边形?
解:设这个多边形的边数为n,
因为各内角都等于120°,所以内角和为120°×n.
由内角和公式得:(n-2)× 180°.
则120° ×n=(n-2)× 180° ,解得n=6.
所以它是六边形.
你能从多边形外角和的
角度想出另外的解法吗?
方法二 解:设这个多边形的边数为n,
因为各内角都等于120 ° ,所以各外角都等于180 °-120 °=60 °.
由外角和性质得:n×60°=360°,
解得n=6.
所以它是六边形.
例4 一个多边形的各内角都等于120°,它是几边形?
多边形的
内角和
内角和计算公式
外角和
正多边形
(n-2)×180°(n为≥3的整数)
多边形的外角和等于360°(与边数无关)
内角= ,
外角=
归纳新知
1.【2020·淮安】六边形的内角和为( )
A.360° B.540°
C.720° D.1 080°
C
课后练习
2.【2020·济宁】若一个多边形的内角和是1 080°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
B
3.【2020·岳阳】如图,DA⊥AB,CD⊥DA,若∠B=56°,则∠C的度数是( )
A.154°
B.144°
C.134°
D.124°
D
4.【中考·广安】若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.7 B.10 C.35 D.70
C
5.把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,则原多边形纸片的边数不可能是( )
A.16 B.17 C.18 D.19
A
6.【2019·铜仁】如图为长方形ABCD,一条直线将该长方形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360°
B.540°
C.630°
D.720°
C
7.一个多边形切去一个角后,形成的另一个多边形的内角和为1 080°,那么原多边形的边数为( )
A.7 B.7或8
C.8或9 D.7或8或9
D
8.(1)一个n边形,除了一个内角外,其余(n-1)个内角的和为2 770°,求这个内角的度数.
解:设这个内角的度数为x,
则(n-2)×180°-x=2 770°,
即180°·n=3 130°+x.
∵n为正整数,0°<x<180°,∴n=18.
∴这个内角的度数为180°×(18-2)-2 770°=110°.
(2)小李同学在计算一个n边形的内角和时不小心多加了一个内角,得到的内角之和是1 380°,则这个多边形的边数n的值是多少?多加的这个内角度数是多少?
解:设多加的这个内角度数为α,则(n-2)·180°=
1 380°-α.∵1 380°=7×180°+120°,多边形的内角和应是180°的倍数,∴n=9,α=120°.
答:这个多边形的边数n的值是9,多加的这个内角度数是120°.
9.在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
解:∵BE∥AD,∠D=80°,∠A=140°,
∴∠BEC=∠D=80°,∠ABE=180°-
∠A=180°-140°=40°.又∵BE平分∠ABC,
∴∠EBC=∠ABE=40°.∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.
再 见
人教版 数学 八年级上册
第3节 多边形及内角和
第2课时 多边形的内角和
第十一章 三角形
1.什么是多边形?
2.什么是多边形的对角线?多边形的对角线具有什么性质?
3.什么是正多边形?
4.由三角形内角和定理可以得到哪些推论?
5.三角形外角具有什么性质?
复习旧知
1.了解并掌握多边形内角和与外角和公式.
2.理解多边形内角和与外角和公式的推导过程.
3.灵活运用多边形的内角和与外角和定理解决实际问题.
学习目标
问题1:你能说出三角形的内角和是多少度吗?
三角形的内角和是180°.
问题2:你知道长方形和正方形的内角和是多少度吗?
长方形和正方形的内角和都是360°.
问题3:你能猜测任意一个四边形的内角和是多少度吗?
任意一个四边形的内角和是360°.
导入新知
探究:请大家任意画一个四边形,用量角器量出四个内角的大小,并计算出四个内角的和是多少?
经过测量发现四边形的四个内角和为360°.
试用三角形内角和定理来证明任意一个四边形的内角和为360°.利用对角线将四边形分成三角形来求解.
新知一 多边形的内角和
合作探究
解:∵对角线AC将四边形分为△ACD和△ACB,
∴在△ACD中,∠D+∠DAC+∠DCA=180°,
在△ACB中,∠B+∠BAC+∠BCA=180°.
∵∠D+∠DAC+∠DCA+∠B+
∠BAC+∠BCA=360°,
∴∠D+∠DAB+∠B+∠BCD=360°.
∴四边形ABCD的内角和为360°.
如图,在四边形ABCD中,连接对角线AC,求四边形ABCD的内角和.
A
C
B
D
类比四边形内角和的计算方法,请尝试完成下列填空.
从五边形的一个顶点出发,可以作出( )条对角线,它们将五边形分成了( )个三角形,五边形的内角和等于180°×( ).从六边形的一个顶点出发,可以作出( )条对角线,它们将六边形分成了( )个三角形,六边形的内角和等于180°×( ).
2
3
3
3
4
4
多边形的内角和公式:
n边形的内角和等于(n-2)×180°.
通过以上的探究,我们发现多边形的内角和与边数之间有密切的关系.从n边形的一个顶点出发,可以作出(n-3)条对角线,它们将n边形分成了(n-2)个三角形,
n边形的内角和等于(n-2)× 180°.
例1 如果一个四边形的一组对角互补,那么另外一组对角有什么关系?
B
A
C
D
解:若在四边形ABCD中,∠A和∠C
互补,则∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=360°,
∴∠B+∠D=360 °-(∠A+∠C)=180°.
则∠B与∠D互为补角.
如果一个四边形的一组对角互补,那么另外一组对角也互补.
典例精析
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少?
提示:
1.六边形的每一个外角和相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角,所得总和是多少?
3.上述总和与六边形的内角和、外角和有什么关系?
A
B
C
D
E
F
1
2
3
5
4
6
1.六边形的每一个外角和相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角,所得总
和是多少?
任意一个外角加上与它相邻的内角等于180°.
每一个外角加上与它相邻的内角等于180°,所以六个外角加上与它们相邻的内角等于180°×6.
3.上述总和与六边形的内角和、外角和有什么关系?
如果是n边形,会得出什么结论呢?
六个外角加上与它们相邻的内角等于180°×6=1080°,
六边形的内角和为180°×4=720°,
六边形的外角和为180°×6-180°×4=360°.
在n边形的每个顶点处各取一个外角,n边形的外角和等于多少?
性质:多边形的外角和等于360°.
n个外角加上与它们相邻的内角等于180°×n,n边形的内角和为180°×
(n-2),n边形的外角和为180°×n-180°×(n-2)=360°.
新知二 多边形的外角和
A
B
C
D
E
F
1
2
3
5
4
6
合作探究
从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向,在行程中所转的各个角的和,就是多边形的外角和. 由于走了一周,所转的各个角的和就等于一个周角,所以多边形的外角和等于360°.
A
B
C
D
E
F
1
2
3
5
4
6
性质:多边形的外角和等于360°.
例3 求出下列图形中x的值.
解:(1)四边形的内角和为360°,
则x°+x°+140°+90°=360°,解得x=65.
(2)四边形的内角和为360°,
则∠1+75°+120°+80°=360°,解得∠1=85°,
因为∠1+x°=180°,所以x=95.
120°
80°
75°
x°
┐
140°
x°
x°
1
(1)
(2)
典例精析
例4 一个多边形的各内角都等于120°,它是几边形?
解:设这个多边形的边数为n,
因为各内角都等于120°,所以内角和为120°×n.
由内角和公式得:(n-2)× 180°.
则120° ×n=(n-2)× 180° ,解得n=6.
所以它是六边形.
你能从多边形外角和的
角度想出另外的解法吗?
方法二 解:设这个多边形的边数为n,
因为各内角都等于120 ° ,所以各外角都等于180 °-120 °=60 °.
由外角和性质得:n×60°=360°,
解得n=6.
所以它是六边形.
例4 一个多边形的各内角都等于120°,它是几边形?
多边形的
内角和
内角和计算公式
外角和
正多边形
(n-2)×180°(n为≥3的整数)
多边形的外角和等于360°(与边数无关)
内角= ,
外角=
归纳新知
1.【2020·淮安】六边形的内角和为( )
A.360° B.540°
C.720° D.1 080°
C
课后练习
2.【2020·济宁】若一个多边形的内角和是1 080°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
B
3.【2020·岳阳】如图,DA⊥AB,CD⊥DA,若∠B=56°,则∠C的度数是( )
A.154°
B.144°
C.134°
D.124°
D
4.【中考·广安】若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.7 B.10 C.35 D.70
C
5.把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,则原多边形纸片的边数不可能是( )
A.16 B.17 C.18 D.19
A
6.【2019·铜仁】如图为长方形ABCD,一条直线将该长方形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360°
B.540°
C.630°
D.720°
C
7.一个多边形切去一个角后,形成的另一个多边形的内角和为1 080°,那么原多边形的边数为( )
A.7 B.7或8
C.8或9 D.7或8或9
D
8.(1)一个n边形,除了一个内角外,其余(n-1)个内角的和为2 770°,求这个内角的度数.
解:设这个内角的度数为x,
则(n-2)×180°-x=2 770°,
即180°·n=3 130°+x.
∵n为正整数,0°<x<180°,∴n=18.
∴这个内角的度数为180°×(18-2)-2 770°=110°.
(2)小李同学在计算一个n边形的内角和时不小心多加了一个内角,得到的内角之和是1 380°,则这个多边形的边数n的值是多少?多加的这个内角度数是多少?
解:设多加的这个内角度数为α,则(n-2)·180°=
1 380°-α.∵1 380°=7×180°+120°,多边形的内角和应是180°的倍数,∴n=9,α=120°.
答:这个多边形的边数n的值是9,多加的这个内角度数是120°.
9.在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
解:∵BE∥AD,∠D=80°,∠A=140°,
∴∠BEC=∠D=80°,∠ABE=180°-
∠A=180°-140°=40°.又∵BE平分∠ABC,
∴∠EBC=∠ABE=40°.∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.
再 见
