广东省广州市番禹中学数学选修一 22《双曲线的标准方程》课件
文档属性
| 名称 | 广东省广州市番禹中学数学选修一 22《双曲线的标准方程》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 46.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-09 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
1.椭圆是如何定义的?椭圆的标准方程是怎样的?
【复习引入】
2.已知椭圆的标准方程,如何确定a、b的值及
焦点坐标?
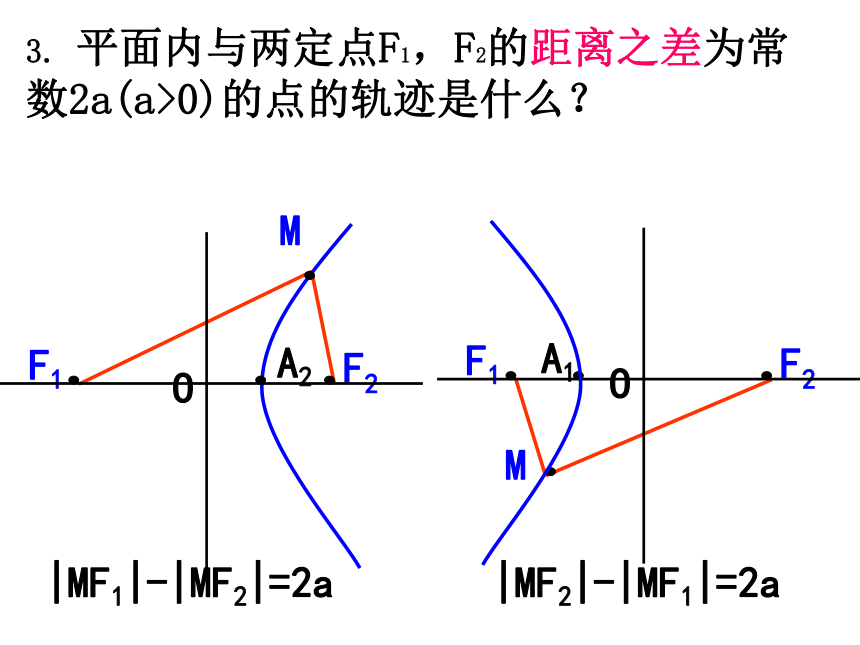
平面内与两个定点F1,F2 的距离之和等于常数
2a(大于|F1F2| )的点的轨迹叫做椭圆.
以大小定焦点
A2
O
F1
F2
M
O
F1
F2
M
A1
|MF1|-|MF2|=2a
|MF2|-|MF1|=2a
3. 平面内与两定点F1,F2的距离之差为常数2a(a>0)的点的轨迹是什么?
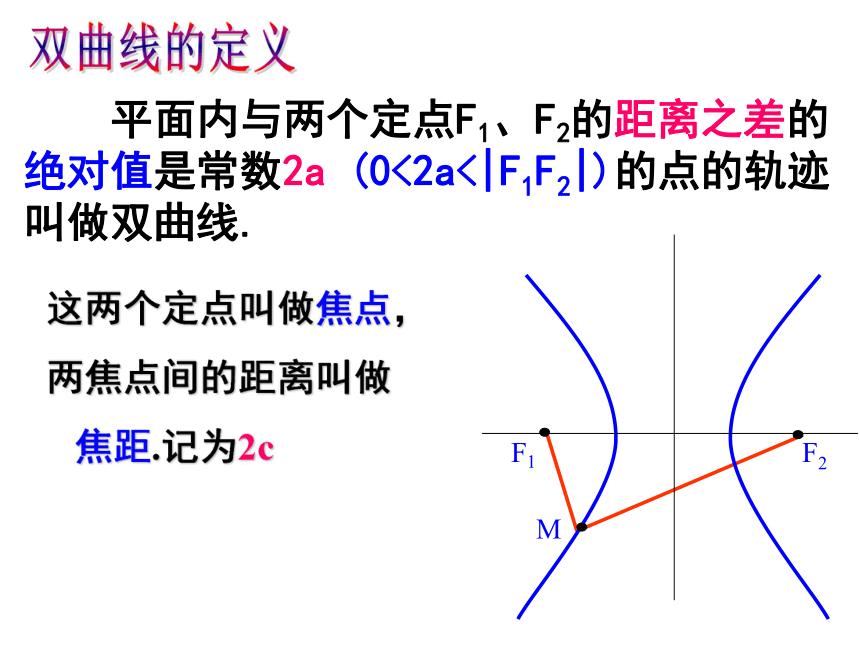
平面内与两个定点F1、F2的距离之差的绝对值是常数2a (0<2a<|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做焦点,
两焦点间的距离叫做
焦距.记为2c
F1
F2
M
【问题思考】
1.若去掉定义中的绝对值,动点的轨迹是什么?
2.若定义中的常数2a=0,动点的轨迹是什么?
3.若定义中的常数2a=|F1F2|,动点的轨迹是什么?
轨迹为双曲线的一支.
轨迹为F1F2的垂直平分线.
轨迹为以F1、F2端点的两条射线.
O
F1
F2
M
y
x
F1
F2
M
y
x
例1. 已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
例2.根据下列方程,求出a、b、c的值及焦点坐标.
椭圆方程中: 以大小定a、b定焦点;
双曲线方程中:以正负定a、b定焦点.
定义
图象
方程
焦点
a.b.c 的关系
| |MF1|-|MF2| | =2a(2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
作业:课本P53 1、2、3,P58 A组1
定义
图象
方程
焦点
a、b、c
的关系
如何确定焦点位置
| |MF1|-|MF2| | =2a(0<2a<|F1F2|)
( ±c, 0) (0, ± c)
以正负定a、b定焦点.
【例与练】
2.求下列双曲线的焦距与焦点坐标:
3.已知方程
(1)若方程表示焦点在x轴的椭圆,求m的范围;
(2)若方程表示焦点在y轴的双曲线,求m的范围;
(3)若方程表示双曲线,求m的取值范围.
(1)求证C1与C2有相同的焦点F1、F2;
(2)若P是C1、C2的一个交点,求
ΔPF1F2的面积.
5.求满足下列条件的双曲线的标准方程:
(1)与 焦点,且经过点(2,-5)
(2)过点
6.已知A、B两地相距800米,在A地听到炮弹爆炸声比在B地晚2秒,若声速为340m/s,求炮弹爆炸点的轨迹方程.
作业:课本P58 A组 2、B组2
《同步导学》P39 (1)~(7)
补充(4班选做)
求与圆A:(x+2)2+y2=1外切,且过点B(2,0)的动圆圆心P的轨迹.
3.已知 a=8,c=10,F1、F2为双曲线的焦点(1)若|PF1|= 9 ,求|PF2|;
(2)若△MNF2的边MN过F1,且M、N在同一支
上,若|MN|=7,求△MF2N的周长.
1.椭圆是如何定义的?椭圆的标准方程是怎样的?
【复习引入】
2.已知椭圆的标准方程,如何确定a、b的值及
焦点坐标?
平面内与两个定点F1,F2 的距离之和等于常数
2a(大于|F1F2| )的点的轨迹叫做椭圆.
以大小定焦点
A2
O
F1
F2
M
O
F1
F2
M
A1
|MF1|-|MF2|=2a
|MF2|-|MF1|=2a
3. 平面内与两定点F1,F2的距离之差为常数2a(a>0)的点的轨迹是什么?
平面内与两个定点F1、F2的距离之差的绝对值是常数2a (0<2a<|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做焦点,
两焦点间的距离叫做
焦距.记为2c
F1
F2
M
【问题思考】
1.若去掉定义中的绝对值,动点的轨迹是什么?
2.若定义中的常数2a=0,动点的轨迹是什么?
3.若定义中的常数2a=|F1F2|,动点的轨迹是什么?
轨迹为双曲线的一支.
轨迹为F1F2的垂直平分线.
轨迹为以F1、F2端点的两条射线.
O
F1
F2
M
y
x
F1
F2
M
y
x
例1. 已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
例2.根据下列方程,求出a、b、c的值及焦点坐标.
椭圆方程中: 以大小定a、b定焦点;
双曲线方程中:以正负定a、b定焦点.
定义
图象
方程
焦点
a.b.c 的关系
| |MF1|-|MF2| | =2a(2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
作业:课本P53 1、2、3,P58 A组1
定义
图象
方程
焦点
a、b、c
的关系
如何确定焦点位置
| |MF1|-|MF2| | =2a(0<2a<|F1F2|)
( ±c, 0) (0, ± c)
以正负定a、b定焦点.
【例与练】
2.求下列双曲线的焦距与焦点坐标:
3.已知方程
(1)若方程表示焦点在x轴的椭圆,求m的范围;
(2)若方程表示焦点在y轴的双曲线,求m的范围;
(3)若方程表示双曲线,求m的取值范围.
(1)求证C1与C2有相同的焦点F1、F2;
(2)若P是C1、C2的一个交点,求
ΔPF1F2的面积.
5.求满足下列条件的双曲线的标准方程:
(1)与 焦点,且经过点(2,-5)
(2)过点
6.已知A、B两地相距800米,在A地听到炮弹爆炸声比在B地晚2秒,若声速为340m/s,求炮弹爆炸点的轨迹方程.
作业:课本P58 A组 2、B组2
《同步导学》P39 (1)~(7)
补充(4班选做)
求与圆A:(x+2)2+y2=1外切,且过点B(2,0)的动圆圆心P的轨迹.
3.已知 a=8,c=10,F1、F2为双曲线的焦点(1)若|PF1|= 9 ,求|PF2|;
(2)若△MNF2的边MN过F1,且M、N在同一支
上,若|MN|=7,求△MF2N的周长.
