八年级数学三角形中的边角关系
图片预览





文档简介
(共18张PPT)
14.1
思 考
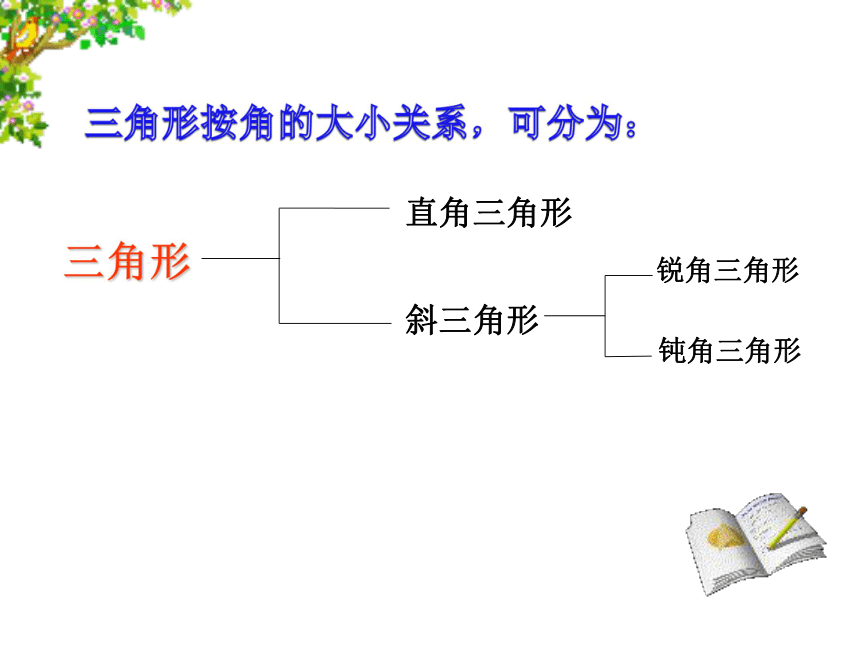
三角形若按角来分类,分为哪几类?
等腰三角形(等边三角形是它的特例)
不等边三角形
三角形
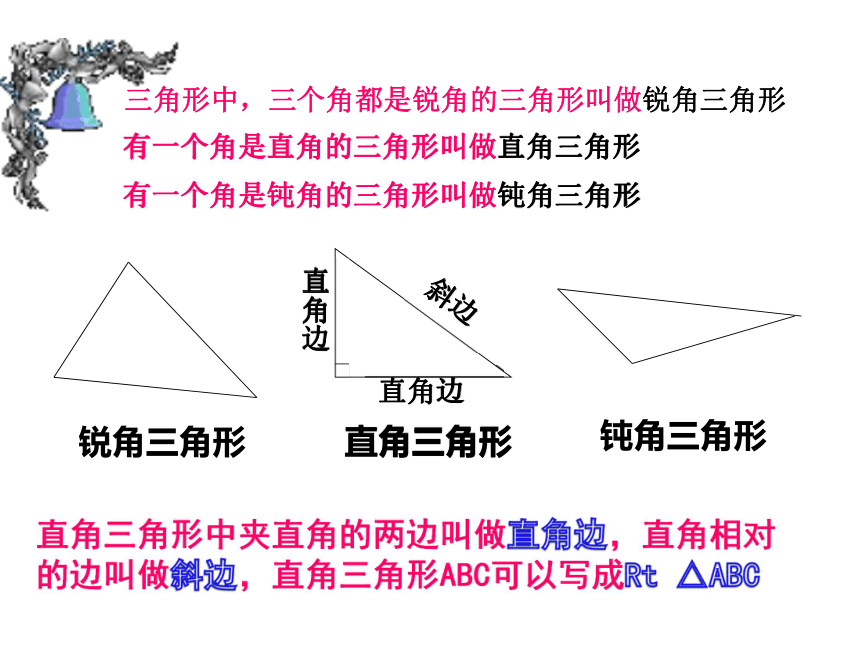
三角形中,三个角都是锐角的三角形叫做锐角三角形
锐角三角形
有一个角是直角的三角形叫做直角三角形
有一个角是钝角的三角形叫做钝角三角形
直角边
直角边
斜边
直角三角形
钝角三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
1
2
3
1
2
3
1
2
3
1
3
2
1
2
3
1
2
3
3
2
1
解: 由于BD⊥AC,(已知)
所以∠ADB=∠CDB=90°.
在△ABD中,
∠A+ ∠ABD+ ∠ADB=180°,(三角形的
三个内角和等于180°)
∠ABD=54°,∠ADB=90°.(已知)
∠A=180°- 54°- 90°= 36°
在△ABC中,
∠C=180°- 36°- (54°+ 18°) =72°
例1 已知:如图,△ABC中,BD⊥AC,垂足为D。∠ABD=54°,∠DBC=18°.
求∠A和∠C的度数。
B
C
A
D
┒
例2 在△ABC 中,若∠A:∠B:∠C =2:3:4,求∠A 、∠B 和∠C 的度数.
解:设∠A=2x,则∠B=3x, ∠C=4x.
∴2x+3x+4x=180° (三角形的三个内角和等于180°)
解方程,得x=20°
∴ ∠A=2×20 ° = 40 °
∠B=3×20 ° = 60 °
∠C=4×20 ° = 80 °
一 、选择题
(1) 在△ABC中,∠A =50 °, ∠B =110 °,则∠C =( )
A. 30 ° B. 20 ° C. 10 ° D. 50 °
(2)在△ABC中,∠A =80 °, ∠B =∠C,则∠B =( )
A. 50 ° B. 40 ° C. 30 ° D. 45 °
二、填空
(1)在△ABC中,∠A =105 °,∠B- ∠C =15 °,则∠C =
(2)在△ABC中, ∠A:∠B :∠C = 3: 4 : 5, 则∠C =
75°
B
30°
A
试一试
△ ABC满足下列条件时, 它是锐角三角形、
直角三角形还是钝角三角形?
(1)∠A =∠B =∠C;
(2) ∠A+∠B =∠C;
(3)∠A=∠B = 30°.
说一说
如图,已知:在△ABC中,AD ⊥ BC,垂足是D, ∠B=70°,∠BAC=46°.求∠CAD的度数.
练一练
B
C
A
D
┒
(一)三角形按角分类;
(二)三角形的三个内角和等于180°;
(三)利用代数中列方程的方法可以求角的度数.
回顾与小结
本节课里你有哪些收获?
71页,练习题1、3题。
作业:
74页,习题14.1
第 3、5 题。
课后再探索:
1、一个三角形最多有几个直角?为什么?
2、一个三角形最多有几个钝角?为什么?
3、一个三角形最多有几个锐角?最少有几个锐角?
4、你能否利用三角形的内角和,求出四边形、五边形的内角和?
14.1
思 考
三角形若按角来分类,分为哪几类?
等腰三角形(等边三角形是它的特例)
不等边三角形
三角形
三角形中,三个角都是锐角的三角形叫做锐角三角形
锐角三角形
有一个角是直角的三角形叫做直角三角形
有一个角是钝角的三角形叫做钝角三角形
直角边
直角边
斜边
直角三角形
钝角三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
1
2
3
1
2
3
1
2
3
1
3
2
1
2
3
1
2
3
3
2
1
解: 由于BD⊥AC,(已知)
所以∠ADB=∠CDB=90°.
在△ABD中,
∠A+ ∠ABD+ ∠ADB=180°,(三角形的
三个内角和等于180°)
∠ABD=54°,∠ADB=90°.(已知)
∠A=180°- 54°- 90°= 36°
在△ABC中,
∠C=180°- 36°- (54°+ 18°) =72°
例1 已知:如图,△ABC中,BD⊥AC,垂足为D。∠ABD=54°,∠DBC=18°.
求∠A和∠C的度数。
B
C
A
D
┒
例2 在△ABC 中,若∠A:∠B:∠C =2:3:4,求∠A 、∠B 和∠C 的度数.
解:设∠A=2x,则∠B=3x, ∠C=4x.
∴2x+3x+4x=180° (三角形的三个内角和等于180°)
解方程,得x=20°
∴ ∠A=2×20 ° = 40 °
∠B=3×20 ° = 60 °
∠C=4×20 ° = 80 °
一 、选择题
(1) 在△ABC中,∠A =50 °, ∠B =110 °,则∠C =( )
A. 30 ° B. 20 ° C. 10 ° D. 50 °
(2)在△ABC中,∠A =80 °, ∠B =∠C,则∠B =( )
A. 50 ° B. 40 ° C. 30 ° D. 45 °
二、填空
(1)在△ABC中,∠A =105 °,∠B- ∠C =15 °,则∠C =
(2)在△ABC中, ∠A:∠B :∠C = 3: 4 : 5, 则∠C =
75°
B
30°
A
试一试
△ ABC满足下列条件时, 它是锐角三角形、
直角三角形还是钝角三角形?
(1)∠A =∠B =∠C;
(2) ∠A+∠B =∠C;
(3)∠A=∠B = 30°.
说一说
如图,已知:在△ABC中,AD ⊥ BC,垂足是D, ∠B=70°,∠BAC=46°.求∠CAD的度数.
练一练
B
C
A
D
┒
(一)三角形按角分类;
(二)三角形的三个内角和等于180°;
(三)利用代数中列方程的方法可以求角的度数.
回顾与小结
本节课里你有哪些收获?
71页,练习题1、3题。
作业:
74页,习题14.1
第 3、5 题。
课后再探索:
1、一个三角形最多有几个直角?为什么?
2、一个三角形最多有几个钝角?为什么?
3、一个三角形最多有几个锐角?最少有几个锐角?
4、你能否利用三角形的内角和,求出四边形、五边形的内角和?
