期中复习测评 第1章反比例函数 2021-2022学年湘教版九年级数学上册(word版含答案)
文档属性
| 名称 | 期中复习测评 第1章反比例函数 2021-2022学年湘教版九年级数学上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 359.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 14:10:30 | ||
图片预览


文档简介
2021-2022学年湘教版九年级数学上册《第1章反比例函数》期中复习测评(附答案)
一.选择题(共10小题,满分30分)
1.下列关系式中,y是x的反比例函数的是( )
A.y=4x B.=3 C.y=﹣ D.y=x2﹣1
2.一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
3.已知函数y=kx中y随x的增大而减小,那么它和函数y=在同一平面直角坐标系内的大致图象可能是( )
A.B.C.D.
4.如图,点P(﹣2a,a)是反比例函数y=与⊙O的一个交点,图中阴影部分的面积为10π,则该反比例函数的表达式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=﹣
5.反比例函数的图象在第一、第三象限,则m可能取的一个值为( )
A.0 B.1 C.2 D.3
6.如图,直线x=t(t>0)与反比例函数y=(x>0)、y=(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )
A.2 B.3 C.4 D.5
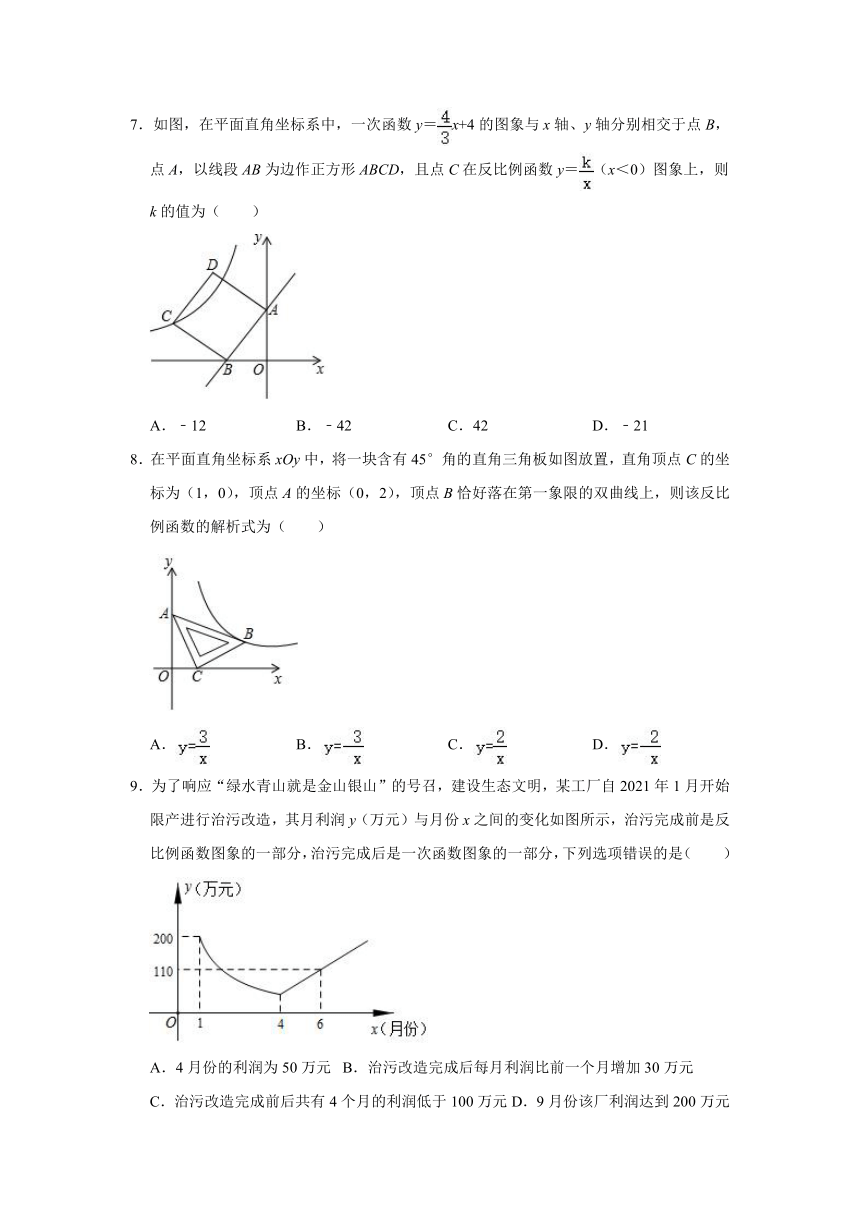
7.如图,在平面直角坐标系中,一次函数y=x+4的图象与x轴、y轴分别相交于点B,点A,以线段AB为边作正方形ABCD,且点C在反比例函数y=(x<0)图象上,则k的值为( )
A.﹣12 B.﹣42 C.42 D.﹣21
8.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标(0,2),顶点B恰好落在第一象限的双曲线上,则该反比例函数的解析式为( )
A. B. C. D.
9.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2021年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元 B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元D.9月份该厂利润达到200万元
10.如图,曲线表示温度T(℃)与时间t(h)之间的函数关系,它是一个反比例函数的图象的一支.当温度T≤2℃时,时间t应( )
A.不小于h B.不大于h C.不小于h D.不大于h
二.填空题(共8小题,满分24分)
11.已知:是反比例函数,则m= .
12.某厂计划建造一个容积为5×104m3的长方体蓄水池,则蓄水池的底面积S(m2)与其深度h(m)的函数关系式是 .
13.反比例函数y=(x<0)的图象如图所示,则m的取值范围为 .
14.直线y=k1x+b与双曲线y=在同一平面直角坐标系中的图象如图所示,则关于x的不等式>k1x+b的解集为 .
15.如图所示是三个反比例函数y=,y=,y=的图象,由此观察k1、k2、k3的大小关系是 .(用“<”连接)
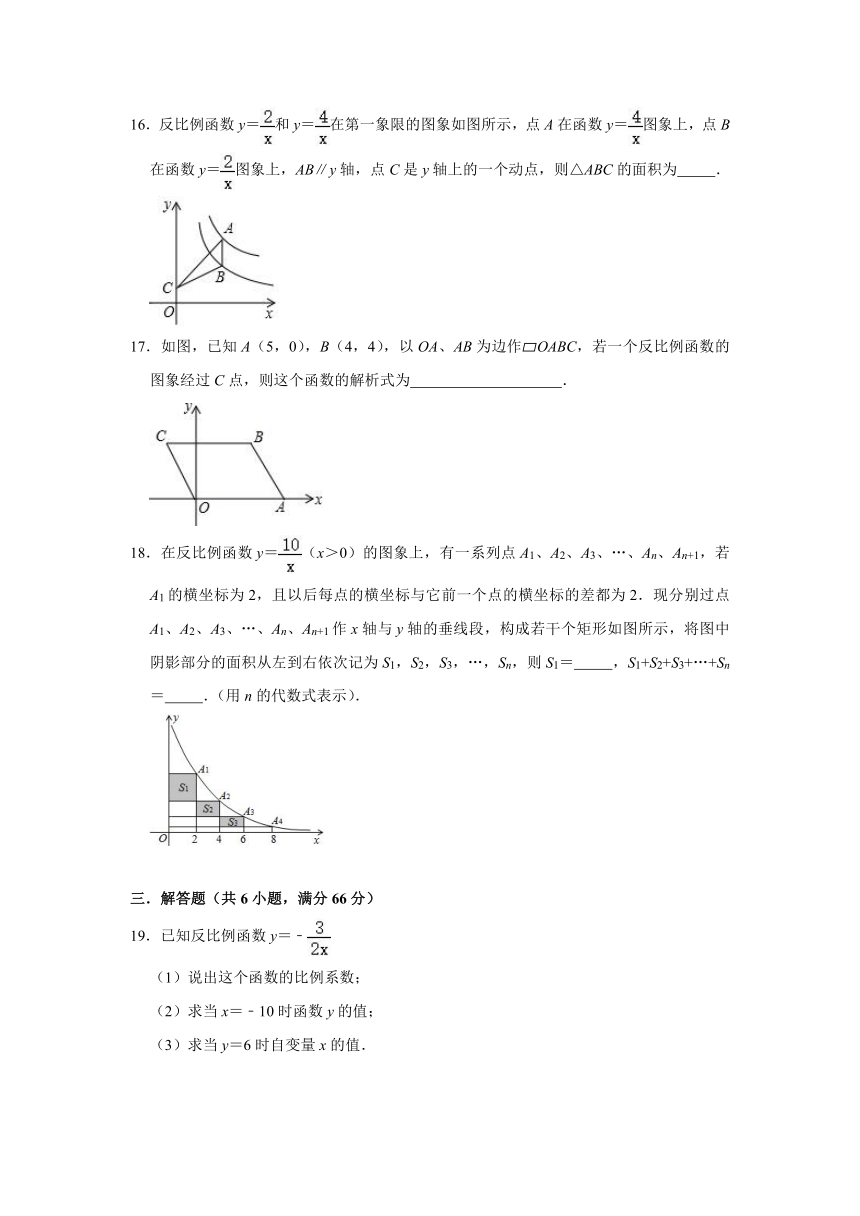
16.反比例函数y=和y=在第一象限的图象如图所示,点A在函数y=图象上,点B在函数y=图象上,AB∥y轴,点C是y轴上的一个动点,则△ABC的面积为 .
17.如图,已知A(5,0),B(4,4),以OA、AB为边作 OABC,若一个反比例函数的图象经过C点,则这个函数的解析式为 .
18.在反比例函数y=(x>0)的图象上,有一系列点A1、A2、A3、…、An、An+1,若A1的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2.现分别过点A1、A2、A3、…、An、An+1作x轴与y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1= ,S1+S2+S3+…+Sn= .(用n的代数式表示).
三.解答题(共6小题,满分66分)
19.已知反比例函数y=﹣
(1)说出这个函数的比例系数;
(2)求当x=﹣10时函数y的值;
(3)求当y=6时自变量x的值.
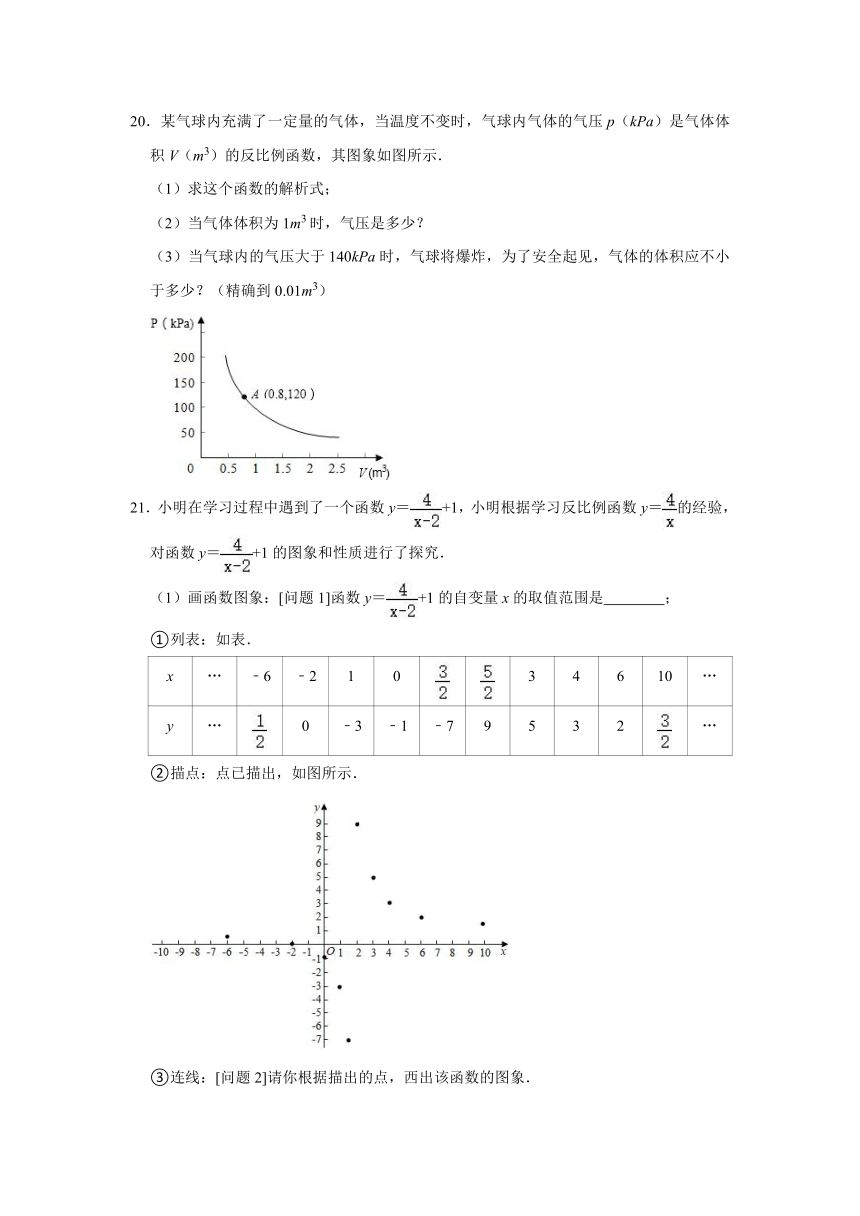
20.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这个函数的解析式;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到0.01m3)
21.小明在学习过程中遇到了一个函数y=+1,小明根据学习反比例函数y=的经验,对函数y=+1的图象和性质进行了探究.
(1)画函数图象:[问题1]函数y=+1的自变量x的取值范围是 ;
①列表:如表.
x … ﹣6 ﹣2 1 0 3 4 6 10 …
y … 0 ﹣3 ﹣1 ﹣7 9 5 3 2 …
②描点:点已描出,如图所示.
③连线:[问题2]请你根据描出的点,西出该函数的图象.
(2)探究性质:根据反比例函数y=的图象和性质,结合画出的函数y=+1图象,回答下列问题:
[问题3]①该函数的图象是具有轴对称性和中心对称性,其对称中心的坐标是 ;
[问题4]②该函数图象可以看成是由y=的图象平移得到的,其平移方式为 ;
[问题5]③结合函数图象,请直接写出+1≥﹣1时x的取值范围 .
22.已知A(a,﹣2a)、B(﹣2,a)两点是反比例函数y=与一次函数y=kx+b图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△ABO的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
23.为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
24.如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=相交于A(﹣2,3),B(m,﹣2)两点.
(1)求y1,y2对应的函数表达式;
(2)过点B作BP∥x轴交y轴于点P,求△ABP的面积;
(3)根据函数图象,直接写出关于x的不等式k1x+b<的解集.
参考答案
一.选择题(共10小题,满分30分)
1.解:A、y=4x是正比例函数;
B、=3,可以化为y=3x,是正比例函数;
C、y=﹣是反比例函数;
D、y=x2﹣1是二次函数;
故选:C.
2.解:由于以80千米/时的平均速度用了6小时到达目的地,那么路程为80×6=480千米,
∴汽车的速度v(千米/时)与时间t(小时)的函数关系为v=.
故选:A.
3.解:∵函数y=kx中y随x的增大而减小,
∴k<0,
∴函数y=kx的图象经过二、四象限,故可排除A、B;
∵k<0,
∴函数y=的图象在二、四象限,故C错误,D正确.
故选:D.
4.解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:πr2=10π.
解得:r=2.
∵点P(﹣2a,a)是反比例函数y=(k>0)与⊙O的一个交点.
∴﹣2a2=k且=r.
∴a2=8.
∴k=﹣2×8=﹣16,
则反比例函数的解析式是:y=﹣.
故选:D.
5.解:∵反比例函数的图象在第一、第三象限,
∴1﹣m>0,
∴m<1,
符合条件的答案只有A,
故选:A.
6.解:由题意得,点C的坐标(t,﹣),
点B的坐标(t,),
BC=+,
则(+)×t=3,
解得k=5,
故选:D.
7.解:∵一次函数y=x+4中,当x=0时,y=0+4=4,
∴A(0,4),
∴OA=4;
∵当y=0时,0=x+4,
∴x=﹣3,
∴B(﹣3,0),
∴OB=3;
过点C作CE⊥x轴于E,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵∠CBE+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠CBE=∠BAO.
在△AOB和△BEC中,
,
∴△AOB≌△BEC(AAS),
∴BE=AO=4,CE=OB=3,
∴OE=3+4=7,
∴C点坐标为(﹣7,3),
∵点C在反比例函数y=(x<0)图象上,
∴k=﹣7×3=﹣21.
故选:D.
8.解:过点B作BD⊥x轴于点D,
∵∠ACO+∠BCD=90°,
∠OAC+∠ACO=90°,
∴∠OAC=∠BCD,
在△ACO与△BCD中,
,
∴△ACO≌△CBD(AAS),
∴OC=BD,OA=CD,
∵A(0,2),C(1,0),
∴OD=3,BD=1,
∴B(3,1),
∴设反比例函数的解析式为y=(k≠0),
将B(3,1)代入y=,
∴1=,
∴k=3,
∴该反比例函数的解析式为y=,
故选:A.
9.解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项不正确,符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x﹣70,
故y=200时,200=30x﹣70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
10.解:设函数解析式为T=,
∵经过点(1,3),
∴k=1×3=3,
∴函数解析式为T=,
当T≤2℃时,t≥h,
故选:C.
二.填空题(共8小题,满分24分)
11.解:因为是反比例函数,
所以x的指数m2﹣5=﹣1,
即m2=4,解得:m=2或﹣2;
又m﹣2≠0,
所以m≠2,即m=﹣2.
故答案为:﹣2.
12.解:由题意得:Sh=5×104,
∴S=,
故答案为:S=.
13.解:∵反比例函数y=(x<0)的图象在第二象限,
∴m+2<0,
∴m<﹣2.
故答案为:m<﹣2.
14.解:∵直线y=k1x+b与双曲线y=在同一平面直角坐标系中的图象的交点的横坐标是﹣2和3,
∴关于x的不等式>k1x+b的解集是x<﹣2或0<x<3,
故答案为:x<﹣2或0<x<3.
15.解:根据图象可知|k|越大,开口越小,
则k1<0,k2>k3>0,
所以k1,k2,k3的大小关系是k1<k3<k2.
故答案为:k1<k3<k2.
16.解:连接OA、OB,延长AB,交x轴于D,如图,
∵AB∥y轴,
∴AD⊥x轴,OC∥AB,
∴S△OAB=S△ABC,
而S△OAD=×4=2,S△OBD=×2=1,
∴S△OAB=S△OAD﹣S△OBD=1,
∴S△ABC=1,
故答案为1.
17.解:∵A(5,0),B(4,4),以OA、AB为边作 OABC,
∴BC=AO=5,BE=4,EO=4,
∴EC=1,故C(﹣1,4),
若一个反比例函数的图象经过C点,则这个函数的解析式为:y=﹣.
故答案为:y=﹣.
18.解:∵点A1、A2、A3、…、An、An+1在反比例函数y=(x>0)的图象上,且每点的横坐标与它前一个点的横坐标的差都为2,
又点A1的横坐标为2,
∴A1(2,5),A2(4,)
∴S1=2×(5﹣)=5;
由题图象知,An(2n,),An+1(2n+2,),
∴S2=2×()=,
∴图中阴影部分的面积知:Sn=2×()=,(n=1,2,3,…)
∵=,
∴S1+S2+S3+…+Sn=10(++…+)=10(1)=.
故答案为:5,.
三.解答题(共6小题,满分66分)
19.解:(1)原式=,比例系数为﹣;
(2)当x=﹣10时,原式=﹣=;
(3)当y=6时,﹣=6,解得,x=﹣.
20.解:(1)设,
由题意知,
所以k=96,
故;
(2)当v=1m3时,;
(3)当p=140kPa时,.
所以为了安全起见,气体的体积应不少于0.69m3.
21.解:(1)函数y=+1的自变量x的取值范围是:x≠2,
故答案为:x≠2;
如图所示,
(2)根据反比例函数y=的图象和性质,结合画出的函数y=+1图象可知:
①该函数的图象是具有轴对称性和中心对称性,其对称中心的坐标是 (2,1);
②该函数图象可以看成是由y=的图象平移得到的,其平移方式为:向右平移2个单位,再向上平移1个单位;
③结合函数图象,+1≥﹣1时x的取值范围是x≤0或x>2.
故答案为(2,1);向右平移2个单位,再向上平移1个单位;x≤0或x>2.
22.解:(1)∵A(a,﹣2a)、B(﹣2,a)两点在反比例函数y=的图象上,
∴m=﹣2a a=﹣2a,
解得a=1,m=﹣2,
∴A(1,﹣2),B(﹣2,1),反比例函数的解析式为y=﹣.
将点A(1,﹣2)、点B(﹣2,1)代入到y=kx+b中,
得:,解得:,
∴一次函数的解析式为y=﹣x﹣1.
(2)在直线y=﹣x﹣1中,令y=0,则﹣x﹣1=0,解得x=﹣1,
∴C(﹣1,0),
∴S△AOB=S△AOC+S△BOC=×1×2+×1=;
(3)观察函数图象,发现:
当x<﹣2或0<x<1时,反比例函数图象在一次函数图象的下方,
∴不等式kx+b﹣>0的解集为x<﹣2或0<x<1.
23.解:(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0),
代入(8,6)得6=8k1,
∴k1=,
设药物燃烧后y关于x的函数关系式为y=(k2>0),
代入(8,6)得
6=,
∴k2=48,
∴药物燃烧时y关于x的函数关系式为(0≤x≤8)药物燃烧后y关于x的函数关系式为:
(x>8),
∴;
(2)把y=3代入,得:x=4,
把y=3代入,得:x=16,
∵16﹣4=12,
所以这次消毒是有效的.
24.解:(1)∵直线y1=k1x+b与双曲线相交于A(﹣2,3),B(m,﹣2)两点,
∴,解得:k2=﹣6,
∴双曲线的表达式为:,
∴把B(m,﹣2)代入,得:,解得:m=3,
∴B(3,﹣2),
把A(﹣2,3)和B(3,﹣2)代入y1=k1x+b得:,
解得:,
∴直线的表达式为:y1=﹣x+1;
(2)过点A作AD⊥BP,交BP的延长线于点D,如图
∵BP∥x轴,
∴AD⊥x轴,BP⊥y轴,
∵A(﹣2,3),B(3,﹣2),
∴BP=3,AD=3﹣(﹣2)=5,
∴;
(3)的解集,则是双曲线的图象在一次函数的图象的上方对应的x的取值,
故其解集为:﹣2<x<0或x>3.
一.选择题(共10小题,满分30分)
1.下列关系式中,y是x的反比例函数的是( )
A.y=4x B.=3 C.y=﹣ D.y=x2﹣1
2.一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
3.已知函数y=kx中y随x的增大而减小,那么它和函数y=在同一平面直角坐标系内的大致图象可能是( )
A.B.C.D.
4.如图,点P(﹣2a,a)是反比例函数y=与⊙O的一个交点,图中阴影部分的面积为10π,则该反比例函数的表达式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=﹣
5.反比例函数的图象在第一、第三象限,则m可能取的一个值为( )
A.0 B.1 C.2 D.3
6.如图,直线x=t(t>0)与反比例函数y=(x>0)、y=(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )
A.2 B.3 C.4 D.5
7.如图,在平面直角坐标系中,一次函数y=x+4的图象与x轴、y轴分别相交于点B,点A,以线段AB为边作正方形ABCD,且点C在反比例函数y=(x<0)图象上,则k的值为( )
A.﹣12 B.﹣42 C.42 D.﹣21
8.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标(0,2),顶点B恰好落在第一象限的双曲线上,则该反比例函数的解析式为( )
A. B. C. D.
9.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2021年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元 B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元D.9月份该厂利润达到200万元
10.如图,曲线表示温度T(℃)与时间t(h)之间的函数关系,它是一个反比例函数的图象的一支.当温度T≤2℃时,时间t应( )
A.不小于h B.不大于h C.不小于h D.不大于h
二.填空题(共8小题,满分24分)
11.已知:是反比例函数,则m= .
12.某厂计划建造一个容积为5×104m3的长方体蓄水池,则蓄水池的底面积S(m2)与其深度h(m)的函数关系式是 .
13.反比例函数y=(x<0)的图象如图所示,则m的取值范围为 .
14.直线y=k1x+b与双曲线y=在同一平面直角坐标系中的图象如图所示,则关于x的不等式>k1x+b的解集为 .
15.如图所示是三个反比例函数y=,y=,y=的图象,由此观察k1、k2、k3的大小关系是 .(用“<”连接)
16.反比例函数y=和y=在第一象限的图象如图所示,点A在函数y=图象上,点B在函数y=图象上,AB∥y轴,点C是y轴上的一个动点,则△ABC的面积为 .
17.如图,已知A(5,0),B(4,4),以OA、AB为边作 OABC,若一个反比例函数的图象经过C点,则这个函数的解析式为 .
18.在反比例函数y=(x>0)的图象上,有一系列点A1、A2、A3、…、An、An+1,若A1的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2.现分别过点A1、A2、A3、…、An、An+1作x轴与y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1= ,S1+S2+S3+…+Sn= .(用n的代数式表示).
三.解答题(共6小题,满分66分)
19.已知反比例函数y=﹣
(1)说出这个函数的比例系数;
(2)求当x=﹣10时函数y的值;
(3)求当y=6时自变量x的值.
20.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这个函数的解析式;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到0.01m3)
21.小明在学习过程中遇到了一个函数y=+1,小明根据学习反比例函数y=的经验,对函数y=+1的图象和性质进行了探究.
(1)画函数图象:[问题1]函数y=+1的自变量x的取值范围是 ;
①列表:如表.
x … ﹣6 ﹣2 1 0 3 4 6 10 …
y … 0 ﹣3 ﹣1 ﹣7 9 5 3 2 …
②描点:点已描出,如图所示.
③连线:[问题2]请你根据描出的点,西出该函数的图象.
(2)探究性质:根据反比例函数y=的图象和性质,结合画出的函数y=+1图象,回答下列问题:
[问题3]①该函数的图象是具有轴对称性和中心对称性,其对称中心的坐标是 ;
[问题4]②该函数图象可以看成是由y=的图象平移得到的,其平移方式为 ;
[问题5]③结合函数图象,请直接写出+1≥﹣1时x的取值范围 .
22.已知A(a,﹣2a)、B(﹣2,a)两点是反比例函数y=与一次函数y=kx+b图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△ABO的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
23.为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
24.如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=相交于A(﹣2,3),B(m,﹣2)两点.
(1)求y1,y2对应的函数表达式;
(2)过点B作BP∥x轴交y轴于点P,求△ABP的面积;
(3)根据函数图象,直接写出关于x的不等式k1x+b<的解集.
参考答案
一.选择题(共10小题,满分30分)
1.解:A、y=4x是正比例函数;
B、=3,可以化为y=3x,是正比例函数;
C、y=﹣是反比例函数;
D、y=x2﹣1是二次函数;
故选:C.
2.解:由于以80千米/时的平均速度用了6小时到达目的地,那么路程为80×6=480千米,
∴汽车的速度v(千米/时)与时间t(小时)的函数关系为v=.
故选:A.
3.解:∵函数y=kx中y随x的增大而减小,
∴k<0,
∴函数y=kx的图象经过二、四象限,故可排除A、B;
∵k<0,
∴函数y=的图象在二、四象限,故C错误,D正确.
故选:D.
4.解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:πr2=10π.
解得:r=2.
∵点P(﹣2a,a)是反比例函数y=(k>0)与⊙O的一个交点.
∴﹣2a2=k且=r.
∴a2=8.
∴k=﹣2×8=﹣16,
则反比例函数的解析式是:y=﹣.
故选:D.
5.解:∵反比例函数的图象在第一、第三象限,
∴1﹣m>0,
∴m<1,
符合条件的答案只有A,
故选:A.
6.解:由题意得,点C的坐标(t,﹣),
点B的坐标(t,),
BC=+,
则(+)×t=3,
解得k=5,
故选:D.
7.解:∵一次函数y=x+4中,当x=0时,y=0+4=4,
∴A(0,4),
∴OA=4;
∵当y=0时,0=x+4,
∴x=﹣3,
∴B(﹣3,0),
∴OB=3;
过点C作CE⊥x轴于E,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵∠CBE+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠CBE=∠BAO.
在△AOB和△BEC中,
,
∴△AOB≌△BEC(AAS),
∴BE=AO=4,CE=OB=3,
∴OE=3+4=7,
∴C点坐标为(﹣7,3),
∵点C在反比例函数y=(x<0)图象上,
∴k=﹣7×3=﹣21.
故选:D.
8.解:过点B作BD⊥x轴于点D,
∵∠ACO+∠BCD=90°,
∠OAC+∠ACO=90°,
∴∠OAC=∠BCD,
在△ACO与△BCD中,
,
∴△ACO≌△CBD(AAS),
∴OC=BD,OA=CD,
∵A(0,2),C(1,0),
∴OD=3,BD=1,
∴B(3,1),
∴设反比例函数的解析式为y=(k≠0),
将B(3,1)代入y=,
∴1=,
∴k=3,
∴该反比例函数的解析式为y=,
故选:A.
9.解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项不正确,符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x﹣70,
故y=200时,200=30x﹣70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
10.解:设函数解析式为T=,
∵经过点(1,3),
∴k=1×3=3,
∴函数解析式为T=,
当T≤2℃时,t≥h,
故选:C.
二.填空题(共8小题,满分24分)
11.解:因为是反比例函数,
所以x的指数m2﹣5=﹣1,
即m2=4,解得:m=2或﹣2;
又m﹣2≠0,
所以m≠2,即m=﹣2.
故答案为:﹣2.
12.解:由题意得:Sh=5×104,
∴S=,
故答案为:S=.
13.解:∵反比例函数y=(x<0)的图象在第二象限,
∴m+2<0,
∴m<﹣2.
故答案为:m<﹣2.
14.解:∵直线y=k1x+b与双曲线y=在同一平面直角坐标系中的图象的交点的横坐标是﹣2和3,
∴关于x的不等式>k1x+b的解集是x<﹣2或0<x<3,
故答案为:x<﹣2或0<x<3.
15.解:根据图象可知|k|越大,开口越小,
则k1<0,k2>k3>0,
所以k1,k2,k3的大小关系是k1<k3<k2.
故答案为:k1<k3<k2.
16.解:连接OA、OB,延长AB,交x轴于D,如图,
∵AB∥y轴,
∴AD⊥x轴,OC∥AB,
∴S△OAB=S△ABC,
而S△OAD=×4=2,S△OBD=×2=1,
∴S△OAB=S△OAD﹣S△OBD=1,
∴S△ABC=1,
故答案为1.
17.解:∵A(5,0),B(4,4),以OA、AB为边作 OABC,
∴BC=AO=5,BE=4,EO=4,
∴EC=1,故C(﹣1,4),
若一个反比例函数的图象经过C点,则这个函数的解析式为:y=﹣.
故答案为:y=﹣.
18.解:∵点A1、A2、A3、…、An、An+1在反比例函数y=(x>0)的图象上,且每点的横坐标与它前一个点的横坐标的差都为2,
又点A1的横坐标为2,
∴A1(2,5),A2(4,)
∴S1=2×(5﹣)=5;
由题图象知,An(2n,),An+1(2n+2,),
∴S2=2×()=,
∴图中阴影部分的面积知:Sn=2×()=,(n=1,2,3,…)
∵=,
∴S1+S2+S3+…+Sn=10(++…+)=10(1)=.
故答案为:5,.
三.解答题(共6小题,满分66分)
19.解:(1)原式=,比例系数为﹣;
(2)当x=﹣10时,原式=﹣=;
(3)当y=6时,﹣=6,解得,x=﹣.
20.解:(1)设,
由题意知,
所以k=96,
故;
(2)当v=1m3时,;
(3)当p=140kPa时,.
所以为了安全起见,气体的体积应不少于0.69m3.
21.解:(1)函数y=+1的自变量x的取值范围是:x≠2,
故答案为:x≠2;
如图所示,
(2)根据反比例函数y=的图象和性质,结合画出的函数y=+1图象可知:
①该函数的图象是具有轴对称性和中心对称性,其对称中心的坐标是 (2,1);
②该函数图象可以看成是由y=的图象平移得到的,其平移方式为:向右平移2个单位,再向上平移1个单位;
③结合函数图象,+1≥﹣1时x的取值范围是x≤0或x>2.
故答案为(2,1);向右平移2个单位,再向上平移1个单位;x≤0或x>2.
22.解:(1)∵A(a,﹣2a)、B(﹣2,a)两点在反比例函数y=的图象上,
∴m=﹣2a a=﹣2a,
解得a=1,m=﹣2,
∴A(1,﹣2),B(﹣2,1),反比例函数的解析式为y=﹣.
将点A(1,﹣2)、点B(﹣2,1)代入到y=kx+b中,
得:,解得:,
∴一次函数的解析式为y=﹣x﹣1.
(2)在直线y=﹣x﹣1中,令y=0,则﹣x﹣1=0,解得x=﹣1,
∴C(﹣1,0),
∴S△AOB=S△AOC+S△BOC=×1×2+×1=;
(3)观察函数图象,发现:
当x<﹣2或0<x<1时,反比例函数图象在一次函数图象的下方,
∴不等式kx+b﹣>0的解集为x<﹣2或0<x<1.
23.解:(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0),
代入(8,6)得6=8k1,
∴k1=,
设药物燃烧后y关于x的函数关系式为y=(k2>0),
代入(8,6)得
6=,
∴k2=48,
∴药物燃烧时y关于x的函数关系式为(0≤x≤8)药物燃烧后y关于x的函数关系式为:
(x>8),
∴;
(2)把y=3代入,得:x=4,
把y=3代入,得:x=16,
∵16﹣4=12,
所以这次消毒是有效的.
24.解:(1)∵直线y1=k1x+b与双曲线相交于A(﹣2,3),B(m,﹣2)两点,
∴,解得:k2=﹣6,
∴双曲线的表达式为:,
∴把B(m,﹣2)代入,得:,解得:m=3,
∴B(3,﹣2),
把A(﹣2,3)和B(3,﹣2)代入y1=k1x+b得:,
解得:,
∴直线的表达式为:y1=﹣x+1;
(2)过点A作AD⊥BP,交BP的延长线于点D,如图
∵BP∥x轴,
∴AD⊥x轴,BP⊥y轴,
∵A(﹣2,3),B(3,﹣2),
∴BP=3,AD=3﹣(﹣2)=5,
∴;
(3)的解集,则是双曲线的图象在一次函数的图象的上方对应的x的取值,
故其解集为:﹣2<x<0或x>3.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
