2021-2022学年北师大版九年级下册数学第三章圆综合压轴题(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级下册数学第三章圆综合压轴题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 14:29:58 | ||
图片预览



文档简介
北师大版九年级下数学圆综合压轴题(一)
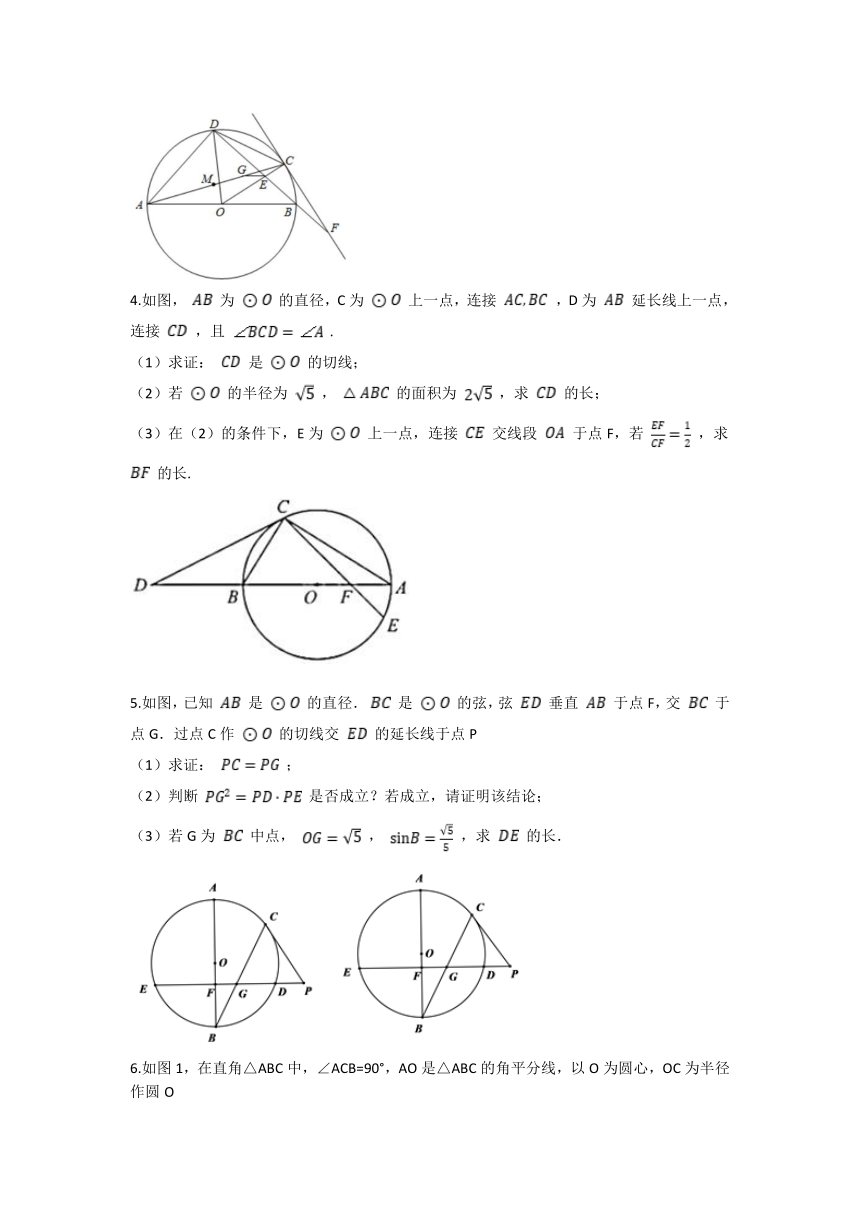
1.如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1).判断直线CD与⊙O的位置关系,并说明理由;
(2).若tan∠ADC= ,AC=2,求⊙O的半径;
(3).如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.
2.如图,已知 , 是 的直径, , 与 的边 , 分别交于点 , ,连接 并延长,与 的延长线交于点 , .
(1).求证: 是 的切线;
(2).若 ,求 的值;
(3).在(2)的条件下,若 的平分线 交 于点 ,连接 交 于点 ,求 的值.
3.如图所示, 是 的直径,点 、 是 上不同的两点,直线 交线段 于点 ,交过点 的直线 于点 ,若 ,且 .
(1)求证:直线 是 的切线;
(2)连接 、 、 、 ,若 .
①求证: ;
②过点 作 ,交线段 于点 ,点 为线段 的中点,若 ,求线段 的长度.
4.如图, 为 的直径,C为 上一点,连接 ,D为 延长线上一点,连接 ,且 .
(1)求证: 是 的切线;
(2)若 的半径为 , 的面积为 ,求 的长;
(3)在(2)的条件下,E为 上一点,连接 交线段 于点F,若 ,求 的长.
5.如图,已知 是 的直径. 是 的弦,弦 垂直 于点F,交 于点G.过点C作 的切线交 的延长线于点P
(1)求证: ;
(2)判断 是否成立?若成立,请证明该结论;
(3)若G为 中点, , ,求 的长.
6.如图1,在直角△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作圆O
(1).求证:AB是⊙O的切线;
(2).已知AO交圆O于点E,延长AO交圆O于点D,tan∠D= ,求 的值;
(3).如图2,在(2)条件下,若AB与⊙O的切点为点F,连接CF交AD于点G,设⊙O的半径为3,求CF的长.
7.如图,在 中, , 是边 上一动点,且不与 , 两点重合,连结 ,过点 作 交边 于点 , 的外接圆交边 于另一点 ,连结 .
(1).求证: .
(2).当 , 时.
①若 ,求 的长.
②当线段 , , 中有两条相等时,求出所有符合条件的 的值.
(3).若 平分 , , ,则 .
8.如图,BC是⊙O的直径,AD是⊙O的弦,AD交BC于点E,连接AB,CD,过点E作EF⊥AB,垂足为F,∠AEF=∠D.
(1).求证:AD⊥BC;
(2).点G在BC的延长线上,连接AG,∠DAG=2∠D.
①求证:AG与⊙O相切;
②当 ,CE=4时,直接写出CG的长.
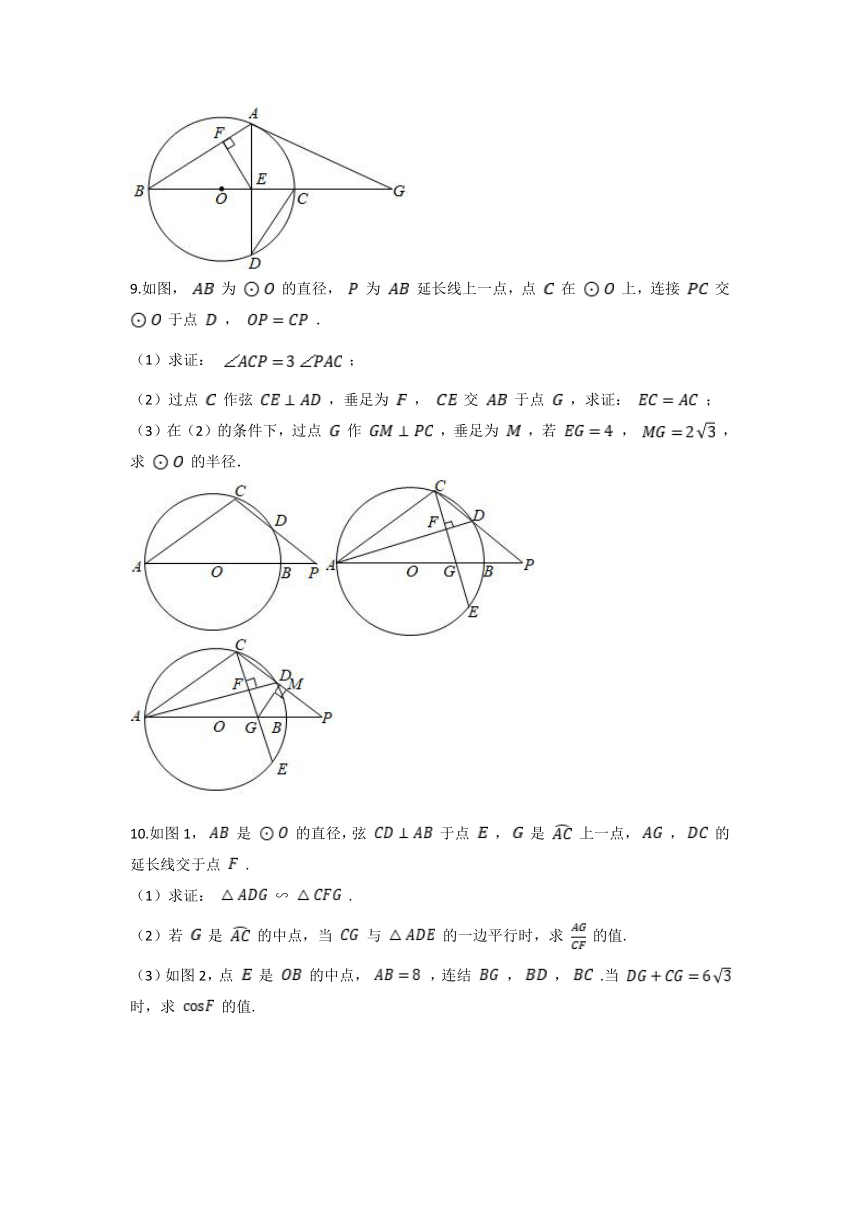
9.如图, 为 的直径, 为 延长线上一点,点 在 上,连接 交 于点 , .
(1)求证: ;
(2)过点 作弦 ,垂足为 , 交 于点 ,求证: ;
(3)在(2)的条件下,过点 作 ,垂足为 ,若 , ,求 的半径.
10.如图1, 是 的直径,弦 于点 , 是 上一点, , 的延长线交于点 .
(1)求证: ∽ .
(2)若 是 的中点,当 与 的一边平行时,求 的值.
(3)如图2,点 是 的中点, ,连结 , , .当 时,求 的值.
11.如图. 为半圆 的直径,点 为半圆 上一点,过点 作半圆 的切线 交 的延长线于点 .过点 作 于点 ,交半圆 于点 ,过点 作 于点 ,连接 , , .
(1).求证: ;
(2).填空:①连接 ,当 的度数为 时,四边形 为菱形;
②若 . ,则 的长为 .
12.如图, 为 直径,弦 交 于点E,G为 上一点,连接 交 于点F,交 于点H,连接 ,且 .
(1)如图1,求证: ;
(2)如图2,若 ,求证: ;
(3)如图3,在(2)的条件下,若 ,求 的半径.
13.如图,在 中, , 的垂直平分线分别与 , 及 的延长线相交于点D , E , F , 且 . 是 的外接圆, 的平分线交 于点G , 交 于点H , 连接 、 .
(1)求证: ;
(2)试判断 与 的位置关系,并说明理由;
(3)若 ,求 的值.
14.如图,四边形 内接于 , 为 的直径, 是 的切线, 交 的延长线于点 ,过点 作 于点 ,连接 交 于点 .
(1)求证: ;
(2)若 , ,求 的半径;
(3)在(2)的条件下,求四边形 的面积.
15.如图, 与 的边 相切于点C , 与 分别交于点D , E , 是 的直径,过点A作 交 于M , N两点(点M在线段 上).
(1)求证:直线 与 相切;
(2)求证: ;
(3)若 ,求 的长.
16.如图, 为 的切线, 为切点,过 作 的垂线 ,垂足为点 ,交 于点 .连接 并延长交 于点 ,交 的延长线于点 .
(1)求证: 为 的切线;
(2)若 , ,求 的半径;
(3)若 ,求 的值.
17.如图,在 中, , , 是 的中点,以 为直径的⊙ 与 的三边分别交于点 、 、 ,连接 、 , 与 交于点 ﹒
(1)求证: ;
(2)若 , ,求⊙ 的直径 的长;
(3)设 , ,求 与 之间的函数关系式﹒
18.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是 上一点,AG,DC的延长线交于点F,连接AD,GD,GC.
(1)求证:∠CGF=∠AGD.
(2)已知∠DGF=120°,AB=4.
①求CD的长.
②若 ,求△ADG与△AFD的面积之比.
19.(提出问题)
如图1,直径 垂直弦 于点E, , ,点P是 延长线上异于点D的一个动点,连结 交 于点Q,连结 交 于点F,则点F的位置随着点P位置的改变而改变.
(1)(特殊位置探究)
当 时,求 和线段 的长;
(2)(一般规律探究)
如图2,连结 , .在点P运动过程中,设 , .
①求证: ;
②求y与x之间的函数关系式:
(3)(解决问题)
当 时,求 和 的面积之比.(直接写出答案)
20.如图,在 中,半径 直径 与 相切于点 连接 交 于点 交 于点 ,连接 并延长交 于点 ,连接 .
(1)求证: ;
(2)若
①求证:四边形 是平行四边形;
②连接 ,当 的半径为 时,求 的长.
21.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,D为圆上一点,且B,D两点位于AC异侧,连接BD,交AC于E,点F为BD延长线上一点,连接AF,使得∠DAF=∠ABD.
(1)求证:AF为⊙O的切线;
(2)当点D为EF的中点时,求证:AD2=AO AE;
(3)在(2)的条件下,若sin∠BAC= ,AF=2 ,求BF的长.
答案解析部分
1.【答案】 (1)解:CD与⊙O相切,理由:
如图1,连接OD,
∵OB=OD,
∴∠ODB=∠CBD,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB为⊙O的直径,
∴∠ADB=∠ADO+∠ODB=90°,
∴∠CDA+∠ADO=90°,
∴∠CDO=90°,
∴OD⊥CD,
∴CD与⊙O相切
(2)解:由(1)知,∠CBD=∠ADC,
∵tan∠ADC= ,
∴tan∠CBD= ,
在Rt△ADB中,tan∠CBD= = ,
∵∠C=∠C,∠ADC=∠CBD,
∴△CAD∽△CDB,
∴ ,
∴CD=2CA=4,
∴CB=2CD=8,
∴AB=CB CA=8 2=6,
∴OA=OB= AB=3
(3)解:如图2,连接OE,过点E作EG⊥BD于G,
∵DE平分∠ADB,
∴∠ADE=∠BDE=45°,
∴∠BOE=2∠BDE=90°,
∴BE= =3 ,
在Rt△ABD中,AD2+BD2=AB2=62 ,
∵ = ,
∴AD= ,BD= ,
∵EG⊥BD,∠BDE=45°,
∴∠DEG=∠BDE=45°,
∴DG=EG,
设DG=EG=x,则BG=BD DG= x,
在Rt△BEG中,EG2+BG2=BE2=(3 )2=18,
∴x2+( x)2=18,
∴x= 或x= (舍),
∴EG= ,
∴sin∠DBE=
【解析】【分析】(1)连接OD,由等腰三角形的性质结合已知条件可得∠CDA=∠ODB,由圆周角定理可得∠ADB=90°,推出∠CDO=90°,据此判断;
(2)由(1)知,∠CBD=∠ADC,则tan∠ADC=tan∠CBD= , 证明△CAD∽△CDB,由相似三角形的性质可得CD、CB的值,进而求出AB、OA的值;
(3)连接OE,过点E作EG⊥BD于G,由角平分线的概念可得∠ADE=∠BDE=45°,则∠BOE=90°,由勾股定理求出BE、AD、BD的值,设DG=EG=x,则BG= x,然后在Rt△BEG中,应用勾股定理求出x的值,进而得到sin∠DBE的值.
2.【答案】 (1)证明:如图,连接DF,
∵ 是 的直径,
∴ .
∴DF∥AE.
∵四边形ABCD是平行四边形,
∴AE∥OC.
∴DF∥OC.
∴ .
∵ ,
∴ .
∵ ,
∴ .
∵ ,
∴ .
∴ .
∴ .
∴ 是 的切线
(2)解:∵ ,
∴ .
∴ .
∴ .
∴ .
∵ ,
∴ .
设 ,则 .
由勾股定理得 ,
即 ,
解得 , (不合题意,舍去).
∴ .
∵ ,
∴
(3)解:连接MN,并延长CO与AF, 分别相交于点P,点Q,连接AQ,
∵四边形ABCD是平行四边形,
∴ , ,AB∥OC.
∴ ,
∵ 平分 ,
∴ .
∴ .
∴ .
∵
∴ .
∵ ,
∴ .
∴ .
∴ .
∴ .
∵AB∥OC,
∴ .
∴ .
∵ ,
∴ .
在Rt△APO中,由勾股定理得 .
∴ .
在Rt△APH中,由勾股定理得 .
∵ ,
∴ .
∵ ,
∴ .
∴ .
∴
【解析】【分析】(1)连接DF,利用平行线的判定定理可证得DF∥AE,利用平行四边形的性质可证得AE∥OC,由此可证得DF∥OC;再利用平行线的性质及等腰三角形的性质可推出∠FAD=∠OCD,根据∠FDA+∠FAD=90°,可得到∠ODC=90°;然后利用切线的判定定理可证得结论.
(2)利用余角的性质可证得∠FDG=∠FAD,由此可推出△FDG∽△FAD,利用相似三角形的性质,可证得FD2=FG·FA,设DF=x,可表示出AF的长,利用勾股定理建立关于x的方程,解方程求出x的值,可求出DF的长;再利用锐角三角函数的定义及∠AEF=∠ADF,可求出cos∠AEF的值.
(3)连接MN,并延长CO与AF, 分别相交于点P,点Q,连接AQ,利用平行四边形的性质和平行线的性质可证得OC=AB,AO=BC,∠CHB=∠ABH,再利用角平分线的定义去证明∠CHB=∠BCH,由此可求出CH的长;然后解直角三角形求出OC,AB的长,由此可求出MH的长及HQ的长,可推出HQ=AB;然后求出AP的长,利用勾股定理在Rt△APO中求出OP的长,可得到PH的长;在Rt△APH中,利用勾股定理求出AH的长;利用有两组对应角相等的两三角形相似,可证得△MHN∽△AHQ,利用相似三角形的性质可求出AB与NH的比值.
3.【答案】 (1)证明:因为 ,且 ,
∴ ,
∴ ,
∴ ,
∴直线 是 的切线
(2)解:①∵ ,
又∵ ,
∴ ,
∵ ,
∴. ;
②∵ ,
∴ ,
设圆的半径为r,
∵ , ,
∴ ,
∴ ;
∵点 为线段 的中点,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴线段 的长度为1
【解析】【分析】(1)由题意用勾股定理的逆定理易证∠ECF=90°,然后根据圆的切线的判定可求解;
(2)①证明∠DAC=∠EOB,∠DCA=∠EBO,根据有两个角对应相等的两个三角形相似可求解;
②由①中知:△ACD∽△OBE,再由相似三角形的性质可得比例式 , 结合已知可求得AC的值,再由平行线分线段成比例定理"两条直线被一组平行线所截,截得的对应线段的长度成比例"可得比例式 , 于是可求出CG的值,再根据线段的构成MG=CM-CG可求解.
4.【答案】 (1)证明:连接 ,
∵AB为⊙O直径,
∴∠ACB=90°,
∴∠CAB+∠CBO=90°,
又∵OB=OC,
∴∠CBO=∠BCO,
∴∠CAB+∠BCO=90°
∵∠BCD=∠A,
∴∠BCD+∠BCO=90°,
∴OC⊥CD
∴CD为⊙O切线
(2)解:过点C作 于点M,
∵ 的半径为 ,
∴AB= ,
∵ 的面积为 ,
∴CM=2,
在Rt△CMO中,CO= ,CM=2,
∴OM=1,
由(1)得∠OCD=∠CMO=90°,
∵∠COM=∠COD,
∴△COM∽△DOC,
∴ ,
∴ ,
∴
(3)解:过点E作 于点N,连接 ,
∵ , ,
∴△FCM∽△FEN,
∴ ,
由(2)得CM=2,OM=1,
∴EN=OM=1,
∵OC=OE,
∴Rt△COM≌Rt△OEN,
∴ON=CM=2,
∴MN=3,
∵ ,
∴FM=2,
∵OM=1,
∴OF=1,
∵BF=OB+OF,
∴
【解析】∴MN=3,
∵ ,
∴FM=2,
∵OM=1,
∴OF=1,
∵BF=OB+OF,
∴
【分析】(1)连接OC,由直径所对的圆周角是直角可得∠ACB=∠A+∠ABC=90°,由等边对等角得∠ABC=∠BCO,结合已知可得∠ACB=90°,然后根据圆的切线的判定可求解;
(2)过C作CM⊥AB于M,由△ABC的面积为2=AB×CM可求得CM的值,根据有两个角对应相等的两个三角形全等可得△COM∽△DOC,可得比例式 , 则CD的值可求解;
(3) 过点E作于点N,连接OE,由CM⊥AB,EN⊥AB,可得△FCM∽△FEN,于是可得比例式 , 由(2)得CM=2,OM=1,于是可得EN=OM,结合已知OC=OE根据HL定理可得Rt△COM≌Rt△OEN,则ON=CM,由MN=OM+ON可求得MN的值,结合已知可求得FM的值,再根据线段的构成BF=OB+OF可求解.
5.【答案】 (1)证明:如图:连接
为等腰三角形
, 切⊙O于点
(2)解:结论成立;理由如下;
如图:连接EC,CD, 并延长 交⊙O于点H,连接
为⊙O的直径
切⊙O于点
(3)解:如图:连接OD,OG,
为 中点
与点F
在 中有
【解析】【分析】(1)先求出∠B=∠OCB,再求出∠PGC=∠PCG,最后求解即可;
(2)先求出∠H=∠PCD,再证明三角形相似,最后证明求解即可;
(3)先求出∠BGO=90°,再求出OB=5,最后利用锐角三角函数和勾股定理计算求解即可。
6.【答案】 (1)证明:如图,过点O作OF⊥AB于点F
∵AO平分∠CAB,
OC⊥AC,OF⊥AB,
∴OC=OF,
∴AB是⊙O的切线;
(2)解:如图,连接CE,
∵ED是⊙O的直径,
∴∠ECD=90°,
∴∠ECO+∠OCD=90°,
∵∠ACB=90°,
∴∠ACE+∠ECO=90°,
∴∠ACE=∠OCD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ACE=∠ODC,
∵∠CAE=∠CAE,
∴△ACE∽△ADC,
∴ ,
∵tan ,
∴ ;
(3)解:由(2)可知: ,
∴设AE=x,AC=2x,
∵△ACE∽△ADC,
∴ ,
∴AC2=AE AD,
∴(2x)2=x(x+6),
解得:x=2或x=0(不合题意,舍去),
∴AE=2,AC=4,
∴AO=AE+OE=2+3=5,
如图,连接CF交AD于点M
∵AC,AF是⊙O的切线,
∴AC=AF,∠CAO=∠OAF,
∴CF⊥AO,
∴∠ACO=∠CMO=90°,
∵∠COM=∠AOC,
∴△CMO∽△ACO,
∴ ,
∴OC2=OM OA,
∴OM= ,
∴CM= = ,
∴ .
【解析】【分析】(1)由题可过点O作OF⊥AB于点F,然后结合已知证OC=OF即可求解;
(2)连接CE,先证∠ACE=∠ODC,然后可证△ACE∽△ADC,于是可得比例式 , 由锐角三角函数tan∠D=即可求解;
(3)由(2)可设AE=x,AC=2x,由相似三角形的性质得AC2=AE AD,于是可求出AE,AC的长,则AO=AE+OE可求得AO的值;连接CF交AD于点M,证△CMO∽△ACO,可得OC2=OM OA,求出OM、CM的值,则CF=2CM可求解.
7.【答案】 (1)证明:∵四边形 为圆内接四边形
∴
∵
∴
∵
∴
(2)解:①如图1过点 作 于点
∵
∴
∴
设 ,则
∵
∴
∴
∵
∴
∴ ,
∴
∴
∴
②(i)当 时,如图,
∵
∴
∴
∴设
∴ ,
∴
∴ ,
∴
∴
(ii)当 时,
∵
∴
∴
∴
∴
∴
(iii)当 时,如图,连结
∵
∴
∴
∵
∴
∴
∴ ,∴
设 ,则
在 中, , ,
∴
综上所述,当线段 , , 中有两条相等时, 的值为 , 或
(3)
【解析】【解答】解:(3)设 ,
∴
∴
∵ 平分∠
∴∠
∴△
∴
∴
∴
∵△
∴
∴
∴在△ 中:
∴
∵
∴
如图,过 作 于
∵ 平分∠ ,
且△ 高相等,
∴
∴
∴
【分析】(1)由圆内接四边形的性质可得∠BFD+∠BED=180°,结合邻补角的性质可得∠AFD=∠BED,然后根据相似三角形的判定定理进行证明;
(2)①过点D作DM⊥BC于点M,由相似三角形的性质可得∠DBE=∠ADF,设DM=3x,则BM=9x,根据∠C的正切函数可得CM=4x,由勾股定理求出BC的值,然后根据CM+BM=AB=10可得x,进而得到CD、AD的值;
②当DE=DF时,由弦、弧、圆周角的关系可得∠ABD=∠CBD,求出tanC的值,设AD=DM=3x,则CM=4x,CD=5x,表示出AC,求出tan∠ABD的值,据此解答;当DE=BF时,同理可得∠DBE=∠FDB,推出DF∥BC,得到∠ADF=∠C,据此解答;当DF=BF时,连接EF,易得AC∥
EF,得到∠BEF=∠C,由等腰三角形的性质可得∠ABD=∠BDF=∠BEF=∠C,求出∠ABD的正切值,设AF=y,则DF=BF=6-y,在Rt△ADF中,由勾股定理可得y的值,据此解答;
(3)设AF=t,根据△AFD的面积可得AD,由角平分线的概念可得∠ABD=∠DBE=∠ADF,证明△ADF∽△ABD,△ADF∽△DBE,由相似三角形的性质可得AB、BF、BD,然后在Rt△ABD中,应用勾股定理可得t的值,进而得到BE,过D作DK⊥BC于K,由角平分线的性质可得AD=KD,证明△BEF∽△BCA,然后结合相似三角形的性质进行解答.
8.【答案】 (1)证明:∵EF⊥AB,
∴∠AFE=90°,
∴∠AEF+∠EAF=90°,
∵∠AEF=∠D,∠ABE=∠D,
∴∠ABE+∠EAF=90°,
∴∠AEB=90°,
∴AD⊥BC
(2)解:①证明:连接OA,AC.
∵AD⊥BC,
∴AE=ED,
∴CA=CD,
∴∠D=∠CAD,
∵∠GAE=2∠D,
∴∠CAG=∠CAD=∠D,
∵OC=OA,
∴∠OCA=∠OAC,
∵∠CEA=90°,
∴∠CAE+∠ACE=90°,
∴∠CAG+∠OAC=90°,
∴OA⊥AG,
∴AG是⊙O的切线.
②解:过点C作CH⊥AG于H.设CG=x,GH=y.
∵CA平分∠GAE,CH⊥AG,CE⊥AE,
∴CH=CE,
∵∠AEC=∠AHC=90°,AC=AC,EC=CH,
∴Rt△ACE≌Rt△ACH(HL),
∴AE=AH,
∵EF⊥AB,BC是直径,
∴∠BFE=∠BAC,
∴EF∥AC,
∴ ,
∵CE=4,
∴BE=10,
∵BC⊥AD,
∴ ,
∴∠CAE=∠ABC,
∵∠AEC=∠AEB=90°,
∴△AEB∽△CEA,
∴ ,
∴AE2=4×10,
∵AE>0,
∴AE= ,
∴AH=AE= ,
∵∠G=∠G,∠CHG=∠AEG=90°,
∴△GHC∽△GEA,
∴ ,
∴ ,
解得x= .
经检验:x= 是原方程的根且符合题意,
【解析】【分析】(1)由垂直的概念可得∠AFE=90°,由圆周角定理可得∠ABE=∠D,结合已知条件可推出∠AEB=90°,据此证明;
(2)①连接OA,AC,由垂径定理可得AE=ED,由等腰三角形的性质可得∠D=∠CAD,∠OCA=∠OAC,结合已知条件可得∠CAG=∠CAD=∠D,推出OA⊥AG,据此证明;
②过点C作CH⊥AG于H,设CG=x,GH=y,由角平分线的性质可得CH=CE,证明Rt△ACE≌Rt△ACH,推出EF∥AC,由平行线分线段成比例的性质可得BE,由弧、弦以及圆周角的关系可得∠CAE=∠ABC,证明△AEB∽△CEA,△GHC∽△GEA,然后由相似三角形的性质求解即可.
9.【答案】 (1)证明:连接OC,如图:
∵OP=CP,
∴∠OCP=∠COP,
∵OA=OC,
∴∠PAC=∠ACO,
设∠PAC=α,则∠ACO=α,
∴∠COP=∠PAC+∠ACO=2α=∠OCP,
∴∠ACP=∠OCP+∠ACO=3α,
∴∠ACP=3∠PAC
(2)证明:连接OC、OE、BC,如图:
∵CE⊥AD,
∴∠CFD=90°,
∴∠FCD=90°-∠ADC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠CAB=90°-∠ABC,
∵∠ADC=∠ABC,
∴∠FCD=∠CAB,
由(1)知:设∠CAB=α,则∠ACO=α,∠ACP=3α,
而∠FCD=∠CAB,
∴∠FCD=α,
∴∠OCE=∠ACP-∠FCD-∠ACO=α,
∴∠ACO=∠OCE,
∵OA=OC=OE,
∴∠OAC=∠ACO=∠OCE=∠E,
且OC=OC,
∴△AOC≌△EOC(AAS),
∴EC=AC
(3)解:连接OC、OE、BC,过O作OR⊥AC于R,过O作OS⊥CE于S,如图:
由(2)知:∠BAC=∠ACO=∠ECO=∠GCM=α,AC=EC,
∵∠ACB=∠CMG=90°,
∴△ACB∽△CMG,
∴ ,
设CG=x,⊙O的半径为r,则 ,
∴ ,
变形得: ①,
∵∠ACO=∠ECO,
∴CO是△ACG的角平分线,
∵OR⊥AC,OS⊥CE,
∴OR=OS,
∵ ,
∴ ,即 ,
∴ ,
∴ ,
∵弦CE、AB交于G,
∴AG BG=CG EG,即 ,
变形得: ②,
由①②得: ,
变形整理得x2-2x-24=0,
解得x=6或x=-4(舍去),
∴ ,
∴r=
【解析】【分析】(1)先求出 ∠PAC=∠ACO, 再求出 ∠COP=∠PAC+∠ACO=2α=∠OCP, 最后证明求解即可;
(2)先求出 ∠FCD=90°-∠ADC, 再求出 △AOC≌△EOC ,最后证明求解即可;
(3)先证明 △ACB∽△CMG, 再求出 , 最后求解即可。
10.【答案】 (1)证明:∵四边形 内接于 ,
∴ , ,
∵直径 ,
∴弧 弧 ,
∴ ,
∴ ,
∴ ∽ .
(2)解:①当 时,∵ ,
∴ ,
∴ 为直径,即 , , 三点共线,
∴弧 弧 ,
∵ 是 中点,∴弧 弧 弧 ,
∴弧 ,
由(1)得 ∽ ,
∴ ,
∴ ,
∵ ,
∴ ;
②当 时,则 ,
∴弧 弧 弧 ,
∴ ,
∵ 是 中点,∴ ,
∴ ≌ ,
∴ ,
∽ ,∴ ,
设 , ,则 ,解得 ,
即 ;
(3)解:如图,延长 至点 ,使 ,连接 ,
四边形 为圆内接四边形,
≌ ,
∴ ,
过点 作 ,连接 ,
∵点 是 的中点, ,
∴ , 是等边三角形,
∴ ,∴ ,
∵ ,
∴ , ,
由(1)得 ,
在 中, ;
【解析】【分析】(1)根据圆内接四边形的性质得到 , ,再根据直径 ,得到 ,即可得解;(2)分 和 两种情况进行讨论即可;(3)延长 至点 ,使 ,连接 ,易证 ≌ ,过点 作 ,连接 ,得到 是等边三角形,求出 , ,再根据 即可得解;
11.【答案】 (1)证明:如图1,连接 .
∵ 是半圆 的切线,
∴ .
又∵ ,
∴ .
∴ .
∵ ,
∴ .
∴ .
∵ , ,
∴ .
∵ ,
∴ .
(2)30 ;
【解析】【解答】解:(2) ①如图2,连接
∵四边形 为菱形,
∴
∵
∴ 为等边三角形
∴
∴ .
② 由(1)中得 ,
∴
∵ ,
∴ ,
∴
∴
即
∴
故答案为:30°,.
【分析】(1)连接OC,由切线的性质得OC⊥DE,推出OC∥AE,由平行线的性质可∠EAC=∠ACO,由等腰三角形的性质可得∠BAC=∠ACO,推出∠EAC=∠BAC,由垂直的概念可得∠AEC=∠AFC=90°,然后利用全等三角形的判定定理AAS进行证明;
(2)①连接OG,由菱形的性质可得OA=AG,推出△AOG为等边三角形,得到∠DAE=60°,据此求解;
② 由(1)中得∠EAC=∠BAC,推出BC=CG,由全等三角形的性质可得AE=AF,CE=CF,证明Rt△GCE≌Rt△BCF,得到GE=BF,推出AG+BF=AB-BF,据此求解.
12.【答案】 (1)证明:连接AC,BG,如图1所示
∵AB是 的直径,
(2)证明:如图2所示,
(3)解:连接AC、BC、BG,过点H作HM⊥AG于点M.
设AF=2k,BF=3k,则AB=5k.
∵AB是 的直径,
∴∠ACB=∠AGB=90°.
设
解得,
∴ 的半径
【解析】【分析】(1)连接AC,BG,由三角形的内角和知 , 因为 , 得到 , 由AB是 的直径,即可得到 ;
(2)由 , , 得出 , , ;
(3)连接AC、BC、BG,过点H作HM⊥AG于点M.设AF=2k,BF=3k,则AB=5k. , 得到
, 求得证出 , 设 由 , 解得证出因为得出 , 由此得出 的半径。
13.【答案】 (1)证明:∵ , 为 ,
∴
∵ ,
∴ ,
在 和 中,
∴ .
(2)解:结论: 与 相切.
理由:如下图,
连接 ,
∵ 是 的中垂线, ,
∴ ,
∴ .
由(1) ,而 ,
∴ ,
∴ ,
∴ ,
∵ 是 的半径,
∴ 与 相切.
(3)解:如下图,
连接 , ,
∵ 是 的平分线,
∴ . .
又∵ ,
∴ ,
∴ ,
∴ ,
∵ 是 的内接圆,
∴ 为 的直径,
∴ ,
又 ,
∴ ,
∴ ,
在 中, ,
∴
∴
在 中
∴
∴
即
【解析】【分析】(1)先求出 , 再利用ASA证明三角形全等即可;
(2)先求出 ,再求出 , 最后证明求解即可;
(3)先证明 , 再求出 ,最后利用勾股定理计算求解即可。
14.【答案】 (1)证明:如图,连接 ,
∵ 是 的切线,
∴ ,
∵ ,
∴ ,
∵ 为 的直径,
∴ ,
∴ ,
∴ ,
∴ ;
(2)解:如图,延长 交 于点 , 交 于点 ,
∵ 是 的直径, ,
∴ ,
∴ ,
∴ ,
在 中, ,
∴ ,
∴ , ,
∵ , ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ 的半径为20;
(3)解:在 中, ,
∴ ,
∴
∴
在 中,
∴
∴ .
【解析】【分析】(1) 连接 , 由切线的性质可得 , 即可得 , 由垂径定理可得结果;
(2) 延长 交 于点 , 交 于点 , 由垂径定理和弧、弦、圆心角定理可得 , 根据 可得 , 即可得GE的长度,由勾股定理可得BE的长度,即可得CE的长度,易证 , 即可得AE的长度,可得结果;
(3)由 可得AD的长度,即可得BD的长度,由垂径定理可得DM的长度,由勾股定理可得OM的长度,即可得四边形的面积.
15.【答案】 (1)证明:如图,连接 .
∵ 是直径,
∴ .
∴ .
∵ ,
∴ .
∴ 为 的垂直平分线.
∴ .
又 ,
∴ .
∴ .
∵ 是 的切线,
∴ .
∴ .
∴直线 与 相切
(2)证明:由(1)知 为 的切线,
∴ .
∴ 为 的切线,
∴ .
∵ ,
∴ .
∴ .
∴ .
∵ ,
∴ .
(3)解:如图,延长 交 于点H,连接 .
∵ ,
∴ .
易得 .
∴ .
即 .
设 ,则 .
解得 或0(舍去).
∴ .
∵ ,
.
∴ .
∴ .
又 ,
∴ .
∴
【解析】【分析】(1)连接OE,在利用垂直平分线的性质证出 , 再利用全等三角形的性质可得 , 即可证出直线 与 相切;
(2)先利用相似三角形的判定方法证出 , 再利用相似三角形的性质列出比例式化简即可;
(3)延长 交 于点H,连接 ,利用锐角三角函数求出 ,再证明 , 利用相似的性质列出比例式求解即可。
16.【答案】 (1)证明:连接 ,如图1所示:
为 的切线,
,
, 于 ,
, ,
在 和 中, ,
,
,
为 的切线;
(2)解:设 的半径为
由(1)可知
在 中,
则
,即 的半径为 .
(3)解:连接 ,如图2所示:
是直径,
由(1)知
,
,
,
, ,
是 的中位线,
,
,
设 ,则 , .
, ,
,
,
,
,即 ,
, .
,
设 , ,则 .
,
,
.
【解析】【分析】(1)连接OA,利用边边边定理证明△PBO≌△PAO,可得∠PBO=∠PAO =90°,即可得证;
(2)设 的半径为r,在Rt△OAE中根据勾股定理构建方程求解即可;
(3)连接AD,证明△ADE∽△POE,列出比例式得到OC是△ABD的中位线,然后由三角形中位线定理得出AD=2OC,根据已知条件设OC=2t,则BC=3t, AD=4t,再证明△PBC∽△BOC,推出EA和EP的比,设EA=8m,分别把EP和PA表示出来,再求出PB,最后根据三角函数定义求sin∠E的值.
17.【答案】 (1)证明: ,
为⊙ 的直径,
,
为 斜边上的中线,
,
,
,
.
(2)解:如图,将点 、 连接起来,
,
设 , ,
, ,
,
,
,
,
,
, ,
是 斜边上的中线,
, ,
又 ,
,
,
为⊙ 的直径, ,
,
,
,
在 和 中,
, ,
,
即 ,
,
.
(3)解:在 中, ,
设 , ,则 ,
由(2)得 ,
在 中, ,
,
,
,
,
,
,
,
,
即 .
【解析】【分析】(1)先由圆周角定理求出DF为直径,得出∠OCF=∠OFC,再由直角三角形斜边上中线的性质得出CM=MB,根据等边对等角得出∠MCB=∠B,从而得出∠B=∠OFC,最后根据同位角相等,两直线平行得出结论;
(2) 设MP=a,CP=4a,再证出△DOP∽△EMP,根据相似三角形的性质求出EP、则可得出DE的长, EM=a,根据直角三角形斜边上中线的性质求出AC=2DE=20 , 在Rt△ACE和Rt△MCE中利用勾股定理建立方程求出a,即可求解;
(3)设AE=m,CM=2r,由题意得出CE=xm,在Rt△MCE中运用勾股定理求出得到 , 再利用用△DOP∽△EMP,列比例式得出得出, , 代入即可得出函数关系式.
18.【答案】 (1)证明:连接AC,
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴DE=CE,
∴AD=AC,
∴∠ADC=∠ACD,
∵四边形ADCG是圆内接四边形,
∴∠CGF=∠ADC,
∵∠AGD=∠ACD,
∴∠CGF=∠AGD;
(2)解:如图,
①连接BD,
∵∠DGF=120°,
∴∠AGD=180°﹣120°=60°,
∴∠ACD=∠ABD=∠AGD=60°,
∴△ACD是等边三角形,
∵AB是直径,
∴∠ADB=90°,
∴sin∠ABD ,
∵AB=4,
∴CD=AD=2 ;
②∵∠DAG=∠FAD,∠AGD=∠ADC,
∴△ADG∽△AFD,
∴ ,
∵ ,AD=CD=2 ,
∴ ,DF=3 ,AF AG=AD2=12,
∴CF=DF﹣CD ,
∵∠GCF=∠DAF,∠F=∠F,
∴△FCG∽△FAD,
∴ ,
∴FG FA=FC FD 9,
∴ ,即 ,
∴ ,
∵ ,
∴ ,
∴ .
【解析】【分析】(1)连接AC,利用垂径定理可证得DE=EC,再利用等边对等角可证得∠ADC=∠ACD,利用圆内接四边形的性质,张凯德∠CGF=∠ADC,利用同弧所对的圆周角相等,可证得∠AGD=∠ACD,由此可证得结论;
(2)①连接BD,利用邻补角的定义求出∠AGD的度数,利用圆周角定理可证得∠ACD=∠ABD=∠AGD=60°,可推出△ACD是等边三角形,利用圆周角定理可证得∠ADB=90°,然后利用解直角三角形求出CD的长;②利用有两组对应角相等的两三角形相似,可证得△ADG∽△AFD,利用相似三角形的性质可求出DF,CF的长及AF AG的值;再证明△FCG∽△FAD,利用相似三角形的性质可得到FC FD 的值,然后求出FG与AG的比值,从而可求出△ADG与△AFD的面积之比.
19.【答案】 (1)解:连结 ,
∵直径 .
,
.
,
连结 ,则
在 中,
.
(2)解:①连结 ,
,
为直径,
.
②连结 ,过点A作 的垂线交 的延长线于点N,
为直径,
.
, .
.
(3)当 时, 和 的面积之比为 或
【解析】【解答】解:(3)当 时,F在O的右边时, ;当F在O的左边时, ;
当 时,则
,
解得 .
经检验: 是原方程的根且符合题意,
如图,连接
四边形 为 的内接四边形,
.
当 时, ,解得 .同理可得 .
∴当 时, 和 的面积之比为 或 .
【分析】(1)连接OD、BQ,先由勾股定理可求得OE的值,再由锐角三角形函数tan∠P=可求得tan∠P的值;在直角三角形ABQ中,由锐角三角形函数cos∠BAQ=可求得AQ的值;
(2)①连接BQ、AC,由圆周角定理可求解;
②连接BC,过点A作AC的垂线交CQ的延长线于点N,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得△FCB∽△FNA,由相似三角形的性质可得比例式可求解;
(3)由相似三角形的性质可求解.
20.【答案】 (1)证明: 与 相切于点 ,
,
半径 直径 ,
,
,
,
;
(2)解:①证明: ,
设 的半径为 ,
在 中,
在 中,
,
,
而 ,
四边形 是平行四边形:
作直径 连接 ,如图,
∵ ,半径为3
∴
∵四边形 是平行四边形,OD⊥CD,
∴ ,
为直径,
,
,
,
,
,
而
,
,即
.
【解析】【分析】(1)先利用切线的性质得到OD⊥CD,再证明AB∥CD,然后利用平行线的性质和圆周角定理得到结论;(2)①设⊙O的半径为r,利用正切的定义得到OG= r,则DG= r,则CD=3DG=2r,然后根据平行线的判定得到结论;②作直径DH,连接HE,如图,先计算出AG= ,CG=2 ,再证明△CDE∽△CAD,然后利用相似比计算DE的长.
21.【答案】 (1)证明:连接 .
是直径,
,
,
, ,
,
,
,
为 的切线
(2)证明: , ,
,
,
,
,
,
,
,
,
(3)解::如图,过点 作 于 .
是直径,
,
,
可以假设 , ,
,
,
, ,
,
,
,
,
,
,
,
,
,
, ,
,
,
,
,
, , ,
, ,
【解析】【分析】(1)欲证明 是 的切线,只要证明 即可.(2)证明 ,可得结论.(3)过点 作 于 .由题意 ,可以假设 , ,证明 ,可得 ,推出 , ,再证明 ,推出 ,推出 , ,由 ,推出 ,可得 ,利用勾股定理求出 , ,可得结论
1.如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1).判断直线CD与⊙O的位置关系,并说明理由;
(2).若tan∠ADC= ,AC=2,求⊙O的半径;
(3).如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.
2.如图,已知 , 是 的直径, , 与 的边 , 分别交于点 , ,连接 并延长,与 的延长线交于点 , .
(1).求证: 是 的切线;
(2).若 ,求 的值;
(3).在(2)的条件下,若 的平分线 交 于点 ,连接 交 于点 ,求 的值.
3.如图所示, 是 的直径,点 、 是 上不同的两点,直线 交线段 于点 ,交过点 的直线 于点 ,若 ,且 .
(1)求证:直线 是 的切线;
(2)连接 、 、 、 ,若 .
①求证: ;
②过点 作 ,交线段 于点 ,点 为线段 的中点,若 ,求线段 的长度.
4.如图, 为 的直径,C为 上一点,连接 ,D为 延长线上一点,连接 ,且 .
(1)求证: 是 的切线;
(2)若 的半径为 , 的面积为 ,求 的长;
(3)在(2)的条件下,E为 上一点,连接 交线段 于点F,若 ,求 的长.
5.如图,已知 是 的直径. 是 的弦,弦 垂直 于点F,交 于点G.过点C作 的切线交 的延长线于点P
(1)求证: ;
(2)判断 是否成立?若成立,请证明该结论;
(3)若G为 中点, , ,求 的长.
6.如图1,在直角△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作圆O
(1).求证:AB是⊙O的切线;
(2).已知AO交圆O于点E,延长AO交圆O于点D,tan∠D= ,求 的值;
(3).如图2,在(2)条件下,若AB与⊙O的切点为点F,连接CF交AD于点G,设⊙O的半径为3,求CF的长.
7.如图,在 中, , 是边 上一动点,且不与 , 两点重合,连结 ,过点 作 交边 于点 , 的外接圆交边 于另一点 ,连结 .
(1).求证: .
(2).当 , 时.
①若 ,求 的长.
②当线段 , , 中有两条相等时,求出所有符合条件的 的值.
(3).若 平分 , , ,则 .
8.如图,BC是⊙O的直径,AD是⊙O的弦,AD交BC于点E,连接AB,CD,过点E作EF⊥AB,垂足为F,∠AEF=∠D.
(1).求证:AD⊥BC;
(2).点G在BC的延长线上,连接AG,∠DAG=2∠D.
①求证:AG与⊙O相切;
②当 ,CE=4时,直接写出CG的长.
9.如图, 为 的直径, 为 延长线上一点,点 在 上,连接 交 于点 , .
(1)求证: ;
(2)过点 作弦 ,垂足为 , 交 于点 ,求证: ;
(3)在(2)的条件下,过点 作 ,垂足为 ,若 , ,求 的半径.
10.如图1, 是 的直径,弦 于点 , 是 上一点, , 的延长线交于点 .
(1)求证: ∽ .
(2)若 是 的中点,当 与 的一边平行时,求 的值.
(3)如图2,点 是 的中点, ,连结 , , .当 时,求 的值.
11.如图. 为半圆 的直径,点 为半圆 上一点,过点 作半圆 的切线 交 的延长线于点 .过点 作 于点 ,交半圆 于点 ,过点 作 于点 ,连接 , , .
(1).求证: ;
(2).填空:①连接 ,当 的度数为 时,四边形 为菱形;
②若 . ,则 的长为 .
12.如图, 为 直径,弦 交 于点E,G为 上一点,连接 交 于点F,交 于点H,连接 ,且 .
(1)如图1,求证: ;
(2)如图2,若 ,求证: ;
(3)如图3,在(2)的条件下,若 ,求 的半径.
13.如图,在 中, , 的垂直平分线分别与 , 及 的延长线相交于点D , E , F , 且 . 是 的外接圆, 的平分线交 于点G , 交 于点H , 连接 、 .
(1)求证: ;
(2)试判断 与 的位置关系,并说明理由;
(3)若 ,求 的值.
14.如图,四边形 内接于 , 为 的直径, 是 的切线, 交 的延长线于点 ,过点 作 于点 ,连接 交 于点 .
(1)求证: ;
(2)若 , ,求 的半径;
(3)在(2)的条件下,求四边形 的面积.
15.如图, 与 的边 相切于点C , 与 分别交于点D , E , 是 的直径,过点A作 交 于M , N两点(点M在线段 上).
(1)求证:直线 与 相切;
(2)求证: ;
(3)若 ,求 的长.
16.如图, 为 的切线, 为切点,过 作 的垂线 ,垂足为点 ,交 于点 .连接 并延长交 于点 ,交 的延长线于点 .
(1)求证: 为 的切线;
(2)若 , ,求 的半径;
(3)若 ,求 的值.
17.如图,在 中, , , 是 的中点,以 为直径的⊙ 与 的三边分别交于点 、 、 ,连接 、 , 与 交于点 ﹒
(1)求证: ;
(2)若 , ,求⊙ 的直径 的长;
(3)设 , ,求 与 之间的函数关系式﹒
18.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是 上一点,AG,DC的延长线交于点F,连接AD,GD,GC.
(1)求证:∠CGF=∠AGD.
(2)已知∠DGF=120°,AB=4.
①求CD的长.
②若 ,求△ADG与△AFD的面积之比.
19.(提出问题)
如图1,直径 垂直弦 于点E, , ,点P是 延长线上异于点D的一个动点,连结 交 于点Q,连结 交 于点F,则点F的位置随着点P位置的改变而改变.
(1)(特殊位置探究)
当 时,求 和线段 的长;
(2)(一般规律探究)
如图2,连结 , .在点P运动过程中,设 , .
①求证: ;
②求y与x之间的函数关系式:
(3)(解决问题)
当 时,求 和 的面积之比.(直接写出答案)
20.如图,在 中,半径 直径 与 相切于点 连接 交 于点 交 于点 ,连接 并延长交 于点 ,连接 .
(1)求证: ;
(2)若
①求证:四边形 是平行四边形;
②连接 ,当 的半径为 时,求 的长.
21.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,D为圆上一点,且B,D两点位于AC异侧,连接BD,交AC于E,点F为BD延长线上一点,连接AF,使得∠DAF=∠ABD.
(1)求证:AF为⊙O的切线;
(2)当点D为EF的中点时,求证:AD2=AO AE;
(3)在(2)的条件下,若sin∠BAC= ,AF=2 ,求BF的长.
答案解析部分
1.【答案】 (1)解:CD与⊙O相切,理由:
如图1,连接OD,
∵OB=OD,
∴∠ODB=∠CBD,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB为⊙O的直径,
∴∠ADB=∠ADO+∠ODB=90°,
∴∠CDA+∠ADO=90°,
∴∠CDO=90°,
∴OD⊥CD,
∴CD与⊙O相切
(2)解:由(1)知,∠CBD=∠ADC,
∵tan∠ADC= ,
∴tan∠CBD= ,
在Rt△ADB中,tan∠CBD= = ,
∵∠C=∠C,∠ADC=∠CBD,
∴△CAD∽△CDB,
∴ ,
∴CD=2CA=4,
∴CB=2CD=8,
∴AB=CB CA=8 2=6,
∴OA=OB= AB=3
(3)解:如图2,连接OE,过点E作EG⊥BD于G,
∵DE平分∠ADB,
∴∠ADE=∠BDE=45°,
∴∠BOE=2∠BDE=90°,
∴BE= =3 ,
在Rt△ABD中,AD2+BD2=AB2=62 ,
∵ = ,
∴AD= ,BD= ,
∵EG⊥BD,∠BDE=45°,
∴∠DEG=∠BDE=45°,
∴DG=EG,
设DG=EG=x,则BG=BD DG= x,
在Rt△BEG中,EG2+BG2=BE2=(3 )2=18,
∴x2+( x)2=18,
∴x= 或x= (舍),
∴EG= ,
∴sin∠DBE=
【解析】【分析】(1)连接OD,由等腰三角形的性质结合已知条件可得∠CDA=∠ODB,由圆周角定理可得∠ADB=90°,推出∠CDO=90°,据此判断;
(2)由(1)知,∠CBD=∠ADC,则tan∠ADC=tan∠CBD= , 证明△CAD∽△CDB,由相似三角形的性质可得CD、CB的值,进而求出AB、OA的值;
(3)连接OE,过点E作EG⊥BD于G,由角平分线的概念可得∠ADE=∠BDE=45°,则∠BOE=90°,由勾股定理求出BE、AD、BD的值,设DG=EG=x,则BG= x,然后在Rt△BEG中,应用勾股定理求出x的值,进而得到sin∠DBE的值.
2.【答案】 (1)证明:如图,连接DF,
∵ 是 的直径,
∴ .
∴DF∥AE.
∵四边形ABCD是平行四边形,
∴AE∥OC.
∴DF∥OC.
∴ .
∵ ,
∴ .
∵ ,
∴ .
∵ ,
∴ .
∴ .
∴ .
∴ 是 的切线
(2)解:∵ ,
∴ .
∴ .
∴ .
∴ .
∵ ,
∴ .
设 ,则 .
由勾股定理得 ,
即 ,
解得 , (不合题意,舍去).
∴ .
∵ ,
∴
(3)解:连接MN,并延长CO与AF, 分别相交于点P,点Q,连接AQ,
∵四边形ABCD是平行四边形,
∴ , ,AB∥OC.
∴ ,
∵ 平分 ,
∴ .
∴ .
∴ .
∵
∴ .
∵ ,
∴ .
∴ .
∴ .
∴ .
∵AB∥OC,
∴ .
∴ .
∵ ,
∴ .
在Rt△APO中,由勾股定理得 .
∴ .
在Rt△APH中,由勾股定理得 .
∵ ,
∴ .
∵ ,
∴ .
∴ .
∴
【解析】【分析】(1)连接DF,利用平行线的判定定理可证得DF∥AE,利用平行四边形的性质可证得AE∥OC,由此可证得DF∥OC;再利用平行线的性质及等腰三角形的性质可推出∠FAD=∠OCD,根据∠FDA+∠FAD=90°,可得到∠ODC=90°;然后利用切线的判定定理可证得结论.
(2)利用余角的性质可证得∠FDG=∠FAD,由此可推出△FDG∽△FAD,利用相似三角形的性质,可证得FD2=FG·FA,设DF=x,可表示出AF的长,利用勾股定理建立关于x的方程,解方程求出x的值,可求出DF的长;再利用锐角三角函数的定义及∠AEF=∠ADF,可求出cos∠AEF的值.
(3)连接MN,并延长CO与AF, 分别相交于点P,点Q,连接AQ,利用平行四边形的性质和平行线的性质可证得OC=AB,AO=BC,∠CHB=∠ABH,再利用角平分线的定义去证明∠CHB=∠BCH,由此可求出CH的长;然后解直角三角形求出OC,AB的长,由此可求出MH的长及HQ的长,可推出HQ=AB;然后求出AP的长,利用勾股定理在Rt△APO中求出OP的长,可得到PH的长;在Rt△APH中,利用勾股定理求出AH的长;利用有两组对应角相等的两三角形相似,可证得△MHN∽△AHQ,利用相似三角形的性质可求出AB与NH的比值.
3.【答案】 (1)证明:因为 ,且 ,
∴ ,
∴ ,
∴ ,
∴直线 是 的切线
(2)解:①∵ ,
又∵ ,
∴ ,
∵ ,
∴. ;
②∵ ,
∴ ,
设圆的半径为r,
∵ , ,
∴ ,
∴ ;
∵点 为线段 的中点,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴线段 的长度为1
【解析】【分析】(1)由题意用勾股定理的逆定理易证∠ECF=90°,然后根据圆的切线的判定可求解;
(2)①证明∠DAC=∠EOB,∠DCA=∠EBO,根据有两个角对应相等的两个三角形相似可求解;
②由①中知:△ACD∽△OBE,再由相似三角形的性质可得比例式 , 结合已知可求得AC的值,再由平行线分线段成比例定理"两条直线被一组平行线所截,截得的对应线段的长度成比例"可得比例式 , 于是可求出CG的值,再根据线段的构成MG=CM-CG可求解.
4.【答案】 (1)证明:连接 ,
∵AB为⊙O直径,
∴∠ACB=90°,
∴∠CAB+∠CBO=90°,
又∵OB=OC,
∴∠CBO=∠BCO,
∴∠CAB+∠BCO=90°
∵∠BCD=∠A,
∴∠BCD+∠BCO=90°,
∴OC⊥CD
∴CD为⊙O切线
(2)解:过点C作 于点M,
∵ 的半径为 ,
∴AB= ,
∵ 的面积为 ,
∴CM=2,
在Rt△CMO中,CO= ,CM=2,
∴OM=1,
由(1)得∠OCD=∠CMO=90°,
∵∠COM=∠COD,
∴△COM∽△DOC,
∴ ,
∴ ,
∴
(3)解:过点E作 于点N,连接 ,
∵ , ,
∴△FCM∽△FEN,
∴ ,
由(2)得CM=2,OM=1,
∴EN=OM=1,
∵OC=OE,
∴Rt△COM≌Rt△OEN,
∴ON=CM=2,
∴MN=3,
∵ ,
∴FM=2,
∵OM=1,
∴OF=1,
∵BF=OB+OF,
∴
【解析】∴MN=3,
∵ ,
∴FM=2,
∵OM=1,
∴OF=1,
∵BF=OB+OF,
∴
【分析】(1)连接OC,由直径所对的圆周角是直角可得∠ACB=∠A+∠ABC=90°,由等边对等角得∠ABC=∠BCO,结合已知可得∠ACB=90°,然后根据圆的切线的判定可求解;
(2)过C作CM⊥AB于M,由△ABC的面积为2=AB×CM可求得CM的值,根据有两个角对应相等的两个三角形全等可得△COM∽△DOC,可得比例式 , 则CD的值可求解;
(3) 过点E作于点N,连接OE,由CM⊥AB,EN⊥AB,可得△FCM∽△FEN,于是可得比例式 , 由(2)得CM=2,OM=1,于是可得EN=OM,结合已知OC=OE根据HL定理可得Rt△COM≌Rt△OEN,则ON=CM,由MN=OM+ON可求得MN的值,结合已知可求得FM的值,再根据线段的构成BF=OB+OF可求解.
5.【答案】 (1)证明:如图:连接
为等腰三角形
, 切⊙O于点
(2)解:结论成立;理由如下;
如图:连接EC,CD, 并延长 交⊙O于点H,连接
为⊙O的直径
切⊙O于点
(3)解:如图:连接OD,OG,
为 中点
与点F
在 中有
【解析】【分析】(1)先求出∠B=∠OCB,再求出∠PGC=∠PCG,最后求解即可;
(2)先求出∠H=∠PCD,再证明三角形相似,最后证明求解即可;
(3)先求出∠BGO=90°,再求出OB=5,最后利用锐角三角函数和勾股定理计算求解即可。
6.【答案】 (1)证明:如图,过点O作OF⊥AB于点F
∵AO平分∠CAB,
OC⊥AC,OF⊥AB,
∴OC=OF,
∴AB是⊙O的切线;
(2)解:如图,连接CE,
∵ED是⊙O的直径,
∴∠ECD=90°,
∴∠ECO+∠OCD=90°,
∵∠ACB=90°,
∴∠ACE+∠ECO=90°,
∴∠ACE=∠OCD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ACE=∠ODC,
∵∠CAE=∠CAE,
∴△ACE∽△ADC,
∴ ,
∵tan ,
∴ ;
(3)解:由(2)可知: ,
∴设AE=x,AC=2x,
∵△ACE∽△ADC,
∴ ,
∴AC2=AE AD,
∴(2x)2=x(x+6),
解得:x=2或x=0(不合题意,舍去),
∴AE=2,AC=4,
∴AO=AE+OE=2+3=5,
如图,连接CF交AD于点M
∵AC,AF是⊙O的切线,
∴AC=AF,∠CAO=∠OAF,
∴CF⊥AO,
∴∠ACO=∠CMO=90°,
∵∠COM=∠AOC,
∴△CMO∽△ACO,
∴ ,
∴OC2=OM OA,
∴OM= ,
∴CM= = ,
∴ .
【解析】【分析】(1)由题可过点O作OF⊥AB于点F,然后结合已知证OC=OF即可求解;
(2)连接CE,先证∠ACE=∠ODC,然后可证△ACE∽△ADC,于是可得比例式 , 由锐角三角函数tan∠D=即可求解;
(3)由(2)可设AE=x,AC=2x,由相似三角形的性质得AC2=AE AD,于是可求出AE,AC的长,则AO=AE+OE可求得AO的值;连接CF交AD于点M,证△CMO∽△ACO,可得OC2=OM OA,求出OM、CM的值,则CF=2CM可求解.
7.【答案】 (1)证明:∵四边形 为圆内接四边形
∴
∵
∴
∵
∴
(2)解:①如图1过点 作 于点
∵
∴
∴
设 ,则
∵
∴
∴
∵
∴
∴ ,
∴
∴
∴
②(i)当 时,如图,
∵
∴
∴
∴设
∴ ,
∴
∴ ,
∴
∴
(ii)当 时,
∵
∴
∴
∴
∴
∴
(iii)当 时,如图,连结
∵
∴
∴
∵
∴
∴
∴ ,∴
设 ,则
在 中, , ,
∴
综上所述,当线段 , , 中有两条相等时, 的值为 , 或
(3)
【解析】【解答】解:(3)设 ,
∴
∴
∵ 平分∠
∴∠
∴△
∴
∴
∴
∵△
∴
∴
∴在△ 中:
∴
∵
∴
如图,过 作 于
∵ 平分∠ ,
且△ 高相等,
∴
∴
∴
【分析】(1)由圆内接四边形的性质可得∠BFD+∠BED=180°,结合邻补角的性质可得∠AFD=∠BED,然后根据相似三角形的判定定理进行证明;
(2)①过点D作DM⊥BC于点M,由相似三角形的性质可得∠DBE=∠ADF,设DM=3x,则BM=9x,根据∠C的正切函数可得CM=4x,由勾股定理求出BC的值,然后根据CM+BM=AB=10可得x,进而得到CD、AD的值;
②当DE=DF时,由弦、弧、圆周角的关系可得∠ABD=∠CBD,求出tanC的值,设AD=DM=3x,则CM=4x,CD=5x,表示出AC,求出tan∠ABD的值,据此解答;当DE=BF时,同理可得∠DBE=∠FDB,推出DF∥BC,得到∠ADF=∠C,据此解答;当DF=BF时,连接EF,易得AC∥
EF,得到∠BEF=∠C,由等腰三角形的性质可得∠ABD=∠BDF=∠BEF=∠C,求出∠ABD的正切值,设AF=y,则DF=BF=6-y,在Rt△ADF中,由勾股定理可得y的值,据此解答;
(3)设AF=t,根据△AFD的面积可得AD,由角平分线的概念可得∠ABD=∠DBE=∠ADF,证明△ADF∽△ABD,△ADF∽△DBE,由相似三角形的性质可得AB、BF、BD,然后在Rt△ABD中,应用勾股定理可得t的值,进而得到BE,过D作DK⊥BC于K,由角平分线的性质可得AD=KD,证明△BEF∽△BCA,然后结合相似三角形的性质进行解答.
8.【答案】 (1)证明:∵EF⊥AB,
∴∠AFE=90°,
∴∠AEF+∠EAF=90°,
∵∠AEF=∠D,∠ABE=∠D,
∴∠ABE+∠EAF=90°,
∴∠AEB=90°,
∴AD⊥BC
(2)解:①证明:连接OA,AC.
∵AD⊥BC,
∴AE=ED,
∴CA=CD,
∴∠D=∠CAD,
∵∠GAE=2∠D,
∴∠CAG=∠CAD=∠D,
∵OC=OA,
∴∠OCA=∠OAC,
∵∠CEA=90°,
∴∠CAE+∠ACE=90°,
∴∠CAG+∠OAC=90°,
∴OA⊥AG,
∴AG是⊙O的切线.
②解:过点C作CH⊥AG于H.设CG=x,GH=y.
∵CA平分∠GAE,CH⊥AG,CE⊥AE,
∴CH=CE,
∵∠AEC=∠AHC=90°,AC=AC,EC=CH,
∴Rt△ACE≌Rt△ACH(HL),
∴AE=AH,
∵EF⊥AB,BC是直径,
∴∠BFE=∠BAC,
∴EF∥AC,
∴ ,
∵CE=4,
∴BE=10,
∵BC⊥AD,
∴ ,
∴∠CAE=∠ABC,
∵∠AEC=∠AEB=90°,
∴△AEB∽△CEA,
∴ ,
∴AE2=4×10,
∵AE>0,
∴AE= ,
∴AH=AE= ,
∵∠G=∠G,∠CHG=∠AEG=90°,
∴△GHC∽△GEA,
∴ ,
∴ ,
解得x= .
经检验:x= 是原方程的根且符合题意,
【解析】【分析】(1)由垂直的概念可得∠AFE=90°,由圆周角定理可得∠ABE=∠D,结合已知条件可推出∠AEB=90°,据此证明;
(2)①连接OA,AC,由垂径定理可得AE=ED,由等腰三角形的性质可得∠D=∠CAD,∠OCA=∠OAC,结合已知条件可得∠CAG=∠CAD=∠D,推出OA⊥AG,据此证明;
②过点C作CH⊥AG于H,设CG=x,GH=y,由角平分线的性质可得CH=CE,证明Rt△ACE≌Rt△ACH,推出EF∥AC,由平行线分线段成比例的性质可得BE,由弧、弦以及圆周角的关系可得∠CAE=∠ABC,证明△AEB∽△CEA,△GHC∽△GEA,然后由相似三角形的性质求解即可.
9.【答案】 (1)证明:连接OC,如图:
∵OP=CP,
∴∠OCP=∠COP,
∵OA=OC,
∴∠PAC=∠ACO,
设∠PAC=α,则∠ACO=α,
∴∠COP=∠PAC+∠ACO=2α=∠OCP,
∴∠ACP=∠OCP+∠ACO=3α,
∴∠ACP=3∠PAC
(2)证明:连接OC、OE、BC,如图:
∵CE⊥AD,
∴∠CFD=90°,
∴∠FCD=90°-∠ADC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠CAB=90°-∠ABC,
∵∠ADC=∠ABC,
∴∠FCD=∠CAB,
由(1)知:设∠CAB=α,则∠ACO=α,∠ACP=3α,
而∠FCD=∠CAB,
∴∠FCD=α,
∴∠OCE=∠ACP-∠FCD-∠ACO=α,
∴∠ACO=∠OCE,
∵OA=OC=OE,
∴∠OAC=∠ACO=∠OCE=∠E,
且OC=OC,
∴△AOC≌△EOC(AAS),
∴EC=AC
(3)解:连接OC、OE、BC,过O作OR⊥AC于R,过O作OS⊥CE于S,如图:
由(2)知:∠BAC=∠ACO=∠ECO=∠GCM=α,AC=EC,
∵∠ACB=∠CMG=90°,
∴△ACB∽△CMG,
∴ ,
设CG=x,⊙O的半径为r,则 ,
∴ ,
变形得: ①,
∵∠ACO=∠ECO,
∴CO是△ACG的角平分线,
∵OR⊥AC,OS⊥CE,
∴OR=OS,
∵ ,
∴ ,即 ,
∴ ,
∴ ,
∵弦CE、AB交于G,
∴AG BG=CG EG,即 ,
变形得: ②,
由①②得: ,
变形整理得x2-2x-24=0,
解得x=6或x=-4(舍去),
∴ ,
∴r=
【解析】【分析】(1)先求出 ∠PAC=∠ACO, 再求出 ∠COP=∠PAC+∠ACO=2α=∠OCP, 最后证明求解即可;
(2)先求出 ∠FCD=90°-∠ADC, 再求出 △AOC≌△EOC ,最后证明求解即可;
(3)先证明 △ACB∽△CMG, 再求出 , 最后求解即可。
10.【答案】 (1)证明:∵四边形 内接于 ,
∴ , ,
∵直径 ,
∴弧 弧 ,
∴ ,
∴ ,
∴ ∽ .
(2)解:①当 时,∵ ,
∴ ,
∴ 为直径,即 , , 三点共线,
∴弧 弧 ,
∵ 是 中点,∴弧 弧 弧 ,
∴弧 ,
由(1)得 ∽ ,
∴ ,
∴ ,
∵ ,
∴ ;
②当 时,则 ,
∴弧 弧 弧 ,
∴ ,
∵ 是 中点,∴ ,
∴ ≌ ,
∴ ,
∽ ,∴ ,
设 , ,则 ,解得 ,
即 ;
(3)解:如图,延长 至点 ,使 ,连接 ,
四边形 为圆内接四边形,
≌ ,
∴ ,
过点 作 ,连接 ,
∵点 是 的中点, ,
∴ , 是等边三角形,
∴ ,∴ ,
∵ ,
∴ , ,
由(1)得 ,
在 中, ;
【解析】【分析】(1)根据圆内接四边形的性质得到 , ,再根据直径 ,得到 ,即可得解;(2)分 和 两种情况进行讨论即可;(3)延长 至点 ,使 ,连接 ,易证 ≌ ,过点 作 ,连接 ,得到 是等边三角形,求出 , ,再根据 即可得解;
11.【答案】 (1)证明:如图1,连接 .
∵ 是半圆 的切线,
∴ .
又∵ ,
∴ .
∴ .
∵ ,
∴ .
∴ .
∵ , ,
∴ .
∵ ,
∴ .
(2)30 ;
【解析】【解答】解:(2) ①如图2,连接
∵四边形 为菱形,
∴
∵
∴ 为等边三角形
∴
∴ .
② 由(1)中得 ,
∴
∵ ,
∴ ,
∴
∴
即
∴
故答案为:30°,.
【分析】(1)连接OC,由切线的性质得OC⊥DE,推出OC∥AE,由平行线的性质可∠EAC=∠ACO,由等腰三角形的性质可得∠BAC=∠ACO,推出∠EAC=∠BAC,由垂直的概念可得∠AEC=∠AFC=90°,然后利用全等三角形的判定定理AAS进行证明;
(2)①连接OG,由菱形的性质可得OA=AG,推出△AOG为等边三角形,得到∠DAE=60°,据此求解;
② 由(1)中得∠EAC=∠BAC,推出BC=CG,由全等三角形的性质可得AE=AF,CE=CF,证明Rt△GCE≌Rt△BCF,得到GE=BF,推出AG+BF=AB-BF,据此求解.
12.【答案】 (1)证明:连接AC,BG,如图1所示
∵AB是 的直径,
(2)证明:如图2所示,
(3)解:连接AC、BC、BG,过点H作HM⊥AG于点M.
设AF=2k,BF=3k,则AB=5k.
∵AB是 的直径,
∴∠ACB=∠AGB=90°.
设
解得,
∴ 的半径
【解析】【分析】(1)连接AC,BG,由三角形的内角和知 , 因为 , 得到 , 由AB是 的直径,即可得到 ;
(2)由 , , 得出 , , ;
(3)连接AC、BC、BG,过点H作HM⊥AG于点M.设AF=2k,BF=3k,则AB=5k. , 得到
, 求得证出 , 设 由 , 解得证出因为得出 , 由此得出 的半径。
13.【答案】 (1)证明:∵ , 为 ,
∴
∵ ,
∴ ,
在 和 中,
∴ .
(2)解:结论: 与 相切.
理由:如下图,
连接 ,
∵ 是 的中垂线, ,
∴ ,
∴ .
由(1) ,而 ,
∴ ,
∴ ,
∴ ,
∵ 是 的半径,
∴ 与 相切.
(3)解:如下图,
连接 , ,
∵ 是 的平分线,
∴ . .
又∵ ,
∴ ,
∴ ,
∴ ,
∵ 是 的内接圆,
∴ 为 的直径,
∴ ,
又 ,
∴ ,
∴ ,
在 中, ,
∴
∴
在 中
∴
∴
即
【解析】【分析】(1)先求出 , 再利用ASA证明三角形全等即可;
(2)先求出 ,再求出 , 最后证明求解即可;
(3)先证明 , 再求出 ,最后利用勾股定理计算求解即可。
14.【答案】 (1)证明:如图,连接 ,
∵ 是 的切线,
∴ ,
∵ ,
∴ ,
∵ 为 的直径,
∴ ,
∴ ,
∴ ,
∴ ;
(2)解:如图,延长 交 于点 , 交 于点 ,
∵ 是 的直径, ,
∴ ,
∴ ,
∴ ,
在 中, ,
∴ ,
∴ , ,
∵ , ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ 的半径为20;
(3)解:在 中, ,
∴ ,
∴
∴
在 中,
∴
∴ .
【解析】【分析】(1) 连接 , 由切线的性质可得 , 即可得 , 由垂径定理可得结果;
(2) 延长 交 于点 , 交 于点 , 由垂径定理和弧、弦、圆心角定理可得 , 根据 可得 , 即可得GE的长度,由勾股定理可得BE的长度,即可得CE的长度,易证 , 即可得AE的长度,可得结果;
(3)由 可得AD的长度,即可得BD的长度,由垂径定理可得DM的长度,由勾股定理可得OM的长度,即可得四边形的面积.
15.【答案】 (1)证明:如图,连接 .
∵ 是直径,
∴ .
∴ .
∵ ,
∴ .
∴ 为 的垂直平分线.
∴ .
又 ,
∴ .
∴ .
∵ 是 的切线,
∴ .
∴ .
∴直线 与 相切
(2)证明:由(1)知 为 的切线,
∴ .
∴ 为 的切线,
∴ .
∵ ,
∴ .
∴ .
∴ .
∵ ,
∴ .
(3)解:如图,延长 交 于点H,连接 .
∵ ,
∴ .
易得 .
∴ .
即 .
设 ,则 .
解得 或0(舍去).
∴ .
∵ ,
.
∴ .
∴ .
又 ,
∴ .
∴
【解析】【分析】(1)连接OE,在利用垂直平分线的性质证出 , 再利用全等三角形的性质可得 , 即可证出直线 与 相切;
(2)先利用相似三角形的判定方法证出 , 再利用相似三角形的性质列出比例式化简即可;
(3)延长 交 于点H,连接 ,利用锐角三角函数求出 ,再证明 , 利用相似的性质列出比例式求解即可。
16.【答案】 (1)证明:连接 ,如图1所示:
为 的切线,
,
, 于 ,
, ,
在 和 中, ,
,
,
为 的切线;
(2)解:设 的半径为
由(1)可知
在 中,
则
,即 的半径为 .
(3)解:连接 ,如图2所示:
是直径,
由(1)知
,
,
,
, ,
是 的中位线,
,
,
设 ,则 , .
, ,
,
,
,
,即 ,
, .
,
设 , ,则 .
,
,
.
【解析】【分析】(1)连接OA,利用边边边定理证明△PBO≌△PAO,可得∠PBO=∠PAO =90°,即可得证;
(2)设 的半径为r,在Rt△OAE中根据勾股定理构建方程求解即可;
(3)连接AD,证明△ADE∽△POE,列出比例式得到OC是△ABD的中位线,然后由三角形中位线定理得出AD=2OC,根据已知条件设OC=2t,则BC=3t, AD=4t,再证明△PBC∽△BOC,推出EA和EP的比,设EA=8m,分别把EP和PA表示出来,再求出PB,最后根据三角函数定义求sin∠E的值.
17.【答案】 (1)证明: ,
为⊙ 的直径,
,
为 斜边上的中线,
,
,
,
.
(2)解:如图,将点 、 连接起来,
,
设 , ,
, ,
,
,
,
,
,
, ,
是 斜边上的中线,
, ,
又 ,
,
,
为⊙ 的直径, ,
,
,
,
在 和 中,
, ,
,
即 ,
,
.
(3)解:在 中, ,
设 , ,则 ,
由(2)得 ,
在 中, ,
,
,
,
,
,
,
,
,
即 .
【解析】【分析】(1)先由圆周角定理求出DF为直径,得出∠OCF=∠OFC,再由直角三角形斜边上中线的性质得出CM=MB,根据等边对等角得出∠MCB=∠B,从而得出∠B=∠OFC,最后根据同位角相等,两直线平行得出结论;
(2) 设MP=a,CP=4a,再证出△DOP∽△EMP,根据相似三角形的性质求出EP、则可得出DE的长, EM=a,根据直角三角形斜边上中线的性质求出AC=2DE=20 , 在Rt△ACE和Rt△MCE中利用勾股定理建立方程求出a,即可求解;
(3)设AE=m,CM=2r,由题意得出CE=xm,在Rt△MCE中运用勾股定理求出得到 , 再利用用△DOP∽△EMP,列比例式得出得出, , 代入即可得出函数关系式.
18.【答案】 (1)证明:连接AC,
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴DE=CE,
∴AD=AC,
∴∠ADC=∠ACD,
∵四边形ADCG是圆内接四边形,
∴∠CGF=∠ADC,
∵∠AGD=∠ACD,
∴∠CGF=∠AGD;
(2)解:如图,
①连接BD,
∵∠DGF=120°,
∴∠AGD=180°﹣120°=60°,
∴∠ACD=∠ABD=∠AGD=60°,
∴△ACD是等边三角形,
∵AB是直径,
∴∠ADB=90°,
∴sin∠ABD ,
∵AB=4,
∴CD=AD=2 ;
②∵∠DAG=∠FAD,∠AGD=∠ADC,
∴△ADG∽△AFD,
∴ ,
∵ ,AD=CD=2 ,
∴ ,DF=3 ,AF AG=AD2=12,
∴CF=DF﹣CD ,
∵∠GCF=∠DAF,∠F=∠F,
∴△FCG∽△FAD,
∴ ,
∴FG FA=FC FD 9,
∴ ,即 ,
∴ ,
∵ ,
∴ ,
∴ .
【解析】【分析】(1)连接AC,利用垂径定理可证得DE=EC,再利用等边对等角可证得∠ADC=∠ACD,利用圆内接四边形的性质,张凯德∠CGF=∠ADC,利用同弧所对的圆周角相等,可证得∠AGD=∠ACD,由此可证得结论;
(2)①连接BD,利用邻补角的定义求出∠AGD的度数,利用圆周角定理可证得∠ACD=∠ABD=∠AGD=60°,可推出△ACD是等边三角形,利用圆周角定理可证得∠ADB=90°,然后利用解直角三角形求出CD的长;②利用有两组对应角相等的两三角形相似,可证得△ADG∽△AFD,利用相似三角形的性质可求出DF,CF的长及AF AG的值;再证明△FCG∽△FAD,利用相似三角形的性质可得到FC FD 的值,然后求出FG与AG的比值,从而可求出△ADG与△AFD的面积之比.
19.【答案】 (1)解:连结 ,
∵直径 .
,
.
,
连结 ,则
在 中,
.
(2)解:①连结 ,
,
为直径,
.
②连结 ,过点A作 的垂线交 的延长线于点N,
为直径,
.
, .
.
(3)当 时, 和 的面积之比为 或
【解析】【解答】解:(3)当 时,F在O的右边时, ;当F在O的左边时, ;
当 时,则
,
解得 .
经检验: 是原方程的根且符合题意,
如图,连接
四边形 为 的内接四边形,
.
当 时, ,解得 .同理可得 .
∴当 时, 和 的面积之比为 或 .
【分析】(1)连接OD、BQ,先由勾股定理可求得OE的值,再由锐角三角形函数tan∠P=可求得tan∠P的值;在直角三角形ABQ中,由锐角三角形函数cos∠BAQ=可求得AQ的值;
(2)①连接BQ、AC,由圆周角定理可求解;
②连接BC,过点A作AC的垂线交CQ的延长线于点N,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得△FCB∽△FNA,由相似三角形的性质可得比例式可求解;
(3)由相似三角形的性质可求解.
20.【答案】 (1)证明: 与 相切于点 ,
,
半径 直径 ,
,
,
,
;
(2)解:①证明: ,
设 的半径为 ,
在 中,
在 中,
,
,
而 ,
四边形 是平行四边形:
作直径 连接 ,如图,
∵ ,半径为3
∴
∵四边形 是平行四边形,OD⊥CD,
∴ ,
为直径,
,
,
,
,
,
而
,
,即
.
【解析】【分析】(1)先利用切线的性质得到OD⊥CD,再证明AB∥CD,然后利用平行线的性质和圆周角定理得到结论;(2)①设⊙O的半径为r,利用正切的定义得到OG= r,则DG= r,则CD=3DG=2r,然后根据平行线的判定得到结论;②作直径DH,连接HE,如图,先计算出AG= ,CG=2 ,再证明△CDE∽△CAD,然后利用相似比计算DE的长.
21.【答案】 (1)证明:连接 .
是直径,
,
,
, ,
,
,
,
为 的切线
(2)证明: , ,
,
,
,
,
,
,
,
,
(3)解::如图,过点 作 于 .
是直径,
,
,
可以假设 , ,
,
,
, ,
,
,
,
,
,
,
,
,
,
, ,
,
,
,
,
, , ,
, ,
【解析】【分析】(1)欲证明 是 的切线,只要证明 即可.(2)证明 ,可得结论.(3)过点 作 于 .由题意 ,可以假设 , ,证明 ,可得 ,推出 , ,再证明 ,推出 ,推出 , ,由 ,推出 ,可得 ,利用勾股定理求出 , ,可得结论
