2021-2022学年华东师大版八年级数学上册第11章数的开方期中复习训练 (word版含解析)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册第11章数的开方期中复习训练 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 237.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 14:47:11 | ||
图片预览




文档简介
2021-2022学年华师大版八年级数学上册《第11章数的开方》期中复习训练(附答案)
1.下列说法错误的是( )
A.1的平方根是±1 B.﹣1的立方根是﹣1
C.是2的一个平方根 D.﹣3是的一个平方根
2.一个正数的平方根是2m+3和m+1,则这个数为( )
A.﹣ B. C. D.1或
3.,,则1720的平方根为( )
A.13.11 B.±13.11 C.41.47 D.±41.47
4.已知实数a,b,c在数轴上对应点的位置如图所示,|a+b|+|a+c|﹣|b﹣c|的值是( )
A.0 B.2a+2b C.2b﹣2c D.2a+2c
5.下列各数3.14,,0.0,,2.131 331 333 1…(相邻两个1之间3的个数逐次多1),,,其中无理数的个数为( )
A.2个 B.3个 C.4个 D.5个
6.在如图所示的数轴上表示﹣2的点在( )
A.点A和点B之间 B.点B和点C之间
C.点C和点D之间 D.点D和点E之间
7.若a=,b=﹣|﹣|,c=,则a、b、c的大小关系是( )
A.a>b>c B.c>a>b C.b>a>c D.c>b>a
8.当式子的值取最小值时,a的取值为( )
A.0 B. C.﹣1 D.1
9.下列各选项的结果表示的数中不是无理数的是( )
A.如图,直径为单位1的圆从数轴上的原点沿着数轴无滑动地顺时针滚动一周到达点A,点A表示的数 B.5的算术平方根 C.9的立方根 D.
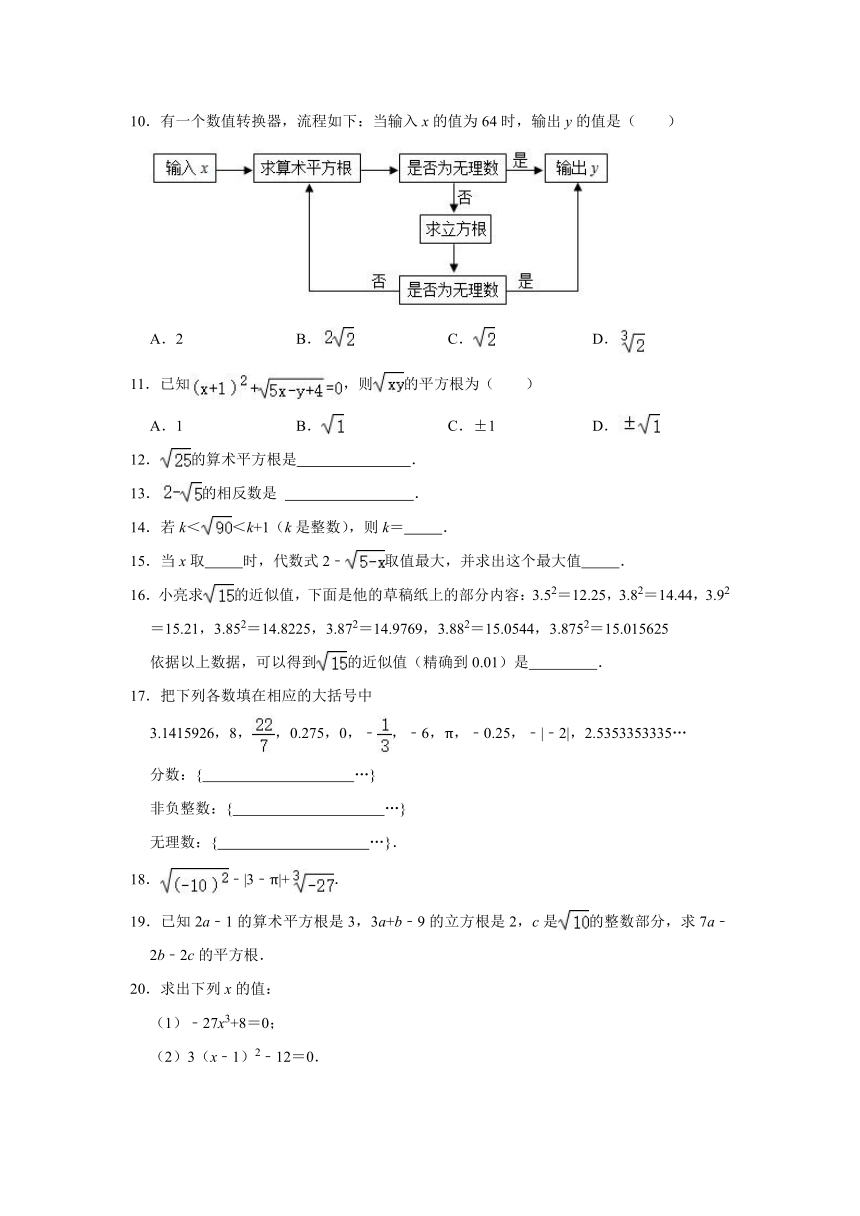
10.有一个数值转换器,流程如下:当输入x的值为64时,输出y的值是( )
A.2 B. C. D.
11.已知,则的平方根为( )
A.1 B. C.±1 D.
12.的算术平方根是 .
13.的相反数是 .
14.若k<<k+1(k是整数),则k= .
15.当x取 时,代数式2﹣取值最大,并求出这个最大值 .
16.小亮求的近似值,下面是他的草稿纸上的部分内容:3.52=12.25,3.82=14.44,3.92=15.21,3.852=14.8225,3.872=14.9769,3.882=15.0544,3.8752=15.015625
依据以上数据,可以得到的近似值(精确到0.01)是 .
17.把下列各数填在相应的大括号中
3.1415926,8,,0.275,0,﹣,﹣6,π,﹣0.25,﹣|﹣2|,2.5353353335…
分数:{ …}
非负整数:{ …}
无理数:{ …}.
18.﹣|3﹣π|+.
19.已知2a﹣1的算术平方根是3,3a+b﹣9的立方根是2,c是的整数部分,求7a﹣2b﹣2c的平方根.
20.求出下列x的值:
(1)﹣27x3+8=0;
(2)3(x﹣1)2﹣12=0.
21.(1)若x,y为实数,且x=+4,求(x﹣y)2的平方根;
(2)已知x﹣2的平方根是±2,2x+y+7的立方根是3,求x2+y2的算术平方根.
22.按要求填空:
(1)填表:
a 0.0004 0.04 4 400
(2)根据你发现规律填空:
已知:=2.638,则= ,= ;
已知:=0.06164,=61.64,则x= .
23.把下列各数填入相应的括号里
﹣2,100π,﹣5,0.8,﹣|+5.2|,0,0.1010010001…,﹣(﹣4)
正有理数集合:{}
整数集合:{}
负分数集合:{}
无理数集合:{}.
24.阅读理解
∵<<,即2<<3.
∴1<﹣1<2
∴﹣1的整数部分为1.
∴﹣1的小数部分为﹣2.
解决问题:
已知a是﹣3的整数部分,b是﹣3的小数部分,求(﹣a)3+(b+4)2的平方根.
25.小丽想在一块面积为36m2正方形纸片上,沿着边的方向裁出一块面积为30m2的长方形纸片,并且使它的长宽的比为2:1.问:小丽能否用这块正方形纸片裁出符合要求的长方形纸片,为什么?
26.阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用﹣1来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<()2<32,即2<<3,∴的整数部分为2,小数部分为(﹣2).
请解答:
(1)的整数部分是 ,小数部分是
(2)如果的小数部分为a,的整数部分为b,求a+b﹣的值.
27.阅读下面的文字,解答问题
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用﹣1来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:<<,即2<<3,
∴的整数部分为2,小数部分为(﹣2)
请解答:
(1)的整数部分是 ,小数部分是 .
(2)如果的小数部分为a,的整数部分为b,求|a﹣b|+的值.
(3)已知:9+=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
参考答案
1.解:A.1的平方根是±1,正确;
B.﹣1的立方根是﹣1,正确;
C.是2的一个平方根,正确;
D.,3的平方根是±,故错误;
故选:D.
2.解:(2m+3)+(m+1)=0,
m=﹣,
m+1=﹣,
(m+1)=,
故选:C.
3.解:,则1720的平方根为,
故选:D.
4.解:由数轴可得:a+c<0,b﹣c>0,a+b>0,
则|a+b|+|a+c|﹣|b﹣c|,
=a+b﹣a﹣c﹣b+c,
=0;
故选:A.
5.解:在所列的7个数中,无理数是,2.131 331 333 1…(相邻两个1之间3的个数逐次多1),共3个.
故选:B.
6.解:∵,
∴,
∴,
即﹣2的值在2和3之间,数轴上表示﹣2的点在点C和点D之间.
故选:C.
7.解:a=﹣=﹣3,b=﹣|﹣|=﹣,c=﹣=﹣(﹣2)=2,
∴c>b>a,
故选:D.
8.解:∵2a+1≥0,
∴当式子的值取最小值时,2a+1=0,
∴a的取值为﹣.
故选:B.
9.解:A、由题意可知原点到点A的长是圆的周长,而圆的周长=πd=π×1=π,所以点A表示的数是π.是无理数,这个选项错误;
B、5的算术平方根是无理数,这个选项错误;
C、9的立方根是无理数,这个选项错误;
D、=12,12是有理数,这个选项正确;
故选:D.
10.解:当输入x的值为64时,
=8,是有理数,
=2,是有理数,
是无理数,输出,即y=,
故选:C.
11.解:根据题意得,x+1=0,5x﹣y+4=0,
解得x=﹣1,y=﹣1,
所以,==1,
所以,的平方根为±1.
故选:C.
12.解:∵52=25,
∴=5,
∴的算术平方根是.
故答案为:.
13.解:2﹣的相反数是﹣2.
故答案为:﹣2.
14.解:∵81<90<100,
∴9<<10,
则k=9,
故答案为:9.
15.解:当5﹣x=0,即x=5时,
代数式2﹣取值最大,
此时这个最大值2.
故答案为:5,2.
16.解:∵3.52=12.25,3.82=14.44,3.92=15.21,3.852=14.8225,3.872=14.9769,3.882=15.0544,3.8752=15.015625,
∴≈3.87,
故答案为:3.87.
17.解:分数:{3.1415926,,0.275,﹣,﹣0.25};
非负整数:{8,0};
无理数:{π,2.5353353335…},
故答案为:3.1415926,,0.275,﹣,﹣0.25;8,0,;π,2.5353353335…,
18.解:原式=10﹣(π﹣3)﹣3
=10﹣π+3﹣3
=10﹣π.
19.解:∵2a﹣1的算术平方根是3,
∴2a﹣1=9,
∴a=5,
∵3a+b﹣9的立方根是2,
∴3a+b﹣9=8,
∴b=2,
∵c是的整数部分,,
∴c=3,
∴7a﹣2b﹣2c=35﹣4﹣6=25,
∴7a﹣2b﹣2c的平方根是±5.
20.解:(1)∵﹣27x3+8=0,
∴﹣27x3=﹣8,
则x3=,
解得:x=;
(2)∵3(x﹣1)2﹣12=0,
∴3(x﹣1)2=12,
∴(x﹣1)2=4,
则x﹣1=±2
解得:x=3或x=﹣1.
21.解:(1)由题意得:,
解得y=3,
∴x=4,
∴(x﹣y)2=1,
∴(x﹣y)2的平方根是±1.
(2)由x﹣2的平方根是±2,2x+y+7的立方根是3,得
x﹣2=4,2x+y+7=27,
解得x=6,y=8.
∴x2+y2=100,
∴x2+y2的算术平方根是10.
22.解:(1)=0.02,=0.2,=2,=20;
(2)==2.638×10=26.38,
==2.638×10﹣2=0.02638;
∵=0.06164,=61.64,61.64=0.06164×10﹣3
∴x=3800.
故答案为:0.02、0.2、2、20;26.38、0.02638;3800.
23.解:正有理数集合:{0.8,﹣(﹣4)…};
整数集合:{﹣2,0,…};
负分数集合:{﹣5,﹣|+5.2|…};
无理数集合:{100π,0.1010010001…}.
24.解:∵<<,
∴4<<5,
∴1<﹣3<2,
∴a=1,b=﹣4,
∴(﹣a)3+(b+4)2
=(﹣1)3+(﹣4+4)2
=﹣1+17
=16,
∴(﹣a)3+(b+4)2的平方根是:±4.
25.解:不能.设长方形纸片的长为2xcm,宽为xcm,则:
2x x=30,
2x2=30,
x2=15,
x=,
则长方形纸片的长为2cm,
因为2>6,而正形纸片的边长为cm=6cm,所以不能裁剪出符合要求的长方形.
26.解:(1)∵<<,
∴3<<4,
∴的整数部分是3,小数部分是:﹣3;
故答案为:3,﹣3;
(2)∵<<,
∴的小数部分为:a=﹣2,
∵<<,
∴的整数部分为b=6,
∴a+b﹣=﹣2+6﹣=4.
27.解:(1)∵,
∴的整数部分是7,小数部分是﹣7.
故答案为:7;﹣7.
(2)∵,
∴,
∵,
∴b=2,
∴|a﹣b|+
=
=
=5.
(3)∵,
∴11<9+<12,
∵9+=x+y,其中x是整数,且0<y<1,
∴x=11,y==,
∴x﹣y==,
∴x﹣y的相反数是:.
1.下列说法错误的是( )
A.1的平方根是±1 B.﹣1的立方根是﹣1
C.是2的一个平方根 D.﹣3是的一个平方根
2.一个正数的平方根是2m+3和m+1,则这个数为( )
A.﹣ B. C. D.1或
3.,,则1720的平方根为( )
A.13.11 B.±13.11 C.41.47 D.±41.47
4.已知实数a,b,c在数轴上对应点的位置如图所示,|a+b|+|a+c|﹣|b﹣c|的值是( )
A.0 B.2a+2b C.2b﹣2c D.2a+2c
5.下列各数3.14,,0.0,,2.131 331 333 1…(相邻两个1之间3的个数逐次多1),,,其中无理数的个数为( )
A.2个 B.3个 C.4个 D.5个
6.在如图所示的数轴上表示﹣2的点在( )
A.点A和点B之间 B.点B和点C之间
C.点C和点D之间 D.点D和点E之间
7.若a=,b=﹣|﹣|,c=,则a、b、c的大小关系是( )
A.a>b>c B.c>a>b C.b>a>c D.c>b>a
8.当式子的值取最小值时,a的取值为( )
A.0 B. C.﹣1 D.1
9.下列各选项的结果表示的数中不是无理数的是( )
A.如图,直径为单位1的圆从数轴上的原点沿着数轴无滑动地顺时针滚动一周到达点A,点A表示的数 B.5的算术平方根 C.9的立方根 D.
10.有一个数值转换器,流程如下:当输入x的值为64时,输出y的值是( )
A.2 B. C. D.
11.已知,则的平方根为( )
A.1 B. C.±1 D.
12.的算术平方根是 .
13.的相反数是 .
14.若k<<k+1(k是整数),则k= .
15.当x取 时,代数式2﹣取值最大,并求出这个最大值 .
16.小亮求的近似值,下面是他的草稿纸上的部分内容:3.52=12.25,3.82=14.44,3.92=15.21,3.852=14.8225,3.872=14.9769,3.882=15.0544,3.8752=15.015625
依据以上数据,可以得到的近似值(精确到0.01)是 .
17.把下列各数填在相应的大括号中
3.1415926,8,,0.275,0,﹣,﹣6,π,﹣0.25,﹣|﹣2|,2.5353353335…
分数:{ …}
非负整数:{ …}
无理数:{ …}.
18.﹣|3﹣π|+.
19.已知2a﹣1的算术平方根是3,3a+b﹣9的立方根是2,c是的整数部分,求7a﹣2b﹣2c的平方根.
20.求出下列x的值:
(1)﹣27x3+8=0;
(2)3(x﹣1)2﹣12=0.
21.(1)若x,y为实数,且x=+4,求(x﹣y)2的平方根;
(2)已知x﹣2的平方根是±2,2x+y+7的立方根是3,求x2+y2的算术平方根.
22.按要求填空:
(1)填表:
a 0.0004 0.04 4 400
(2)根据你发现规律填空:
已知:=2.638,则= ,= ;
已知:=0.06164,=61.64,则x= .
23.把下列各数填入相应的括号里
﹣2,100π,﹣5,0.8,﹣|+5.2|,0,0.1010010001…,﹣(﹣4)
正有理数集合:{}
整数集合:{}
负分数集合:{}
无理数集合:{}.
24.阅读理解
∵<<,即2<<3.
∴1<﹣1<2
∴﹣1的整数部分为1.
∴﹣1的小数部分为﹣2.
解决问题:
已知a是﹣3的整数部分,b是﹣3的小数部分,求(﹣a)3+(b+4)2的平方根.
25.小丽想在一块面积为36m2正方形纸片上,沿着边的方向裁出一块面积为30m2的长方形纸片,并且使它的长宽的比为2:1.问:小丽能否用这块正方形纸片裁出符合要求的长方形纸片,为什么?
26.阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用﹣1来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<()2<32,即2<<3,∴的整数部分为2,小数部分为(﹣2).
请解答:
(1)的整数部分是 ,小数部分是
(2)如果的小数部分为a,的整数部分为b,求a+b﹣的值.
27.阅读下面的文字,解答问题
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用﹣1来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:<<,即2<<3,
∴的整数部分为2,小数部分为(﹣2)
请解答:
(1)的整数部分是 ,小数部分是 .
(2)如果的小数部分为a,的整数部分为b,求|a﹣b|+的值.
(3)已知:9+=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
参考答案
1.解:A.1的平方根是±1,正确;
B.﹣1的立方根是﹣1,正确;
C.是2的一个平方根,正确;
D.,3的平方根是±,故错误;
故选:D.
2.解:(2m+3)+(m+1)=0,
m=﹣,
m+1=﹣,
(m+1)=,
故选:C.
3.解:,则1720的平方根为,
故选:D.
4.解:由数轴可得:a+c<0,b﹣c>0,a+b>0,
则|a+b|+|a+c|﹣|b﹣c|,
=a+b﹣a﹣c﹣b+c,
=0;
故选:A.
5.解:在所列的7个数中,无理数是,2.131 331 333 1…(相邻两个1之间3的个数逐次多1),共3个.
故选:B.
6.解:∵,
∴,
∴,
即﹣2的值在2和3之间,数轴上表示﹣2的点在点C和点D之间.
故选:C.
7.解:a=﹣=﹣3,b=﹣|﹣|=﹣,c=﹣=﹣(﹣2)=2,
∴c>b>a,
故选:D.
8.解:∵2a+1≥0,
∴当式子的值取最小值时,2a+1=0,
∴a的取值为﹣.
故选:B.
9.解:A、由题意可知原点到点A的长是圆的周长,而圆的周长=πd=π×1=π,所以点A表示的数是π.是无理数,这个选项错误;
B、5的算术平方根是无理数,这个选项错误;
C、9的立方根是无理数,这个选项错误;
D、=12,12是有理数,这个选项正确;
故选:D.
10.解:当输入x的值为64时,
=8,是有理数,
=2,是有理数,
是无理数,输出,即y=,
故选:C.
11.解:根据题意得,x+1=0,5x﹣y+4=0,
解得x=﹣1,y=﹣1,
所以,==1,
所以,的平方根为±1.
故选:C.
12.解:∵52=25,
∴=5,
∴的算术平方根是.
故答案为:.
13.解:2﹣的相反数是﹣2.
故答案为:﹣2.
14.解:∵81<90<100,
∴9<<10,
则k=9,
故答案为:9.
15.解:当5﹣x=0,即x=5时,
代数式2﹣取值最大,
此时这个最大值2.
故答案为:5,2.
16.解:∵3.52=12.25,3.82=14.44,3.92=15.21,3.852=14.8225,3.872=14.9769,3.882=15.0544,3.8752=15.015625,
∴≈3.87,
故答案为:3.87.
17.解:分数:{3.1415926,,0.275,﹣,﹣0.25};
非负整数:{8,0};
无理数:{π,2.5353353335…},
故答案为:3.1415926,,0.275,﹣,﹣0.25;8,0,;π,2.5353353335…,
18.解:原式=10﹣(π﹣3)﹣3
=10﹣π+3﹣3
=10﹣π.
19.解:∵2a﹣1的算术平方根是3,
∴2a﹣1=9,
∴a=5,
∵3a+b﹣9的立方根是2,
∴3a+b﹣9=8,
∴b=2,
∵c是的整数部分,,
∴c=3,
∴7a﹣2b﹣2c=35﹣4﹣6=25,
∴7a﹣2b﹣2c的平方根是±5.
20.解:(1)∵﹣27x3+8=0,
∴﹣27x3=﹣8,
则x3=,
解得:x=;
(2)∵3(x﹣1)2﹣12=0,
∴3(x﹣1)2=12,
∴(x﹣1)2=4,
则x﹣1=±2
解得:x=3或x=﹣1.
21.解:(1)由题意得:,
解得y=3,
∴x=4,
∴(x﹣y)2=1,
∴(x﹣y)2的平方根是±1.
(2)由x﹣2的平方根是±2,2x+y+7的立方根是3,得
x﹣2=4,2x+y+7=27,
解得x=6,y=8.
∴x2+y2=100,
∴x2+y2的算术平方根是10.
22.解:(1)=0.02,=0.2,=2,=20;
(2)==2.638×10=26.38,
==2.638×10﹣2=0.02638;
∵=0.06164,=61.64,61.64=0.06164×10﹣3
∴x=3800.
故答案为:0.02、0.2、2、20;26.38、0.02638;3800.
23.解:正有理数集合:{0.8,﹣(﹣4)…};
整数集合:{﹣2,0,…};
负分数集合:{﹣5,﹣|+5.2|…};
无理数集合:{100π,0.1010010001…}.
24.解:∵<<,
∴4<<5,
∴1<﹣3<2,
∴a=1,b=﹣4,
∴(﹣a)3+(b+4)2
=(﹣1)3+(﹣4+4)2
=﹣1+17
=16,
∴(﹣a)3+(b+4)2的平方根是:±4.
25.解:不能.设长方形纸片的长为2xcm,宽为xcm,则:
2x x=30,
2x2=30,
x2=15,
x=,
则长方形纸片的长为2cm,
因为2>6,而正形纸片的边长为cm=6cm,所以不能裁剪出符合要求的长方形.
26.解:(1)∵<<,
∴3<<4,
∴的整数部分是3,小数部分是:﹣3;
故答案为:3,﹣3;
(2)∵<<,
∴的小数部分为:a=﹣2,
∵<<,
∴的整数部分为b=6,
∴a+b﹣=﹣2+6﹣=4.
27.解:(1)∵,
∴的整数部分是7,小数部分是﹣7.
故答案为:7;﹣7.
(2)∵,
∴,
∵,
∴b=2,
∴|a﹣b|+
=
=
=5.
(3)∵,
∴11<9+<12,
∵9+=x+y,其中x是整数,且0<y<1,
∴x=11,y==,
∴x﹣y==,
∴x﹣y的相反数是:.
