9.3代数式的值-同步练习-2021-2022学年沪教版(上海)七年级数学第一学期(word版含答案)
文档属性
| 名称 | 9.3代数式的值-同步练习-2021-2022学年沪教版(上海)七年级数学第一学期(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 323.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 14:19:43 | ||
图片预览


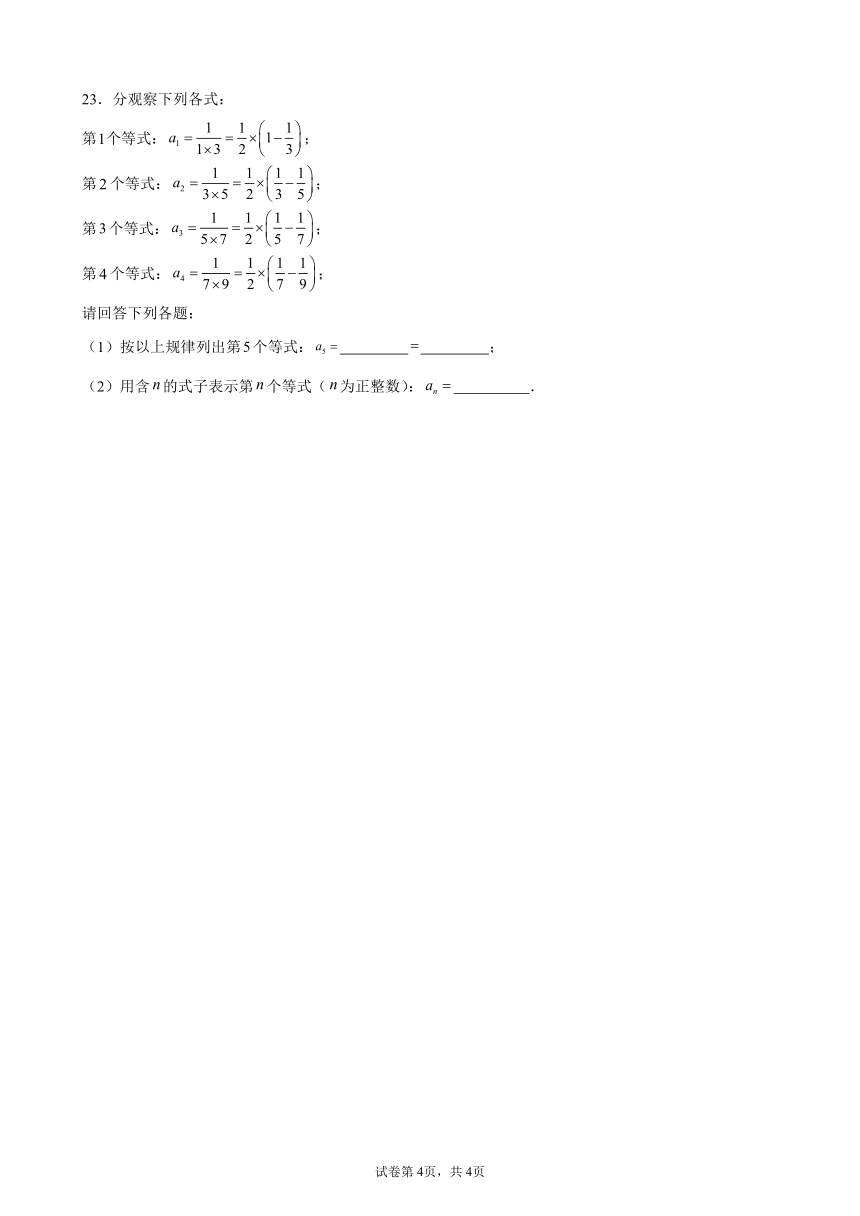

文档简介
2021-2022学年七年级数学第一学期(沪教版)教材同步
9.3代数式的值-同步练习
时间:60分钟
一、单选题
1.若|a+9|+(b﹣8)2=0,则(a+b)2021的值为( )
A.﹣1 B.0 C.1 D.2
2.规定,则的值为( )
A. B. C. D.
3.已知a=|﹣3|,则a﹣4=( )
A.﹣7 B.1 C.﹣1 D.﹣1或﹣7
4.当x=2与x=-2时,代数式x4-2x2+3的两个值( )
A.相等 B.互为倒数 C.互为相反数 D.既不相等也不互为相反数
5.|a+2|+(b+1)2=0,那么a-b的值是( )
A.1 B.﹣1 C.-3 D.3
6.若,则的值为( )
A.-42 B.42 C.-2 D.22
7.按照如图所示的方法排列黑色小正方形地砖,则第13个图案中黑色小正方形地砖的块数是( )
A.253 B.273 C.293 D.313
8.如图图形都是由同样大小的“○”按- -定的规律组成,其中第1个图形中一共有5个“○”,第2个图形中一共有12个“○”,第3个图形中一共有21个“○”,……,则第7个图形中“○”的个数是( )
A.60 B.66 C.77 D.96
二、填空题
9.当代数式x2+3x+5的值为7时,代数式3x2+9x﹣2的值是 ___.
10.若a、b互为相反数,则a+(b﹣2)的值为______________.
11.如果,互为相反数,,互为倒数,那么2020xy=_______.
12.若,则_____
13.若与互为相反数,则= _____.
14.观察一列数:,,,,,…,根据规律,第n个数是_______(用含n的代数式表示).
15.当||=+2时,19+3+27的值是______.
16.一组按规律排列的式子:,其中第7个式子是_______,第n个式子是_______(n为正整数).
三、解答题
17.已知a与b互为相反数,c与d互为倒数,m的绝对值为2,求式子﹣cd+m3的值.
18.已知,.
(1)若,求的值.
(2)若,求的值.
19.已知,试求:
(1)的值;
(2)的值.
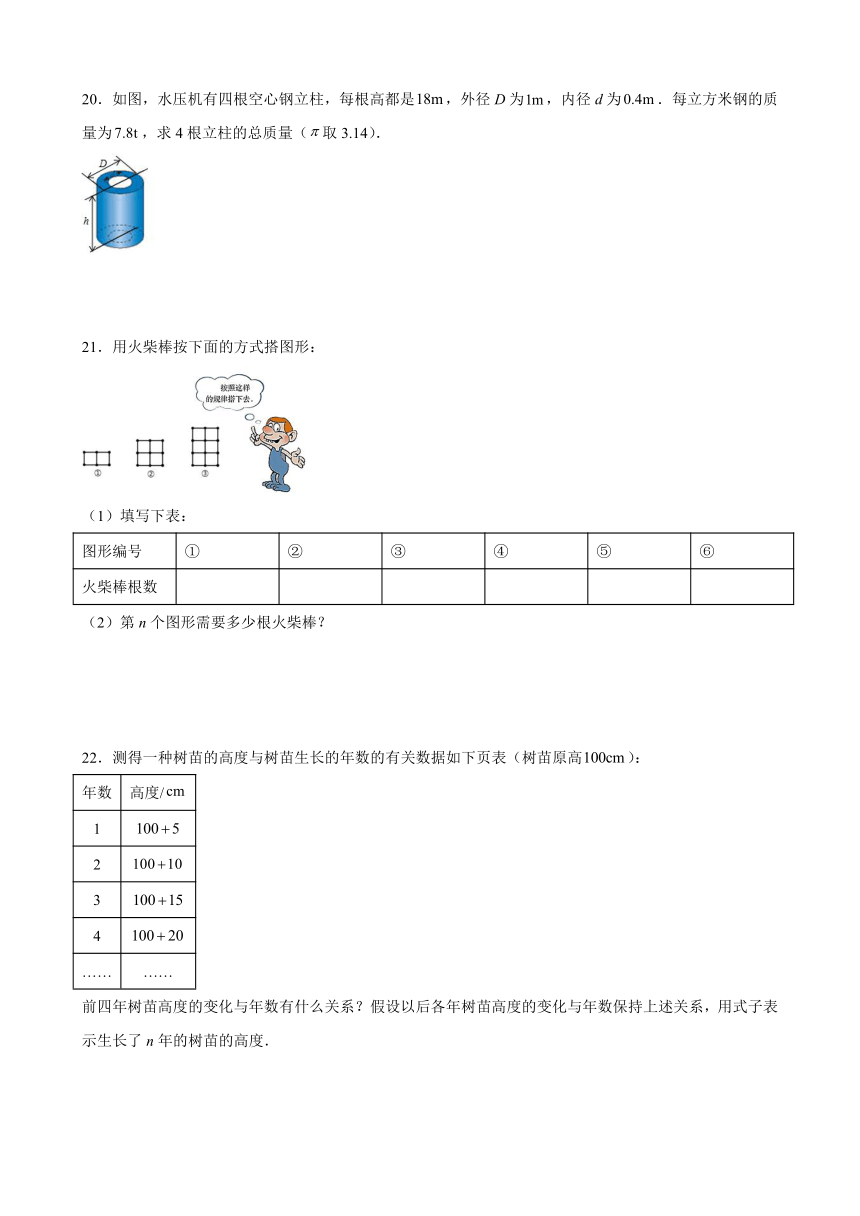
20.如图,水压机有四根空心钢立柱,每根高都是,外径D为,内径d为.每立方米钢的质量为,求4根立柱的总质量(取3.14).
21.用火柴棒按下面的方式搭图形:
(1)填写下表:
图形编号 ① ② ③ ④ ⑤ ⑥
火柴棒根数
(2)第n个图形需要多少根火柴棒?
22.测得一种树苗的高度与树苗生长的年数的有关数据如下页表(树苗原高):
年数 高度/
1
2
3
4
…… ……
前四年树苗高度的变化与年数有什么关系?假设以后各年树苗高度的变化与年数保持上述关系,用式子表示生长了n年的树苗的高度.
23.分观察下列各式:
第个等式:;
第个等式:;
第个等式:;
第个等式:;
请回答下列各题:
(1)按以上规律列出第个等式: ;
(2)用含的式子表示第个等式(为正整数): .
试卷第1页,共3页
参考答案
1.A
【解析】解:由题意得,a+9=0,b-8=0,
解得a=-9,b=8,
所以,(a+b)2021=(-9+8)2021=(-1)2021=-1.
故答案为:A.
2.C
【解析】解:
已知:,
将,代入即为:
,
故选:C.
3.C
【解析】解:∵a=|﹣3|=3,
∴a﹣4=3-4=-1,
故选C.
4.A
【解析】解:当x=2时,
∴x4-2x2+3=24-2×22+3,
=16-8+3,
=11.
当x=-2时,
∴x4-2x2+3=(-2)4-2×(-2)2+3,
=16-8+3,
=11.
∴相等.
故答案为:A.
5.B
【解析】解:∵|a+2|+(b+1)2=0,
∴a+2=0,b+1=0,
∴a=﹣2,b=﹣1,
∴a﹣b=﹣2+1=﹣1.
故选:B.
6.B
【解析】解:∵,
∴x+y=-22,
∴=20-(x+y)=20-(-22)=42,
故选B.
7.D
【解析】解:第1个图案中黑色小正方形地砖的块数为,
第2个图案中黑色小正方形地砖的块数为,
第3个图案中黑色小正方形地砖的块数为,
…
第n个图案中黑色小正方形地砖的块数为,
则第13个图案中黑色小正方形地砖的块数是.
故选:D
8.C
【解析】第1个图形中一共有5个,即1×(4+1),
第2个图形中一共有12个,即2×(4+2),
第3个图形中一共有21个,即3×(4+3),……,
∴第n个图形中“○”的个数是n×(4+n),
∴第7个图形中“○”的个数是7×(4+7)=77,
故选:C.
9.4
【解析】解:由题意得:x2+3x+5=7,即x2+3x=2,
则3x2+9x﹣2=3(x2+3x)-2=6-2=4,
故答案为:4.
10.
【解析】 a、b互为相反数,
,
故答案为:
11.2020
【解析】解:∵、互为相反数,、互为倒数
∴,,
则原式2020×1=2020,
故答案为:-2020.
12.-2
【解析】解:∵|a-1|≥0,|b+3|≥0,|a-1|+|b+3|=0,
∴a-1=0,b+3=0,
∴a=1,b=-3,
∴a+b=1-3=-2,
故答案为:-2.
13.1
【解析】解:根据题意得:+=0,
=0,=0,
解得:=-1,=2,
则原式= =1.
故答案为:1.
14.
【解析】解:;
;
;
;
……;
∴第n个数是:;
故答案:.
15.43
【解析】解:由|x|=x+2,显然|x|≠x,只能|x|= x,
得 x=x+2,
解得x= 1,
∴当x= 1时,
19+3+27=19×( 1)94+3×( 1)+27,
=19 3+27,
=43.
故本题答案为43.
16.
【解析】分子为b,指数为2,5,8,11,...,
分子指数的规律为3n – 1,
分母为a,指数为1,2,3,4,...,
分母指数的规律为n,
分数符号为-,+,-,+,….,
其规律为,
于是,第7个式子为,
第n个式子为,
故答案为:,.
17.7或-9
【解析】由题意得,,;
当时,
,
当时,
.
18.(1)-1或-5;(2)
【解析】(1)∵,,∴,,
若,则此时有两种情况:
,或,,
当,时,,
当,时,
综上的值为-1或-5.
(2)若,则有两种情况:
,或,,
当,时,,
当时,时,,
综上.
19.(1)﹣1;(2)5
【解析】解:(1)∵,
∴,,
∴,,
∴;
(2)∵,,
∴,,
∴.
20.
【解析】依题意得:
.
21.(1)7,12,17,22,27,32;(2)第n个图形需要根.
【解析】解:(1)由题意可知:图形①有7根,图形②有12根,图形③有17根,观察可以发现,后面一个图形比前面一个图形的火柴棒根数多5,
∴可以填表如下:
图形编号 ① ② ③ ④ ⑤ ⑥
火柴棒根数 7 12 17 22 27 32
(2)由(1)可知,后面一个图形比前面一个图形的火柴棒根数多5,
∴第n个图形需要的火柴棒根数,
∴第n个图形需要根火柴棒.
22.前四年树苗高度随着年数的增长而增长,树苗起始高度为100cm,随后每生长一年,树苗高度增加5cm,树苗生长了n年的高度为(100+5n)cm.
【解析】解:第一年,树苗高度为100+5×1=105(cm),
第二年,树苗高度为100+5×2=110(cm),
第三年,树苗高度为100+5×3=115(cm),
第四年,树苗高度为100+5×4=120(cm),
…
第n年,树苗高度为(100+5n)cm,
答:前四年树苗高度随着年数的增长而增长,树苗起始高度为100cm,随后每生长一年,树苗高度增加5cm,树苗生长了n年的高度为(100+5n)cm.
23.(1);(2)
【解析】解:(1)由观察知,左边:分子不变,为1;分母是两个连续奇数的乘积,它们与式子序号之间的关系为序号的2倍减1和序号的2倍加1,
右边:这两个奇数的倒数差的一半,
∴第5个式子是:;
故答案为:;×;
(2)由题意可得:.
故答案为:.
答案第1页,共2页
答案第1页,共2页
9.3代数式的值-同步练习
时间:60分钟
一、单选题
1.若|a+9|+(b﹣8)2=0,则(a+b)2021的值为( )
A.﹣1 B.0 C.1 D.2
2.规定,则的值为( )
A. B. C. D.
3.已知a=|﹣3|,则a﹣4=( )
A.﹣7 B.1 C.﹣1 D.﹣1或﹣7
4.当x=2与x=-2时,代数式x4-2x2+3的两个值( )
A.相等 B.互为倒数 C.互为相反数 D.既不相等也不互为相反数
5.|a+2|+(b+1)2=0,那么a-b的值是( )
A.1 B.﹣1 C.-3 D.3
6.若,则的值为( )
A.-42 B.42 C.-2 D.22
7.按照如图所示的方法排列黑色小正方形地砖,则第13个图案中黑色小正方形地砖的块数是( )
A.253 B.273 C.293 D.313
8.如图图形都是由同样大小的“○”按- -定的规律组成,其中第1个图形中一共有5个“○”,第2个图形中一共有12个“○”,第3个图形中一共有21个“○”,……,则第7个图形中“○”的个数是( )
A.60 B.66 C.77 D.96
二、填空题
9.当代数式x2+3x+5的值为7时,代数式3x2+9x﹣2的值是 ___.
10.若a、b互为相反数,则a+(b﹣2)的值为______________.
11.如果,互为相反数,,互为倒数,那么2020xy=_______.
12.若,则_____
13.若与互为相反数,则= _____.
14.观察一列数:,,,,,…,根据规律,第n个数是_______(用含n的代数式表示).
15.当||=+2时,19+3+27的值是______.
16.一组按规律排列的式子:,其中第7个式子是_______,第n个式子是_______(n为正整数).
三、解答题
17.已知a与b互为相反数,c与d互为倒数,m的绝对值为2,求式子﹣cd+m3的值.
18.已知,.
(1)若,求的值.
(2)若,求的值.
19.已知,试求:
(1)的值;
(2)的值.
20.如图,水压机有四根空心钢立柱,每根高都是,外径D为,内径d为.每立方米钢的质量为,求4根立柱的总质量(取3.14).
21.用火柴棒按下面的方式搭图形:
(1)填写下表:
图形编号 ① ② ③ ④ ⑤ ⑥
火柴棒根数
(2)第n个图形需要多少根火柴棒?
22.测得一种树苗的高度与树苗生长的年数的有关数据如下页表(树苗原高):
年数 高度/
1
2
3
4
…… ……
前四年树苗高度的变化与年数有什么关系?假设以后各年树苗高度的变化与年数保持上述关系,用式子表示生长了n年的树苗的高度.
23.分观察下列各式:
第个等式:;
第个等式:;
第个等式:;
第个等式:;
请回答下列各题:
(1)按以上规律列出第个等式: ;
(2)用含的式子表示第个等式(为正整数): .
试卷第1页,共3页
参考答案
1.A
【解析】解:由题意得,a+9=0,b-8=0,
解得a=-9,b=8,
所以,(a+b)2021=(-9+8)2021=(-1)2021=-1.
故答案为:A.
2.C
【解析】解:
已知:,
将,代入即为:
,
故选:C.
3.C
【解析】解:∵a=|﹣3|=3,
∴a﹣4=3-4=-1,
故选C.
4.A
【解析】解:当x=2时,
∴x4-2x2+3=24-2×22+3,
=16-8+3,
=11.
当x=-2时,
∴x4-2x2+3=(-2)4-2×(-2)2+3,
=16-8+3,
=11.
∴相等.
故答案为:A.
5.B
【解析】解:∵|a+2|+(b+1)2=0,
∴a+2=0,b+1=0,
∴a=﹣2,b=﹣1,
∴a﹣b=﹣2+1=﹣1.
故选:B.
6.B
【解析】解:∵,
∴x+y=-22,
∴=20-(x+y)=20-(-22)=42,
故选B.
7.D
【解析】解:第1个图案中黑色小正方形地砖的块数为,
第2个图案中黑色小正方形地砖的块数为,
第3个图案中黑色小正方形地砖的块数为,
…
第n个图案中黑色小正方形地砖的块数为,
则第13个图案中黑色小正方形地砖的块数是.
故选:D
8.C
【解析】第1个图形中一共有5个,即1×(4+1),
第2个图形中一共有12个,即2×(4+2),
第3个图形中一共有21个,即3×(4+3),……,
∴第n个图形中“○”的个数是n×(4+n),
∴第7个图形中“○”的个数是7×(4+7)=77,
故选:C.
9.4
【解析】解:由题意得:x2+3x+5=7,即x2+3x=2,
则3x2+9x﹣2=3(x2+3x)-2=6-2=4,
故答案为:4.
10.
【解析】 a、b互为相反数,
,
故答案为:
11.2020
【解析】解:∵、互为相反数,、互为倒数
∴,,
则原式2020×1=2020,
故答案为:-2020.
12.-2
【解析】解:∵|a-1|≥0,|b+3|≥0,|a-1|+|b+3|=0,
∴a-1=0,b+3=0,
∴a=1,b=-3,
∴a+b=1-3=-2,
故答案为:-2.
13.1
【解析】解:根据题意得:+=0,
=0,=0,
解得:=-1,=2,
则原式= =1.
故答案为:1.
14.
【解析】解:;
;
;
;
……;
∴第n个数是:;
故答案:.
15.43
【解析】解:由|x|=x+2,显然|x|≠x,只能|x|= x,
得 x=x+2,
解得x= 1,
∴当x= 1时,
19+3+27=19×( 1)94+3×( 1)+27,
=19 3+27,
=43.
故本题答案为43.
16.
【解析】分子为b,指数为2,5,8,11,...,
分子指数的规律为3n – 1,
分母为a,指数为1,2,3,4,...,
分母指数的规律为n,
分数符号为-,+,-,+,….,
其规律为,
于是,第7个式子为,
第n个式子为,
故答案为:,.
17.7或-9
【解析】由题意得,,;
当时,
,
当时,
.
18.(1)-1或-5;(2)
【解析】(1)∵,,∴,,
若,则此时有两种情况:
,或,,
当,时,,
当,时,
综上的值为-1或-5.
(2)若,则有两种情况:
,或,,
当,时,,
当时,时,,
综上.
19.(1)﹣1;(2)5
【解析】解:(1)∵,
∴,,
∴,,
∴;
(2)∵,,
∴,,
∴.
20.
【解析】依题意得:
.
21.(1)7,12,17,22,27,32;(2)第n个图形需要根.
【解析】解:(1)由题意可知:图形①有7根,图形②有12根,图形③有17根,观察可以发现,后面一个图形比前面一个图形的火柴棒根数多5,
∴可以填表如下:
图形编号 ① ② ③ ④ ⑤ ⑥
火柴棒根数 7 12 17 22 27 32
(2)由(1)可知,后面一个图形比前面一个图形的火柴棒根数多5,
∴第n个图形需要的火柴棒根数,
∴第n个图形需要根火柴棒.
22.前四年树苗高度随着年数的增长而增长,树苗起始高度为100cm,随后每生长一年,树苗高度增加5cm,树苗生长了n年的高度为(100+5n)cm.
【解析】解:第一年,树苗高度为100+5×1=105(cm),
第二年,树苗高度为100+5×2=110(cm),
第三年,树苗高度为100+5×3=115(cm),
第四年,树苗高度为100+5×4=120(cm),
…
第n年,树苗高度为(100+5n)cm,
答:前四年树苗高度随着年数的增长而增长,树苗起始高度为100cm,随后每生长一年,树苗高度增加5cm,树苗生长了n年的高度为(100+5n)cm.
23.(1);(2)
【解析】解:(1)由观察知,左边:分子不变,为1;分母是两个连续奇数的乘积,它们与式子序号之间的关系为序号的2倍减1和序号的2倍加1,
右边:这两个奇数的倒数差的一半,
∴第5个式子是:;
故答案为:;×;
(2)由题意可得:.
故答案为:.
答案第1页,共2页
答案第1页,共2页
