2021-2022学年人教A版必修一 2.1.2 指数函数及其性质 课件(24张)
文档属性
| 名称 | 2021-2022学年人教A版必修一 2.1.2 指数函数及其性质 课件(24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 08:18:12 | ||
图片预览








文档简介
(共24张PPT)
情景设计
传说古代印度有一个国王喜爱象棋,中国智者云游到此,国王得知智者棋艺高超,于是派人请来智者与其对弈,并且傲慢地说:“如果你赢了,我将答应你任何要求.”智者心想:我应治一治国王的傲慢,当国王输棋后,智者说:陛下只须派人用麦粒填满象棋上所有空格,第1格2粒,第2格4粒,第3格8粒, ……,以后每格是前一格粒数的2倍。国王说,这太简单了,吩咐手下马上去办,过了好多天,手下惊慌报告说:不好了。你猜怎样?原来经计算,印度近几十年的麦子加起来还不够。求格数与此格上麦粒数的关系。
情景设计
分析:
表达式:
由表达式知道,引起麦粒数y变化的是格数,而格数x出现在指数上,象这种自变量出现在指数上的函数就是指数函数。
此题即求第x格上麦粒数的个数y
研究:
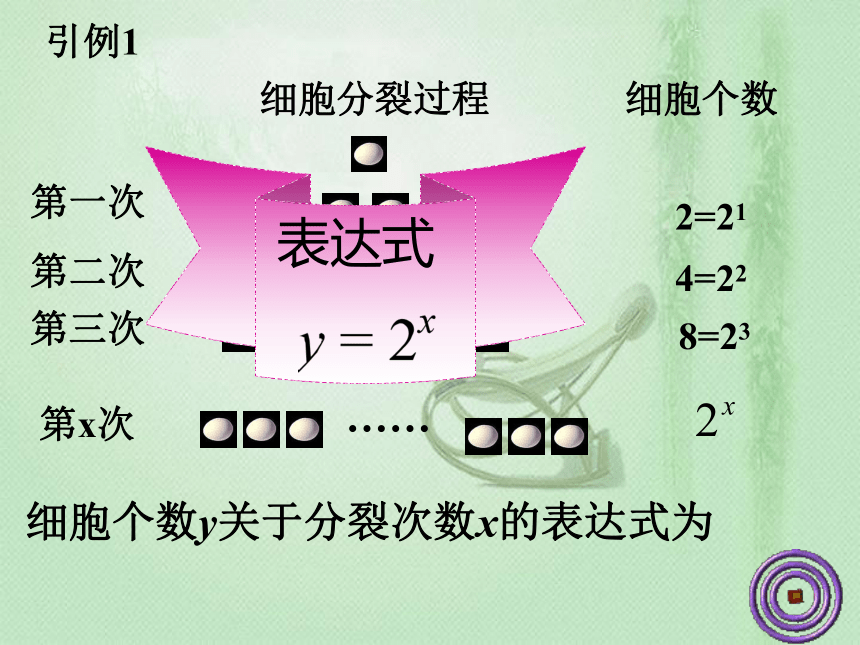
引例1:某种细胞分裂时,由1 个细胞分裂成2个,2个分裂成4个,......,一个这样的细胞分裂 x 次后,得到的细胞个数y与分裂次数x有怎样的函数关系?
引例2:某种商品的价格从今年起每年降低15设原来的价格为1,x年后的价格为y,则y与x的函数关系式?
引例1
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达式为
表达式
引例2:某种商品的价格从今年起每年降低15%,设
原来的价格为1,x年后的价格为y,则y与x的函数
关系式?
y
6
5
4
3
2
1
x
0.85
由上面的对应关系可知,函数关系是:
列表:
在
中指数x是自变量,
底数是一个大于0且不等于1的常量.
我们把这种自变量在指数位置上而底数是一个
大于0且不等于1的常量的函数叫做指数函数.
和
指数函数的定义:
函数
叫做指数函数,其中x是自变量,函数定义域是R。
探究1:为什么要规定a>0,且a
1呢?
0时,
①若a=0,则当x>0时,
=0;
无意义.
当x
②若a<0,则对于x的某些数值,可使
无意义.
如
,这时对于x=
,x=
……等等,在实数范围内函数值不存在.
③若a=1,则对于任何x
R,
=1,是一个常量,没有研究的必要性.
为了避免上述各种情况,所以规定a>0且a 1。
0
1
a
练习:
若
是一个指数函数,求a的取值范围。
解:由指数函数的定义可知,底数应该是大于0
且不等于1的常量。所以,
探究2:函数
是指数函数吗?
指数函数的解析式y=
中,
的系数是1.
有些函数看起来不像指数函数,实际上却是,如
因为它可以化为
有些函数貌似指数函数,实际上却不是,如
下列函数是否是指数函数:
练习2:
答案:(1) ,(2), (4)是指数函数。
x … -3 -2 -1 0 1 2 3 …
y=2x … 1/8 1/4 1 2 4 8 …
y=3x … 1/27 1/9 1/3 1 3 9 27 …
函 数 图 象 特 征
1
x
y
o
1
2
3
-1
-2
-3
x … -3 -2 -1 0 1 2 3 …
y=2-x … 8 4 2 1 1/2 1/4 1/8 …
y=3-x … 27 9 3 1 1/3 1/9 1/27 …
X
O
Y
Y=1
函 数 图 象 特 征
X
O
Y
Y=1
y=3X
y = 2 x
观察右边图象,回答下列问题:
问题一:
图象分别在哪几个象限?
问题二:
图象的上升、下降与底数a有联系吗?
问题三:
图象中有哪些特殊的点?
答四个图象都在第____象限。
答:当底数__ 时图象上升;当底数____时图象下降.
答:四个图象都经过点____.
Ⅰ、Ⅱ
X
O
Y
Y=1
y=3X
y = 2 x
观察右边图象,回答下列问题:
问题五:
函数 与 图象有
什么关系 ?
问题四:
指数函数 图像是否具有
对称性?
答:
关于Y轴对称。
答:
不关于Y轴对称不关于原点中心对称
当底数a
取任意值时,指数
函数图象是什么样?
指数函数的图象和性质
a>1 0图
象
x
y
0
y=1
y=ax
(a>1)
y
0
(0x
y=1
y=ax
(0,1)
a>1 0图
象
特
征
a>1 0性
质
1.图象全在x轴上方,与x轴无限接近.
1.定义域为R,值域为(0,+ ).
2.图象过定点(0,1)
2.当x=0时,y=1
3.自左向右图象逐渐上升
3.自左向右图象逐渐下降
3.在R上是增函数
3.在R上是减函数
4.图象分布在左下和右上两个区域内
4.图象分布在左上和右下两个区域内
4.当x>0时,y>1;当x<0时,04.当x>0时, 01.
非奇非偶函数
不关于Y轴对称不关于原点中心对称
例1、求下列函数的定义域:
解:
①
②
①
②
应用示例:
应用示例:
例2已知指数函数
经过点(3,π),求
f(0)、f(1)、f(-3)的值.
(a>0,且a≠1)的图象
反思:
你能说出确定一个指数函数需要什么
条件吗?
提高练习:
求函数的定义域:
小结:
函数
叫做指数函数,其中x是自变量,函数定义域是R。
1.指数函数的定义:
a>1 0图
象
性
质 1.定义域:R
2.值域:(0,+∞)
3.过点(0,1),即x=0时,y=1
4.在 R上是增函数 在R上是减函数
2.指数函数的的图象和性质:
方法:利用函数图像研究函数性质是一种直观而形象的
方法,记忆指数函数性质时可以联想指数函数的图像。
课后作业:
5、6.
习题2.1A
必做题:
选做题:
习题2.1B 1
情景设计
传说古代印度有一个国王喜爱象棋,中国智者云游到此,国王得知智者棋艺高超,于是派人请来智者与其对弈,并且傲慢地说:“如果你赢了,我将答应你任何要求.”智者心想:我应治一治国王的傲慢,当国王输棋后,智者说:陛下只须派人用麦粒填满象棋上所有空格,第1格2粒,第2格4粒,第3格8粒, ……,以后每格是前一格粒数的2倍。国王说,这太简单了,吩咐手下马上去办,过了好多天,手下惊慌报告说:不好了。你猜怎样?原来经计算,印度近几十年的麦子加起来还不够。求格数与此格上麦粒数的关系。
情景设计
分析:
表达式:
由表达式知道,引起麦粒数y变化的是格数,而格数x出现在指数上,象这种自变量出现在指数上的函数就是指数函数。
此题即求第x格上麦粒数的个数y
研究:
引例1:某种细胞分裂时,由1 个细胞分裂成2个,2个分裂成4个,......,一个这样的细胞分裂 x 次后,得到的细胞个数y与分裂次数x有怎样的函数关系?
引例2:某种商品的价格从今年起每年降低15设原来的价格为1,x年后的价格为y,则y与x的函数关系式?
引例1
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达式为
表达式
引例2:某种商品的价格从今年起每年降低15%,设
原来的价格为1,x年后的价格为y,则y与x的函数
关系式?
y
6
5
4
3
2
1
x
0.85
由上面的对应关系可知,函数关系是:
列表:
在
中指数x是自变量,
底数是一个大于0且不等于1的常量.
我们把这种自变量在指数位置上而底数是一个
大于0且不等于1的常量的函数叫做指数函数.
和
指数函数的定义:
函数
叫做指数函数,其中x是自变量,函数定义域是R。
探究1:为什么要规定a>0,且a
1呢?
0时,
①若a=0,则当x>0时,
=0;
无意义.
当x
②若a<0,则对于x的某些数值,可使
无意义.
如
,这时对于x=
,x=
……等等,在实数范围内函数值不存在.
③若a=1,则对于任何x
R,
=1,是一个常量,没有研究的必要性.
为了避免上述各种情况,所以规定a>0且a 1。
0
1
a
练习:
若
是一个指数函数,求a的取值范围。
解:由指数函数的定义可知,底数应该是大于0
且不等于1的常量。所以,
探究2:函数
是指数函数吗?
指数函数的解析式y=
中,
的系数是1.
有些函数看起来不像指数函数,实际上却是,如
因为它可以化为
有些函数貌似指数函数,实际上却不是,如
下列函数是否是指数函数:
练习2:
答案:(1) ,(2), (4)是指数函数。
x … -3 -2 -1 0 1 2 3 …
y=2x … 1/8 1/4 1 2 4 8 …
y=3x … 1/27 1/9 1/3 1 3 9 27 …
函 数 图 象 特 征
1
x
y
o
1
2
3
-1
-2
-3
x … -3 -2 -1 0 1 2 3 …
y=2-x … 8 4 2 1 1/2 1/4 1/8 …
y=3-x … 27 9 3 1 1/3 1/9 1/27 …
X
O
Y
Y=1
函 数 图 象 特 征
X
O
Y
Y=1
y=3X
y = 2 x
观察右边图象,回答下列问题:
问题一:
图象分别在哪几个象限?
问题二:
图象的上升、下降与底数a有联系吗?
问题三:
图象中有哪些特殊的点?
答四个图象都在第____象限。
答:当底数__ 时图象上升;当底数____时图象下降.
答:四个图象都经过点____.
Ⅰ、Ⅱ
X
O
Y
Y=1
y=3X
y = 2 x
观察右边图象,回答下列问题:
问题五:
函数 与 图象有
什么关系 ?
问题四:
指数函数 图像是否具有
对称性?
答:
关于Y轴对称。
答:
不关于Y轴对称不关于原点中心对称
当底数a
取任意值时,指数
函数图象是什么样?
指数函数的图象和性质
a>1 0
象
x
y
0
y=1
y=ax
(a>1)
y
0
(0
y=1
y=ax
(0,1)
a>1 0
象
特
征
a>1 0
质
1.图象全在x轴上方,与x轴无限接近.
1.定义域为R,值域为(0,+ ).
2.图象过定点(0,1)
2.当x=0时,y=1
3.自左向右图象逐渐上升
3.自左向右图象逐渐下降
3.在R上是增函数
3.在R上是减函数
4.图象分布在左下和右上两个区域内
4.图象分布在左上和右下两个区域内
4.当x>0时,y>1;当x<0时,0
非奇非偶函数
不关于Y轴对称不关于原点中心对称
例1、求下列函数的定义域:
解:
①
②
①
②
应用示例:
应用示例:
例2已知指数函数
经过点(3,π),求
f(0)、f(1)、f(-3)的值.
(a>0,且a≠1)的图象
反思:
你能说出确定一个指数函数需要什么
条件吗?
提高练习:
求函数的定义域:
小结:
函数
叫做指数函数,其中x是自变量,函数定义域是R。
1.指数函数的定义:
a>1 0
象
性
质 1.定义域:R
2.值域:(0,+∞)
3.过点(0,1),即x=0时,y=1
4.在 R上是增函数 在R上是减函数
2.指数函数的的图象和性质:
方法:利用函数图像研究函数性质是一种直观而形象的
方法,记忆指数函数性质时可以联想指数函数的图像。
课后作业:
5、6.
习题2.1A
必做题:
选做题:
习题2.1B 1
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
