2021-2022学年上学期高二数学人教A版(2019)3.3《抛物线及其标准方程》课件(共29张PPT)
文档属性
| 名称 | 2021-2022学年上学期高二数学人教A版(2019)3.3《抛物线及其标准方程》课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 15:55:23 | ||
图片预览








文档简介
(共29张PPT)
平面内与定点的距离和一条定直线的距离之比为一个常数e的点的轨迹是什么?
思考
一
情境设置
0e>1时,轨迹是双曲线。
平面内与定点的距离和一条定直线的距离之比为一个常数e的点的轨迹是什么?
思考
一
情境设置
平面内与定点的距离和一条定直线的距离之比为一个常数e的点的轨迹是什么?
那么,e=1时,轨迹是什么呢?
思考
一
情境设置
信息技术应用
一
情境设置
1. 抛物线的定义
我们把平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线, 点F叫做抛物线的焦点, 直线l叫做抛物线的准线.
【注】点F不在直线l上。
二
新知探究
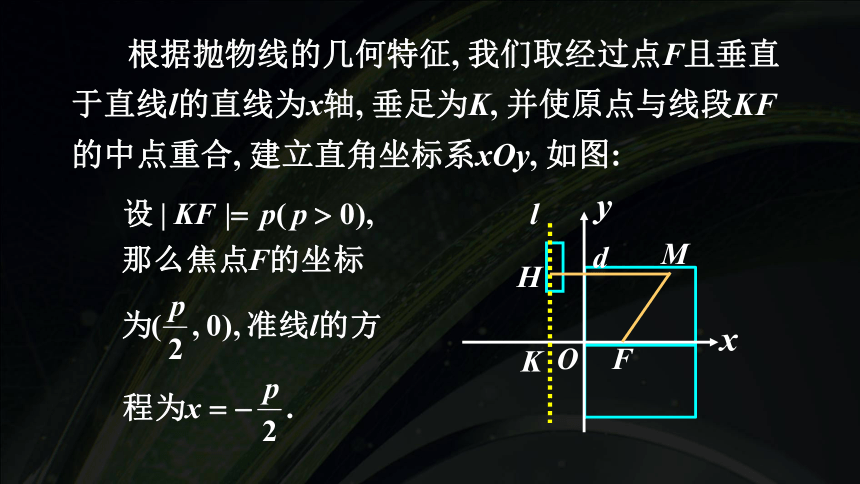
根据抛物线的几何特征, 我们取经过点F且垂直于直线l的直线为x轴, 垂足为K, 并使原点与线段KF的中点重合, 建立直角坐标系xOy, 如图:
探究
图形 标准方程 焦点坐标 准线方程
图形 标准方程 焦点坐标 准线方程
图形 标准方程 焦点坐标 准线方程
图形 标准方程 焦点坐标 准线方程
你能说明二次函数 y=ax2(a≠0)的图象为什么是抛物线吗?指出它的焦点坐标、准线方程。
思考
你能说明二次函数 y=ax2(a≠0)的图象为什么是抛物线吗?指出它的焦点坐标、准线方程。
焦点为 ,
思考
你能说明二次函数 y=ax2(a≠0)的图象为什么是抛物线吗?指出它的焦点坐标、准线方程。
焦点为 ,
准线方程为
思考
(1) 已知抛物线的标准方程y2=6x, 求它的焦点坐标和准线方程.
(2) 已知抛物线的焦点坐标是F(0, -2),求它的准线和标准方程.
一种卫星接收天线的轴截面如图所示.卫星波束呈近似平行状态射入轴截面为抛物线的接收天线, 经反射聚集到焦点处. 已知接收天线的口径(直径)为4.8m, 深度为0.5m.试建立适当的坐标系, 求抛物线的标准方程和焦点坐标.
【例2】
一种卫星接收天线的轴截面如图所示.卫星波束呈近似平行状态射入轴截面为抛物线的接收天线, 经反射聚集到焦点处. 已知接收天线的口径(直径)为4.8m, 深度为0.5m.试建立适当的坐标系, 求抛物线的标准方程和焦点坐标.
x
O
y
A
B
F
【例2】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
【例3】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
A
O
F
x
y
P
【例3】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
A
O
F
x
y
P
【例3】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
A
O
F
x
y
P
B
【例3】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
A
O
F
x
y
P
B
M
【例3】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
A
O
F
x
y
P
B
M
点P(2, 2), 最小值为 .
【例3】
抛物线 x2=4y上一点M到焦点距离是3,求点M的坐标。
【例4】
抛物线的标准方程有四种形式,并且二次项系数为1,一次项及其系数的符号能确定抛物线的开口方向,一次项系数的1/4是焦点的非零坐标值.
三
课堂总结
《考一本》第17课时
四
作业布置
平面内与定点的距离和一条定直线的距离之比为一个常数e的点的轨迹是什么?
思考
一
情境设置
0
平面内与定点的距离和一条定直线的距离之比为一个常数e的点的轨迹是什么?
思考
一
情境设置
平面内与定点的距离和一条定直线的距离之比为一个常数e的点的轨迹是什么?
那么,e=1时,轨迹是什么呢?
思考
一
情境设置
信息技术应用
一
情境设置
1. 抛物线的定义
我们把平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线, 点F叫做抛物线的焦点, 直线l叫做抛物线的准线.
【注】点F不在直线l上。
二
新知探究
根据抛物线的几何特征, 我们取经过点F且垂直于直线l的直线为x轴, 垂足为K, 并使原点与线段KF的中点重合, 建立直角坐标系xOy, 如图:
探究
图形 标准方程 焦点坐标 准线方程
图形 标准方程 焦点坐标 准线方程
图形 标准方程 焦点坐标 准线方程
图形 标准方程 焦点坐标 准线方程
你能说明二次函数 y=ax2(a≠0)的图象为什么是抛物线吗?指出它的焦点坐标、准线方程。
思考
你能说明二次函数 y=ax2(a≠0)的图象为什么是抛物线吗?指出它的焦点坐标、准线方程。
焦点为 ,
思考
你能说明二次函数 y=ax2(a≠0)的图象为什么是抛物线吗?指出它的焦点坐标、准线方程。
焦点为 ,
准线方程为
思考
(1) 已知抛物线的标准方程y2=6x, 求它的焦点坐标和准线方程.
(2) 已知抛物线的焦点坐标是F(0, -2),求它的准线和标准方程.
一种卫星接收天线的轴截面如图所示.卫星波束呈近似平行状态射入轴截面为抛物线的接收天线, 经反射聚集到焦点处. 已知接收天线的口径(直径)为4.8m, 深度为0.5m.试建立适当的坐标系, 求抛物线的标准方程和焦点坐标.
【例2】
一种卫星接收天线的轴截面如图所示.卫星波束呈近似平行状态射入轴截面为抛物线的接收天线, 经反射聚集到焦点处. 已知接收天线的口径(直径)为4.8m, 深度为0.5m.试建立适当的坐标系, 求抛物线的标准方程和焦点坐标.
x
O
y
A
B
F
【例2】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
【例3】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
A
O
F
x
y
P
【例3】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
A
O
F
x
y
P
【例3】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
A
O
F
x
y
P
B
【例3】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
A
O
F
x
y
P
B
M
【例3】
设点P为抛物线 y2=2x上一动点,点F为抛物线的焦点,点A(3, 2)为定点,当点P在何位置时,|PF|+|PA|取最小值?并求其最小值.
A
O
F
x
y
P
B
M
点P(2, 2), 最小值为 .
【例3】
抛物线 x2=4y上一点M到焦点距离是3,求点M的坐标。
【例4】
抛物线的标准方程有四种形式,并且二次项系数为1,一次项及其系数的符号能确定抛物线的开口方向,一次项系数的1/4是焦点的非零坐标值.
三
课堂总结
《考一本》第17课时
四
作业布置
