2021-2022学年上学期高二数学人教A版(2019)《数列的概念及简单表示法》课件(共51张PPT)
文档属性
| 名称 | 2021-2022学年上学期高二数学人教A版(2019)《数列的概念及简单表示法》课件(共51张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 15:57:19 | ||
图片预览





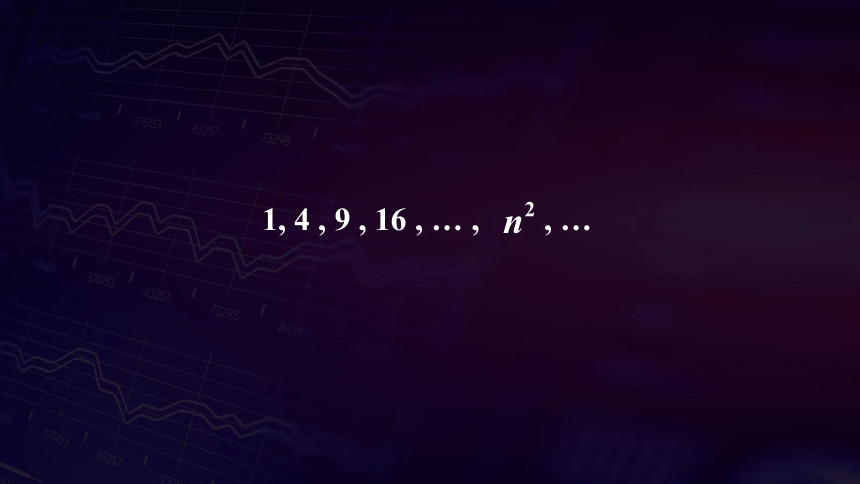


文档简介
(共51张PPT)
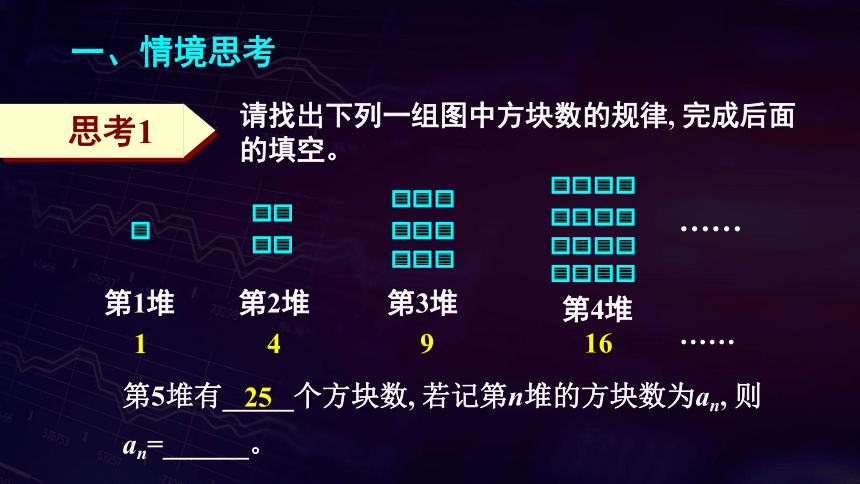
一、情境思考
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an=______。
第1堆
第2堆
第3堆
第4堆
……
思考1
一、情境思考
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an=______。
第1堆
第2堆
第3堆
第4堆
……
1
4
9
16
……
思考1
一、情境思考
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an=______。
第1堆
第2堆
第3堆
第4堆
……
1
4
9
16
25
……
思考1
一、情境思考
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an=______。
第1堆
第2堆
第3堆
第4堆
……
1
4
9
16
25
……
思考1
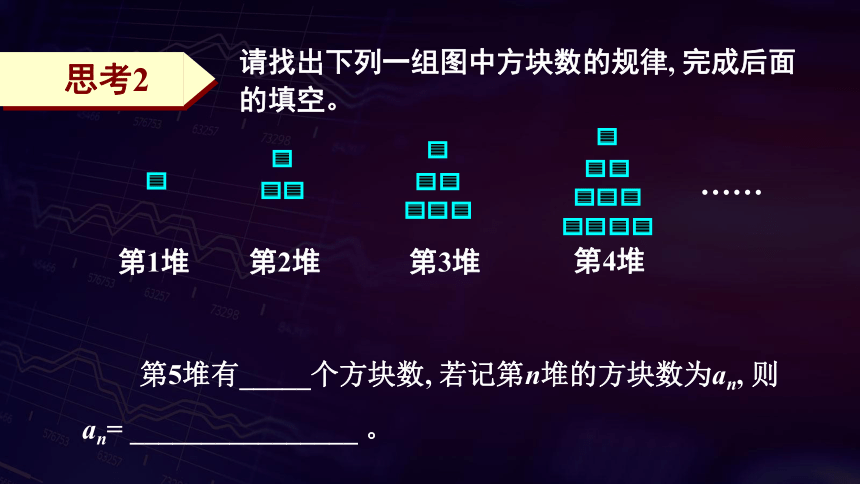
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an= ________________ 。
第1堆
第2堆
第3堆
第4堆
……
思考2
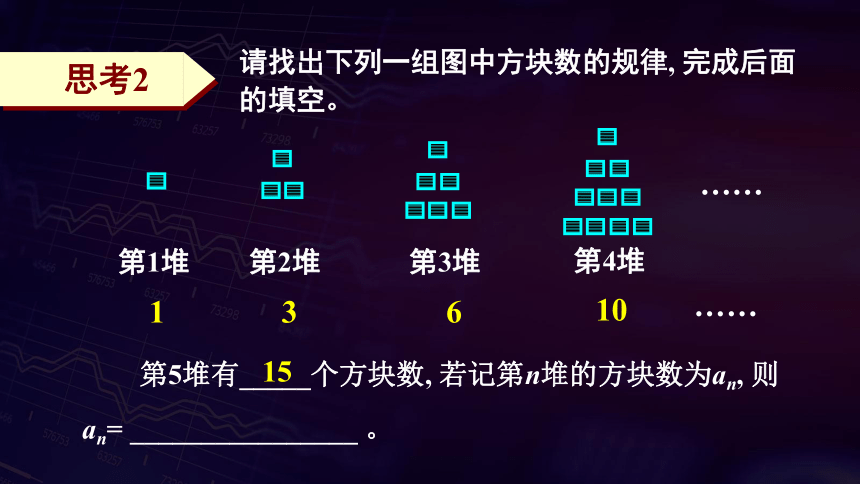
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an= ________________ 。
第1堆
第2堆
第3堆
第4堆
……
1
3
6
10
……
思考2
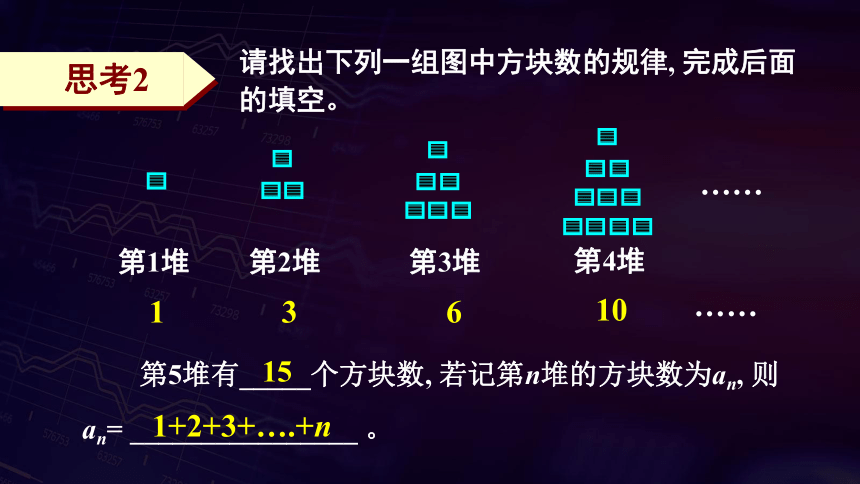
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an= ________________ 。
第1堆
第2堆
第3堆
第4堆
……
1
3
6
10
15
……
思考2
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an= ________________ 。
第1堆
第2堆
第3堆
第4堆
……
1
3
6
10
15
1+2+3+….+n
……
思考2
1, 4 , 9 , 16 , … , , …
(1)数列:
1, 4 , 9 , 16 , … , , …
按照一定顺序排列的一列数
(1)数列:
1, 4 , 9 , 16 , … , , …
按照一定顺序排列的一列数
(1)数列:
1, 4 , 9 , 16 , … , , …
0, 2, 4, 6, 8与8, 6,4, 2, 0是同一个数列. ( )
按照一定顺序排列的一列数
(1)数列:
1, 4 , 9 , 16 , … , , …
0, 2, 4, 6, 8与8, 6,4, 2, 0是同一个数列. ( )
×
按照一定顺序排列的一列数
(1)数列:
1, 4 , 9 , 16 , … , , …
(2)数列的项:
按照一定顺序排列的一列数
(1)数列:
1, 4 , 9 , 16 , … , , …
(2)数列的项:
按照一定顺序排列的一列数
数列中的每一个数
(1)数列:
1, 4 , 9 , 16 , … , , …
(2)数列的项:
按照一定顺序排列的一列数
数列中的每一个数
(1)数列:
首项
1, 4 , 9 , 16 , … , , …
(2)数列的项:
按照一定顺序排列的一列数
数列中的每一个数
(1)数列:
首项
1, 4 , 9 , 16 , … , , …
通项
(2)数列的项:
按照一定顺序排列的一列数
数列中的每一个数
(1)数列:
首项
(3)数列的一般形式:
1, 4 , 9 , 16 , … , , …
通项
(2)数列的项:
按照一定顺序排列的一列数
数列中的每一个数
a1, a2, a3,…,an,…,
简记为{an}。
(1)数列:
首项
(3)数列的一般形式:
1, 4 , 9 , 16 , … , , …
通项
1、按照项数多少不同分类
(4) 有穷数列:
项数有限的数列
1、按照项数多少不同分类
(4) 有穷数列:
(5) 无穷数列:
项数有限的数列
项数无限的数列
1、按照项数多少不同分类
(4) 有穷数列:
(5) 无穷数列:
项数有限的数列
项数无限的数列
1、按照项数多少不同分类
2、按照数列中各项大小的变化规律分类:
(4) 有穷数列:
(5) 无穷数列:
项数有限的数列
项数无限的数列
从第二项开始,每一项大(小)于它的前一项的数列叫做递增(减)数列
(6) 递增(减)数列:
1、按照项数多少不同分类
2、按照数列中各项大小的变化规律分类:
(4) 有穷数列:
(5) 无穷数列:
项数有限的数列
项数无限的数列
从第二项开始,每一项大(小)于它的前一项的数列叫做递增(减)数列
各项相等的数列叫做常数列
(7) 常数列:
(6) 递增(减)数列:
1、按照项数多少不同分类
2、按照数列中各项大小的变化规律分类:
(4) 有穷数列:
(5) 无穷数列:
项数有限的数列
项数无限的数列
(8) 摆动数列:
从第二项开始,每一项大(小)于它的前一项的数列叫做递增(减)数列
各项相等的数列叫做常数列
从第二项开始,有一些项大于它的前一项,有些项小于它的前一项的数列叫做摆动数列
(7) 常数列:
(6) 递增(减)数列:
1、按照项数多少不同分类
2、按照数列中各项大小的变化规律分类:
正方形数:1 , 4 , 9 , 16 , 25 , ……
1 4 9 … …
第1项 第2项 第3项 … 第n项 …
二、新知探究
正方形数:1 , 4 , 9 , 16 , 25 , ……
1 4 9 … …
思考:数列和函数有什么关系?
第1项 第2项 第3项 … 第n项 …
二、新知探究
正方形数:1 , 4 , 9 , 16 , 25 , ……
1 4 9 … …
思考:数列和函数有什么关系?
第1项 第2项 第3项 … 第n项 …
n
f(n)
二、新知探究
结论:
(1) 数列 函数
结论:
数列可以看成以正整数集或它的有限子集{1,2,…n}为定义域的函数 当自变量按照从小到大的顺序依次对应的一列函数值。
(1) 数列 函数
结论:
数列可以看成以正整数集或它的有限子集{1,2,…n}为定义域的函数 当自变量按照从小到大的顺序依次对应的一列函数值。
(1) 数列 函数
(2) 函 数 数列
结论:
对于函数 ,如果 有意义,可得到一个数列
数列可以看成以正整数集或它的有限子集{1,2,…n}为定义域的函数 当自变量按照从小到大的顺序依次对应的一列函数值。
(1) 数列 函数
(2) 函 数 数列
通项公式:
如果 数列 的第n项与序号n之间关系可以用一个式子表示,则这个公式叫数列的通项公式。
数列的表示法
通项公式:
如果 数列 的第n项与序号n之间关系可以用一个式子表示,则这个公式叫数列的通项公式。
数列的表示法
如正方形数通项公式 an =n2
通项公式:
如果 数列 的第n项与序号n之间关系可以用一个式子表示,则这个公式叫数列的通项公式。
数列的表示法
如三角形数通项公式 an =1+2+…+n
如正方形数通项公式 an =n2
判断下面的数列哪些有限或者无限,哪些是递增数列、递减数列、常数列、摆动数列?
(1)全体自然数构成集合:0,1,2,3,4……
(2)1996~2002年某市普通高中生人数(单位:万人)构成数列:82,93,105,119,129,130,132.
(3)无穷多个3构成数列:3,3,3,3……
【例1】
判断下面的数列哪些有限或者无限,哪些是递增数列、递减数列、常数列、摆动数列?
(1)全体自然数构成集合:0,1,2,3,4……
(2)1996~2002年某市普通高中生人数(单位:万人)构成数列:82,93,105,119,129,130,132.
(3)无穷多个3构成数列:3,3,3,3……
无限、递增
【例1】
判断下面的数列哪些有限或者无限,哪些是递增数列、递减数列、常数列、摆动数列?
(1)全体自然数构成集合:0,1,2,3,4……
(2)1996~2002年某市普通高中生人数(单位:万人)构成数列:82,93,105,119,129,130,132.
(3)无穷多个3构成数列:3,3,3,3……
无限、递增
有限、递增
【例1】
判断下面的数列哪些有限或者无限,哪些是递增数列、递减数列、常数列、摆动数列?
(1)全体自然数构成集合:0,1,2,3,4……
(2)1996~2002年某市普通高中生人数(单位:万人)构成数列:82,93,105,119,129,130,132.
(3)无穷多个3构成数列:3,3,3,3……
无限、递增
有限、递增
无限、常数列
【例1】
(4)目前通用的人民币面额按从大到小的顺序构成数列(单位:元):100 , 50 , 20 , 10 , 5 , 2 , 1 , 0.5 , 0.2 , 0.1 , 0.05 , 0.02 , 0.01.
(6) 精确到1,0.1,0.01,0.001……的不足近似值与过剩近似值分别构成数列:
1,1.4, 1.41, 1.414, ……
2, 1.5, 1.43, 1.415, ……
(5)-1的1次幂,2次幂,3次幂,4次幂:
-1, 1 ,-1 , 1,……
(4)目前通用的人民币面额按从大到小的顺序构成数列(单位:元):100 , 50 , 20 , 10 , 5 , 2 , 1 , 0.5 , 0.2 , 0.1 , 0.05 , 0.02 , 0.01.
(6) 精确到1,0.1,0.01,0.001……的不足近似值与过剩近似值分别构成数列:
1,1.4, 1.41, 1.414, ……
2, 1.5, 1.43, 1.415, ……
有限、递减
(5)-1的1次幂,2次幂,3次幂,4次幂:
-1, 1 ,-1 , 1,……
(4)目前通用的人民币面额按从大到小的顺序构成数列(单位:元):100 , 50 , 20 , 10 , 5 , 2 , 1 , 0.5 , 0.2 , 0.1 , 0.05 , 0.02 , 0.01.
(6) 精确到1,0.1,0.01,0.001……的不足近似值与过剩近似值分别构成数列:
1,1.4, 1.41, 1.414, ……
2, 1.5, 1.43, 1.415, ……
有限、递减
无限、摆动
(5)-1的1次幂,2次幂,3次幂,4次幂:
-1, 1 ,-1 , 1,……
(4)目前通用的人民币面额按从大到小的顺序构成数列(单位:元):100 , 50 , 20 , 10 , 5 , 2 , 1 , 0.5 , 0.2 , 0.1 , 0.05 , 0.02 , 0.01.
(6) 精确到1,0.1,0.01,0.001……的不足近似值与过剩近似值分别构成数列:
1,1.4, 1.41, 1.414, ……
2, 1.5, 1.43, 1.415, ……
有限、递减
无限、摆动
无限、递增
(5)-1的1次幂,2次幂,3次幂,4次幂:
-1, 1 ,-1 , 1,……
(4)目前通用的人民币面额按从大到小的顺序构成数列(单位:元):100 , 50 , 20 , 10 , 5 , 2 , 1 , 0.5 , 0.2 , 0.1 , 0.05 , 0.02 , 0.01.
(6) 精确到1,0.1,0.01,0.001……的不足近似值与过剩近似值分别构成数列:
1,1.4, 1.41, 1.414, ……
2, 1.5, 1.43, 1.415, ……
有限、递减
无限、摆动
无限、递增
无限、递减
(5)-1的1次幂,2次幂,3次幂,4次幂:
-1, 1 ,-1 , 1,……
写出下列数列的一个通项公式。
三、例题精析
【例2】
变式. 写出下列数列的一个通项公式。
探究2:若数列{an}的通项公式为an=-2n2+15n+5, 则数列中最大的一项是第____项,值为_________。
探究2:若数列{an}的通项公式为an=-2n2+15n+5, 则数列中最大的一项是第____项,值为_________。
4
33
一、情境思考
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an=______。
第1堆
第2堆
第3堆
第4堆
……
思考1
一、情境思考
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an=______。
第1堆
第2堆
第3堆
第4堆
……
1
4
9
16
……
思考1
一、情境思考
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an=______。
第1堆
第2堆
第3堆
第4堆
……
1
4
9
16
25
……
思考1
一、情境思考
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an=______。
第1堆
第2堆
第3堆
第4堆
……
1
4
9
16
25
……
思考1
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an= ________________ 。
第1堆
第2堆
第3堆
第4堆
……
思考2
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an= ________________ 。
第1堆
第2堆
第3堆
第4堆
……
1
3
6
10
……
思考2
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an= ________________ 。
第1堆
第2堆
第3堆
第4堆
……
1
3
6
10
15
……
思考2
请找出下列一组图中方块数的规律, 完成后面的填空。
第5堆有_____个方块数, 若记第n堆的方块数为an, 则an= ________________ 。
第1堆
第2堆
第3堆
第4堆
……
1
3
6
10
15
1+2+3+….+n
……
思考2
1, 4 , 9 , 16 , … , , …
(1)数列:
1, 4 , 9 , 16 , … , , …
按照一定顺序排列的一列数
(1)数列:
1, 4 , 9 , 16 , … , , …
按照一定顺序排列的一列数
(1)数列:
1, 4 , 9 , 16 , … , , …
0, 2, 4, 6, 8与8, 6,4, 2, 0是同一个数列. ( )
按照一定顺序排列的一列数
(1)数列:
1, 4 , 9 , 16 , … , , …
0, 2, 4, 6, 8与8, 6,4, 2, 0是同一个数列. ( )
×
按照一定顺序排列的一列数
(1)数列:
1, 4 , 9 , 16 , … , , …
(2)数列的项:
按照一定顺序排列的一列数
(1)数列:
1, 4 , 9 , 16 , … , , …
(2)数列的项:
按照一定顺序排列的一列数
数列中的每一个数
(1)数列:
1, 4 , 9 , 16 , … , , …
(2)数列的项:
按照一定顺序排列的一列数
数列中的每一个数
(1)数列:
首项
1, 4 , 9 , 16 , … , , …
(2)数列的项:
按照一定顺序排列的一列数
数列中的每一个数
(1)数列:
首项
1, 4 , 9 , 16 , … , , …
通项
(2)数列的项:
按照一定顺序排列的一列数
数列中的每一个数
(1)数列:
首项
(3)数列的一般形式:
1, 4 , 9 , 16 , … , , …
通项
(2)数列的项:
按照一定顺序排列的一列数
数列中的每一个数
a1, a2, a3,…,an,…,
简记为{an}。
(1)数列:
首项
(3)数列的一般形式:
1, 4 , 9 , 16 , … , , …
通项
1、按照项数多少不同分类
(4) 有穷数列:
项数有限的数列
1、按照项数多少不同分类
(4) 有穷数列:
(5) 无穷数列:
项数有限的数列
项数无限的数列
1、按照项数多少不同分类
(4) 有穷数列:
(5) 无穷数列:
项数有限的数列
项数无限的数列
1、按照项数多少不同分类
2、按照数列中各项大小的变化规律分类:
(4) 有穷数列:
(5) 无穷数列:
项数有限的数列
项数无限的数列
从第二项开始,每一项大(小)于它的前一项的数列叫做递增(减)数列
(6) 递增(减)数列:
1、按照项数多少不同分类
2、按照数列中各项大小的变化规律分类:
(4) 有穷数列:
(5) 无穷数列:
项数有限的数列
项数无限的数列
从第二项开始,每一项大(小)于它的前一项的数列叫做递增(减)数列
各项相等的数列叫做常数列
(7) 常数列:
(6) 递增(减)数列:
1、按照项数多少不同分类
2、按照数列中各项大小的变化规律分类:
(4) 有穷数列:
(5) 无穷数列:
项数有限的数列
项数无限的数列
(8) 摆动数列:
从第二项开始,每一项大(小)于它的前一项的数列叫做递增(减)数列
各项相等的数列叫做常数列
从第二项开始,有一些项大于它的前一项,有些项小于它的前一项的数列叫做摆动数列
(7) 常数列:
(6) 递增(减)数列:
1、按照项数多少不同分类
2、按照数列中各项大小的变化规律分类:
正方形数:1 , 4 , 9 , 16 , 25 , ……
1 4 9 … …
第1项 第2项 第3项 … 第n项 …
二、新知探究
正方形数:1 , 4 , 9 , 16 , 25 , ……
1 4 9 … …
思考:数列和函数有什么关系?
第1项 第2项 第3项 … 第n项 …
二、新知探究
正方形数:1 , 4 , 9 , 16 , 25 , ……
1 4 9 … …
思考:数列和函数有什么关系?
第1项 第2项 第3项 … 第n项 …
n
f(n)
二、新知探究
结论:
(1) 数列 函数
结论:
数列可以看成以正整数集或它的有限子集{1,2,…n}为定义域的函数 当自变量按照从小到大的顺序依次对应的一列函数值。
(1) 数列 函数
结论:
数列可以看成以正整数集或它的有限子集{1,2,…n}为定义域的函数 当自变量按照从小到大的顺序依次对应的一列函数值。
(1) 数列 函数
(2) 函 数 数列
结论:
对于函数 ,如果 有意义,可得到一个数列
数列可以看成以正整数集或它的有限子集{1,2,…n}为定义域的函数 当自变量按照从小到大的顺序依次对应的一列函数值。
(1) 数列 函数
(2) 函 数 数列
通项公式:
如果 数列 的第n项与序号n之间关系可以用一个式子表示,则这个公式叫数列的通项公式。
数列的表示法
通项公式:
如果 数列 的第n项与序号n之间关系可以用一个式子表示,则这个公式叫数列的通项公式。
数列的表示法
如正方形数通项公式 an =n2
通项公式:
如果 数列 的第n项与序号n之间关系可以用一个式子表示,则这个公式叫数列的通项公式。
数列的表示法
如三角形数通项公式 an =1+2+…+n
如正方形数通项公式 an =n2
判断下面的数列哪些有限或者无限,哪些是递增数列、递减数列、常数列、摆动数列?
(1)全体自然数构成集合:0,1,2,3,4……
(2)1996~2002年某市普通高中生人数(单位:万人)构成数列:82,93,105,119,129,130,132.
(3)无穷多个3构成数列:3,3,3,3……
【例1】
判断下面的数列哪些有限或者无限,哪些是递增数列、递减数列、常数列、摆动数列?
(1)全体自然数构成集合:0,1,2,3,4……
(2)1996~2002年某市普通高中生人数(单位:万人)构成数列:82,93,105,119,129,130,132.
(3)无穷多个3构成数列:3,3,3,3……
无限、递增
【例1】
判断下面的数列哪些有限或者无限,哪些是递增数列、递减数列、常数列、摆动数列?
(1)全体自然数构成集合:0,1,2,3,4……
(2)1996~2002年某市普通高中生人数(单位:万人)构成数列:82,93,105,119,129,130,132.
(3)无穷多个3构成数列:3,3,3,3……
无限、递增
有限、递增
【例1】
判断下面的数列哪些有限或者无限,哪些是递增数列、递减数列、常数列、摆动数列?
(1)全体自然数构成集合:0,1,2,3,4……
(2)1996~2002年某市普通高中生人数(单位:万人)构成数列:82,93,105,119,129,130,132.
(3)无穷多个3构成数列:3,3,3,3……
无限、递增
有限、递增
无限、常数列
【例1】
(4)目前通用的人民币面额按从大到小的顺序构成数列(单位:元):100 , 50 , 20 , 10 , 5 , 2 , 1 , 0.5 , 0.2 , 0.1 , 0.05 , 0.02 , 0.01.
(6) 精确到1,0.1,0.01,0.001……的不足近似值与过剩近似值分别构成数列:
1,1.4, 1.41, 1.414, ……
2, 1.5, 1.43, 1.415, ……
(5)-1的1次幂,2次幂,3次幂,4次幂:
-1, 1 ,-1 , 1,……
(4)目前通用的人民币面额按从大到小的顺序构成数列(单位:元):100 , 50 , 20 , 10 , 5 , 2 , 1 , 0.5 , 0.2 , 0.1 , 0.05 , 0.02 , 0.01.
(6) 精确到1,0.1,0.01,0.001……的不足近似值与过剩近似值分别构成数列:
1,1.4, 1.41, 1.414, ……
2, 1.5, 1.43, 1.415, ……
有限、递减
(5)-1的1次幂,2次幂,3次幂,4次幂:
-1, 1 ,-1 , 1,……
(4)目前通用的人民币面额按从大到小的顺序构成数列(单位:元):100 , 50 , 20 , 10 , 5 , 2 , 1 , 0.5 , 0.2 , 0.1 , 0.05 , 0.02 , 0.01.
(6) 精确到1,0.1,0.01,0.001……的不足近似值与过剩近似值分别构成数列:
1,1.4, 1.41, 1.414, ……
2, 1.5, 1.43, 1.415, ……
有限、递减
无限、摆动
(5)-1的1次幂,2次幂,3次幂,4次幂:
-1, 1 ,-1 , 1,……
(4)目前通用的人民币面额按从大到小的顺序构成数列(单位:元):100 , 50 , 20 , 10 , 5 , 2 , 1 , 0.5 , 0.2 , 0.1 , 0.05 , 0.02 , 0.01.
(6) 精确到1,0.1,0.01,0.001……的不足近似值与过剩近似值分别构成数列:
1,1.4, 1.41, 1.414, ……
2, 1.5, 1.43, 1.415, ……
有限、递减
无限、摆动
无限、递增
(5)-1的1次幂,2次幂,3次幂,4次幂:
-1, 1 ,-1 , 1,……
(4)目前通用的人民币面额按从大到小的顺序构成数列(单位:元):100 , 50 , 20 , 10 , 5 , 2 , 1 , 0.5 , 0.2 , 0.1 , 0.05 , 0.02 , 0.01.
(6) 精确到1,0.1,0.01,0.001……的不足近似值与过剩近似值分别构成数列:
1,1.4, 1.41, 1.414, ……
2, 1.5, 1.43, 1.415, ……
有限、递减
无限、摆动
无限、递增
无限、递减
(5)-1的1次幂,2次幂,3次幂,4次幂:
-1, 1 ,-1 , 1,……
写出下列数列的一个通项公式。
三、例题精析
【例2】
变式. 写出下列数列的一个通项公式。
探究2:若数列{an}的通项公式为an=-2n2+15n+5, 则数列中最大的一项是第____项,值为_________。
探究2:若数列{an}的通项公式为an=-2n2+15n+5, 则数列中最大的一项是第____项,值为_________。
4
33
