2021-2022学年鲁教版(五四制)九年级数学上册3.3二次函数y=ax2的图象与性质同步达标训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学上册3.3二次函数y=ax2的图象与性质同步达标训练(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 269.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学上册《3.3二次函数y=ax2的图象与性质》
同步达标训练(附答案)
1.对于任意实数h,抛物线y=(x﹣h)2与抛物线y=x2( )
A.开口方向相同 B.对称轴相同
C.顶点相同 D.都有最高点
2.抛物线y=﹣2(x﹣3)2的顶点坐标和对称轴分别为( )
A.(﹣3,0),直线x=﹣3 B.(3,0),直线x=3
C.(0,﹣3),直线x=﹣3 D.(0,3),直线x=﹣3
3.对于函数y=﹣2(x﹣1)2的图象,下列说法不正确的是( )
A.开口向下 B.对称轴是直线x=1
C.最大值为0 D.与y轴不相交
4.二次函数y=(x﹣1)2图象的对称轴是( )
A.直线x=﹣1 B.直线x=1 C.直线x=﹣2 D.直线x=2
5.顶点为(﹣3,0),且开口方向、形状与函数y=﹣的图象相同的抛物线是( )
A.y=﹣ B.y=﹣+3 C.y=﹣ D.y=﹣3
6.顶点为(5,0)且开口方向、形状与函数y=﹣x2的图象相同的抛物线是( )
A.y=﹣(x﹣5)2 B.y=﹣x2﹣5
C.y=﹣(x+5)2 D.y=(x+5)2
7.对于二次函数y=3(x+1)2,下列结论正确的是( )
A.当x取任何实数时,y的值总是正的 B.其图象的顶点坐标为(0,1)
C.当x>1时,y随x的增大而增大 D.其图象关于x轴对称
8.已知二次函数y=﹣3(x﹣1)2,下列说法正确的有( )
①因为a=﹣3,所以开口方向向上;②顶点坐标为(1,0);
③对称轴为直线x=1;④当x>0时,y随x的增大而增大.
A.0个 B.1个 C.2个 D.3个
9.对于y=2(x﹣3)2的图象,下列叙述不正确的是( )
A.顶点坐标为(﹣3,0) B.对称轴为直线x=3
C.当x=3时,y有最小值0 D.x>3时,y随x的增大而增大
10.比较抛物线y=x2、y=2x2﹣1、y=0.5(x﹣1)2的共同点,其中说法正确的是( )
A.顶点都是原点 B.对称轴都是y轴
C.开口方向都向上 D.开口大小相同
11.已知二次函数y=3(x﹣a)2的图象上,当x>2时,y随x的增大而增大,则a的取值范围是( )
A.a<2 B.a≥2 C.a≤2 D.a≤﹣2
12.已知二次函数y=﹣(x+h)2,当x<﹣3时,y随x的增大而增大,当x>﹣3时,y随x的增大而减小,当x=0时,y的值为( )
A.﹣1 B.﹣9 C.1 D.9
13.若抛物线y=x2﹣mx+9的顶点在x轴上,则m的值为( )
A.6 B.﹣6 C.±6 D.无法确定
14.抛物线y=﹣3(x﹣1)2的开口方向 ,对称轴是 ,顶点坐标是 .
15.已知二次函数y=﹣(x﹣2)2,当x 时,y随x的增大而减小.
16.若抛物线y=a(x+k)2的对称轴为x=3,且它与抛物线y=﹣2x2的形状相同,开口方向相同,则k= ,a= .
17.抛物线y=x2﹣kx+4的顶点在x轴上,则k的值是 .
18.当x 时,函数y=﹣(x+3)2y随x的增大而增大,当x 时,随x的增大而减小.
19.对于二次函数y=﹣4(x﹣1)2,当x1<0,1<x2<2,则相应的函数值之间的大小关系是y1 y2.
20.已知二次函数y=2(x﹣h)2的图象上,当x>3时,y随x的增大而增大,则h的取值范围是 .
21.如图,抛物线y=x2+2x+1的顶点为M,与y轴交于点C,A是抛物线上的一点,且AM=CM,则△ACM的面积为 .
22.填表:
抛物线 开口方向 对称轴 顶点坐标
y=2(x+3)2
y=﹣3(x﹣3)2
y=﹣4(x﹣3)2
23.在直角坐标系中画出函数y=(x﹣3)2的图象
(1)指出该函数图象的开口方向、顶点坐标和对称轴;
(2)试说明函数与二次函数y=x2的图象的关系;
(3)根据图象说明何时y有最大(小)值,是多少.
24.在同一坐标系中画出二次函数y=2x2,y=2x2+1和y=2(x+1)2的图象,并回答下列问题:
(1)它们的形状相同吗?
(2)分别说出它们的开口方向、顶点坐标和对称轴.
25.已知抛物线y=a(x﹣h)2的对称轴是直线x=﹣1,与y轴交于点(0,2),求a和h的值.
26.有一个二次函数y=a(x﹣k)2的图象,三位同学分别说出了它的一些特点:
甲:开口向上;
乙:对称轴是直线x=2;
丙:与y轴的交点到原点的距离为2.
请你写出满足上述全部特点的二次函数的解析式.
27.二次函数y=(x﹣m)2的图象如图所示.且OA=OC,求该函数的解析式.
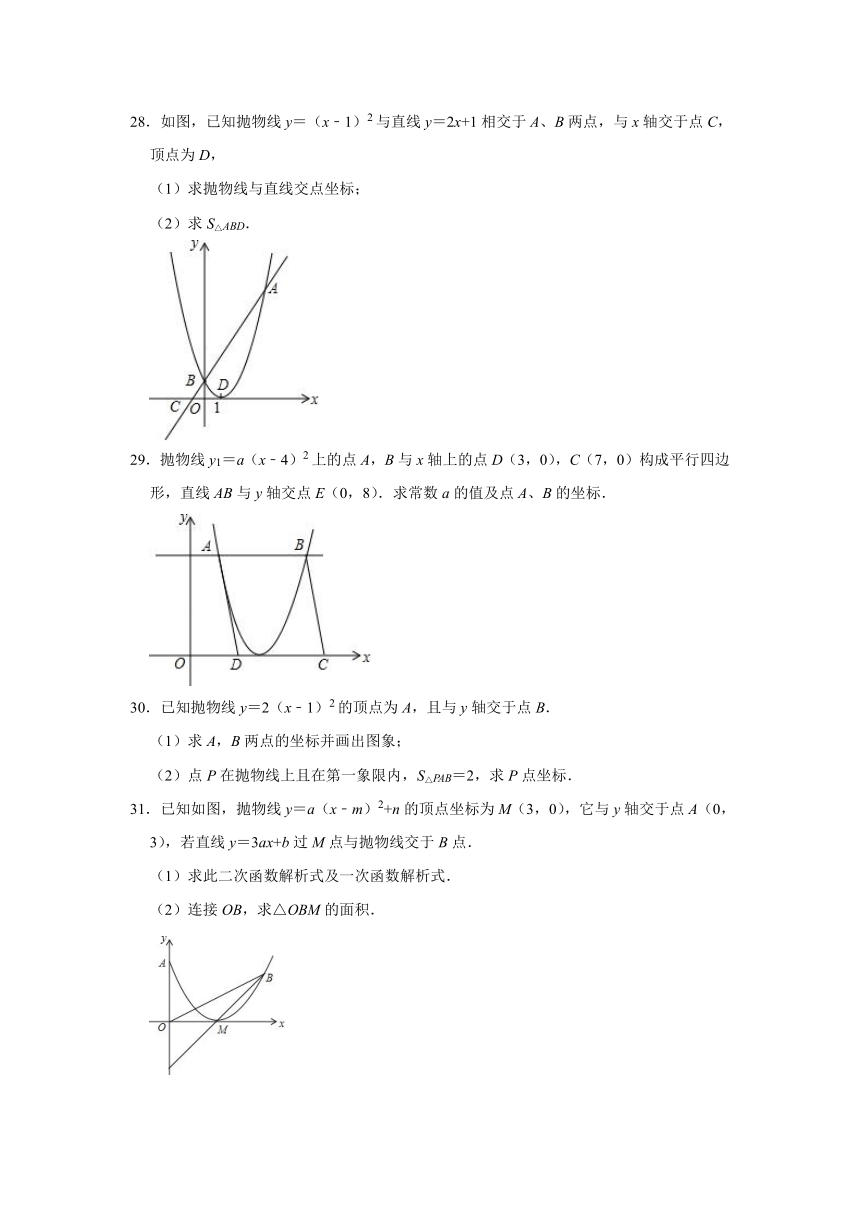
28.如图,已知抛物线y=(x﹣1)2与直线y=2x+1相交于A、B两点,与x轴交于点C,顶点为D,
(1)求抛物线与直线交点坐标;
(2)求S△ABD.
29.抛物线y1=a(x﹣4)2上的点A,B与x轴上的点D(3,0),C(7,0)构成平行四边形,直线AB与y轴交点E(0,8).求常数a的值及点A、B的坐标.
30.已知抛物线y=2(x﹣1)2的顶点为A,且与y轴交于点B.
(1)求A,B两点的坐标并画出图象;
(2)点P在抛物线上且在第一象限内,S△PAB=2,求P点坐标.
31.已知如图,抛物线y=a(x﹣m)2+n的顶点坐标为M(3,0),它与y轴交于点A(0,3),若直线y=3ax+b过M点与抛物线交于B点.
(1)求此二次函数解析式及一次函数解析式.
(2)连接OB,求△OBM的面积.
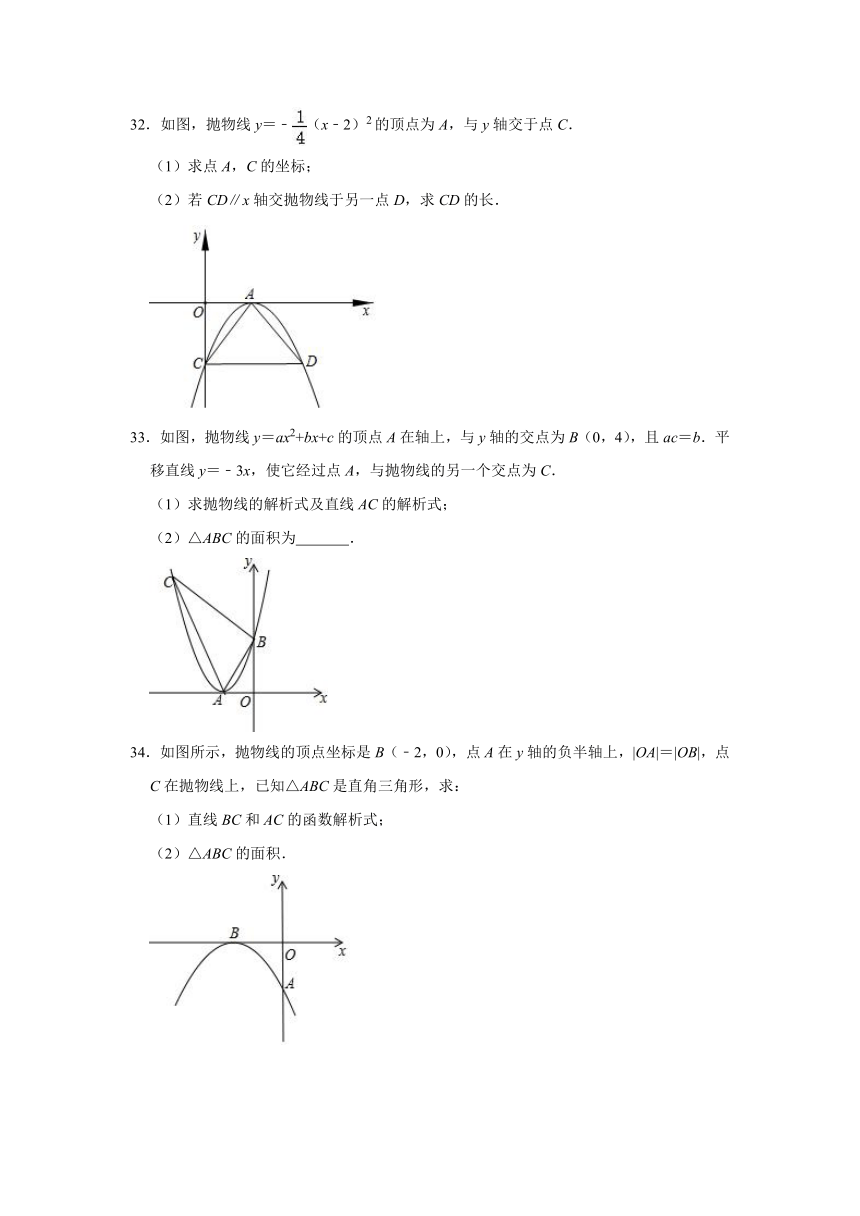
32.如图,抛物线y=﹣(x﹣2)2的顶点为A,与y轴交于点C.
(1)求点A,C的坐标;
(2)若CD∥x轴交抛物线于另一点D,求CD的长.
33.如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=﹣3x,使它经过点A,与抛物线的另一个交点为C.
(1)求抛物线的解析式及直线AC的解析式;
(2)△ABC的面积为 .
34.如图所示,抛物线的顶点坐标是B(﹣2,0),点A在y轴的负半轴上,|OA|=|OB|,点C在抛物线上,已知△ABC是直角三角形,求:
(1)直线BC和AC的函数解析式;
(2)△ABC的面积.
参考答案
1.解:抛物线y=(x﹣h)2与抛物线y=x2,
A、a=1>0,都开口向上,此说法正确;
B、抛物线y=(x﹣h)2对称轴x=h,抛物线y=x2对称轴x=0,说法错误;
C、抛物线y=(x﹣h)2顶点是(h,0),抛物线y=x2顶点是(0,0),说法错误;
D、a>0,都有最低点,说法错误.
故选:A.
2.解:抛物线y=﹣2(x﹣3)2的顶点坐标为(3,0),对称轴为x=3.
故选:B.
3.解:对于函数y=﹣2(x﹣1)2的图象,
∵a=﹣2<0,
∴开口向下,对称轴x=1,顶点坐标为(1,0),函数有最大值0,
故A、B、C正确,
故选:D.
4.解:∵y=(x﹣1)2是抛物线的顶点式,
∴对称轴为直线x=1.
故选:B.
5.解:y=﹣的顶点为(3,0),故选项A不符合题意;
y=﹣+3的顶点为(0,3),故选项B不符合题意;
y=的顶点为(﹣3,0),开口方向、形状与函数y=﹣的图象相同,故选项C符合题意;
y=的顶点为(0,﹣3),故选项D不符合题意;
故选:C.
6.解:设抛物线的解析式为y=a(x﹣h)2+k,且该抛物线的形状与开口方向和抛物线y=﹣x2相同,
∴a=﹣,
∴y=﹣(x﹣h)2+k,
∴y=﹣(x﹣5)2.
故选:A.
7.解:∵二次函数的解析式为y=3(x+1)2,
∴无论x为何值,y≥0;二次函数图象的顶点坐标为(﹣1,0);当x>﹣1时,y随x的增大而增大;二次函数的图象关于直线x=﹣1对称.
故选:C.
8.解:∵y=﹣3(x﹣1)2中,a=﹣3<0,
∴抛物线开口方向向下,对称轴为直线x=1,顶点为(1,0),
∴当x<1时,y随x的增大而增大,
故②③2个,
故选:C.
9.解:∵y=2(x﹣3)2,
∴该函数的顶点坐标为(3,0),故选项A错误;
对称轴是直线x=3,故选项B正确;
当x=3时,y有最小值0,故选项C正确;
当x>3时,y随x的增大而增大,故选项D正确;
故选:A.
10.解:y=x2的顶点坐标为原点,对称轴是y轴,开口向上;
y=2x2﹣1的顶点坐标为(0,﹣1),对称轴是y轴,开口向上;
y=0.5(x﹣1)2的顶点坐标为(1,0),对称轴是直线x=1,开口向上;
综合判断开口方向都向上,
故选:C.
11.解:二次函数y=3(x﹣a)2的对称轴为直线x=a,
∵当x>a时,y的值随x值的增大而增大,
∴a≤2.
故选:C.
12.解:由题意得:二次函数y=﹣(x+h)2的对称轴为x=﹣3,
故h=3,
把h=3代入二次函数y=﹣(x+h)2可得y=﹣(x+3)2,
当x=0时,y=﹣9,
故选:B.
13.解:∵抛物线y=x2﹣mx+9的顶点在x轴上,
∴b2﹣4ac=m2﹣36=0,
∴m=±6,
故选:C.
14.解:由y=﹣3(x﹣1)2可知,二次项系数为﹣3<0,
∴抛物线开口向下,对称轴为直线x=1,
顶点坐标为(1,0).
故本题答案为:向下,x=1,(1,0).
15.解:
∵y=﹣(x﹣2)2,
∴抛物线开口向下,对称轴为x=2,
∴当x>2时,y随x的增大而减小,
故答案为:>2.
16.解:∵抛物线y=a(x+k)2的对称轴是直线x=3,
∴k=﹣3,
∵它与抛物线y=﹣2x2的形状相同,开口方向相同,
∴a=﹣2.
故答案为﹣3,﹣2.
17.解:∵抛物线y=x2﹣kx+4的顶点在x轴上,
∴=0,
∴k=±4.
故答案为:±4.
18.解:∵函数y=﹣(x+3)2的对称轴为x=﹣3,且开口向下,
∴当x<﹣3时,函数y=﹣(x+3)2y随x的增大而增大,当x>﹣3时,随x的增大而减小.
故答案为:<﹣3,>﹣3.
19.解:∵二次函数y=﹣4(x﹣1)2,
∴抛物线开口向下,对称轴为直线x=1,
∵x1<0,1<x2<2,
∴|x1﹣1|>|x2﹣1|,
∴y1<y2,
故答案为<.
20.解:二次函数y=2(x﹣h)2的对称轴为直线x=h,
∵x>3时,y随x的增大而增大,
∴h≤3.
故答案为:h≤3.
21.解:∵y=x2+2x+1=(x+1)2,
∴C(0,1),顶点(﹣1,0),
∵A是抛物线上的一点,且AM=CM,
∴A是C的对称点,
∵AC∥x轴,
∴AC=2,OC=1,
∴S△ACM=×2×1=1,
故答案为1.
22.解:填表如下:
抛物线 开口方向 对称轴 顶点坐标
y=2(x+3)2 开口向上 直线x=﹣3 (﹣3,0)
y=﹣3(x﹣3)2 开口向下 直线x=3 (3,0)
y=﹣4(x﹣3)2 开口向下 直线x=3 (3,0)
23.解:函数y=(x﹣3)2的图象如图所示:
(1)函数图象的开口方向向上、顶点坐标(3,0)和对称轴为x=3;
(2)函数与二次函数y=x2的图象的关系:二次函数y=x2的图象箱左平移三个单位得到函数y=(x﹣3)2的图象;
(3)y有最小值,最小值为0.
24.解:画出函数的图象如图:
(1)它们的形状相同;
(2)函数y=2x2的开口向上,顶点坐标为(0,0),对称轴是y轴;函数y=2x2+1的开口向上,顶点坐标为(0,1),对称轴是y轴;函数y=2(x+1)2的开口向上,顶点坐标为(﹣1,0),对称轴是直线x=﹣1.
25.解:已知抛物线y=a(x﹣h)2的对称轴为直线x=﹣1,
h=﹣1,
抛物线y=a(x+1)2与y轴交于点(0,2),
把(0,2)代入y=a(x+1)2得
a=2,
解得a=2.
26.解:∵二次函数y=a(x﹣k)2的图象开口向上,
∴a>0,
∵对称轴为直线x=2,
∴k=2,
∴二次函数y=a(x﹣k)2的解析式为y=a(x﹣2)2,
∵与y轴的交点到原点的距离为2,
∴与y轴交于点(0,2)或(0,﹣2),
把(0,2)代入得,2=4a,
∴a=,
把(0,﹣2)代入得,﹣2=4a,
∴a=﹣(舍去)
∴解析式为:y=(x﹣2)2.
27.解:∵二次函数y=(x﹣m)2的对称轴为直线x=m,
∴OC=m.
当x=0时,y=(x﹣m)2=m2,
∴OA=m2.
又∵OA=OC,即m=m2,
∴m1=0,m2=2.
观察函数图象,可知:m1=0舍去,
∴该函数的解析式为y=(x﹣2)2,即y=x2﹣2x+2.
28.解:(1)由题意可知:,
解得:,,
A点坐标为(4,9),B点坐标为(0,1);
(2)直线y=2x+1与x轴交于点C,坐标为(﹣,0),顶点D为(1,0),
S△ABD=×1×9﹣××1=.
29.解:如图:,
由四边形ABCD是平行四边形,CD=4,
得AB=CD=4.
由y1=a(x﹣4)2,得
x=4是对称轴,直线AB是y=8,即E(4,8);
AE=BE=AB=2.
4﹣2=2,即A(2,8),
4+2=6,即B(6,8).
将A点坐标代入,得
a(2﹣4)2=8,
解得a=2.
30.解:(1)由y=2(x﹣1)2知顶点A坐标为(1,0),
当x=0时,y=2(x﹣1)2=2,则点B坐标为(0,2),
函数图象如下:
(2)设点P(a,2a2﹣4a+2),
过点P作PC⊥x轴于点C,
则S△PAB=S梯形PBOC﹣S△ABO﹣S△PAC
=×(2+2a2﹣4a+2) a﹣×1×2﹣×(2a2﹣4a+2)×(a﹣1)
=a2﹣a,
∵S△PAB=2,
∴a2﹣a=2,
解得a=﹣1(舍)或a=2,
则点P的坐标为(2,2).
31.解:(1)∵抛物线y=a(x﹣m)2+n的顶点为M(3,0),
∴y=a(x﹣3)2+0.
∵抛物线与y轴交于点A(0,3),
∴3=a(0﹣3)2,
∴a=,
∴抛物线的解析式为:y=(x﹣3)2;
∵y=3ax+b,
∴y=3×x+b,
∴y=x+b.
∵直线经过M(3,0),
∴0=3+b,
∴b=﹣3,
∴直线的解析式为:y=x﹣3.
(2)由题意得
(x﹣3)2=x﹣3
解得:x=3,或x=6
则B点坐标为(6,3),
△OBM的面积=×3×3=.
32.解:(1)∵y=﹣(x﹣2)2,
∴A(2,0),
抛物线y=﹣(x﹣2)2的与y轴的交于点C,
令x=0得y=﹣1.
∴C(0,﹣1);
(2)∵A(2,0),
∴对称轴为直线x=2,
∴C的对称点为(4,﹣1),
∵CD∥x轴交抛物线于另一点D,
∴D(4,﹣1),
∴CD=4﹣0=4.
33.解:(1)∵顶点A在轴上,
∴=0,
∴4ac=b2
∵ac=b.
∴4b=b2,
∵b≠0,
∴b=4,
∵抛物线y=ax2+bx+c与y轴的交点为B(0,4),
∴c=4,
∴a=1,
∴抛物线的解析式为y=x2+4x+4,;
∵y=x2+4x+4=(x+2)2,
∴A(﹣2,0),
∵平移直线y=﹣3x,使它经过点A,与抛物线的另一个交点为C.
∴设直线AC为y=﹣3x+n,
把(﹣2,0)代入得,6+n=0,
∴n=﹣6,
∴直线AC的解析式为y=﹣3x﹣6;
(2)解得或,
∴C(﹣5,9),
把y=4代入y=﹣3x﹣6得x=﹣,
∴S△ABC=××(9﹣4)+××4=15.
故答案为15.
34.解:∵抛物线的顶点坐标是B(﹣2,0),点A在y轴的负半轴上,|OA|=|OB|,
∴A(0,﹣2),
设抛物线的解析式为y=a(x+2)2,
∴﹣2=4a,
解得a=﹣.
∴抛物线的解析式为y=﹣(x+2)2,
易知直线AB的解析式为y=﹣x﹣2,
①当∠ABC=90°时,∵OA=OB,
∴∠OBA=45°,易证△ABC是等腰直角三角形,
∴A、C关于抛物线的对称轴直线x=﹣2对称,
∴C(﹣4,﹣2),
∴直线BC的解析式为y=x+2,直线AC的解析式为y=﹣2,
∴S△ABC=×4×2=4
②当∠CAB=90°时,∵AC⊥AB,
∴直线AC的解析式为y=x﹣2,
由解得或,
∴C′(﹣6,﹣8),
∴直线BC的解析式为y=2x+4,直线AC的解析式为y=x﹣2,
∴S△ABC=×2×6=12.
③∠ACB不可能为90°,此种情形不存在
同步达标训练(附答案)
1.对于任意实数h,抛物线y=(x﹣h)2与抛物线y=x2( )
A.开口方向相同 B.对称轴相同
C.顶点相同 D.都有最高点
2.抛物线y=﹣2(x﹣3)2的顶点坐标和对称轴分别为( )
A.(﹣3,0),直线x=﹣3 B.(3,0),直线x=3
C.(0,﹣3),直线x=﹣3 D.(0,3),直线x=﹣3
3.对于函数y=﹣2(x﹣1)2的图象,下列说法不正确的是( )
A.开口向下 B.对称轴是直线x=1
C.最大值为0 D.与y轴不相交
4.二次函数y=(x﹣1)2图象的对称轴是( )
A.直线x=﹣1 B.直线x=1 C.直线x=﹣2 D.直线x=2
5.顶点为(﹣3,0),且开口方向、形状与函数y=﹣的图象相同的抛物线是( )
A.y=﹣ B.y=﹣+3 C.y=﹣ D.y=﹣3
6.顶点为(5,0)且开口方向、形状与函数y=﹣x2的图象相同的抛物线是( )
A.y=﹣(x﹣5)2 B.y=﹣x2﹣5
C.y=﹣(x+5)2 D.y=(x+5)2
7.对于二次函数y=3(x+1)2,下列结论正确的是( )
A.当x取任何实数时,y的值总是正的 B.其图象的顶点坐标为(0,1)
C.当x>1时,y随x的增大而增大 D.其图象关于x轴对称
8.已知二次函数y=﹣3(x﹣1)2,下列说法正确的有( )
①因为a=﹣3,所以开口方向向上;②顶点坐标为(1,0);
③对称轴为直线x=1;④当x>0时,y随x的增大而增大.
A.0个 B.1个 C.2个 D.3个
9.对于y=2(x﹣3)2的图象,下列叙述不正确的是( )
A.顶点坐标为(﹣3,0) B.对称轴为直线x=3
C.当x=3时,y有最小值0 D.x>3时,y随x的增大而增大
10.比较抛物线y=x2、y=2x2﹣1、y=0.5(x﹣1)2的共同点,其中说法正确的是( )
A.顶点都是原点 B.对称轴都是y轴
C.开口方向都向上 D.开口大小相同
11.已知二次函数y=3(x﹣a)2的图象上,当x>2时,y随x的增大而增大,则a的取值范围是( )
A.a<2 B.a≥2 C.a≤2 D.a≤﹣2
12.已知二次函数y=﹣(x+h)2,当x<﹣3时,y随x的增大而增大,当x>﹣3时,y随x的增大而减小,当x=0时,y的值为( )
A.﹣1 B.﹣9 C.1 D.9
13.若抛物线y=x2﹣mx+9的顶点在x轴上,则m的值为( )
A.6 B.﹣6 C.±6 D.无法确定
14.抛物线y=﹣3(x﹣1)2的开口方向 ,对称轴是 ,顶点坐标是 .
15.已知二次函数y=﹣(x﹣2)2,当x 时,y随x的增大而减小.
16.若抛物线y=a(x+k)2的对称轴为x=3,且它与抛物线y=﹣2x2的形状相同,开口方向相同,则k= ,a= .
17.抛物线y=x2﹣kx+4的顶点在x轴上,则k的值是 .
18.当x 时,函数y=﹣(x+3)2y随x的增大而增大,当x 时,随x的增大而减小.
19.对于二次函数y=﹣4(x﹣1)2,当x1<0,1<x2<2,则相应的函数值之间的大小关系是y1 y2.
20.已知二次函数y=2(x﹣h)2的图象上,当x>3时,y随x的增大而增大,则h的取值范围是 .
21.如图,抛物线y=x2+2x+1的顶点为M,与y轴交于点C,A是抛物线上的一点,且AM=CM,则△ACM的面积为 .
22.填表:
抛物线 开口方向 对称轴 顶点坐标
y=2(x+3)2
y=﹣3(x﹣3)2
y=﹣4(x﹣3)2
23.在直角坐标系中画出函数y=(x﹣3)2的图象
(1)指出该函数图象的开口方向、顶点坐标和对称轴;
(2)试说明函数与二次函数y=x2的图象的关系;
(3)根据图象说明何时y有最大(小)值,是多少.
24.在同一坐标系中画出二次函数y=2x2,y=2x2+1和y=2(x+1)2的图象,并回答下列问题:
(1)它们的形状相同吗?
(2)分别说出它们的开口方向、顶点坐标和对称轴.
25.已知抛物线y=a(x﹣h)2的对称轴是直线x=﹣1,与y轴交于点(0,2),求a和h的值.
26.有一个二次函数y=a(x﹣k)2的图象,三位同学分别说出了它的一些特点:
甲:开口向上;
乙:对称轴是直线x=2;
丙:与y轴的交点到原点的距离为2.
请你写出满足上述全部特点的二次函数的解析式.
27.二次函数y=(x﹣m)2的图象如图所示.且OA=OC,求该函数的解析式.
28.如图,已知抛物线y=(x﹣1)2与直线y=2x+1相交于A、B两点,与x轴交于点C,顶点为D,
(1)求抛物线与直线交点坐标;
(2)求S△ABD.
29.抛物线y1=a(x﹣4)2上的点A,B与x轴上的点D(3,0),C(7,0)构成平行四边形,直线AB与y轴交点E(0,8).求常数a的值及点A、B的坐标.
30.已知抛物线y=2(x﹣1)2的顶点为A,且与y轴交于点B.
(1)求A,B两点的坐标并画出图象;
(2)点P在抛物线上且在第一象限内,S△PAB=2,求P点坐标.
31.已知如图,抛物线y=a(x﹣m)2+n的顶点坐标为M(3,0),它与y轴交于点A(0,3),若直线y=3ax+b过M点与抛物线交于B点.
(1)求此二次函数解析式及一次函数解析式.
(2)连接OB,求△OBM的面积.
32.如图,抛物线y=﹣(x﹣2)2的顶点为A,与y轴交于点C.
(1)求点A,C的坐标;
(2)若CD∥x轴交抛物线于另一点D,求CD的长.
33.如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=﹣3x,使它经过点A,与抛物线的另一个交点为C.
(1)求抛物线的解析式及直线AC的解析式;
(2)△ABC的面积为 .
34.如图所示,抛物线的顶点坐标是B(﹣2,0),点A在y轴的负半轴上,|OA|=|OB|,点C在抛物线上,已知△ABC是直角三角形,求:
(1)直线BC和AC的函数解析式;
(2)△ABC的面积.
参考答案
1.解:抛物线y=(x﹣h)2与抛物线y=x2,
A、a=1>0,都开口向上,此说法正确;
B、抛物线y=(x﹣h)2对称轴x=h,抛物线y=x2对称轴x=0,说法错误;
C、抛物线y=(x﹣h)2顶点是(h,0),抛物线y=x2顶点是(0,0),说法错误;
D、a>0,都有最低点,说法错误.
故选:A.
2.解:抛物线y=﹣2(x﹣3)2的顶点坐标为(3,0),对称轴为x=3.
故选:B.
3.解:对于函数y=﹣2(x﹣1)2的图象,
∵a=﹣2<0,
∴开口向下,对称轴x=1,顶点坐标为(1,0),函数有最大值0,
故A、B、C正确,
故选:D.
4.解:∵y=(x﹣1)2是抛物线的顶点式,
∴对称轴为直线x=1.
故选:B.
5.解:y=﹣的顶点为(3,0),故选项A不符合题意;
y=﹣+3的顶点为(0,3),故选项B不符合题意;
y=的顶点为(﹣3,0),开口方向、形状与函数y=﹣的图象相同,故选项C符合题意;
y=的顶点为(0,﹣3),故选项D不符合题意;
故选:C.
6.解:设抛物线的解析式为y=a(x﹣h)2+k,且该抛物线的形状与开口方向和抛物线y=﹣x2相同,
∴a=﹣,
∴y=﹣(x﹣h)2+k,
∴y=﹣(x﹣5)2.
故选:A.
7.解:∵二次函数的解析式为y=3(x+1)2,
∴无论x为何值,y≥0;二次函数图象的顶点坐标为(﹣1,0);当x>﹣1时,y随x的增大而增大;二次函数的图象关于直线x=﹣1对称.
故选:C.
8.解:∵y=﹣3(x﹣1)2中,a=﹣3<0,
∴抛物线开口方向向下,对称轴为直线x=1,顶点为(1,0),
∴当x<1时,y随x的增大而增大,
故②③2个,
故选:C.
9.解:∵y=2(x﹣3)2,
∴该函数的顶点坐标为(3,0),故选项A错误;
对称轴是直线x=3,故选项B正确;
当x=3时,y有最小值0,故选项C正确;
当x>3时,y随x的增大而增大,故选项D正确;
故选:A.
10.解:y=x2的顶点坐标为原点,对称轴是y轴,开口向上;
y=2x2﹣1的顶点坐标为(0,﹣1),对称轴是y轴,开口向上;
y=0.5(x﹣1)2的顶点坐标为(1,0),对称轴是直线x=1,开口向上;
综合判断开口方向都向上,
故选:C.
11.解:二次函数y=3(x﹣a)2的对称轴为直线x=a,
∵当x>a时,y的值随x值的增大而增大,
∴a≤2.
故选:C.
12.解:由题意得:二次函数y=﹣(x+h)2的对称轴为x=﹣3,
故h=3,
把h=3代入二次函数y=﹣(x+h)2可得y=﹣(x+3)2,
当x=0时,y=﹣9,
故选:B.
13.解:∵抛物线y=x2﹣mx+9的顶点在x轴上,
∴b2﹣4ac=m2﹣36=0,
∴m=±6,
故选:C.
14.解:由y=﹣3(x﹣1)2可知,二次项系数为﹣3<0,
∴抛物线开口向下,对称轴为直线x=1,
顶点坐标为(1,0).
故本题答案为:向下,x=1,(1,0).
15.解:
∵y=﹣(x﹣2)2,
∴抛物线开口向下,对称轴为x=2,
∴当x>2时,y随x的增大而减小,
故答案为:>2.
16.解:∵抛物线y=a(x+k)2的对称轴是直线x=3,
∴k=﹣3,
∵它与抛物线y=﹣2x2的形状相同,开口方向相同,
∴a=﹣2.
故答案为﹣3,﹣2.
17.解:∵抛物线y=x2﹣kx+4的顶点在x轴上,
∴=0,
∴k=±4.
故答案为:±4.
18.解:∵函数y=﹣(x+3)2的对称轴为x=﹣3,且开口向下,
∴当x<﹣3时,函数y=﹣(x+3)2y随x的增大而增大,当x>﹣3时,随x的增大而减小.
故答案为:<﹣3,>﹣3.
19.解:∵二次函数y=﹣4(x﹣1)2,
∴抛物线开口向下,对称轴为直线x=1,
∵x1<0,1<x2<2,
∴|x1﹣1|>|x2﹣1|,
∴y1<y2,
故答案为<.
20.解:二次函数y=2(x﹣h)2的对称轴为直线x=h,
∵x>3时,y随x的增大而增大,
∴h≤3.
故答案为:h≤3.
21.解:∵y=x2+2x+1=(x+1)2,
∴C(0,1),顶点(﹣1,0),
∵A是抛物线上的一点,且AM=CM,
∴A是C的对称点,
∵AC∥x轴,
∴AC=2,OC=1,
∴S△ACM=×2×1=1,
故答案为1.
22.解:填表如下:
抛物线 开口方向 对称轴 顶点坐标
y=2(x+3)2 开口向上 直线x=﹣3 (﹣3,0)
y=﹣3(x﹣3)2 开口向下 直线x=3 (3,0)
y=﹣4(x﹣3)2 开口向下 直线x=3 (3,0)
23.解:函数y=(x﹣3)2的图象如图所示:
(1)函数图象的开口方向向上、顶点坐标(3,0)和对称轴为x=3;
(2)函数与二次函数y=x2的图象的关系:二次函数y=x2的图象箱左平移三个单位得到函数y=(x﹣3)2的图象;
(3)y有最小值,最小值为0.
24.解:画出函数的图象如图:
(1)它们的形状相同;
(2)函数y=2x2的开口向上,顶点坐标为(0,0),对称轴是y轴;函数y=2x2+1的开口向上,顶点坐标为(0,1),对称轴是y轴;函数y=2(x+1)2的开口向上,顶点坐标为(﹣1,0),对称轴是直线x=﹣1.
25.解:已知抛物线y=a(x﹣h)2的对称轴为直线x=﹣1,
h=﹣1,
抛物线y=a(x+1)2与y轴交于点(0,2),
把(0,2)代入y=a(x+1)2得
a=2,
解得a=2.
26.解:∵二次函数y=a(x﹣k)2的图象开口向上,
∴a>0,
∵对称轴为直线x=2,
∴k=2,
∴二次函数y=a(x﹣k)2的解析式为y=a(x﹣2)2,
∵与y轴的交点到原点的距离为2,
∴与y轴交于点(0,2)或(0,﹣2),
把(0,2)代入得,2=4a,
∴a=,
把(0,﹣2)代入得,﹣2=4a,
∴a=﹣(舍去)
∴解析式为:y=(x﹣2)2.
27.解:∵二次函数y=(x﹣m)2的对称轴为直线x=m,
∴OC=m.
当x=0时,y=(x﹣m)2=m2,
∴OA=m2.
又∵OA=OC,即m=m2,
∴m1=0,m2=2.
观察函数图象,可知:m1=0舍去,
∴该函数的解析式为y=(x﹣2)2,即y=x2﹣2x+2.
28.解:(1)由题意可知:,
解得:,,
A点坐标为(4,9),B点坐标为(0,1);
(2)直线y=2x+1与x轴交于点C,坐标为(﹣,0),顶点D为(1,0),
S△ABD=×1×9﹣××1=.
29.解:如图:,
由四边形ABCD是平行四边形,CD=4,
得AB=CD=4.
由y1=a(x﹣4)2,得
x=4是对称轴,直线AB是y=8,即E(4,8);
AE=BE=AB=2.
4﹣2=2,即A(2,8),
4+2=6,即B(6,8).
将A点坐标代入,得
a(2﹣4)2=8,
解得a=2.
30.解:(1)由y=2(x﹣1)2知顶点A坐标为(1,0),
当x=0时,y=2(x﹣1)2=2,则点B坐标为(0,2),
函数图象如下:
(2)设点P(a,2a2﹣4a+2),
过点P作PC⊥x轴于点C,
则S△PAB=S梯形PBOC﹣S△ABO﹣S△PAC
=×(2+2a2﹣4a+2) a﹣×1×2﹣×(2a2﹣4a+2)×(a﹣1)
=a2﹣a,
∵S△PAB=2,
∴a2﹣a=2,
解得a=﹣1(舍)或a=2,
则点P的坐标为(2,2).
31.解:(1)∵抛物线y=a(x﹣m)2+n的顶点为M(3,0),
∴y=a(x﹣3)2+0.
∵抛物线与y轴交于点A(0,3),
∴3=a(0﹣3)2,
∴a=,
∴抛物线的解析式为:y=(x﹣3)2;
∵y=3ax+b,
∴y=3×x+b,
∴y=x+b.
∵直线经过M(3,0),
∴0=3+b,
∴b=﹣3,
∴直线的解析式为:y=x﹣3.
(2)由题意得
(x﹣3)2=x﹣3
解得:x=3,或x=6
则B点坐标为(6,3),
△OBM的面积=×3×3=.
32.解:(1)∵y=﹣(x﹣2)2,
∴A(2,0),
抛物线y=﹣(x﹣2)2的与y轴的交于点C,
令x=0得y=﹣1.
∴C(0,﹣1);
(2)∵A(2,0),
∴对称轴为直线x=2,
∴C的对称点为(4,﹣1),
∵CD∥x轴交抛物线于另一点D,
∴D(4,﹣1),
∴CD=4﹣0=4.
33.解:(1)∵顶点A在轴上,
∴=0,
∴4ac=b2
∵ac=b.
∴4b=b2,
∵b≠0,
∴b=4,
∵抛物线y=ax2+bx+c与y轴的交点为B(0,4),
∴c=4,
∴a=1,
∴抛物线的解析式为y=x2+4x+4,;
∵y=x2+4x+4=(x+2)2,
∴A(﹣2,0),
∵平移直线y=﹣3x,使它经过点A,与抛物线的另一个交点为C.
∴设直线AC为y=﹣3x+n,
把(﹣2,0)代入得,6+n=0,
∴n=﹣6,
∴直线AC的解析式为y=﹣3x﹣6;
(2)解得或,
∴C(﹣5,9),
把y=4代入y=﹣3x﹣6得x=﹣,
∴S△ABC=××(9﹣4)+××4=15.
故答案为15.
34.解:∵抛物线的顶点坐标是B(﹣2,0),点A在y轴的负半轴上,|OA|=|OB|,
∴A(0,﹣2),
设抛物线的解析式为y=a(x+2)2,
∴﹣2=4a,
解得a=﹣.
∴抛物线的解析式为y=﹣(x+2)2,
易知直线AB的解析式为y=﹣x﹣2,
①当∠ABC=90°时,∵OA=OB,
∴∠OBA=45°,易证△ABC是等腰直角三角形,
∴A、C关于抛物线的对称轴直线x=﹣2对称,
∴C(﹣4,﹣2),
∴直线BC的解析式为y=x+2,直线AC的解析式为y=﹣2,
∴S△ABC=×4×2=4
②当∠CAB=90°时,∵AC⊥AB,
∴直线AC的解析式为y=x﹣2,
由解得或,
∴C′(﹣6,﹣8),
∴直线BC的解析式为y=2x+4,直线AC的解析式为y=x﹣2,
∴S△ABC=×2×6=12.
③∠ACB不可能为90°,此种情形不存在
