2021-2022学年鲁教版(五四制)九年级数学上册3.4二次函数y=ax2+bx+c的图象与性质解答题专题训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学上册3.4二次函数y=ax2+bx+c的图象与性质解答题专题训练(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 408.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 21:45:17 | ||
图片预览


文档简介
2021-2022学年鲁教版九年级数学上册《3.4二次函数y=ax2+bx+c的图象与性质》
解答题专题训练(附答案)
1.已知抛物线y=ax2+3经过点A(﹣2,﹣13).
(1)求a的值.
(2)若点P(m,﹣22)在此抛物线上,求点P的坐标.
2.已知抛物线y=ax2经过点A(﹣2,﹣8).
(1)求a的值;
(2)若点P(m,﹣6)在此抛物线上,求点P的坐标.
3.抛物线y=a(x﹣2)2经过点(1,﹣1)
(1)确定a的值;
(2)求出该抛物线与坐标轴的交点坐标.
4.如图,平面直角坐标系中,抛物线y=﹣x2+4x+m﹣4(m为常数)与y轴的交点为C,M(3,0)与N(0,﹣2)分别是x轴、y轴上的点
(1)当m=1时,求抛物线顶点坐标.
(2)若3≤x≤3+m时,函数y=﹣x2+4x+m﹣4有最小值﹣7,求m的值.
(3)若抛物线与线段MN有公共点,直接写出m的取值范围是 .
5.如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,…An…将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;
②抛物线依次经过点A1,A2,A3…An,…
(1)分别写出顶点M1,M2,M3的坐标;
(2)顶点M2019的坐标为( , )
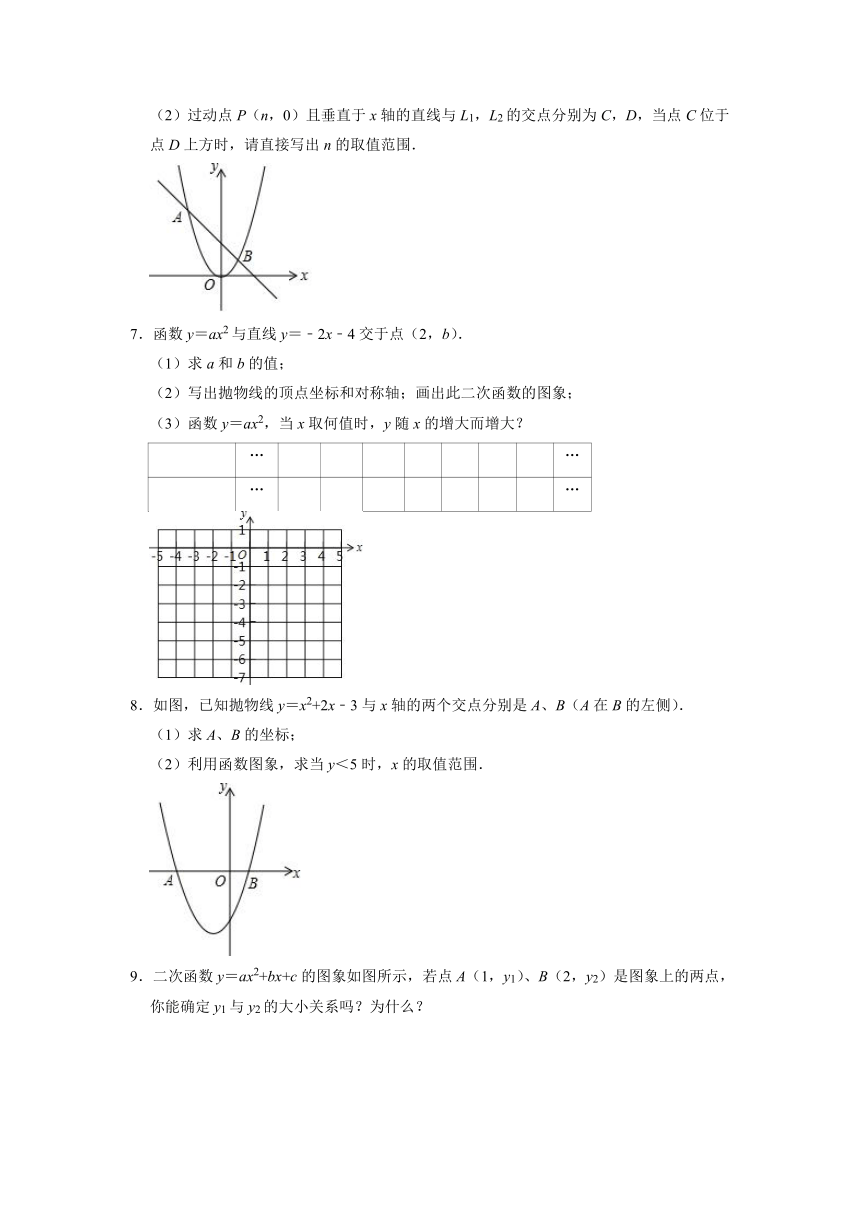
6.如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B(1,1).
(1)求m的值;
(2)过动点P(n,0)且垂直于x轴的直线与L1,L2的交点分别为C,D,当点C位于点D上方时,请直接写出n的取值范围.?
7.函数y=ax2与直线y=﹣2x﹣4交于点(2,b).
(1)求a和b的值;
(2)写出抛物线的顶点坐标和对称轴;画出此二次函数的图象;
(3)函数y=ax2,当x取何值时,y随x的增大而增大?
… …
… …
8.如图,已知抛物线y=x2+2x﹣3与x轴的两个交点分别是A、B(A在B的左侧).
(1)求A、B的坐标;
(2)利用函数图象,求当y<5时,x的取值范围.
9.二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1)、B(2,y2)是图象上的两点,你能确定y1与y2的大小关系吗?为什么?
10.若二次函数y=﹣x2图象平移后得到二次函数y=﹣(x﹣2)2+4的图象.
(1)平移的规律是:先向 (填“左”或“右”)平移 个单位,再向 平移 个单位.
(2)在所给的坐标系内画出二次函数y=﹣(x﹣2)2+4的示意图.
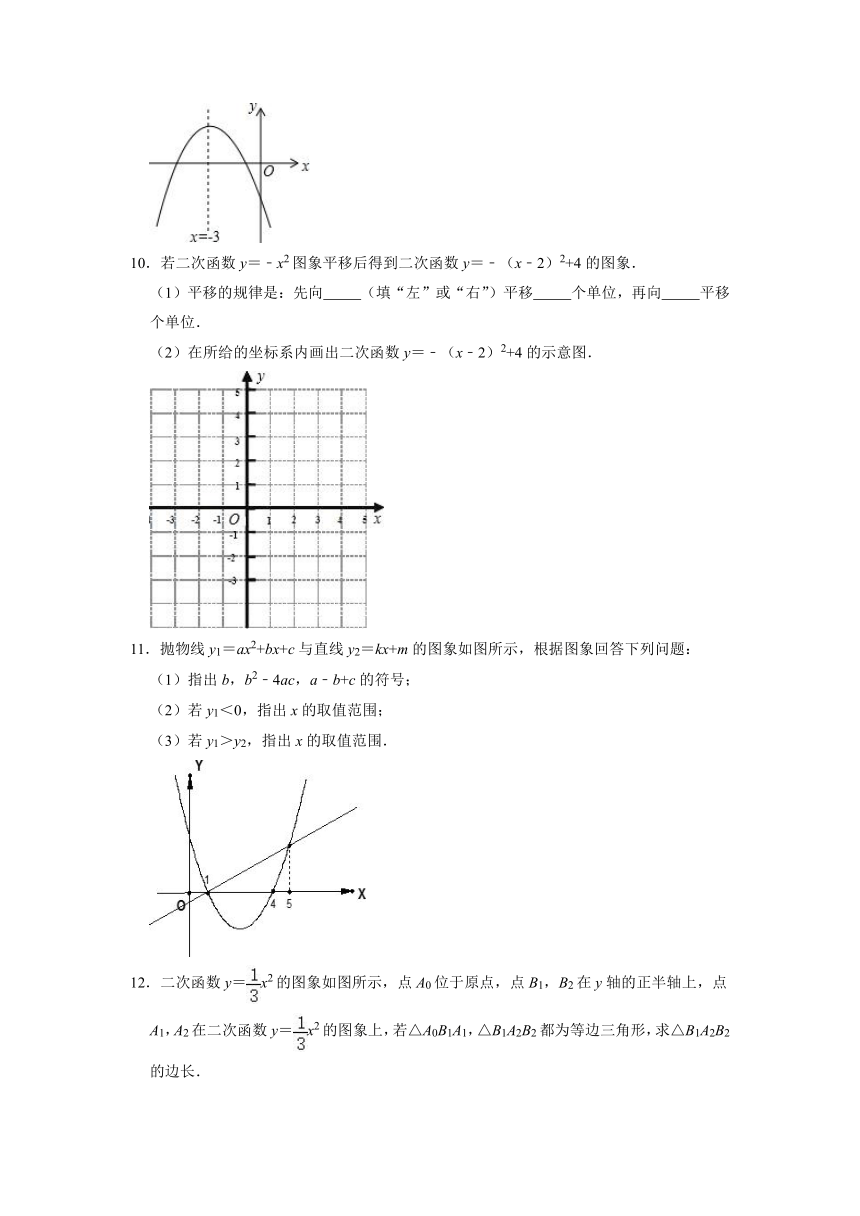
11.抛物线y1=ax2+bx+c与直线y2=kx+m的图象如图所示,根据图象回答下列问题:
(1)指出b,b2﹣4ac,a﹣b+c的符号;
(2)若y1<0,指出x的取值范围;
(3)若y1>y2,指出x的取值范围.
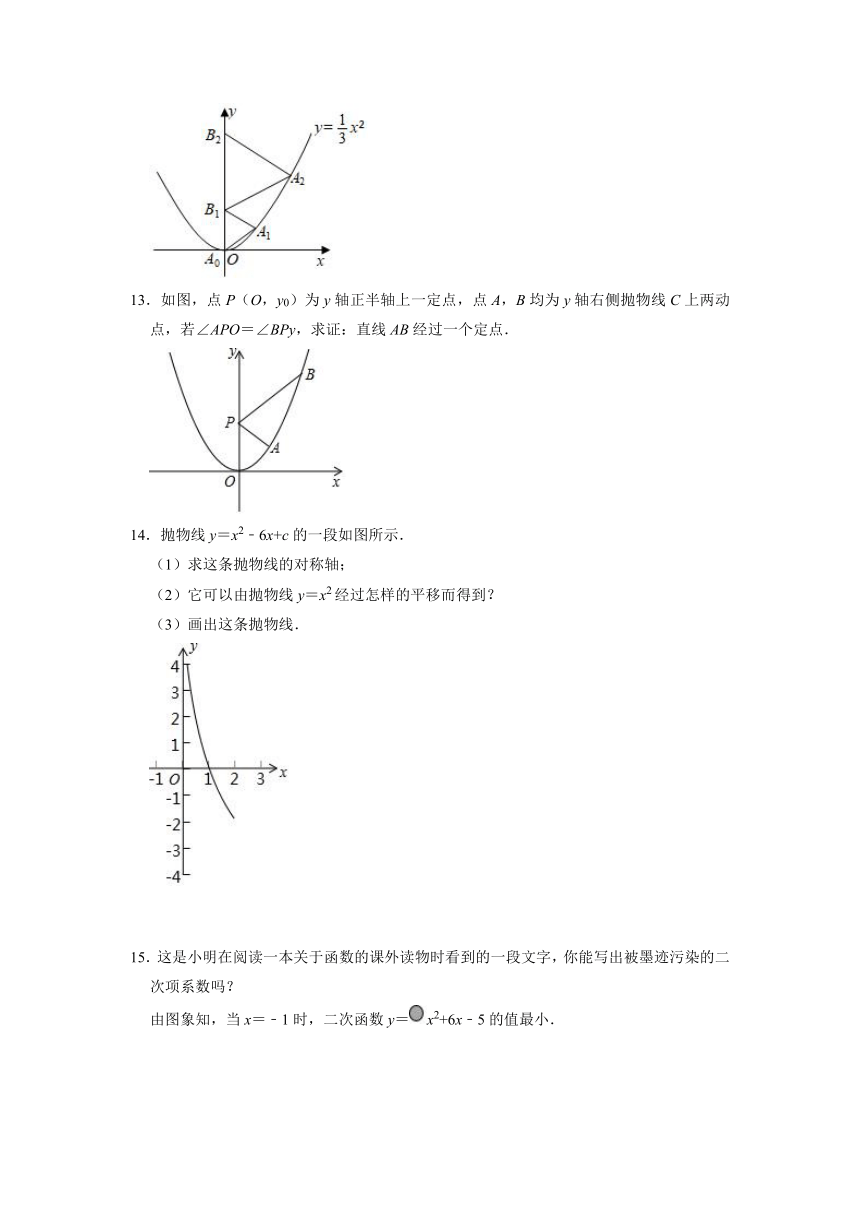
12.二次函数y=x2的图象如图所示,点A0位于原点,点B1,B2在y轴的正半轴上,点A1,A2在二次函数y=x2的图象上,若△A0B1A1,△B1A2B2都为等边三角形,求△B1A2B2的边长.
13.如图,点P(O,y0)为y轴正半轴上一定点,点A,B均为y轴右侧抛物线C上两动点,若∠APO=∠BPy,求证:直线AB经过一个定点.
14.抛物线y=x2﹣6x+c的一段如图所示.
(1)求这条抛物线的对称轴;
(2)它可以由抛物线y=x2经过怎样的平移而得到?
(3)画出这条抛物线.
15.这是小明在阅读一本关于函数的课外读物时看到的一段文字,你能写出被墨迹污染的二次项系数吗?
由图象知,当x=﹣1时,二次函数y=x2+6x﹣5的值最小.
16.抛物线y=x2﹣经过P(1,﹣3),B(4,0)两点,若D是抛物线上的一点,满足∠DPO=∠POB,求点D的坐标.
17.在同一坐标系中画出函数y=x2,y=(x+3)2,y=(x﹣3)2﹣1的图象,并回答:
(1)写出这三个函数的两条相同的特征;
(2)函数y=(x+3)2的图象可由抛物线y=x2怎样平移得到?
(3)函数y=x2的图象可由抛物线y=(x﹣3)2﹣1怎样平移得到?
(4)函数y=(x+3)2﹣1的图象可由抛物线y=(x﹣3)2怎样平移得到?
18.如图,动直线y=kx+2(k>0)与y轴交于点F,与抛物线y=相交于A,B两点,过点A,B分别作x轴的垂线,垂足分别为点C,D,连接CF,DF,请你判断△CDF的形状,并说明理由.
19.已知二次函数y=﹣x2+bx+c经过点(1,5),(3,1).
(1)求b,c的值;
(2)在所给平面直角坐标系中画出该函数的图象(要求列表、描述、连线)
20.如图,过A(1,0)作x轴的垂线,交抛物线y=﹣x2+x于点C.D(3,a)为抛物线上一点,点M为线段OD上的一个动点,MN∥AC交抛物线于点N.
(1)求直线OD的解析式;
(2)若四边形ACNM为平行四边形,求点M的坐标.
参考答案
1.解:(1)将点A(﹣2,﹣13).代入y=ax2+3,得﹣13=4a+3,
解得a=﹣4,
∴抛物线的函数解析式为y=﹣4x2+3,
(2)∵点P(m,﹣22)在此抛物线上,
∴﹣22=﹣4m2+3,
解得m=±,
∴点P的坐标为(,﹣22)或(﹣,﹣22).
2.解:(1)把点A(﹣2,﹣8)代入y=ax2,
得4a=﹣8,
∴a=﹣2;
(2)把点P(m,﹣6)代入y=﹣2x2中,
得﹣2m2=﹣6,
∴m=±,
∴P(,﹣6).
3.解:(1)把(1,﹣1)代入y=a(x﹣2)2得a (1﹣2)2=﹣1
解得a=﹣1
(2)抛物线解析式为y=﹣(x﹣2)2,
当y=0时,﹣(x﹣2)2=0,解得x=2,
所以抛物线与x轴交点坐标为(2,0);
当x=0时,y=﹣(x﹣2)2=﹣4,
所以抛物线与y轴交点坐标为(0,﹣4).
4.解:(1)当m=1时,y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴顶点坐标为(2,1);
(2)由抛物线y=﹣x2+4x+m﹣4(m为常数)可知:开口向上,函数的对称轴为直线x=2,
∴当3≤x≤3+m时,y随x的增大而减小,
∴当x=m+3时,y有最小值﹣7,
∴﹣(m+3)2+4(m+3)+m﹣4=﹣7,
解得m1=2,m2=﹣3(舍去),
∴m=2;
(3)∵M(3,0),N(0,﹣2),
∴直线MN的解析式为y=x﹣2,
∵抛物线与线段MN有公共点,则方程﹣x2+4x+m﹣4=x﹣2,即x2﹣x﹣m+2=0中△≥0,且m﹣4≤﹣2,
∴(﹣)2﹣4(﹣m+2)≥0,
解得﹣≤m≤2,
故答案为﹣≤m≤2.
5.解:(1)∵抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,…,An,…,
∴点An的坐标为(n,n2).
设点Mn的坐标为(a,a),则以点Mn为顶点的抛物线解析式为y=(x﹣a)2+a,
∵点An(n,n2)在抛物线y=(x﹣a)2+a上,
∴n2=(n﹣a)2+a,解得:a=2n﹣1或a=0(舍去),
∴Mn的坐标为(2n﹣1,2n﹣1),
∴顶点M1的坐标为(1,1),顶点M2的坐标为(3,3),顶点M3的坐标为(5,5);
(2)∵Mn的坐标为(2n﹣1,2n﹣1),
∴点M2019,两坐标为:2019×2﹣1=4037,
∴M2019(4037,4037),
故答案为:4037,4037.
6.解:(1)把B(1,1)代入y=ax2得:a=1,
∴抛物线解析式为y=x2.
把A(m,4)代入y=x2得:4=m2,
∴m=±2.
∵点A在二象限,
∴m=﹣2.
(2)观察函数图象可知:当﹣2<x<1时,直线在抛物线的上方,
∴n的取值范围为:﹣2<n<1.
7.解:(1)把(2,b)代入y=﹣2x﹣4得b=﹣4﹣4=﹣8,
把(2,﹣8)代入y=ax2得4a=﹣8,解得a=﹣2;
(2)抛物线y=﹣2x2的顶点坐标为(0,0),对称轴为y轴,
列表:
x … ﹣1.5 ﹣1 ﹣0.5 0 0.5 1 1.5 …
y … ﹣4.5 ﹣2 ﹣0.5 0 ﹣0.5 ﹣2 ﹣4.5 …
描点,连线,如图:
(3)当x<0时,y随x的增大而增大.
8.解:(1)当x2+2x﹣3=0时,解得x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0);
(2)当y=5时,x2+2x﹣3=5,
整理得x2+2x﹣8=0,
解得x1=﹣4,x2=2,
由函数图象可得,当﹣4<x<2时,y<5.
9.解:能定y1与y2的大小关系.
因为抛物线的开口向下,对称轴为直线x=﹣3,
所以当x>﹣3时,y随x的增大而减小,
因为1<2,
所以y1>y2.
10.解:(1)原抛物线的顶点坐标为(0,0),新抛物线的顶点坐标为(2,4),说明新抛物线向右移动了2个单位,向上移动了4个单位.
(2)抓住顶点(2,4),与y轴(0,0),x轴的交点(4,0)(0,0)等关键点来画.
11.解:(1)∵二次函数开口向上a>0,﹣>0,得出b<0,
∴b<0,
∵二次函数与坐标轴的交点个数为2,
∴b2﹣4ac>0,
∵x=﹣1时,y=a﹣b+c,结合图象可知,
∴a﹣b+c>0;
(2)结合图象可知,
当1<x<4 时,y1<0;
(3)结合图象可知,
当x<1 或 x>5时,y1>y2.
12.解:设△A0B1A1的边长为a,△B1B2A2的边长为b,则点A1的坐标为(a,a),点A2的坐标为(b,a+b).
∵点A1、A2在二次函数y=x2的图象上,
∴,
解得:或(不合题意,舍去),
∴△B1A2B2的边长为4.
13.证明:设抛物线的表达式为y=ax2①,
作点A关于y轴的对称轴M,
∵抛物线关于y轴对称,故点M在抛物线上,连接MP,
∵∠MPO=∠OPA=∠BPy,故M、P、B三点共线,
设点A(p,ap2),则点M(﹣p,ap2),
设直线PM的表达式为y=kx+b,则,解得,
故直线PM的表达式为y=x+y0②,
联立①②并整理得:ax2+x﹣y0=0,
则xB+xM=﹣,
即xB﹣p=﹣,则xB=,
将xB的值代入y=ax2得,y=,故点B的坐标为(,),
由点B、A的坐标得,直线AB的表达式为y=x﹣y0,
当x=0时,y=﹣y0,
故直线AB恒过点(0,﹣y0).
14.解:(1)∵抛物线y=x2﹣6x+c,
∴对称轴为直线x=﹣=3;
(2)∵抛物线y=x2﹣6x+c经过点(1,0),
∴1﹣6+c=0,解得c=5,
∴抛物线为y=x2﹣6x+5,
∵y=x2﹣6x+5=(x﹣3)2﹣4,
∴它可以由抛物线y=x2向右平移3个单位,向下平移4个单位而得到;
(3)∵对称轴为直线x=3,与x轴的交点为(1,0),(5,0),与y轴的交点为(0,5)
画出抛物线如图:
15.解:∵当x=﹣1时,二次函数y=x2+6x﹣5的值最小
∴对称轴为直线x=﹣1
∴﹣=﹣1
∵b=6
∴a=3
答:被墨迹污染的二次项系数为3.
16.解:如图,
当点D在OP左侧时,
由∠DPO=∠POB,得DP∥OB,
D与P关于y轴对称,P(1,﹣3),
得D(﹣1,﹣3);
当点D在OP右侧时,延长PD交x轴于点G.
作PH⊥OB于点H,则OH=1,PH=3.
∵∠DPO=∠POB,
∴PG=OG.
设OG=x,则PG=x,HG=x﹣1.
在Rt△PGH中,由x2=(x﹣1)2+32,得x=5.
∴点G(5,0).
∴直线PG的解析式为y=x﹣,
解方程组得或.
∵P(1,﹣3),
∴D(,﹣).
∴点D的坐标为(﹣1,﹣3)或(,﹣).
17.解:在同一坐标系中画出函数y=x2,y=(x+3)2,y=(x﹣3)2﹣1的图象如图:
(1)三个函数的两条相同的特征:①开口方向和大小相同;②都有最小值;
(2)函数y=(x+3)2的图象可由抛物线y=x2向左平移3个单位得到;
(3)函数y=x2的图象可由抛物线y=(x﹣3)2﹣1向上平移1个单位,再向右平移3个单位得到;
(4)函数y=(x+3)2﹣1的图象可由抛物线y=(x﹣3)2怎样向左平移6个单位,向下平移1个单位得到.
18.解:x2+1=kx+2,
x2﹣kx﹣1=0,
x=2k±2,
∴x1=2k﹣2,x2=2k+2,
∴OD=2k+2,OC=2﹣2k,
DC2=(2k+2+2﹣2k)2=16(k2+1),
CF2=22+(2﹣2k)2=8k2﹣8k+8,
DF2=22+(2k+2)2=8k2+8k+8,
∴DC2=CF2+DF2,
∴∠CFD=90°,
故△CFD是直角三角形.
19.解:(1)把(1,5),(3,1)代入函数表达式,得,
解得:;
(2)列表
x ﹣1 0 1 2 3
y 1 4 5 4 1
描点、连线作图如下:
.
20.解:(1)∵D(3,a)为抛物线上一点,
∴a=﹣×32+×3=1,
∴D(3,1)
设直线OD的解析式为y=kx,代入D的坐标得:1=3k,
∴k=,
∴直线OD的解析式为y=x;
(2)过A(1,0)作x轴的垂线,交抛物线y=﹣x2+x于点C,
∴把x=1代入得,y=3,
∴C(1,3),
∴AC=3,
∵点M为直线OD上的一个动点,
∴设M(m,m),
∴N(m,﹣m2+m),
∴MN=|﹣m2+m﹣m|=|﹣4m2+12m|,
∵四边形ACNM为平行四边形,
∴AC=MN,
∴|﹣4m2+12m|=3,
∵0<m<4,
∴﹣4m2+12m>0,
∴﹣4m2+12m=9,
∴m=,
把x=m=代入y=﹣x2+x得n=
∴M(,).
解答题专题训练(附答案)
1.已知抛物线y=ax2+3经过点A(﹣2,﹣13).
(1)求a的值.
(2)若点P(m,﹣22)在此抛物线上,求点P的坐标.
2.已知抛物线y=ax2经过点A(﹣2,﹣8).
(1)求a的值;
(2)若点P(m,﹣6)在此抛物线上,求点P的坐标.
3.抛物线y=a(x﹣2)2经过点(1,﹣1)
(1)确定a的值;
(2)求出该抛物线与坐标轴的交点坐标.
4.如图,平面直角坐标系中,抛物线y=﹣x2+4x+m﹣4(m为常数)与y轴的交点为C,M(3,0)与N(0,﹣2)分别是x轴、y轴上的点
(1)当m=1时,求抛物线顶点坐标.
(2)若3≤x≤3+m时,函数y=﹣x2+4x+m﹣4有最小值﹣7,求m的值.
(3)若抛物线与线段MN有公共点,直接写出m的取值范围是 .
5.如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,…An…将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;
②抛物线依次经过点A1,A2,A3…An,…
(1)分别写出顶点M1,M2,M3的坐标;
(2)顶点M2019的坐标为( , )
6.如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B(1,1).
(1)求m的值;
(2)过动点P(n,0)且垂直于x轴的直线与L1,L2的交点分别为C,D,当点C位于点D上方时,请直接写出n的取值范围.?
7.函数y=ax2与直线y=﹣2x﹣4交于点(2,b).
(1)求a和b的值;
(2)写出抛物线的顶点坐标和对称轴;画出此二次函数的图象;
(3)函数y=ax2,当x取何值时,y随x的增大而增大?
… …
… …
8.如图,已知抛物线y=x2+2x﹣3与x轴的两个交点分别是A、B(A在B的左侧).
(1)求A、B的坐标;
(2)利用函数图象,求当y<5时,x的取值范围.
9.二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1)、B(2,y2)是图象上的两点,你能确定y1与y2的大小关系吗?为什么?
10.若二次函数y=﹣x2图象平移后得到二次函数y=﹣(x﹣2)2+4的图象.
(1)平移的规律是:先向 (填“左”或“右”)平移 个单位,再向 平移 个单位.
(2)在所给的坐标系内画出二次函数y=﹣(x﹣2)2+4的示意图.
11.抛物线y1=ax2+bx+c与直线y2=kx+m的图象如图所示,根据图象回答下列问题:
(1)指出b,b2﹣4ac,a﹣b+c的符号;
(2)若y1<0,指出x的取值范围;
(3)若y1>y2,指出x的取值范围.
12.二次函数y=x2的图象如图所示,点A0位于原点,点B1,B2在y轴的正半轴上,点A1,A2在二次函数y=x2的图象上,若△A0B1A1,△B1A2B2都为等边三角形,求△B1A2B2的边长.
13.如图,点P(O,y0)为y轴正半轴上一定点,点A,B均为y轴右侧抛物线C上两动点,若∠APO=∠BPy,求证:直线AB经过一个定点.
14.抛物线y=x2﹣6x+c的一段如图所示.
(1)求这条抛物线的对称轴;
(2)它可以由抛物线y=x2经过怎样的平移而得到?
(3)画出这条抛物线.
15.这是小明在阅读一本关于函数的课外读物时看到的一段文字,你能写出被墨迹污染的二次项系数吗?
由图象知,当x=﹣1时,二次函数y=x2+6x﹣5的值最小.
16.抛物线y=x2﹣经过P(1,﹣3),B(4,0)两点,若D是抛物线上的一点,满足∠DPO=∠POB,求点D的坐标.
17.在同一坐标系中画出函数y=x2,y=(x+3)2,y=(x﹣3)2﹣1的图象,并回答:
(1)写出这三个函数的两条相同的特征;
(2)函数y=(x+3)2的图象可由抛物线y=x2怎样平移得到?
(3)函数y=x2的图象可由抛物线y=(x﹣3)2﹣1怎样平移得到?
(4)函数y=(x+3)2﹣1的图象可由抛物线y=(x﹣3)2怎样平移得到?
18.如图,动直线y=kx+2(k>0)与y轴交于点F,与抛物线y=相交于A,B两点,过点A,B分别作x轴的垂线,垂足分别为点C,D,连接CF,DF,请你判断△CDF的形状,并说明理由.
19.已知二次函数y=﹣x2+bx+c经过点(1,5),(3,1).
(1)求b,c的值;
(2)在所给平面直角坐标系中画出该函数的图象(要求列表、描述、连线)
20.如图,过A(1,0)作x轴的垂线,交抛物线y=﹣x2+x于点C.D(3,a)为抛物线上一点,点M为线段OD上的一个动点,MN∥AC交抛物线于点N.
(1)求直线OD的解析式;
(2)若四边形ACNM为平行四边形,求点M的坐标.
参考答案
1.解:(1)将点A(﹣2,﹣13).代入y=ax2+3,得﹣13=4a+3,
解得a=﹣4,
∴抛物线的函数解析式为y=﹣4x2+3,
(2)∵点P(m,﹣22)在此抛物线上,
∴﹣22=﹣4m2+3,
解得m=±,
∴点P的坐标为(,﹣22)或(﹣,﹣22).
2.解:(1)把点A(﹣2,﹣8)代入y=ax2,
得4a=﹣8,
∴a=﹣2;
(2)把点P(m,﹣6)代入y=﹣2x2中,
得﹣2m2=﹣6,
∴m=±,
∴P(,﹣6).
3.解:(1)把(1,﹣1)代入y=a(x﹣2)2得a (1﹣2)2=﹣1
解得a=﹣1
(2)抛物线解析式为y=﹣(x﹣2)2,
当y=0时,﹣(x﹣2)2=0,解得x=2,
所以抛物线与x轴交点坐标为(2,0);
当x=0时,y=﹣(x﹣2)2=﹣4,
所以抛物线与y轴交点坐标为(0,﹣4).
4.解:(1)当m=1时,y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴顶点坐标为(2,1);
(2)由抛物线y=﹣x2+4x+m﹣4(m为常数)可知:开口向上,函数的对称轴为直线x=2,
∴当3≤x≤3+m时,y随x的增大而减小,
∴当x=m+3时,y有最小值﹣7,
∴﹣(m+3)2+4(m+3)+m﹣4=﹣7,
解得m1=2,m2=﹣3(舍去),
∴m=2;
(3)∵M(3,0),N(0,﹣2),
∴直线MN的解析式为y=x﹣2,
∵抛物线与线段MN有公共点,则方程﹣x2+4x+m﹣4=x﹣2,即x2﹣x﹣m+2=0中△≥0,且m﹣4≤﹣2,
∴(﹣)2﹣4(﹣m+2)≥0,
解得﹣≤m≤2,
故答案为﹣≤m≤2.
5.解:(1)∵抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,…,An,…,
∴点An的坐标为(n,n2).
设点Mn的坐标为(a,a),则以点Mn为顶点的抛物线解析式为y=(x﹣a)2+a,
∵点An(n,n2)在抛物线y=(x﹣a)2+a上,
∴n2=(n﹣a)2+a,解得:a=2n﹣1或a=0(舍去),
∴Mn的坐标为(2n﹣1,2n﹣1),
∴顶点M1的坐标为(1,1),顶点M2的坐标为(3,3),顶点M3的坐标为(5,5);
(2)∵Mn的坐标为(2n﹣1,2n﹣1),
∴点M2019,两坐标为:2019×2﹣1=4037,
∴M2019(4037,4037),
故答案为:4037,4037.
6.解:(1)把B(1,1)代入y=ax2得:a=1,
∴抛物线解析式为y=x2.
把A(m,4)代入y=x2得:4=m2,
∴m=±2.
∵点A在二象限,
∴m=﹣2.
(2)观察函数图象可知:当﹣2<x<1时,直线在抛物线的上方,
∴n的取值范围为:﹣2<n<1.
7.解:(1)把(2,b)代入y=﹣2x﹣4得b=﹣4﹣4=﹣8,
把(2,﹣8)代入y=ax2得4a=﹣8,解得a=﹣2;
(2)抛物线y=﹣2x2的顶点坐标为(0,0),对称轴为y轴,
列表:
x … ﹣1.5 ﹣1 ﹣0.5 0 0.5 1 1.5 …
y … ﹣4.5 ﹣2 ﹣0.5 0 ﹣0.5 ﹣2 ﹣4.5 …
描点,连线,如图:
(3)当x<0时,y随x的增大而增大.
8.解:(1)当x2+2x﹣3=0时,解得x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0);
(2)当y=5时,x2+2x﹣3=5,
整理得x2+2x﹣8=0,
解得x1=﹣4,x2=2,
由函数图象可得,当﹣4<x<2时,y<5.
9.解:能定y1与y2的大小关系.
因为抛物线的开口向下,对称轴为直线x=﹣3,
所以当x>﹣3时,y随x的增大而减小,
因为1<2,
所以y1>y2.
10.解:(1)原抛物线的顶点坐标为(0,0),新抛物线的顶点坐标为(2,4),说明新抛物线向右移动了2个单位,向上移动了4个单位.
(2)抓住顶点(2,4),与y轴(0,0),x轴的交点(4,0)(0,0)等关键点来画.
11.解:(1)∵二次函数开口向上a>0,﹣>0,得出b<0,
∴b<0,
∵二次函数与坐标轴的交点个数为2,
∴b2﹣4ac>0,
∵x=﹣1时,y=a﹣b+c,结合图象可知,
∴a﹣b+c>0;
(2)结合图象可知,
当1<x<4 时,y1<0;
(3)结合图象可知,
当x<1 或 x>5时,y1>y2.
12.解:设△A0B1A1的边长为a,△B1B2A2的边长为b,则点A1的坐标为(a,a),点A2的坐标为(b,a+b).
∵点A1、A2在二次函数y=x2的图象上,
∴,
解得:或(不合题意,舍去),
∴△B1A2B2的边长为4.
13.证明:设抛物线的表达式为y=ax2①,
作点A关于y轴的对称轴M,
∵抛物线关于y轴对称,故点M在抛物线上,连接MP,
∵∠MPO=∠OPA=∠BPy,故M、P、B三点共线,
设点A(p,ap2),则点M(﹣p,ap2),
设直线PM的表达式为y=kx+b,则,解得,
故直线PM的表达式为y=x+y0②,
联立①②并整理得:ax2+x﹣y0=0,
则xB+xM=﹣,
即xB﹣p=﹣,则xB=,
将xB的值代入y=ax2得,y=,故点B的坐标为(,),
由点B、A的坐标得,直线AB的表达式为y=x﹣y0,
当x=0时,y=﹣y0,
故直线AB恒过点(0,﹣y0).
14.解:(1)∵抛物线y=x2﹣6x+c,
∴对称轴为直线x=﹣=3;
(2)∵抛物线y=x2﹣6x+c经过点(1,0),
∴1﹣6+c=0,解得c=5,
∴抛物线为y=x2﹣6x+5,
∵y=x2﹣6x+5=(x﹣3)2﹣4,
∴它可以由抛物线y=x2向右平移3个单位,向下平移4个单位而得到;
(3)∵对称轴为直线x=3,与x轴的交点为(1,0),(5,0),与y轴的交点为(0,5)
画出抛物线如图:
15.解:∵当x=﹣1时,二次函数y=x2+6x﹣5的值最小
∴对称轴为直线x=﹣1
∴﹣=﹣1
∵b=6
∴a=3
答:被墨迹污染的二次项系数为3.
16.解:如图,
当点D在OP左侧时,
由∠DPO=∠POB,得DP∥OB,
D与P关于y轴对称,P(1,﹣3),
得D(﹣1,﹣3);
当点D在OP右侧时,延长PD交x轴于点G.
作PH⊥OB于点H,则OH=1,PH=3.
∵∠DPO=∠POB,
∴PG=OG.
设OG=x,则PG=x,HG=x﹣1.
在Rt△PGH中,由x2=(x﹣1)2+32,得x=5.
∴点G(5,0).
∴直线PG的解析式为y=x﹣,
解方程组得或.
∵P(1,﹣3),
∴D(,﹣).
∴点D的坐标为(﹣1,﹣3)或(,﹣).
17.解:在同一坐标系中画出函数y=x2,y=(x+3)2,y=(x﹣3)2﹣1的图象如图:
(1)三个函数的两条相同的特征:①开口方向和大小相同;②都有最小值;
(2)函数y=(x+3)2的图象可由抛物线y=x2向左平移3个单位得到;
(3)函数y=x2的图象可由抛物线y=(x﹣3)2﹣1向上平移1个单位,再向右平移3个单位得到;
(4)函数y=(x+3)2﹣1的图象可由抛物线y=(x﹣3)2怎样向左平移6个单位,向下平移1个单位得到.
18.解:x2+1=kx+2,
x2﹣kx﹣1=0,
x=2k±2,
∴x1=2k﹣2,x2=2k+2,
∴OD=2k+2,OC=2﹣2k,
DC2=(2k+2+2﹣2k)2=16(k2+1),
CF2=22+(2﹣2k)2=8k2﹣8k+8,
DF2=22+(2k+2)2=8k2+8k+8,
∴DC2=CF2+DF2,
∴∠CFD=90°,
故△CFD是直角三角形.
19.解:(1)把(1,5),(3,1)代入函数表达式,得,
解得:;
(2)列表
x ﹣1 0 1 2 3
y 1 4 5 4 1
描点、连线作图如下:
.
20.解:(1)∵D(3,a)为抛物线上一点,
∴a=﹣×32+×3=1,
∴D(3,1)
设直线OD的解析式为y=kx,代入D的坐标得:1=3k,
∴k=,
∴直线OD的解析式为y=x;
(2)过A(1,0)作x轴的垂线,交抛物线y=﹣x2+x于点C,
∴把x=1代入得,y=3,
∴C(1,3),
∴AC=3,
∵点M为直线OD上的一个动点,
∴设M(m,m),
∴N(m,﹣m2+m),
∴MN=|﹣m2+m﹣m|=|﹣4m2+12m|,
∵四边形ACNM为平行四边形,
∴AC=MN,
∴|﹣4m2+12m|=3,
∵0<m<4,
∴﹣4m2+12m>0,
∴﹣4m2+12m=9,
∴m=,
把x=m=代入y=﹣x2+x得n=
∴M(,).
