13.3《等腰三角形》同步练习 2021-2022学年华东师大版八年级数学上册(Word版含答案)
文档属性
| 名称 | 13.3《等腰三角形》同步练习 2021-2022学年华东师大版八年级数学上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 79.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 22:11:25 | ||
图片预览


文档简介
2021年华师大版数学八年级上册
13.3《等腰三角形》同步练习卷
一、选择题
1.一个等腰三角形的一边长是7cm,另一边长为5cm,那么这个等腰三角形的周长是( )
A.12cm B.17cm C.19cm D.17cm或19cm
2.如果等腰三角形的一个底角为α,那么( )
A.α不大于45° B.0°<α<90° C.α不大于90° D.45°<α<90°
3.如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )
A.12 B.4 C.8 D.不确定
4.等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55° B.70°,40°或70°,55°
C.70°,40° D.55°,55°或70°,40°
5.如图,在△ABC中,∠A=36°,∠C=72°,∠ABC平分线交AC于D,则图中共有等腰三角形( )
A.0个 B.1个 C.2个 D.3个
6.在△ABC中,AB=c,BC=a,AC=b,下列条件不能判定△ABC是等腰三角形的是( )
A.∠A∶∠B∶∠C=1∶1∶3
B.a∶b∶c=2∶2∶3
C.∠B=50°,∠C=80°
D.2∠A=∠B+∠C
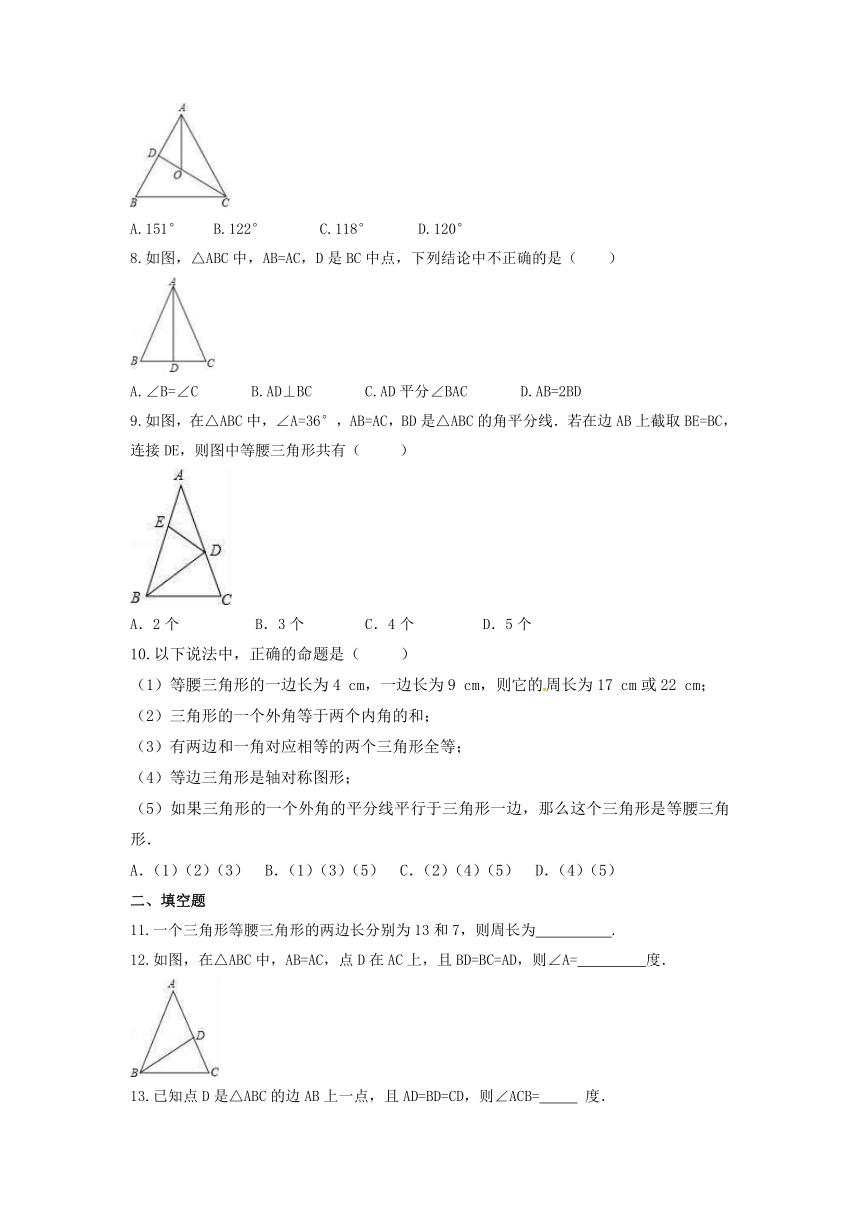
7.如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的垂直平分线交于点O,连接OC,则∠AOC的度数为( )
A.151° B.122° C.118° D.120°
8.如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )
A.∠B=∠C B.AD⊥BC C.AD平分∠BAC D.AB=2BD
9.如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
A.2个 B.3个 C.4个 D.5个
10.以下说法中,正确的命题是( )
(1)等腰三角形的一边长为4 cm,一边长为9 cm,则它的周长为17 cm或22 cm;
(2)三角形的一个外角等于两个内角的和;
(3)有两边和一角对应相等的两个三角形全等;
(4)等边三角形是轴对称图形;
(5)如果三角形的一个外角的平分线平行于三角形一边,那么这个三角形是等腰三角形.
A.(1)(2)(3) B.(1)(3)(5) C.(2)(4)(5) D.(4)(5)
二、填空题
11.一个三角形等腰三角形的两边长分别为13和7,则周长为 .
12.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A= 度.
13.已知点D是△ABC的边AB上一点,且AD=BD=CD,则∠ACB= 度.
14.若等腰三角形的一个内角为50°,则它的顶角为 。
15.如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .
16.如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F.
给出下列四个结论:
①AE=CF;
②△EPF是等腰直角三角形;
③EF=AB;
④,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合).
上述结论中始终正确的有________(把你认为正确的结论的序号都填上)。
三、解答题
17.用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长分别是多少?
(2)能围成一边的长为4cm的等腰三角形吗?
18.如图所示,已知在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
19.如图,△ACB和△ADE均为等边三角形,点C、E、D在同一直线上,连接BD,试猜想线段CE、BD之间的数量关系,并说明理由.
20.如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.
(1)判断△DBC的形状并证明你的结论.
(2)求证:BF=AC.
(3)试说明BF=2CE.
参考答案
1.D
2.B
3.C
4.D
5.D.
6.D.
7.B.
8.D.
9.D
10.D
11.答案为:33或27.
12.答案为:36.
13.答案为:90.
14.答案为:80°或50°;
15.答案为:50°.
16.答案为:①②④
17.解:(1)腰长为7.2cm,底边长为3.6cm;
(2)能围成底边长为4cm的等腰三角形
18.解:在△ABC中,AB=AD=DC,
∵AB=AD,在三角形ABD中,
∠B=∠ADB=(180°﹣26°)×=77°,
又∵AD=DC,
在三角形ADC中,
∴∠C==77°×=38.5°.
19.解:CE=BD,
理由:∵△ACB和△ADE均为等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠DAB=∠EAC.
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
∴CE=BD.
20.解:(1)△DBC是等腰直角三角形,理由:
∵∠ABC=45°,CD⊥AB,
∴∠BCD=45°,
∴BD=CD,
∴△DBC是等腰直角三角形;
(2)∵BE⊥AC,
∴∠BDC=∠BEC=90°,
∵∠BFD=∠CFE,
∴∠DBF=∠DCA,
在△BDF与△CDA中,
,
∴△BDF≌△CDA(ASA),
∴BF=AC;
(3)∵BE是AC的垂直平分线,
∴AC=2CE,
∴BF=2CE.
13.3《等腰三角形》同步练习卷
一、选择题
1.一个等腰三角形的一边长是7cm,另一边长为5cm,那么这个等腰三角形的周长是( )
A.12cm B.17cm C.19cm D.17cm或19cm
2.如果等腰三角形的一个底角为α,那么( )
A.α不大于45° B.0°<α<90° C.α不大于90° D.45°<α<90°
3.如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )
A.12 B.4 C.8 D.不确定
4.等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55° B.70°,40°或70°,55°
C.70°,40° D.55°,55°或70°,40°
5.如图,在△ABC中,∠A=36°,∠C=72°,∠ABC平分线交AC于D,则图中共有等腰三角形( )
A.0个 B.1个 C.2个 D.3个
6.在△ABC中,AB=c,BC=a,AC=b,下列条件不能判定△ABC是等腰三角形的是( )
A.∠A∶∠B∶∠C=1∶1∶3
B.a∶b∶c=2∶2∶3
C.∠B=50°,∠C=80°
D.2∠A=∠B+∠C
7.如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的垂直平分线交于点O,连接OC,则∠AOC的度数为( )
A.151° B.122° C.118° D.120°
8.如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )
A.∠B=∠C B.AD⊥BC C.AD平分∠BAC D.AB=2BD
9.如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
A.2个 B.3个 C.4个 D.5个
10.以下说法中,正确的命题是( )
(1)等腰三角形的一边长为4 cm,一边长为9 cm,则它的周长为17 cm或22 cm;
(2)三角形的一个外角等于两个内角的和;
(3)有两边和一角对应相等的两个三角形全等;
(4)等边三角形是轴对称图形;
(5)如果三角形的一个外角的平分线平行于三角形一边,那么这个三角形是等腰三角形.
A.(1)(2)(3) B.(1)(3)(5) C.(2)(4)(5) D.(4)(5)
二、填空题
11.一个三角形等腰三角形的两边长分别为13和7,则周长为 .
12.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A= 度.
13.已知点D是△ABC的边AB上一点,且AD=BD=CD,则∠ACB= 度.
14.若等腰三角形的一个内角为50°,则它的顶角为 。
15.如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .
16.如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F.
给出下列四个结论:
①AE=CF;
②△EPF是等腰直角三角形;
③EF=AB;
④,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合).
上述结论中始终正确的有________(把你认为正确的结论的序号都填上)。
三、解答题
17.用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长分别是多少?
(2)能围成一边的长为4cm的等腰三角形吗?
18.如图所示,已知在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
19.如图,△ACB和△ADE均为等边三角形,点C、E、D在同一直线上,连接BD,试猜想线段CE、BD之间的数量关系,并说明理由.
20.如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.
(1)判断△DBC的形状并证明你的结论.
(2)求证:BF=AC.
(3)试说明BF=2CE.
参考答案
1.D
2.B
3.C
4.D
5.D.
6.D.
7.B.
8.D.
9.D
10.D
11.答案为:33或27.
12.答案为:36.
13.答案为:90.
14.答案为:80°或50°;
15.答案为:50°.
16.答案为:①②④
17.解:(1)腰长为7.2cm,底边长为3.6cm;
(2)能围成底边长为4cm的等腰三角形
18.解:在△ABC中,AB=AD=DC,
∵AB=AD,在三角形ABD中,
∠B=∠ADB=(180°﹣26°)×=77°,
又∵AD=DC,
在三角形ADC中,
∴∠C==77°×=38.5°.
19.解:CE=BD,
理由:∵△ACB和△ADE均为等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠DAB=∠EAC.
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
∴CE=BD.
20.解:(1)△DBC是等腰直角三角形,理由:
∵∠ABC=45°,CD⊥AB,
∴∠BCD=45°,
∴BD=CD,
∴△DBC是等腰直角三角形;
(2)∵BE⊥AC,
∴∠BDC=∠BEC=90°,
∵∠BFD=∠CFE,
∴∠DBF=∠DCA,
在△BDF与△CDA中,
,
∴△BDF≌△CDA(ASA),
∴BF=AC;
(3)∵BE是AC的垂直平分线,
∴AC=2CE,
∴BF=2CE.
