第26章解直角三角形达标测试卷2021-2022学年 九年级数学冀教版上册(Word版含答案)
文档属性
| 名称 | 第26章解直角三角形达标测试卷2021-2022学年 九年级数学冀教版上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 235.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 22:28:15 | ||
图片预览



文档简介
第二十六章达标测试卷
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.cos 45°的值为( )
A. B. C. D.1
2.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sin α=,则t的值是( )
A.4 B.6 C.2 D.2
(第2题) (第3题)
3.如图,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O,则图中线段的比不能表示sin A的式子为( )
A. B. C. D.
4.如图,已知点C从点B出发,沿射线BD方向运动,运动到点D停止,则在这个过程中,从点A观测点C的俯角将( )
A.增大 B.减小
C.先增大后减小 D先减小后增大
(第4题) (第5题) (第6题)
5.如图,A,B,C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC′B′,则tan B′的值为( )
A. B. C. D.
6.课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24 m,那么旗杆AB的高度是( )
A.12 m B.8 m C.24 m D.24 m
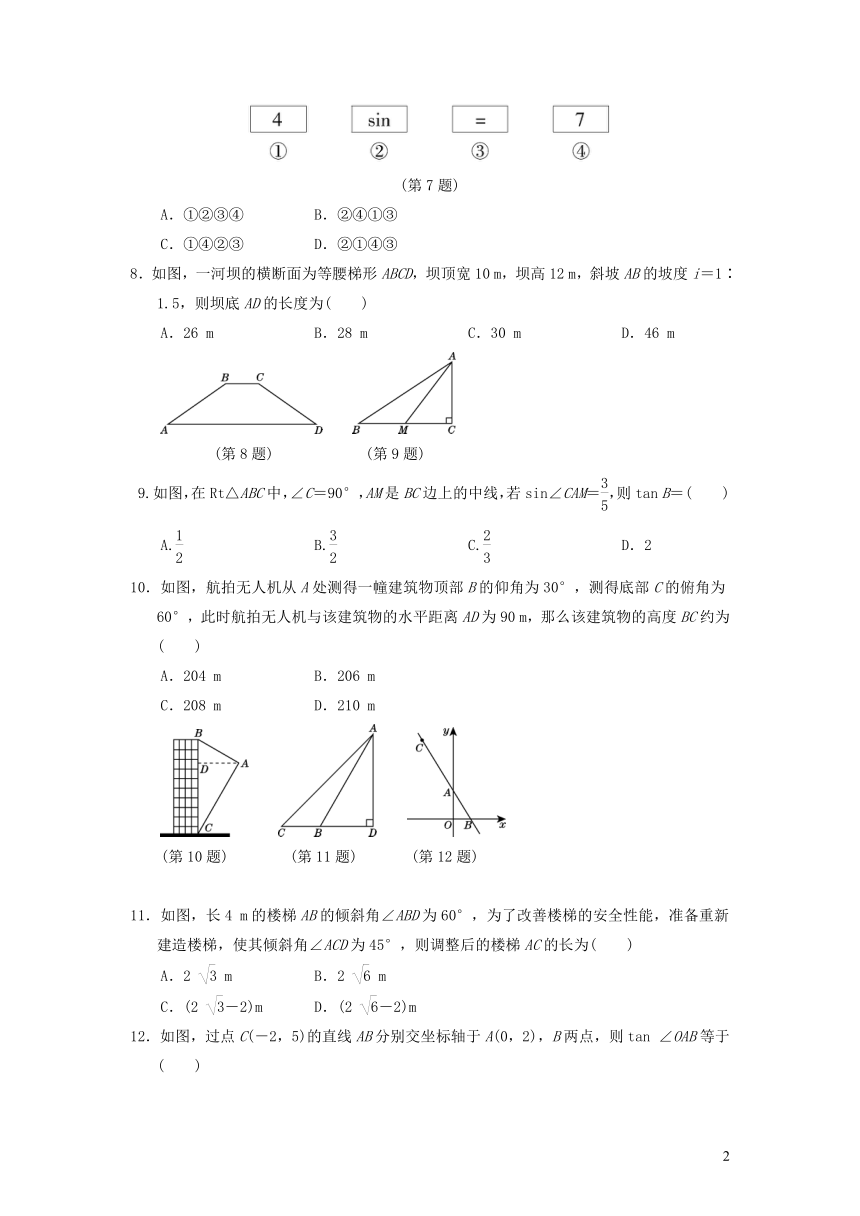
7.若计算器的四个键如图所示,在角的度量单位为“度”的情况下,用计算器求sin 47°,正确的按键顺序是( )
(第7题)
A.①②③④ B.②④①③
C.①④②③ D.②①④③
8.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10 m,坝高12 m,斜坡AB的坡度i=1∶1.5,则坝底AD的长度为( )
A.26 m B.28 m C.30 m D.46 m
(第8题) (第9题)
9.如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,若sin∠CAM=,则tan B=( )
A. B. C. D.2
10.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90 m,那么该建筑物的高度BC约为( )
A.204 m B.206 m
C.208 m D.210 m
(第10题) (第11题) (第12题)
11.如图,长4 m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
A.2 m B.2 m
C.(2 -2)m D.(2 -2)m
12.如图,过点C(-2,5)的直线AB分别交坐标轴于A(0,2),B两点,则tan ∠OAB等于( )
A. B.
C. D.
13.如图,一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为10 海里,渔船将险情报告发给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,30分钟后,救援船在海岛C处恰好与渔船相遇,那么救援船航行的速度为( )
A.10 海里/时 B.15海里/时
C.5 海里/时 D.30海里/时
(第13题) (第14题)
14.如图,在Rt△ABC中,∠B=90°,∠BAC=30°,以点A为圆心,BC的长为半径画弧交AB于点D,分别以点A,D为圆心,AB的长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
A. B. C. D.
15.如图,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sin A=,则下列结论:①DE=3 cm;②BE=1 cm;③菱形的面积为15 cm2;④BD=2 cm.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
(第15题) (第16题)
16.“五一”期间,小明和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔DE的高度.如图,他从点D处走到点A处,然后沿着斜坡AB从点A处走了8 m到达点B处,此时回望观景塔,更显气势宏伟.在B点测得观景塔顶端的仰角为45°且AB⊥BE,再往前走到点C处,测得观景塔顶端的仰角为30°,B,C之间的水平距离BC=10 m,则观景塔DE的高度约为(精确到1 m,≈1.41,≈1.73)( )
A.14 m B.15 m
C.19 m D.20 m
二、填空题(17、18题每题3分,19题每空2分,共12分)
17.在△ABC中,若+(1-tan B)2=0,则∠C的度数是________.
18.如图,八个完全相同的小长方形恰好能拼成一个边长为4的正方形,连接小长方形的顶点得△ABC,则tan ∠ACB=________.
(第18题) (第19题)
19.如图①,在边长为1的正方形网格中,连接格点A,B和C,D,AB和CD相交于点P,求tan∠CPB的值.嘉琪同学是这样解决的:连接格点A,D,可得△ADC为等腰直角三角形,则AD⊥CD,又∠CPB=∠APD,那么∠CPB就变换到Rt△ADP中.由BD∥AC,可得DPPC=________,则tan∠CPB的值为________.
【探索延伸】如图②,在边长为1的正方形网格中,AB和CD相交于点P,则sin∠APD的值为________.
三、解答题(20、21题每题8分,22、23题每题9分,24、25题每题10分,26题12分,共66分)
20.计算:
(1)(-2)3+-2sin 30°+(2 020-π)0;
(2)sin2 45°-cos 60°-+2sin2 60°·tan 60°.
21.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.已知2a=3b,求∠B的正弦、余弦和正切值.
22.如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
(第22题)
(1)若∠A=60°,求BC的长;
(2)若sin A=,求AD的长.
23.如图,某山山脚下西端A处与东端B处相距800(1+)m,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为 m/s.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
(第23题)
24.如图,在△ABC中,tan (∠C-∠B)=,AC=,AB=5,求BC的长.
(第24题)
25.某校为检测师生体温,安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面2.2 m,为了解自己的有效测温区间,身高1.6 m的小聪做了如下试验:当他在地面N处时,测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;当他在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算结果精确到0.1 m,sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)
(第25题)
26.在△ABC中,∠ABC=90°,tan∠BAC=.
(1)如图①,分别过A,C两点作经过点B的直线的垂线,垂足分别为M,N,若点B恰好是线段MN的中点,求tan∠BAM的值;
(2)如图②,P是边BC延长线上一点,∠APB=∠BAC,求tan∠PAC的值.
(第26题)
答案
一、1.B 2.D 3.C 4.A 5.B 6.B
7.D 8.D 9.C 10.C 11.B 12.B
13.D
14.B 【点拨】设BC=x.在Rt△ABC中,∠B=90°,∠BAC=30°,
∴AB=BC=x.
根据题意,得AD=BC=x,AE=DE=AB=x.
如图,过点E作EM⊥AD于点M,易知AM=AD=x.
在Rt△AEM中,cos ∠EAD===.
(第14题)
15.C
16.C 【点拨】过点B作BF⊥DE于F,过点A作AH⊥BF于H,易知DF=AH.
∵∠EBF=45°,AB⊥BE,
∴∠ABH=45°.
∴DF=AH=8×=4 ( m).
在Rt△ECF中,tan∠ECF=,
∴CF=EF.
在Rt△EBF中,∠EBF=45°,
∴BF=EF.
∵CF-BF=BC,∴EF-EF=10 m,
解得EF=(5 +5) m,
∴DE=EF+DF=5 +5+4 ≈19(m).
二、17.75°
18. 【点拨】由正方形的边长为4,易得小长方形的长为2,宽为1.如图,延长CA,交正方形一边于点D,连接DB,易得BD⊥AC,DB=,DC=3 ,∴tan∠ACB==.
(第18题)
19.1?2;3;
【点拨】如图,连接CE,DE,过D作DM⊥CE于点M.
(第19题)
∵BC∥AE,BC=AE,
∴四边形ABCE是平行四边形,
∴CE∥AB,∴∠APD=∠ECD.
∵△ECD的面积=3×4-×1×4-×2×3-×1×3=,
∴CE·DM=.
易得CE=,∴DM=,
易得CD=,
∴sin ∠APD=sin ∠ECD==.
三、20.解:(1)原式=-8+4-2×+1=-8+4-1+1=-4.
(2)原式=()2--+2×()2×=.
21.解:由2a=3b,可得=.
设a=3k(k>0),则b=2k,
由勾股定理,得c===k,
∴sin B===,
cos B===,
tan B===.
22.解:(1)在Rt△ABE中,∵∠A=60°,∠ABE=90°,AB=6,tan A=,
∴∠E=30°,BE=AB·tan A=6×tan 60°=6 .
在Rt△CDE中,∵∠CDE=90°,CD=4,
∴CE=2CD=8.
∴BC=BE-CE=6 -8.
(2)在Rt△ABE中,sin A==,
∴可设BE=4x(x>0),则AE=5x.
由勾股定理可得AB=3x,
∴3x=6,解得x=2.
∴BE=8,AE=10.
易得tan E==,∴=,
解得DE=.
∴AD=AE-DE=10-=.
23.解:过点C作CD⊥AB于点D,设AD=x m,小明的行走速度是a m/s.
∵∠A=45°,CD⊥AB,
∴CD=AD=x m,AC=x m.
在Rt△BCD中,∵∠B=30°,
∴BC===2x(m).
∵小军的行走速度为 m/s,小明与小军同时到达山顶C处,
∴=,解得a=1.
答:小明的行走速度是1 m/s.
24.解:如图,在BC上取一点E,使AE=AC=,连接AE,过点E作EF⊥AB于点F,过点A作AD⊥CE于点D,
则∠AEC=∠C,DE=CD.
(第24题)
∵∠EAF=∠AEC-∠B,
∴∠EAF=∠C-∠B.
∵tan(∠C-∠B)=,
∴tan∠EAF=,即=,
设EF=6x,则AF=17x,由勾股定理得AF2+EF2=AE2,
∴(17x)2+(6x)2=()2,
∴x=(负值舍去),
∴EF=,AF=,
∴BF=AB-AF=5-=,
∴BE===2.
∵S△ABE=AB·EF=BE·AD,
∴AD===3,
∴CD=DE==2,
∴BC=BE+DE+CD=2+2+2=6.
25.解:如图,连接BC并延长BC交AD于点E,易知DE=1.6 m,则AE=AD-DE=0.6 m.
在Rt△ABE中,BE=≈≈1.88 (m),
在Rt△ACE中,CE=≈≈0.35 (m).
易知四边形MNBC是矩形,
∴MN=BC=BE-CE≈1.88-0.35≈1.5 (m).
答:小聪在地面的有效测温区间MN的长度约为1.5 m.
(第25题)
26.解:(1)∵AM⊥MN,CN⊥MN,
∴∠M=∠N=90°,
∴∠MAB+∠ABM=90°.
∵∠ABC=90°,
∴∠NBC+∠ABM=90°,
∴∠MAB=∠NBC,
∴△AMB∽△BNC,
∴==tan∠BAC=.
∵点B是线段MN的中点,
∴BM=BN,
∴在Rt△AMB中,tan∠BAM===.
(2)过点C作CD⊥AC交AP于点D,
过点D作DE⊥BP于点E.
∵tan∠BAC=,∠APB=∠BAC,
∴tan∠BAC==,
tan∠APB==.
设BC=x,则AB=2x,BP=4x,
∴CP=BP-BC=4x-x=3x.
易得∠BAC=∠ECD,
∴∠APB=∠ECD.
∵DE⊥BP,
∴CE=EP=CP=x.
∵∠BAC=∠ECD,∠B=∠CED=90°,
∴△ABC∽△CED,
∴===,
∴在Rt△ACD中,tan∠PAC==.
4
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.cos 45°的值为( )
A. B. C. D.1
2.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sin α=,则t的值是( )
A.4 B.6 C.2 D.2
(第2题) (第3题)
3.如图,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O,则图中线段的比不能表示sin A的式子为( )
A. B. C. D.
4.如图,已知点C从点B出发,沿射线BD方向运动,运动到点D停止,则在这个过程中,从点A观测点C的俯角将( )
A.增大 B.减小
C.先增大后减小 D先减小后增大
(第4题) (第5题) (第6题)
5.如图,A,B,C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC′B′,则tan B′的值为( )
A. B. C. D.
6.课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24 m,那么旗杆AB的高度是( )
A.12 m B.8 m C.24 m D.24 m
7.若计算器的四个键如图所示,在角的度量单位为“度”的情况下,用计算器求sin 47°,正确的按键顺序是( )
(第7题)
A.①②③④ B.②④①③
C.①④②③ D.②①④③
8.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10 m,坝高12 m,斜坡AB的坡度i=1∶1.5,则坝底AD的长度为( )
A.26 m B.28 m C.30 m D.46 m
(第8题) (第9题)
9.如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,若sin∠CAM=,则tan B=( )
A. B. C. D.2
10.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90 m,那么该建筑物的高度BC约为( )
A.204 m B.206 m
C.208 m D.210 m
(第10题) (第11题) (第12题)
11.如图,长4 m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
A.2 m B.2 m
C.(2 -2)m D.(2 -2)m
12.如图,过点C(-2,5)的直线AB分别交坐标轴于A(0,2),B两点,则tan ∠OAB等于( )
A. B.
C. D.
13.如图,一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为10 海里,渔船将险情报告发给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,30分钟后,救援船在海岛C处恰好与渔船相遇,那么救援船航行的速度为( )
A.10 海里/时 B.15海里/时
C.5 海里/时 D.30海里/时
(第13题) (第14题)
14.如图,在Rt△ABC中,∠B=90°,∠BAC=30°,以点A为圆心,BC的长为半径画弧交AB于点D,分别以点A,D为圆心,AB的长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
A. B. C. D.
15.如图,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sin A=,则下列结论:①DE=3 cm;②BE=1 cm;③菱形的面积为15 cm2;④BD=2 cm.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
(第15题) (第16题)
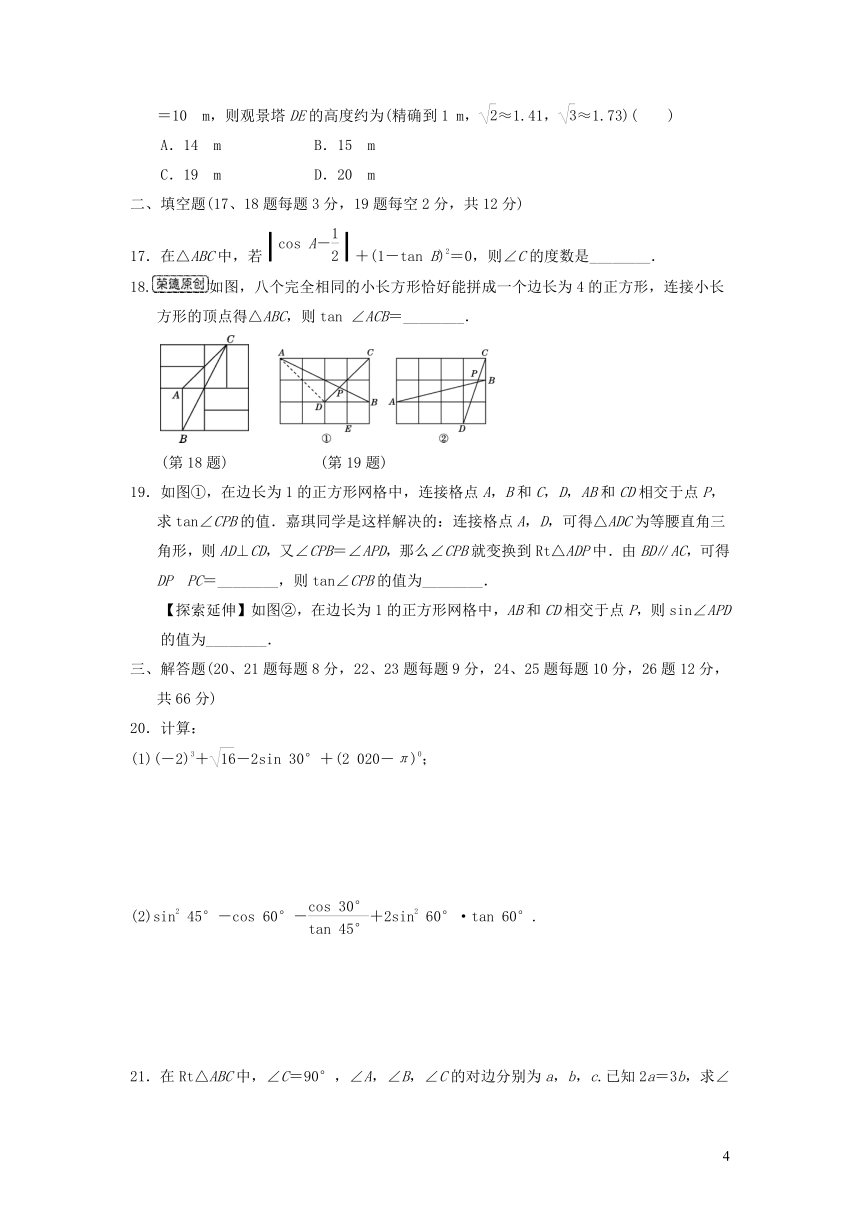
16.“五一”期间,小明和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔DE的高度.如图,他从点D处走到点A处,然后沿着斜坡AB从点A处走了8 m到达点B处,此时回望观景塔,更显气势宏伟.在B点测得观景塔顶端的仰角为45°且AB⊥BE,再往前走到点C处,测得观景塔顶端的仰角为30°,B,C之间的水平距离BC=10 m,则观景塔DE的高度约为(精确到1 m,≈1.41,≈1.73)( )
A.14 m B.15 m
C.19 m D.20 m
二、填空题(17、18题每题3分,19题每空2分,共12分)
17.在△ABC中,若+(1-tan B)2=0,则∠C的度数是________.
18.如图,八个完全相同的小长方形恰好能拼成一个边长为4的正方形,连接小长方形的顶点得△ABC,则tan ∠ACB=________.
(第18题) (第19题)
19.如图①,在边长为1的正方形网格中,连接格点A,B和C,D,AB和CD相交于点P,求tan∠CPB的值.嘉琪同学是这样解决的:连接格点A,D,可得△ADC为等腰直角三角形,则AD⊥CD,又∠CPB=∠APD,那么∠CPB就变换到Rt△ADP中.由BD∥AC,可得DPPC=________,则tan∠CPB的值为________.
【探索延伸】如图②,在边长为1的正方形网格中,AB和CD相交于点P,则sin∠APD的值为________.
三、解答题(20、21题每题8分,22、23题每题9分,24、25题每题10分,26题12分,共66分)
20.计算:
(1)(-2)3+-2sin 30°+(2 020-π)0;
(2)sin2 45°-cos 60°-+2sin2 60°·tan 60°.
21.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.已知2a=3b,求∠B的正弦、余弦和正切值.
22.如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
(第22题)
(1)若∠A=60°,求BC的长;
(2)若sin A=,求AD的长.
23.如图,某山山脚下西端A处与东端B处相距800(1+)m,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为 m/s.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
(第23题)
24.如图,在△ABC中,tan (∠C-∠B)=,AC=,AB=5,求BC的长.
(第24题)
25.某校为检测师生体温,安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面2.2 m,为了解自己的有效测温区间,身高1.6 m的小聪做了如下试验:当他在地面N处时,测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;当他在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算结果精确到0.1 m,sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)
(第25题)
26.在△ABC中,∠ABC=90°,tan∠BAC=.
(1)如图①,分别过A,C两点作经过点B的直线的垂线,垂足分别为M,N,若点B恰好是线段MN的中点,求tan∠BAM的值;
(2)如图②,P是边BC延长线上一点,∠APB=∠BAC,求tan∠PAC的值.
(第26题)
答案
一、1.B 2.D 3.C 4.A 5.B 6.B
7.D 8.D 9.C 10.C 11.B 12.B
13.D
14.B 【点拨】设BC=x.在Rt△ABC中,∠B=90°,∠BAC=30°,
∴AB=BC=x.
根据题意,得AD=BC=x,AE=DE=AB=x.
如图,过点E作EM⊥AD于点M,易知AM=AD=x.
在Rt△AEM中,cos ∠EAD===.
(第14题)
15.C
16.C 【点拨】过点B作BF⊥DE于F,过点A作AH⊥BF于H,易知DF=AH.
∵∠EBF=45°,AB⊥BE,
∴∠ABH=45°.
∴DF=AH=8×=4 ( m).
在Rt△ECF中,tan∠ECF=,
∴CF=EF.
在Rt△EBF中,∠EBF=45°,
∴BF=EF.
∵CF-BF=BC,∴EF-EF=10 m,
解得EF=(5 +5) m,
∴DE=EF+DF=5 +5+4 ≈19(m).
二、17.75°
18. 【点拨】由正方形的边长为4,易得小长方形的长为2,宽为1.如图,延长CA,交正方形一边于点D,连接DB,易得BD⊥AC,DB=,DC=3 ,∴tan∠ACB==.
(第18题)
19.1?2;3;
【点拨】如图,连接CE,DE,过D作DM⊥CE于点M.
(第19题)
∵BC∥AE,BC=AE,
∴四边形ABCE是平行四边形,
∴CE∥AB,∴∠APD=∠ECD.
∵△ECD的面积=3×4-×1×4-×2×3-×1×3=,
∴CE·DM=.
易得CE=,∴DM=,
易得CD=,
∴sin ∠APD=sin ∠ECD==.
三、20.解:(1)原式=-8+4-2×+1=-8+4-1+1=-4.
(2)原式=()2--+2×()2×=.
21.解:由2a=3b,可得=.
设a=3k(k>0),则b=2k,
由勾股定理,得c===k,
∴sin B===,
cos B===,
tan B===.
22.解:(1)在Rt△ABE中,∵∠A=60°,∠ABE=90°,AB=6,tan A=,
∴∠E=30°,BE=AB·tan A=6×tan 60°=6 .
在Rt△CDE中,∵∠CDE=90°,CD=4,
∴CE=2CD=8.
∴BC=BE-CE=6 -8.
(2)在Rt△ABE中,sin A==,
∴可设BE=4x(x>0),则AE=5x.
由勾股定理可得AB=3x,
∴3x=6,解得x=2.
∴BE=8,AE=10.
易得tan E==,∴=,
解得DE=.
∴AD=AE-DE=10-=.
23.解:过点C作CD⊥AB于点D,设AD=x m,小明的行走速度是a m/s.
∵∠A=45°,CD⊥AB,
∴CD=AD=x m,AC=x m.
在Rt△BCD中,∵∠B=30°,
∴BC===2x(m).
∵小军的行走速度为 m/s,小明与小军同时到达山顶C处,
∴=,解得a=1.
答:小明的行走速度是1 m/s.
24.解:如图,在BC上取一点E,使AE=AC=,连接AE,过点E作EF⊥AB于点F,过点A作AD⊥CE于点D,
则∠AEC=∠C,DE=CD.
(第24题)
∵∠EAF=∠AEC-∠B,
∴∠EAF=∠C-∠B.
∵tan(∠C-∠B)=,
∴tan∠EAF=,即=,
设EF=6x,则AF=17x,由勾股定理得AF2+EF2=AE2,
∴(17x)2+(6x)2=()2,
∴x=(负值舍去),
∴EF=,AF=,
∴BF=AB-AF=5-=,
∴BE===2.
∵S△ABE=AB·EF=BE·AD,
∴AD===3,
∴CD=DE==2,
∴BC=BE+DE+CD=2+2+2=6.
25.解:如图,连接BC并延长BC交AD于点E,易知DE=1.6 m,则AE=AD-DE=0.6 m.
在Rt△ABE中,BE=≈≈1.88 (m),
在Rt△ACE中,CE=≈≈0.35 (m).
易知四边形MNBC是矩形,
∴MN=BC=BE-CE≈1.88-0.35≈1.5 (m).
答:小聪在地面的有效测温区间MN的长度约为1.5 m.
(第25题)
26.解:(1)∵AM⊥MN,CN⊥MN,
∴∠M=∠N=90°,
∴∠MAB+∠ABM=90°.
∵∠ABC=90°,
∴∠NBC+∠ABM=90°,
∴∠MAB=∠NBC,
∴△AMB∽△BNC,
∴==tan∠BAC=.
∵点B是线段MN的中点,
∴BM=BN,
∴在Rt△AMB中,tan∠BAM===.
(2)过点C作CD⊥AC交AP于点D,
过点D作DE⊥BP于点E.
∵tan∠BAC=,∠APB=∠BAC,
∴tan∠BAC==,
tan∠APB==.
设BC=x,则AB=2x,BP=4x,
∴CP=BP-BC=4x-x=3x.
易得∠BAC=∠ECD,
∴∠APB=∠ECD.
∵DE⊥BP,
∴CE=EP=CP=x.
∵∠BAC=∠ECD,∠B=∠CED=90°,
∴△ABC∽△CED,
∴===,
∴在Rt△ACD中,tan∠PAC==.
4
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
