期中复习测评 第1章勾股定理 2021-2022学年北师大版八年级数学上册(Word版含答案)
文档属性
| 名称 | 期中复习测评 第1章勾股定理 2021-2022学年北师大版八年级数学上册(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 295.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 00:00:00 | ||
图片预览


文档简介
2021-2022学年北师大版八年级数学上册《第1章勾股定理》期中复习测评(附答案)
一.选择题(共10小题,满分40分)
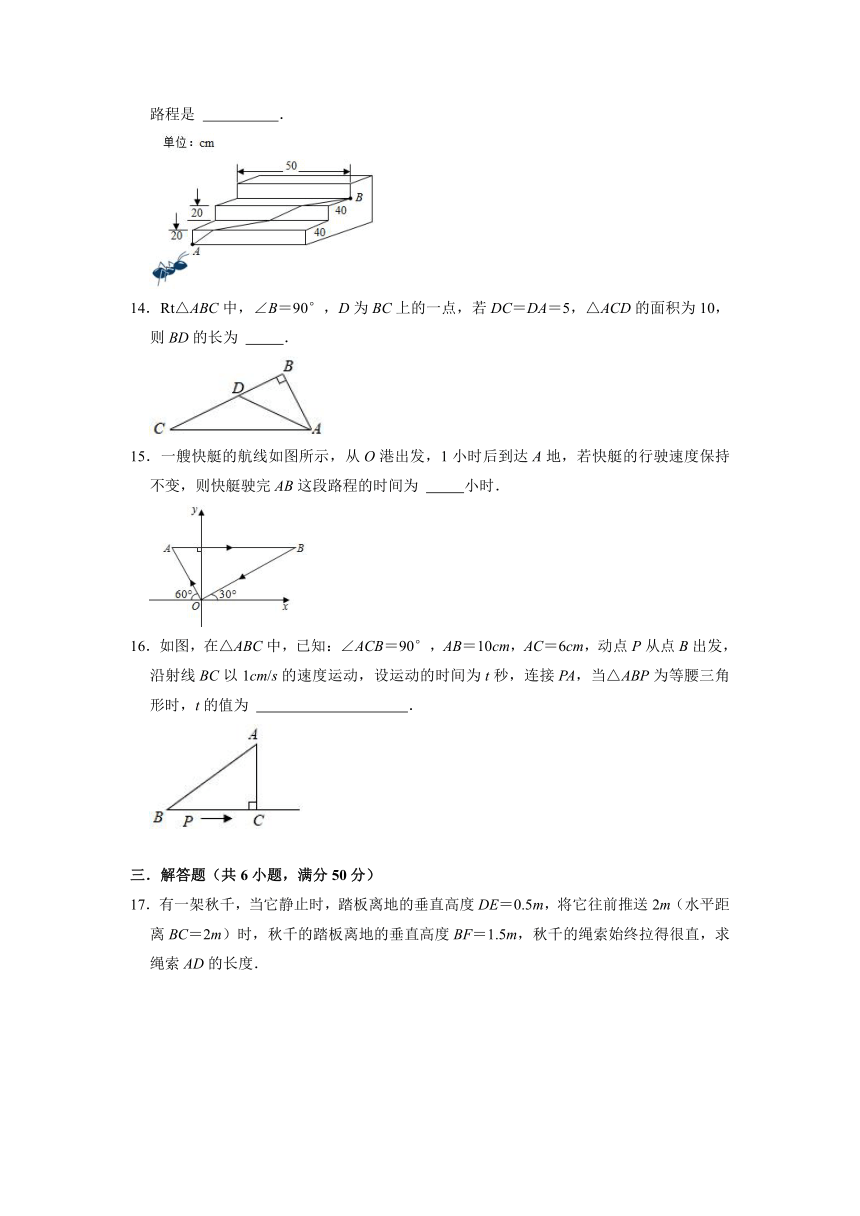
1.勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是( )
A.B.C.D.
2.如图,在Rt△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,若S1=3,S2=10,则S3=( )
A.5 B.7 C.13 D.15
3.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A.12cm2 B.18cm2 C.22cm2 D.36cm2
4.在Rt△ABC中,若∠C=90°,AC=3,BC=4,则点C到直线AB的距离为( )
A.3 B.4 C.5 D.2.4
5.如图,根据下列条件,不能判断△ABD是直角三角形的是( )
A.∠B=3∠D,∠BAD=8∠D B.AB=5,AD=12,BD=13
C.AC=BC=DC D.∠D=20°,∠B=70°
6.下列各组数中,不是勾股数的是( )
A.3,4,5 B.30,40,50 C.7,14,15 D.5,12,13
7.已知一直角三角形,三边的平方和为800cm2,则斜边长为( )
A.20cm B.40cm C.400cm D.不能确定
8.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,它至少要飞行( )
A.6米 B.8米 C.10米 D.14米
9.图1是第七届国际数学教育大会(ICME﹣7)会徽图案,它是由一串有公共顶点O的直角三角形(如图2)演化而成的.如果图2中的OA1=A1A2=A2A3= =A7A8=1,那么OA8的长为( )
A. B.4 C.3 D.2
10.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣9=(20﹣x)2 B.x2﹣92=(20﹣x)2
C.x2+9=(20﹣x)2 D.x2+92=(20﹣x)2
二.填空题(共6小题,满分30分)
11.如图,长方体的长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面从A爬行到B的最短路程是 .
12.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要 m.
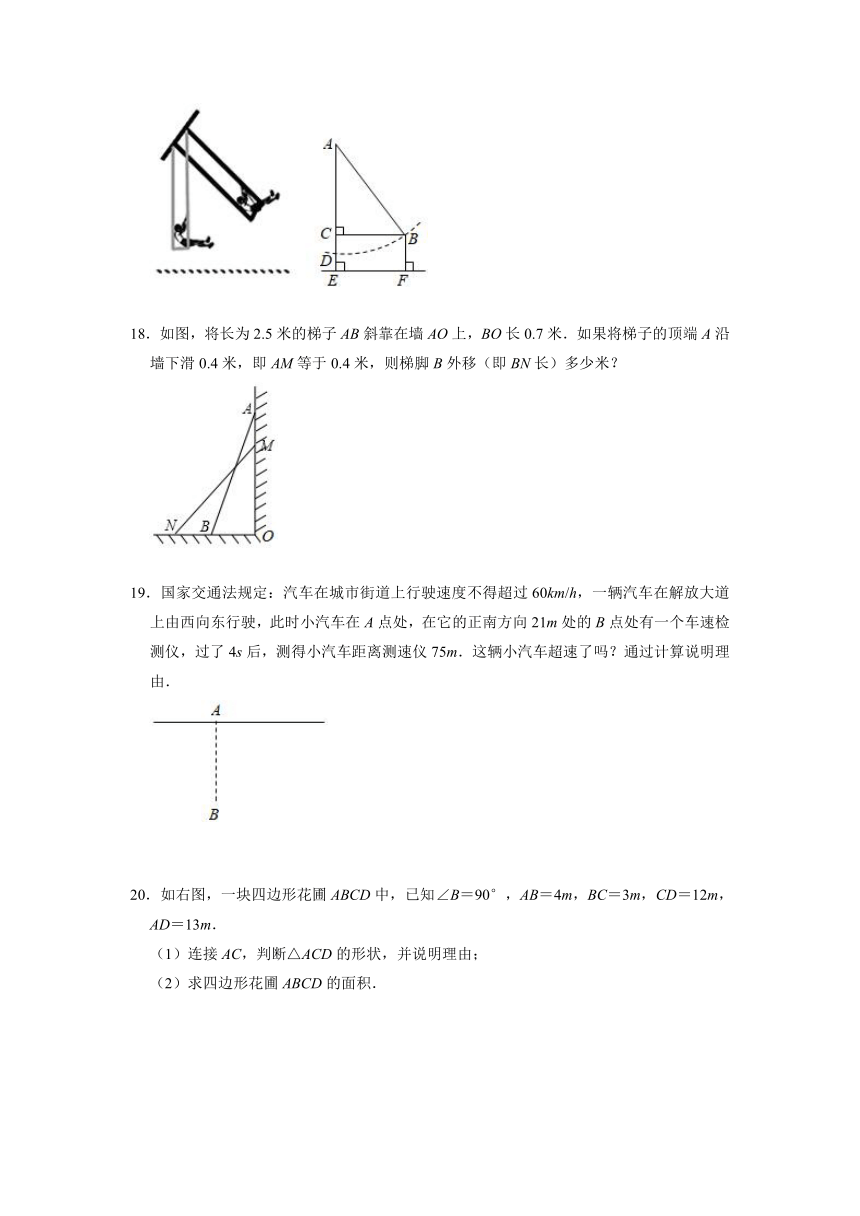
13.如图,台阶阶梯每一层高20cm,宽40cm,长50cm.一只蚂蚁从A点爬到B点,最短路程是 .
14.Rt△ABC中,∠B=90°,D为BC上的一点,若DC=DA=5,△ACD的面积为10,则BD的长为 .
15.一艘快艇的航线如图所示,从O港出发,1小时后到达A地,若快艇的行驶速度保持不变,则快艇驶完AB这段路程的时间为 小时.
16.如图,在△ABC中,已知:∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发,沿射线BC以1cm/s的速度运动,设运动的时间为t秒,连接PA,当△ABP为等腰三角形时,t的值为 .
三.解答题(共6小题,满分50分)
17.有一架秋千,当它静止时,踏板离地的垂直高度DE=0.5m,将它往前推送2m(水平距离BC=2m)时,秋千的踏板离地的垂直高度BF=1.5m,秋千的绳索始终拉得很直,求绳索AD的长度.
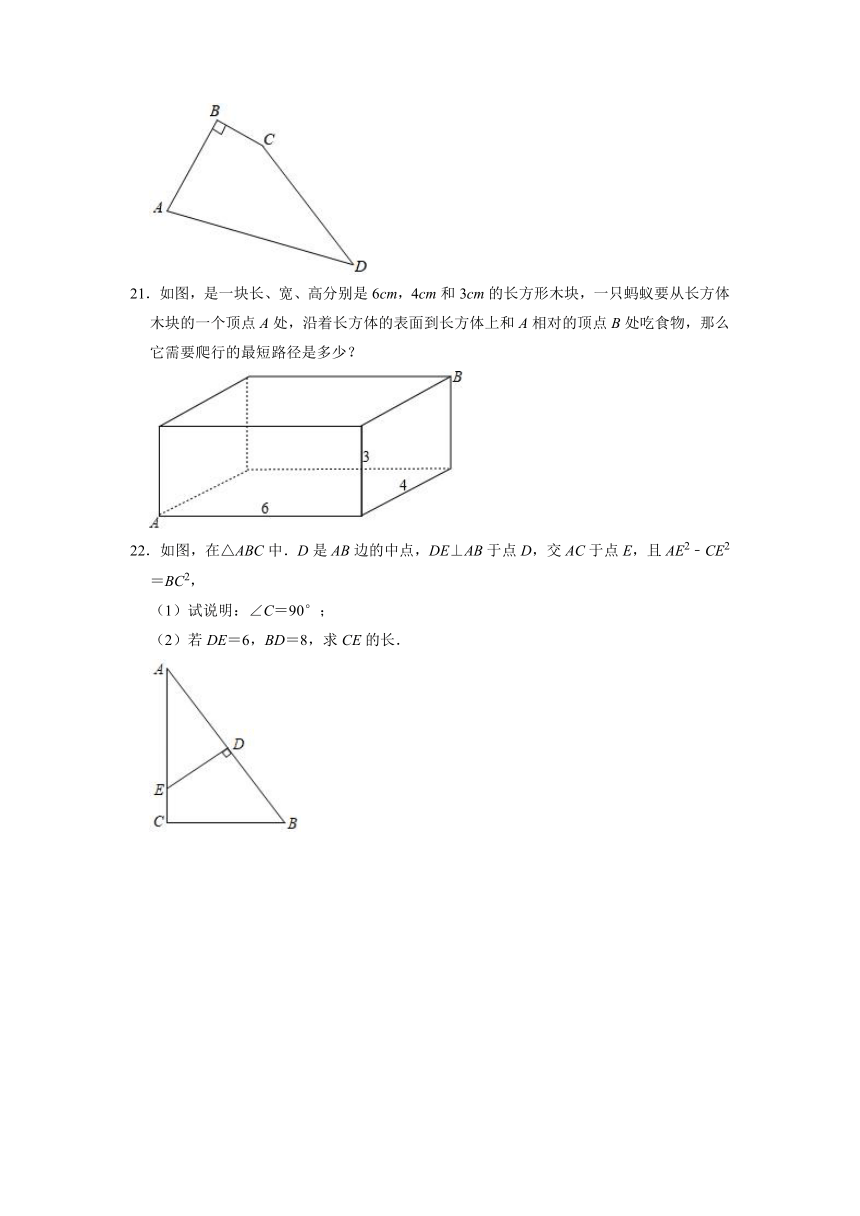
18.如图,将长为2.5米的梯子AB斜靠在墙AO上,BO长0.7米.如果将梯子的顶端A沿墙下滑0.4米,即AM等于0.4米,则梯脚B外移(即BN长)多少米?
19.国家交通法规定:汽车在城市街道上行驶速度不得超过60km/h,一辆汽车在解放大道上由西向东行驶,此时小汽车在A点处,在它的正南方向21m处的B点处有一个车速检测仪,过了4s后,测得小汽车距离测速仪75m.这辆小汽车超速了吗?通过计算说明理由.
20.如右图,一块四边形花圃ABCD中,已知∠B=90°,AB=4m,BC=3m,CD=12m,AD=13m.
(1)连接AC,判断△ACD的形状,并说明理由;
(2)求四边形花圃ABCD的面积.
21.如图,是一块长、宽、高分别是6cm,4cm和3cm的长方形木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径是多少?
22.如图,在△ABC中.D是AB边的中点,DE⊥AB于点D,交AC于点E,且AE2﹣CE2=BC2,
(1)试说明:∠C=90°;
(2)若DE=6,BD=8,求CE的长.
参考答案
一.选择题(共10小题,满分40分)
1.解:在A选项中,由图可知三个三角形的面积的和等于梯形的面积,
∴,
整理可得a2+b2=c2,
∴A选项可以证明勾股定理,
在B选项中,大正方形的面积等于四个三角形的面积加小正方形的面积,
∴,
整理得a2+b2=c2,
∴B选项可以证明勾股定理,
在C选项中,大正方形的面积等于四个三角形的面积加小正方形的面积,
∴,
整理得a2+b2=c2,
∴C选项可以说明勾股定理,
在D选项中,大正方形的面积等于四个矩形的面积的和,
∴(a+b)2=a2+2ab+b2,
以上公式为完全平方公式,
∴D选项不能说明勾股定理,
故选:D.
2.解:由勾股定理得,AC2+BC2=AB2,
∴AC2=10﹣3=7,
∴S3=7,
故选:B.
3.解:如图,连接BD,
∵∠A=90°,AB=3cm,AD=4cm,
∴BD===5(cm),
∵BC=13cm,CD=12cm,52+122=132,
∴BD2+CD2=CB2,
∴∠BDC=90°,
∴S△DBC=×DB×CD=×5×12=30(cm2),
S△ABD=×3×4=6(cm2),
∴四边形ABCD的面积为30+6=36(cm2),
故选:D.
4.解:作CD⊥AB于点D,如右图所示,
∵∠C=90°,AC=3,BC=4,
∴AB===5,
∵,
∴,
解得CD=2.4,
故选:D.
5.解:A、∵∠B=3∠D,∠BAD=8∠D,∴3∠D+∠D+8∠D=180°,解得∠D=15°,∴∠BAD=120°,∴△ABD不是直角三角形;
B、∵AB=5,AD=12,BD=13,52+122=132,∴△ABD是直角三角形;
C、由AC=BC=DC可得△ABD是直角三角形;
D、当∠D=20°,∠B=70°时,∠BAD=180°﹣20°﹣70°=90°,△ABD是直角三角形.
故选:A.
6.解:A、32+42=52,能构成直角三角形,是整数,故是勾股数,此选项不符合题意;
B、302+402=502,三边是整数,同时能构成直角三角形,故是勾股数,此选项不符合题意;
C、72+142≠152,不是勾股数,此选项符合题意;
D、52+122=132,是正整数,故是勾股数,此选项不符合题意.
故选:C.
7.解:设直角三角形的两条直角边分别为acm、bcm,斜边为ccm.
根据题意,得a2+b2+c2=800,
∵a2+b2=c2,
∴2c2=800,
∴c2=400,
∵c>0,
∴(cm).
故选:A.
8.解:两棵树的高度差为10﹣4=6m,间距为8m,
根据勾股定理可得:小鸟至少飞行的距离==10m.
故选:C.
9.解:∵OA1=1,
∴由勾股定理可得OA2==,
OA3==,
…,
∴OAn=,
∴OA8==2.
故选:D.
10.解:如图,设折断处离地面的高度为x尺,则AB=(20﹣x)尺,BC=9尺,
在Rt△ABC中,AC2+BC2=AB2,即x2+92=(20﹣x)2.
故选:D.
二.填空题(共6小题,满分30分)
11.解:如图1所示,
AB==(cm);
如图2所示,
AB==(cm);
如图3所示,
AB==(cm);
∵<<,
∴蚂蚁沿着表面从A爬行到B的最短路程是cm.
故答案为:cm.
12.解:由勾股定理得:
楼梯的水平宽度==12,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
∴地毯的长度至少是12+5=17(米).
故答案为:17.
13.解:如图所示,
∵它的每一级的长宽高为20cm,宽40cm,长50cm,
∴AB==130(cm).
答:蚂蚁沿着台阶面从点A爬行到点B的最短路程是130cm.
故答案为:130cm.
14.解:设BD=x,
在Rt△ABD中,由勾股定理得:AB==,
∵△ACD的面积为10,
∴×DC×AB=10,即×5×=10,
解得:x1=3,x2=﹣3(舍去),
∴BD的长为3,
故答案为:3.
15.解:∵∠AOD=60°,∠BOE=30°,
∴∠AOB=90°,
∴∠B=30°,
∴AB=2OA,
∴快艇驶完AB这段路程的时间为2小时,
故答案为:2.
16.解:在△ABC中,∠ACB=90°,
由勾股定理得:BC=cm,
∵△ABP为等腰三角形,
当AB=AP时,则BP=2BC=16cm,即t=16;
当BA=BP=10cm时,则t=10;
当PA=PB时,如图:设BP=PA=x,则PC=8﹣x,
在Rt△ACP中,由勾股定理得:
PC2+AC2=AP2,
∴(8﹣x)2+62=x2,
解得x=,
∴t=.
综上所述:t的值为16或10或.
故答案为:16或10或.
三.解答题(共6小题,满分50分)
17.解:在Rt△ACB中,
AC2+BC2=AB2,
设秋千的绳索长为xm,则AC=(x﹣1)m,
故x2=22+(x﹣1)2,
解得:x=2.5,
答:绳索AD的长度是2.5m.
18.解:由题意得:AB=2.5米,BO=0.7米,
在Rt△ABO中,由勾股定理得:
AO==2.4(米),
∴MO=AO﹣AM=2.4﹣0.4=2(米),
在Rt△MNO中,由勾股定理得:
NO==1.5(米),
∴NB=ON﹣OB=1.5﹣0.7=0.8(米),
∴梯脚B外移(即BN长)0.8米.
19.解:如图,AB=21,BC=75,
在Rt△ABC中,由勾股定理得:
AC=m,
72÷4=18米/秒=64.8千米/时>60千米/时,
∴超速了.
20.解:(1)连接AC,
因为∠B=90°,所以直角△ABC中,由勾股定理得:
AC2=AB2+BC2,
AC2=42+32,
AC2=25,
∴AC=5m,又CD=12m,AD=13m,
所以△ACD中,AC2+CD2=AD2,
所以△ACD是直角三角形;
(2)S四边形ABCD=AC CD+AB BC
S四边形ABCD=×5×12+×4×3
=30+6
=36(m2),
答:该花圃的面积为36m2.
21.解:如图1,当爬的长方形的长是(4+6)=10,宽是3时,AB==(cm).
如图2,当爬的长方形的长是(3+6)=9,宽是4时,AB==(cm).
如图3,爬的长方形的长是(3+4)=7时,宽是6时,AB==(cm).
∵>>,
∴它需要爬行的最短路径是cm.
22.解:(1)如图所示,连接BE,
∵D是AB边的中点,DE⊥AB于点D,
∴DE垂直平分AB,
∴AE=BE,
又∵AE2﹣CE2=BC2,
∴BE2﹣CE2=BC2,
∴△BCE是直角三角形,且∠C=90°;
(2)Rt△BDE中,BE===10,
∴AE=10,
设CE=x,则AC=10+x,而AB=2BD=16,
Rt△ABC中,BC2=AB2﹣AC2=162﹣(10+x)2,
Rt△BCE中,BC2=EB2﹣EC2=102﹣x2,
∴162﹣(10+x)2=102﹣x2,
解得x=2.8,
∴CE=2.8.
一.选择题(共10小题,满分40分)
1.勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是( )
A.B.C.D.
2.如图,在Rt△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,若S1=3,S2=10,则S3=( )
A.5 B.7 C.13 D.15
3.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A.12cm2 B.18cm2 C.22cm2 D.36cm2
4.在Rt△ABC中,若∠C=90°,AC=3,BC=4,则点C到直线AB的距离为( )
A.3 B.4 C.5 D.2.4
5.如图,根据下列条件,不能判断△ABD是直角三角形的是( )
A.∠B=3∠D,∠BAD=8∠D B.AB=5,AD=12,BD=13
C.AC=BC=DC D.∠D=20°,∠B=70°
6.下列各组数中,不是勾股数的是( )
A.3,4,5 B.30,40,50 C.7,14,15 D.5,12,13
7.已知一直角三角形,三边的平方和为800cm2,则斜边长为( )
A.20cm B.40cm C.400cm D.不能确定
8.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,它至少要飞行( )
A.6米 B.8米 C.10米 D.14米
9.图1是第七届国际数学教育大会(ICME﹣7)会徽图案,它是由一串有公共顶点O的直角三角形(如图2)演化而成的.如果图2中的OA1=A1A2=A2A3= =A7A8=1,那么OA8的长为( )
A. B.4 C.3 D.2
10.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣9=(20﹣x)2 B.x2﹣92=(20﹣x)2
C.x2+9=(20﹣x)2 D.x2+92=(20﹣x)2
二.填空题(共6小题,满分30分)
11.如图,长方体的长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面从A爬行到B的最短路程是 .
12.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要 m.
13.如图,台阶阶梯每一层高20cm,宽40cm,长50cm.一只蚂蚁从A点爬到B点,最短路程是 .
14.Rt△ABC中,∠B=90°,D为BC上的一点,若DC=DA=5,△ACD的面积为10,则BD的长为 .
15.一艘快艇的航线如图所示,从O港出发,1小时后到达A地,若快艇的行驶速度保持不变,则快艇驶完AB这段路程的时间为 小时.
16.如图,在△ABC中,已知:∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发,沿射线BC以1cm/s的速度运动,设运动的时间为t秒,连接PA,当△ABP为等腰三角形时,t的值为 .
三.解答题(共6小题,满分50分)
17.有一架秋千,当它静止时,踏板离地的垂直高度DE=0.5m,将它往前推送2m(水平距离BC=2m)时,秋千的踏板离地的垂直高度BF=1.5m,秋千的绳索始终拉得很直,求绳索AD的长度.
18.如图,将长为2.5米的梯子AB斜靠在墙AO上,BO长0.7米.如果将梯子的顶端A沿墙下滑0.4米,即AM等于0.4米,则梯脚B外移(即BN长)多少米?
19.国家交通法规定:汽车在城市街道上行驶速度不得超过60km/h,一辆汽车在解放大道上由西向东行驶,此时小汽车在A点处,在它的正南方向21m处的B点处有一个车速检测仪,过了4s后,测得小汽车距离测速仪75m.这辆小汽车超速了吗?通过计算说明理由.
20.如右图,一块四边形花圃ABCD中,已知∠B=90°,AB=4m,BC=3m,CD=12m,AD=13m.
(1)连接AC,判断△ACD的形状,并说明理由;
(2)求四边形花圃ABCD的面积.
21.如图,是一块长、宽、高分别是6cm,4cm和3cm的长方形木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径是多少?
22.如图,在△ABC中.D是AB边的中点,DE⊥AB于点D,交AC于点E,且AE2﹣CE2=BC2,
(1)试说明:∠C=90°;
(2)若DE=6,BD=8,求CE的长.
参考答案
一.选择题(共10小题,满分40分)
1.解:在A选项中,由图可知三个三角形的面积的和等于梯形的面积,
∴,
整理可得a2+b2=c2,
∴A选项可以证明勾股定理,
在B选项中,大正方形的面积等于四个三角形的面积加小正方形的面积,
∴,
整理得a2+b2=c2,
∴B选项可以证明勾股定理,
在C选项中,大正方形的面积等于四个三角形的面积加小正方形的面积,
∴,
整理得a2+b2=c2,
∴C选项可以说明勾股定理,
在D选项中,大正方形的面积等于四个矩形的面积的和,
∴(a+b)2=a2+2ab+b2,
以上公式为完全平方公式,
∴D选项不能说明勾股定理,
故选:D.
2.解:由勾股定理得,AC2+BC2=AB2,
∴AC2=10﹣3=7,
∴S3=7,
故选:B.
3.解:如图,连接BD,
∵∠A=90°,AB=3cm,AD=4cm,
∴BD===5(cm),
∵BC=13cm,CD=12cm,52+122=132,
∴BD2+CD2=CB2,
∴∠BDC=90°,
∴S△DBC=×DB×CD=×5×12=30(cm2),
S△ABD=×3×4=6(cm2),
∴四边形ABCD的面积为30+6=36(cm2),
故选:D.
4.解:作CD⊥AB于点D,如右图所示,
∵∠C=90°,AC=3,BC=4,
∴AB===5,
∵,
∴,
解得CD=2.4,
故选:D.
5.解:A、∵∠B=3∠D,∠BAD=8∠D,∴3∠D+∠D+8∠D=180°,解得∠D=15°,∴∠BAD=120°,∴△ABD不是直角三角形;
B、∵AB=5,AD=12,BD=13,52+122=132,∴△ABD是直角三角形;
C、由AC=BC=DC可得△ABD是直角三角形;
D、当∠D=20°,∠B=70°时,∠BAD=180°﹣20°﹣70°=90°,△ABD是直角三角形.
故选:A.
6.解:A、32+42=52,能构成直角三角形,是整数,故是勾股数,此选项不符合题意;
B、302+402=502,三边是整数,同时能构成直角三角形,故是勾股数,此选项不符合题意;
C、72+142≠152,不是勾股数,此选项符合题意;
D、52+122=132,是正整数,故是勾股数,此选项不符合题意.
故选:C.
7.解:设直角三角形的两条直角边分别为acm、bcm,斜边为ccm.
根据题意,得a2+b2+c2=800,
∵a2+b2=c2,
∴2c2=800,
∴c2=400,
∵c>0,
∴(cm).
故选:A.
8.解:两棵树的高度差为10﹣4=6m,间距为8m,
根据勾股定理可得:小鸟至少飞行的距离==10m.
故选:C.
9.解:∵OA1=1,
∴由勾股定理可得OA2==,
OA3==,
…,
∴OAn=,
∴OA8==2.
故选:D.
10.解:如图,设折断处离地面的高度为x尺,则AB=(20﹣x)尺,BC=9尺,
在Rt△ABC中,AC2+BC2=AB2,即x2+92=(20﹣x)2.
故选:D.
二.填空题(共6小题,满分30分)
11.解:如图1所示,
AB==(cm);
如图2所示,
AB==(cm);
如图3所示,
AB==(cm);
∵<<,
∴蚂蚁沿着表面从A爬行到B的最短路程是cm.
故答案为:cm.
12.解:由勾股定理得:
楼梯的水平宽度==12,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
∴地毯的长度至少是12+5=17(米).
故答案为:17.
13.解:如图所示,
∵它的每一级的长宽高为20cm,宽40cm,长50cm,
∴AB==130(cm).
答:蚂蚁沿着台阶面从点A爬行到点B的最短路程是130cm.
故答案为:130cm.
14.解:设BD=x,
在Rt△ABD中,由勾股定理得:AB==,
∵△ACD的面积为10,
∴×DC×AB=10,即×5×=10,
解得:x1=3,x2=﹣3(舍去),
∴BD的长为3,
故答案为:3.
15.解:∵∠AOD=60°,∠BOE=30°,
∴∠AOB=90°,
∴∠B=30°,
∴AB=2OA,
∴快艇驶完AB这段路程的时间为2小时,
故答案为:2.
16.解:在△ABC中,∠ACB=90°,
由勾股定理得:BC=cm,
∵△ABP为等腰三角形,
当AB=AP时,则BP=2BC=16cm,即t=16;
当BA=BP=10cm时,则t=10;
当PA=PB时,如图:设BP=PA=x,则PC=8﹣x,
在Rt△ACP中,由勾股定理得:
PC2+AC2=AP2,
∴(8﹣x)2+62=x2,
解得x=,
∴t=.
综上所述:t的值为16或10或.
故答案为:16或10或.
三.解答题(共6小题,满分50分)
17.解:在Rt△ACB中,
AC2+BC2=AB2,
设秋千的绳索长为xm,则AC=(x﹣1)m,
故x2=22+(x﹣1)2,
解得:x=2.5,
答:绳索AD的长度是2.5m.
18.解:由题意得:AB=2.5米,BO=0.7米,
在Rt△ABO中,由勾股定理得:
AO==2.4(米),
∴MO=AO﹣AM=2.4﹣0.4=2(米),
在Rt△MNO中,由勾股定理得:
NO==1.5(米),
∴NB=ON﹣OB=1.5﹣0.7=0.8(米),
∴梯脚B外移(即BN长)0.8米.
19.解:如图,AB=21,BC=75,
在Rt△ABC中,由勾股定理得:
AC=m,
72÷4=18米/秒=64.8千米/时>60千米/时,
∴超速了.
20.解:(1)连接AC,
因为∠B=90°,所以直角△ABC中,由勾股定理得:
AC2=AB2+BC2,
AC2=42+32,
AC2=25,
∴AC=5m,又CD=12m,AD=13m,
所以△ACD中,AC2+CD2=AD2,
所以△ACD是直角三角形;
(2)S四边形ABCD=AC CD+AB BC
S四边形ABCD=×5×12+×4×3
=30+6
=36(m2),
答:该花圃的面积为36m2.
21.解:如图1,当爬的长方形的长是(4+6)=10,宽是3时,AB==(cm).
如图2,当爬的长方形的长是(3+6)=9,宽是4时,AB==(cm).
如图3,爬的长方形的长是(3+4)=7时,宽是6时,AB==(cm).
∵>>,
∴它需要爬行的最短路径是cm.
22.解:(1)如图所示,连接BE,
∵D是AB边的中点,DE⊥AB于点D,
∴DE垂直平分AB,
∴AE=BE,
又∵AE2﹣CE2=BC2,
∴BE2﹣CE2=BC2,
∴△BCE是直角三角形,且∠C=90°;
(2)Rt△BDE中,BE===10,
∴AE=10,
设CE=x,则AC=10+x,而AB=2BD=16,
Rt△ABC中,BC2=AB2﹣AC2=162﹣(10+x)2,
Rt△BCE中,BC2=EB2﹣EC2=102﹣x2,
∴162﹣(10+x)2=102﹣x2,
解得x=2.8,
∴CE=2.8.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
