2021-2022学年度北师大版八年级数学上册 4 一次函数的应用(3课时)教案
文档属性
| 名称 | 2021-2022学年度北师大版八年级数学上册 4 一次函数的应用(3课时)教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 389.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 00:00:00 | ||
图片预览



文档简介
4 一次函数的应用
第1课时 借助一次函数表达式解决一些简单问题
一、基本目标
会用待定系数法求一次函数的表达式,并能运用一次函数知识解决简单的实际问题.
二、重难点目标
【教学重点】
会利用待定系数法确定一次函数的表达式.
【教学难点】
通过求一次函数的表达式来解决简单的实际问题.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P89的内容,完成下面练习.
【3 min反馈】
物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)的关系如图所示.
(1)写出v与t之间的关系式;
(2)下滑3秒时物体的速度是多少?
解:(1)v=t.
(2)当t=3时,v=×3=.所以下滑3秒时物体的速度是 m/s.
环节2 合作探究,解决问题
活动1 小组讨论(师生对学)
【例1】求正比例函数y=(m-4)xm2-15的表达式.
【互动探索】(引发学生思考)本题是利用正比例函数的定义来确定表达式的,即自变量的指数为1,系数不为0,这种类型简称为定义式.
【解答】由正比例函数的定义知m2-15=1且m-4≠0,∴m=-4,∴y=-8x.
【互动总结】(学生总结,老师点评)利用正比例函数的定义确定表达式:自变量的指数为1,系数不为0.
【例2】已知一次函数的图象经过(0,5)、(2,-5)两点,求一次函数的表达式.
【互动探索】(引发学生思考)先设一次函数的表达式为y=kx+b,因为它的图象经过(0,5)、(2,-5)两点,所以当x=0时,y=5;当x=2时,y=-5.由此可以得到两个关于k、b的方程,通过解方程即可求出待定系数k和b的值,再代回原设即可.
【解答】设一次函数的表达式为y=kx+b.
根据题意,得解得
∴一次函数的表达式为y=-5x+5.
【互动总结】(学生总结,老师点评)“两点式”是求一次函数表达式的基本题型.二次函数y=kx+b中有两个待定系数k、b,因而需要知道两个点的坐标才能确定函数的关系式.
活动2 巩固练习(学生独学)
1.已知正比例函数y=kx,当x=-3时,y=6.那么该正比例函数应为( B )
A.y=x B.y=-2x
C.y=-x D.y=2x
2.一次函数的图象经过点(2,1)和(-1,-3),则它的表达式为( D )
A.y=x- B.y=x-
C.y=x+ D.y=x-
3.已知y=kx-4,当x=-2时,y=0,则k=-2.
活动3 拓展延伸(学生对学)
【例3】某商店售货时,在进价的基础上加一定利润,其数量x与售价y的关系如下表所示,请你根据表中所提供的信息,列出售价y(元)与数量x(千克)的函数关系式,并求出当数量是2.5千克时的售价.
数量x/千克 售价y/元
1 8+0.4
2 16+0.8
3 24+1.2
4 32+1.6
5 40+2.0
… …
【互动探索】从图表中可以看出售价由8+0.4依次向下扩大到2倍、3倍……从中怎样得到函数关系式?
【解答】由表中信息,得y=(8+0.4)x=8.4x,即售价y与数量x的函数关系式为y=8.4x.当x=2.5时,y=8.4×2.5=21.所以数量是2.5千克时的售价是21元.
【互动总结】(学生总结,老师点评)解此类题要根据所给的条件建立数学模型,得出变化关系,并求出函数的表达式,根据函数的表达式作答.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
确定一次函数表达式
请完成本课时对应练习!
第2课时 借助单个一次函数图象解决简单实际问题
一、基本目标
通过运用一次函数知识解决实际问题,及其与一元一次方程的关系,进一步加深理解并掌握所学知识.
二、重难点目标
【教学重点】
掌握单个一次函数图象的应用.
【教学难点】
了解一次函数与一元一次方程的关系.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P91~P92的内容,完成下面练习.
【3 min反馈】
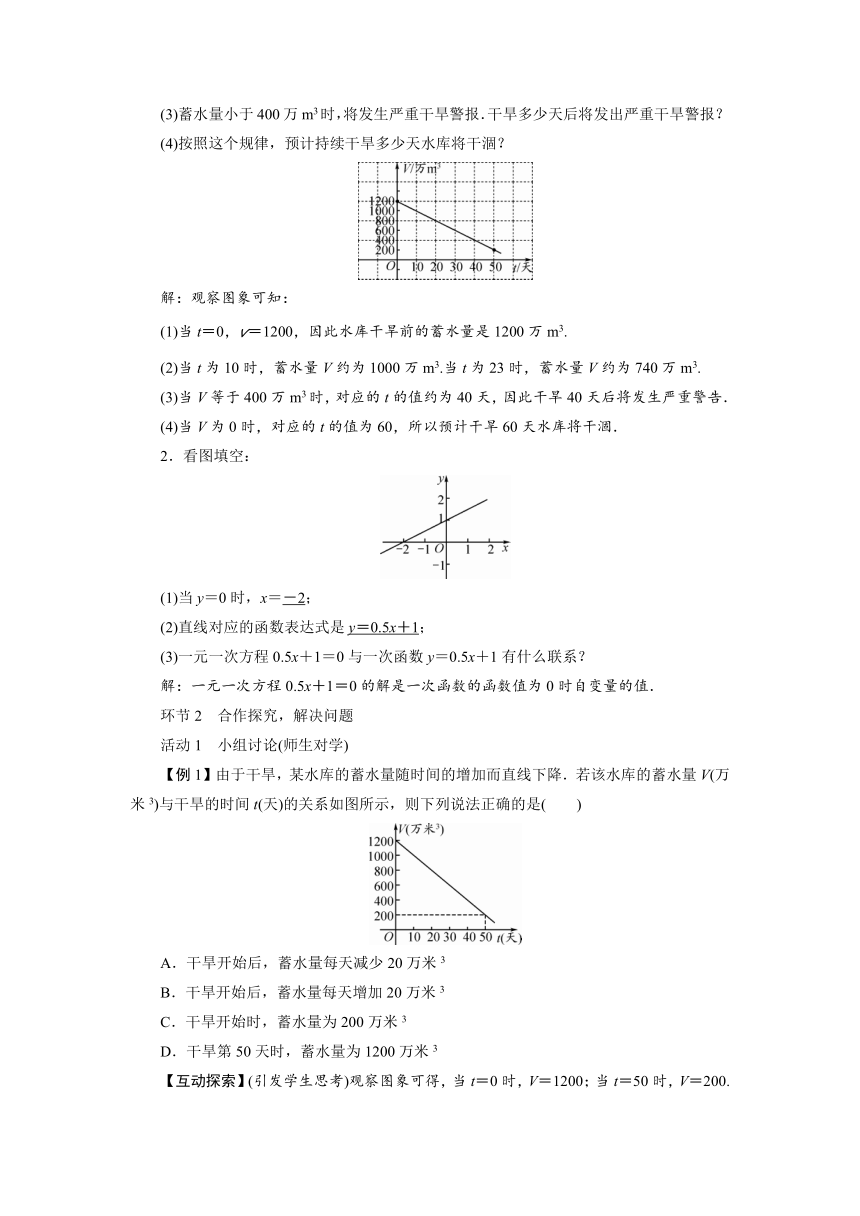
1.由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.蓄水量V(万m3)与干旱持续时间t(天)的关系如下图所示,回答下列问题:
(1)水库干旱前的蓄水量是多少?
(2)干旱持续10天后,蓄水量为多少?连续干旱23天后呢?
(3)蓄水量小于400万m3时,将发生严重干旱警报.干旱多少天后将发出严重干旱警报?
(4)按照这个规律,预计持续干旱多少天水库将干涸?
解:观察图象可知:
(1)当t=0,v=1200,因此水库干旱前的蓄水量是1200万m3.
(2)当t为10时,蓄水量V约为1000万m3.当t为23时,蓄水量V约为740万m3.
(3)当V等于400万m3时,对应的t的值约为40天,因此干旱40天后将发生严重警告.
(4)当V为0时,对应的t的值为60,所以预计干旱60天水库将干涸.
2.看图填空:
(1)当y=0时,x=-2;
(2)直线对应的函数表达式是y=0.5x+1;
(3)一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
解:一元一次方程0.5x+1=0的解是一次函数的函数值为0时自变量的值.
环节2 合作探究,解决问题
活动1 小组讨论(师生对学)
【例1】由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( )
A.干旱开始后,蓄水量每天减少20万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱第50天时,蓄水量为1200万米3
【互动探索】(引发学生思考)观察图象可得,当t=0时,V=1200;当t=50时,V=200.所以从干旱开始到第50天,蓄水量减少了1200-200=1000(万米3),则每天减少1000÷50=20(万米3).
【答案】A
【互动总结】(学生总结,老师点评)要认真观察图象,结合题意,弄清各点所表示的意义.
活动2 巩固练习(学生独学)
1.某公司销售人员的个人月收入与其每月的销售量成一次函数关系,图象如图所示,则此销售人员的销售量为3千件时的月收入是1400元.
2.一次函数y=kx+b的图象与y轴相交于点(0,-3),且方程kx+b=0的解为x=2,试求这个一次函数的表达式.
解:由题意可知,b=-3,且函数图象与x轴交点坐标为(2,0),所以可得2k-3=0,解得k=,故一次函数表达式为y=x-3.
活动3 拓展延伸(学生对学)
【例2】一次函数y=kx+b(k、b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为( )
A.x=-1 B.x=2
C.x=0 D.x=3
【互动探索】首先由函数经过点(0,1)可得b=1,再将点(2,3)代入y=kx+1,可求出k的值为1,从而可得出一次函数的表达式为y=x+1,再求出方程x+1=0的解为x=-1.
【答案】A
【互动总结】(学生总结,老师点评)此题主要考查了一次函数与一元一次方程的关系,关键是正确利用待定系数法求出一次函数的关系式.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
一次函数的应用
请完成本课时对应练习!
第3课时 借助两个一次函数图象解决简单实际问题
一、基本目标
1.会应用一次函数表达式与图象之间的相互关系,处理一些较为复杂的问题,领会数形结合的思想.
2.经历对实际问题建立数学模型的过程,体验数形结合的作用和一次函数模型的价值.
二、重难点目标
【教学重点】
掌握两个一次函数图象的应用.
【教学难点】
能利用函数图象解决实际问题.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P93~P95的内容,完成下面练习.
【3 min反馈】
1.如图,图象l甲、l乙分别表示甲、乙两名运动员在校运动会800米比赛中所跑的路程s(米)与时间t(分)之间的关系,则他们跑的速度关系是( A )
A.甲跑的速度比乙跑的速度快
B.乙跑的速度比甲跑的速度快
C.甲、乙两人跑的速度一样快
D.图中提供的信息不足,无法判断
2.如图,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量( D )
A.小于3 t B.大于3 t
C.小于4 t D.大于4 t
环节2 合作探究,解决问题
活动1 小组讨论(师生对学)
【例1】自来水公司有甲、乙两个蓄水池,现将甲池中的水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(小时)之间的函数图象如图所示,结合图象回答下列问题.
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数表达式;
(2)求注入多长时间后甲、乙两个蓄水池的深度相同;
(3)3小时后,若将乙蓄水池中的水按原速全部注入甲蓄水池,又需多长时间?
【互动探索】(引发学生思考)(1)根据图象确定点的坐标,再运用待定系数法确定函数表达式;(2)根据甲、乙两个蓄水池水的深度相同,可以得到一个一元一次方程,解此方程可得注水时间;(3)由图可知,乙蓄水池的水深为4米,乙蓄水池水上升的速度为1米/小时,由此求得答案即可.
【解答】(1)设它们的函数关系式为y=kx+b.根据甲的函数图象可知,当x=0,y=2;当x=3时,y=0,将它们分别代入所设函数关系式y=kx+b中,得k=-,b=2,所以甲蓄水池中水的深度y与注水时间x之间的函数关系式为y=-x+2.同理可得,乙蓄水池中水的深度y与注水时间x之间的函数关系式为y=x+1.
(2)由题意,得-x+2=x+1,解得x=.故当注水小时后,甲、乙两个蓄水池水的深度相同.
(3)4÷(3÷3)=4(小时).所以若将乙蓄水池中的水按原速全部注入甲蓄水池,又需要4小时.
【互动总结】(学生总结,老师点评)本题首先根据图象确定一次函数的表达式.然后结合方程思想解题.
活动2 巩固练习(学生独学)
1.如图,OA、BA分别表示甲、乙两名学生运动的一次函数,图中s和t分别表示运动路程和时间,根据图象判断快者比慢者每秒快( B )
A.1 m B.1.5 m
C.2 m D.2.5 m
2.某公司为用户提供网费的两种收费方式如下表:
收费标准/方式 基础费用(单位:元/月) 单价(单位:元/分)
A 0 0.1
B 20 0.05
若设用户上网的时间为x分钟,A、B两种收费方式的费用分别为yA(元)、yB(元),它们的函数图象如图所示,则当上网时间多于400分钟时,选择B种方式省钱.(填“A”或“B”)
3.王教授和孙子小强经常一起爬山.有一天,小强让爷爷先走,然后追赶爷爷,图中的两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时).
(1)小强让爷爷先走了多少米?
(2)山顶离山脚的距离为多少米?谁先爬上了山顶?
(3)小强经过多长时间追上了爷爷?
解:(1)由图象可知,小强让爷爷先走了60米.
(2)由y轴纵坐标可知,山顶离山脚的距离为300米,由图象可知小强先爬上了山顶.
(3)根据函数图象可得,小强的速度为30米/分,240米处追上爷爷,两条线段的交点的横坐标即为相遇时的时间,即为240÷30=8(分钟).
活动3 拓展延伸(学生对学)
【例2】已知一次函数y=x+a和y=-x+b的图象都经过点A(-4,0),且与y轴分别交于B、C两点,求△ABC的面积.
【互动探索】充分利用数形结合的方法,求出点B、C的坐标,求得BC的长,进而求出面积.
【解答】∵y=x+a与y=-x+b的图象都过点A(-4,0),∴×(-4)+a=0,-×(-4)+b=0.∴a=6,b=-2.∴两个一次函数分别是y=x+6和y=-x-2.y=x+6与y轴交于点B,则B(0,6);y=-x-2与y轴交于点C,则C(0,-2).∴S△ABC=BC·AO=×(6+2)×4=16.
【互动总结】(学生总结,老师点评)解此类题要先求得顶点的坐标,即两个一次函数的交点和它们分别与x轴、y轴交点的坐标.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
两个一次函数的应用
请完成本课时对应练习!
第1课时 借助一次函数表达式解决一些简单问题
一、基本目标
会用待定系数法求一次函数的表达式,并能运用一次函数知识解决简单的实际问题.
二、重难点目标
【教学重点】
会利用待定系数法确定一次函数的表达式.
【教学难点】
通过求一次函数的表达式来解决简单的实际问题.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P89的内容,完成下面练习.
【3 min反馈】
物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)的关系如图所示.
(1)写出v与t之间的关系式;
(2)下滑3秒时物体的速度是多少?
解:(1)v=t.
(2)当t=3时,v=×3=.所以下滑3秒时物体的速度是 m/s.
环节2 合作探究,解决问题
活动1 小组讨论(师生对学)
【例1】求正比例函数y=(m-4)xm2-15的表达式.
【互动探索】(引发学生思考)本题是利用正比例函数的定义来确定表达式的,即自变量的指数为1,系数不为0,这种类型简称为定义式.
【解答】由正比例函数的定义知m2-15=1且m-4≠0,∴m=-4,∴y=-8x.
【互动总结】(学生总结,老师点评)利用正比例函数的定义确定表达式:自变量的指数为1,系数不为0.
【例2】已知一次函数的图象经过(0,5)、(2,-5)两点,求一次函数的表达式.
【互动探索】(引发学生思考)先设一次函数的表达式为y=kx+b,因为它的图象经过(0,5)、(2,-5)两点,所以当x=0时,y=5;当x=2时,y=-5.由此可以得到两个关于k、b的方程,通过解方程即可求出待定系数k和b的值,再代回原设即可.
【解答】设一次函数的表达式为y=kx+b.
根据题意,得解得
∴一次函数的表达式为y=-5x+5.
【互动总结】(学生总结,老师点评)“两点式”是求一次函数表达式的基本题型.二次函数y=kx+b中有两个待定系数k、b,因而需要知道两个点的坐标才能确定函数的关系式.
活动2 巩固练习(学生独学)
1.已知正比例函数y=kx,当x=-3时,y=6.那么该正比例函数应为( B )
A.y=x B.y=-2x
C.y=-x D.y=2x
2.一次函数的图象经过点(2,1)和(-1,-3),则它的表达式为( D )
A.y=x- B.y=x-
C.y=x+ D.y=x-
3.已知y=kx-4,当x=-2时,y=0,则k=-2.
活动3 拓展延伸(学生对学)
【例3】某商店售货时,在进价的基础上加一定利润,其数量x与售价y的关系如下表所示,请你根据表中所提供的信息,列出售价y(元)与数量x(千克)的函数关系式,并求出当数量是2.5千克时的售价.
数量x/千克 售价y/元
1 8+0.4
2 16+0.8
3 24+1.2
4 32+1.6
5 40+2.0
… …
【互动探索】从图表中可以看出售价由8+0.4依次向下扩大到2倍、3倍……从中怎样得到函数关系式?
【解答】由表中信息,得y=(8+0.4)x=8.4x,即售价y与数量x的函数关系式为y=8.4x.当x=2.5时,y=8.4×2.5=21.所以数量是2.5千克时的售价是21元.
【互动总结】(学生总结,老师点评)解此类题要根据所给的条件建立数学模型,得出变化关系,并求出函数的表达式,根据函数的表达式作答.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
确定一次函数表达式
请完成本课时对应练习!
第2课时 借助单个一次函数图象解决简单实际问题
一、基本目标
通过运用一次函数知识解决实际问题,及其与一元一次方程的关系,进一步加深理解并掌握所学知识.
二、重难点目标
【教学重点】
掌握单个一次函数图象的应用.
【教学难点】
了解一次函数与一元一次方程的关系.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P91~P92的内容,完成下面练习.
【3 min反馈】
1.由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.蓄水量V(万m3)与干旱持续时间t(天)的关系如下图所示,回答下列问题:
(1)水库干旱前的蓄水量是多少?
(2)干旱持续10天后,蓄水量为多少?连续干旱23天后呢?
(3)蓄水量小于400万m3时,将发生严重干旱警报.干旱多少天后将发出严重干旱警报?
(4)按照这个规律,预计持续干旱多少天水库将干涸?
解:观察图象可知:
(1)当t=0,v=1200,因此水库干旱前的蓄水量是1200万m3.
(2)当t为10时,蓄水量V约为1000万m3.当t为23时,蓄水量V约为740万m3.
(3)当V等于400万m3时,对应的t的值约为40天,因此干旱40天后将发生严重警告.
(4)当V为0时,对应的t的值为60,所以预计干旱60天水库将干涸.
2.看图填空:
(1)当y=0时,x=-2;
(2)直线对应的函数表达式是y=0.5x+1;
(3)一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
解:一元一次方程0.5x+1=0的解是一次函数的函数值为0时自变量的值.
环节2 合作探究,解决问题
活动1 小组讨论(师生对学)
【例1】由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( )
A.干旱开始后,蓄水量每天减少20万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱第50天时,蓄水量为1200万米3
【互动探索】(引发学生思考)观察图象可得,当t=0时,V=1200;当t=50时,V=200.所以从干旱开始到第50天,蓄水量减少了1200-200=1000(万米3),则每天减少1000÷50=20(万米3).
【答案】A
【互动总结】(学生总结,老师点评)要认真观察图象,结合题意,弄清各点所表示的意义.
活动2 巩固练习(学生独学)
1.某公司销售人员的个人月收入与其每月的销售量成一次函数关系,图象如图所示,则此销售人员的销售量为3千件时的月收入是1400元.
2.一次函数y=kx+b的图象与y轴相交于点(0,-3),且方程kx+b=0的解为x=2,试求这个一次函数的表达式.
解:由题意可知,b=-3,且函数图象与x轴交点坐标为(2,0),所以可得2k-3=0,解得k=,故一次函数表达式为y=x-3.
活动3 拓展延伸(学生对学)
【例2】一次函数y=kx+b(k、b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为( )
A.x=-1 B.x=2
C.x=0 D.x=3
【互动探索】首先由函数经过点(0,1)可得b=1,再将点(2,3)代入y=kx+1,可求出k的值为1,从而可得出一次函数的表达式为y=x+1,再求出方程x+1=0的解为x=-1.
【答案】A
【互动总结】(学生总结,老师点评)此题主要考查了一次函数与一元一次方程的关系,关键是正确利用待定系数法求出一次函数的关系式.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
一次函数的应用
请完成本课时对应练习!
第3课时 借助两个一次函数图象解决简单实际问题
一、基本目标
1.会应用一次函数表达式与图象之间的相互关系,处理一些较为复杂的问题,领会数形结合的思想.
2.经历对实际问题建立数学模型的过程,体验数形结合的作用和一次函数模型的价值.
二、重难点目标
【教学重点】
掌握两个一次函数图象的应用.
【教学难点】
能利用函数图象解决实际问题.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P93~P95的内容,完成下面练习.
【3 min反馈】
1.如图,图象l甲、l乙分别表示甲、乙两名运动员在校运动会800米比赛中所跑的路程s(米)与时间t(分)之间的关系,则他们跑的速度关系是( A )
A.甲跑的速度比乙跑的速度快
B.乙跑的速度比甲跑的速度快
C.甲、乙两人跑的速度一样快
D.图中提供的信息不足,无法判断
2.如图,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量( D )
A.小于3 t B.大于3 t
C.小于4 t D.大于4 t
环节2 合作探究,解决问题
活动1 小组讨论(师生对学)
【例1】自来水公司有甲、乙两个蓄水池,现将甲池中的水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(小时)之间的函数图象如图所示,结合图象回答下列问题.
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数表达式;
(2)求注入多长时间后甲、乙两个蓄水池的深度相同;
(3)3小时后,若将乙蓄水池中的水按原速全部注入甲蓄水池,又需多长时间?
【互动探索】(引发学生思考)(1)根据图象确定点的坐标,再运用待定系数法确定函数表达式;(2)根据甲、乙两个蓄水池水的深度相同,可以得到一个一元一次方程,解此方程可得注水时间;(3)由图可知,乙蓄水池的水深为4米,乙蓄水池水上升的速度为1米/小时,由此求得答案即可.
【解答】(1)设它们的函数关系式为y=kx+b.根据甲的函数图象可知,当x=0,y=2;当x=3时,y=0,将它们分别代入所设函数关系式y=kx+b中,得k=-,b=2,所以甲蓄水池中水的深度y与注水时间x之间的函数关系式为y=-x+2.同理可得,乙蓄水池中水的深度y与注水时间x之间的函数关系式为y=x+1.
(2)由题意,得-x+2=x+1,解得x=.故当注水小时后,甲、乙两个蓄水池水的深度相同.
(3)4÷(3÷3)=4(小时).所以若将乙蓄水池中的水按原速全部注入甲蓄水池,又需要4小时.
【互动总结】(学生总结,老师点评)本题首先根据图象确定一次函数的表达式.然后结合方程思想解题.
活动2 巩固练习(学生独学)
1.如图,OA、BA分别表示甲、乙两名学生运动的一次函数,图中s和t分别表示运动路程和时间,根据图象判断快者比慢者每秒快( B )
A.1 m B.1.5 m
C.2 m D.2.5 m
2.某公司为用户提供网费的两种收费方式如下表:
收费标准/方式 基础费用(单位:元/月) 单价(单位:元/分)
A 0 0.1
B 20 0.05
若设用户上网的时间为x分钟,A、B两种收费方式的费用分别为yA(元)、yB(元),它们的函数图象如图所示,则当上网时间多于400分钟时,选择B种方式省钱.(填“A”或“B”)
3.王教授和孙子小强经常一起爬山.有一天,小强让爷爷先走,然后追赶爷爷,图中的两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时).
(1)小强让爷爷先走了多少米?
(2)山顶离山脚的距离为多少米?谁先爬上了山顶?
(3)小强经过多长时间追上了爷爷?
解:(1)由图象可知,小强让爷爷先走了60米.
(2)由y轴纵坐标可知,山顶离山脚的距离为300米,由图象可知小强先爬上了山顶.
(3)根据函数图象可得,小强的速度为30米/分,240米处追上爷爷,两条线段的交点的横坐标即为相遇时的时间,即为240÷30=8(分钟).
活动3 拓展延伸(学生对学)
【例2】已知一次函数y=x+a和y=-x+b的图象都经过点A(-4,0),且与y轴分别交于B、C两点,求△ABC的面积.
【互动探索】充分利用数形结合的方法,求出点B、C的坐标,求得BC的长,进而求出面积.
【解答】∵y=x+a与y=-x+b的图象都过点A(-4,0),∴×(-4)+a=0,-×(-4)+b=0.∴a=6,b=-2.∴两个一次函数分别是y=x+6和y=-x-2.y=x+6与y轴交于点B,则B(0,6);y=-x-2与y轴交于点C,则C(0,-2).∴S△ABC=BC·AO=×(6+2)×4=16.
【互动总结】(学生总结,老师点评)解此类题要先求得顶点的坐标,即两个一次函数的交点和它们分别与x轴、y轴交点的坐标.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
两个一次函数的应用
请完成本课时对应练习!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
