青岛版 数学六年级下册 第二单元 圆柱圆锥体积练习(课件)(共15张PPT)
文档属性
| 名称 | 青岛版 数学六年级下册 第二单元 圆柱圆锥体积练习(课件)(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-03 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
圆柱、圆锥体积练习
梳理总结 提升认识
分层练习 巩固提高
问题回顾 再现新知
一 、问题回顾 再现新知
圆柱体积=底面积×高
V圆柱=Sh
圆锥体积= 底面积×高×
V圆锥= Sh
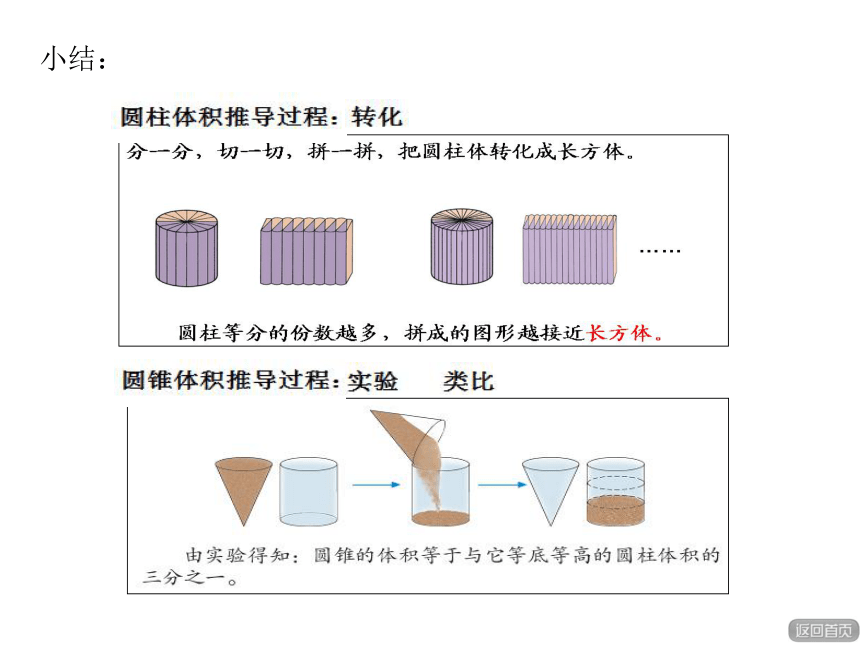
圆柱体积推导演示
圆锥体积推导演示
小结:
基本练习,巩固新知
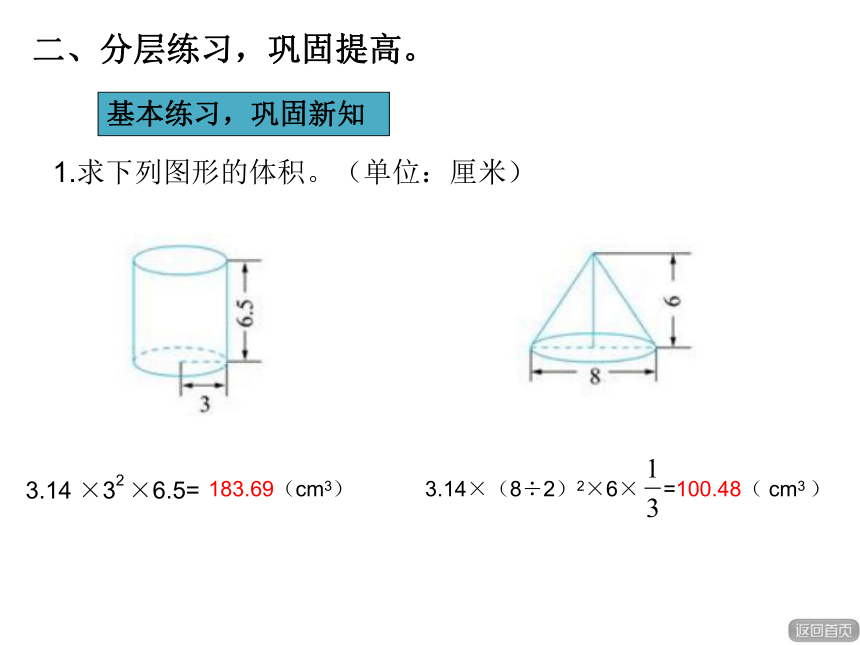
1.求下列图形的体积。(单位:厘米)
3.14 ×32 ×6.5=
3.14×(8÷2)2×6× =
183.69(cm3)
100.48( cm3 )
二、分层练习,巩固提高。
①圆柱体积是圆锥体积的3倍。( )
②一个圆锥体,底面积不变,高扩大6倍,体积也扩大6倍。( )
③把一个圆柱削成一个最大的圆锥,削去部分的体积是原体积的2/3。( )
④一个圆锥的体积是75立方米,底面积是25平方米,则它的高是3米。( )
2.判断题.
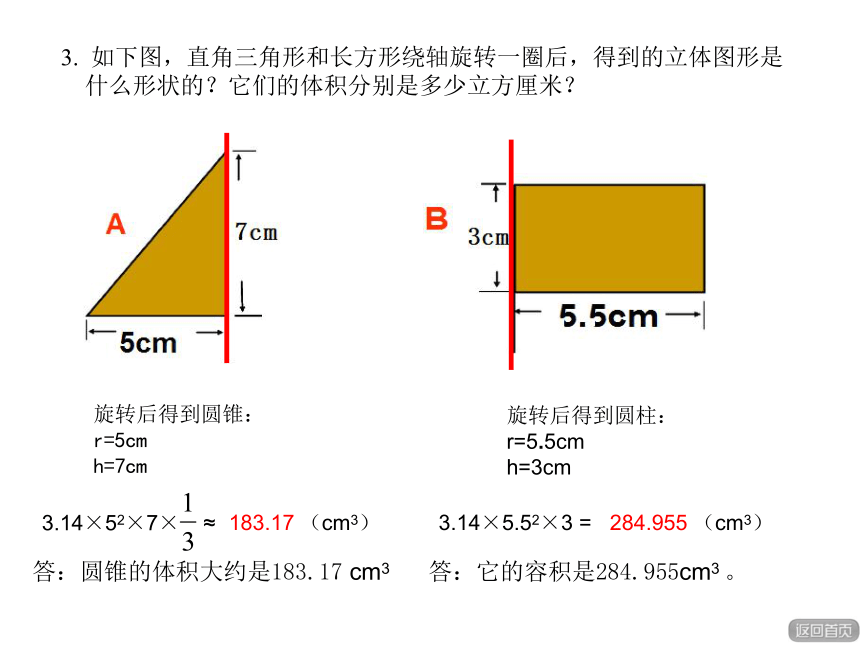
3. 如下图,直角三角形和长方形绕轴旋转一圈后,得到的立体图形是
什么形状的?它们的体积分别是多少立方厘米?
旋转后得到圆锥:r=5cm
h=7cm
3.14×52×7× ≈
183.17 (cm3)
旋转后得到圆柱:r=5.5cm
h=3cm
3.14×5.52×3 =
284.955 (cm3)
答:圆锥的体积大约是183.17 cm3
答:它的容积是284.955cm3 。
2.1米
10米
6米
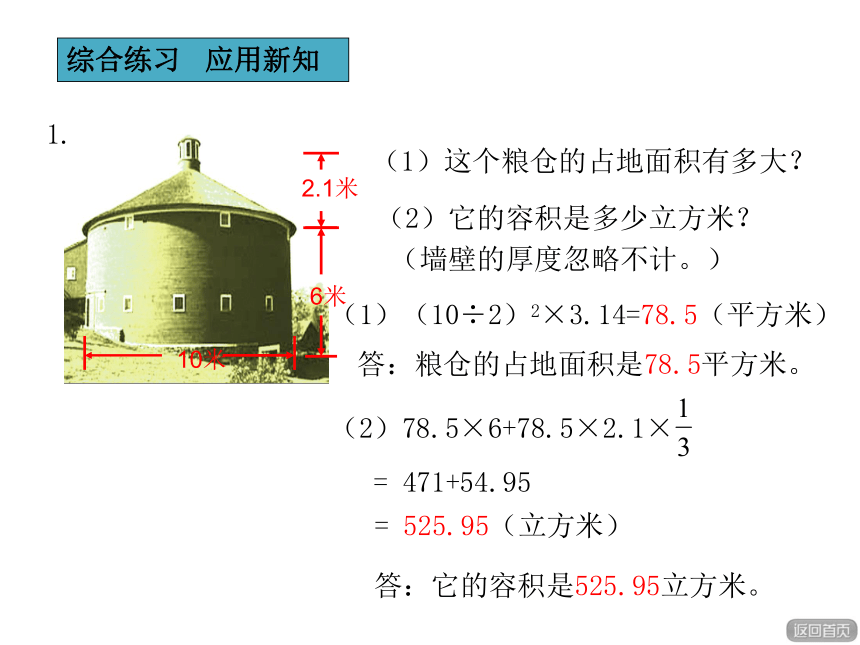
1.
(1)这个粮仓的占地面积有多大?
(2)它的容积是多少立方米?
(墙壁的厚度忽略不计。)
(1)(10÷2)2×3.14=78.5(平方米)
答:粮仓的占地面积是78.5平方米。
= 471+54.95
= 525.95(立方米)
答:它的容积是525.95立方米。
(2)78.5×6+78.5×2.1×
综合练习 应用新知
2.右图是从圆柱中挖去一个圆锥后的剩余部分,请计算
剩余部分的体积。(单位:cm)
圆柱体积是:
3.14 ×(12 ÷2)2 ×20=
2260.8 (cm3)
挖去圆锥的体积是:
376.8 (cm3)
3.14 ×(12 ÷2)2 ×10× =
2260.8-376.8=
1884( cm3)
答:剩余部分的体积是1884立方厘米。
3. 课本33页第1题。
①杯子的容积是多少立方厘米?
②每听饮料大约能倒几杯?
杯子的容积是:
3.14×(6÷2)2×4×
=
3.14×12
= 37.68(cm3)
杏仁露饮料的体积是:
3.14 ×(6 ÷ 2)2 ×12
=
3.14×9 ×12
= 339.12cm3
答:杯子的容积是37.68 (cm3)
答:每听饮料大约能倒9杯。
339.12 ÷37.68=
9 杯
4.右下图这个木桶的容底面直径是4分米,高5分米,这个木桶破损后最多能盛多少升水?
5cm=0.5dm
3.14×(4÷2)2×(5-0.5)
=
3.14×4×4.5
=56.52(立方分米)
=56.52(升)
答:这个木桶破损后最多能盛56.52升水。
拓展练习 发展新知
1.新课堂25页第4题:智慧园地。
要把右图中的圆柱削成与它
等高的圆锥零件,削去部分的体
积是多少立方厘米?
3.14 ×(6 ÷ 2)2 ×15 ×
=
3.14 ×9 ×10
=282.6立方厘米
答:削去部分的体积是282.6立方厘米。
2.如右下图所示,一个底面直径是20厘米的圆柱形玻璃杯中装有水,
水中放有一个底面直径为6厘米、高20厘米的圆锥形铅锤。当取出铅
锤后,杯里的水面会下降多少厘米?
圆柱的体积,圆锥的体积可以看作水面上升后新
的圆柱的体积,根据圆柱的底面直径20厘米,可
以利用s=π(d÷2)2求出圆柱的底面积,从而算出
圆柱的高也就是水面下降了多少厘米。
铅锤的体积是:
3.14×(6÷2)2×20× =
188.4(立方厘米)
圆柱的底面积:3.14×(20÷2)2=
314(平方厘米)
188.4÷314=
0.6(厘米)
答:杯里的水面下降0.6厘米。
3.瓶子里装着一些水(如下图所示),瓶底面积是0.8平方分米,请你想办法计算瓶子的容积。
0.8 × 2 = 1.6(立方分米)
0.8 ×(3-2.4)
0.48 + 1.6 = 2.08(立方分米)
答:瓶子的容积是2.08升。
= 0.8 ×0.6
= 0.48(立方分米)
2.08 立方分米 = 2.08 升
4. 沙漏又称沙钟,是我国古代的一种计量时间的仪器,它是根据
流沙从一个容器漏到另一个容器的数量来计量时间的。
你能求出这时沙漏上部和下部沙子的体积分别是多少吗?
沙漏上部沙子的体积:
3.14×(2÷2)2×3× =
3.14(立方厘米)
沙漏下部沙子的体积:
3.14×(6÷2)2×6× -3.14×1.52×(6-4.5)×
=56.52-3.5325
=52.9825(立方厘米)
答:沙漏上部沙子的体积是3.14立方厘米,下部沙子的体积是52.9825立方厘米。
三、梳理总结,提升认识。
教师总结:
通过这节课的练习,你对圆柱圆锥体积
的计算又有那些新的认识?
圆柱、圆锥体积练习
梳理总结 提升认识
分层练习 巩固提高
问题回顾 再现新知
一 、问题回顾 再现新知
圆柱体积=底面积×高
V圆柱=Sh
圆锥体积= 底面积×高×
V圆锥= Sh
圆柱体积推导演示
圆锥体积推导演示
小结:
基本练习,巩固新知
1.求下列图形的体积。(单位:厘米)
3.14 ×32 ×6.5=
3.14×(8÷2)2×6× =
183.69(cm3)
100.48( cm3 )
二、分层练习,巩固提高。
①圆柱体积是圆锥体积的3倍。( )
②一个圆锥体,底面积不变,高扩大6倍,体积也扩大6倍。( )
③把一个圆柱削成一个最大的圆锥,削去部分的体积是原体积的2/3。( )
④一个圆锥的体积是75立方米,底面积是25平方米,则它的高是3米。( )
2.判断题.
3. 如下图,直角三角形和长方形绕轴旋转一圈后,得到的立体图形是
什么形状的?它们的体积分别是多少立方厘米?
旋转后得到圆锥:r=5cm
h=7cm
3.14×52×7× ≈
183.17 (cm3)
旋转后得到圆柱:r=5.5cm
h=3cm
3.14×5.52×3 =
284.955 (cm3)
答:圆锥的体积大约是183.17 cm3
答:它的容积是284.955cm3 。
2.1米
10米
6米
1.
(1)这个粮仓的占地面积有多大?
(2)它的容积是多少立方米?
(墙壁的厚度忽略不计。)
(1)(10÷2)2×3.14=78.5(平方米)
答:粮仓的占地面积是78.5平方米。
= 471+54.95
= 525.95(立方米)
答:它的容积是525.95立方米。
(2)78.5×6+78.5×2.1×
综合练习 应用新知
2.右图是从圆柱中挖去一个圆锥后的剩余部分,请计算
剩余部分的体积。(单位:cm)
圆柱体积是:
3.14 ×(12 ÷2)2 ×20=
2260.8 (cm3)
挖去圆锥的体积是:
376.8 (cm3)
3.14 ×(12 ÷2)2 ×10× =
2260.8-376.8=
1884( cm3)
答:剩余部分的体积是1884立方厘米。
3. 课本33页第1题。
①杯子的容积是多少立方厘米?
②每听饮料大约能倒几杯?
杯子的容积是:
3.14×(6÷2)2×4×
=
3.14×12
= 37.68(cm3)
杏仁露饮料的体积是:
3.14 ×(6 ÷ 2)2 ×12
=
3.14×9 ×12
= 339.12cm3
答:杯子的容积是37.68 (cm3)
答:每听饮料大约能倒9杯。
339.12 ÷37.68=
9 杯
4.右下图这个木桶的容底面直径是4分米,高5分米,这个木桶破损后最多能盛多少升水?
5cm=0.5dm
3.14×(4÷2)2×(5-0.5)
=
3.14×4×4.5
=56.52(立方分米)
=56.52(升)
答:这个木桶破损后最多能盛56.52升水。
拓展练习 发展新知
1.新课堂25页第4题:智慧园地。
要把右图中的圆柱削成与它
等高的圆锥零件,削去部分的体
积是多少立方厘米?
3.14 ×(6 ÷ 2)2 ×15 ×
=
3.14 ×9 ×10
=282.6立方厘米
答:削去部分的体积是282.6立方厘米。
2.如右下图所示,一个底面直径是20厘米的圆柱形玻璃杯中装有水,
水中放有一个底面直径为6厘米、高20厘米的圆锥形铅锤。当取出铅
锤后,杯里的水面会下降多少厘米?
圆柱的体积,圆锥的体积可以看作水面上升后新
的圆柱的体积,根据圆柱的底面直径20厘米,可
以利用s=π(d÷2)2求出圆柱的底面积,从而算出
圆柱的高也就是水面下降了多少厘米。
铅锤的体积是:
3.14×(6÷2)2×20× =
188.4(立方厘米)
圆柱的底面积:3.14×(20÷2)2=
314(平方厘米)
188.4÷314=
0.6(厘米)
答:杯里的水面下降0.6厘米。
3.瓶子里装着一些水(如下图所示),瓶底面积是0.8平方分米,请你想办法计算瓶子的容积。
0.8 × 2 = 1.6(立方分米)
0.8 ×(3-2.4)
0.48 + 1.6 = 2.08(立方分米)
答:瓶子的容积是2.08升。
= 0.8 ×0.6
= 0.48(立方分米)
2.08 立方分米 = 2.08 升
4. 沙漏又称沙钟,是我国古代的一种计量时间的仪器,它是根据
流沙从一个容器漏到另一个容器的数量来计量时间的。
你能求出这时沙漏上部和下部沙子的体积分别是多少吗?
沙漏上部沙子的体积:
3.14×(2÷2)2×3× =
3.14(立方厘米)
沙漏下部沙子的体积:
3.14×(6÷2)2×6× -3.14×1.52×(6-4.5)×
=56.52-3.5325
=52.9825(立方厘米)
答:沙漏上部沙子的体积是3.14立方厘米,下部沙子的体积是52.9825立方厘米。
三、梳理总结,提升认识。
教师总结:
通过这节课的练习,你对圆柱圆锥体积
的计算又有那些新的认识?
