湖北省武汉市部分学校新2013届高三起点调研测试(数学文)
文档属性
| 名称 | 湖北省武汉市部分学校新2013届高三起点调研测试(数学文) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-09 00:00:00 | ||
图片预览



文档简介
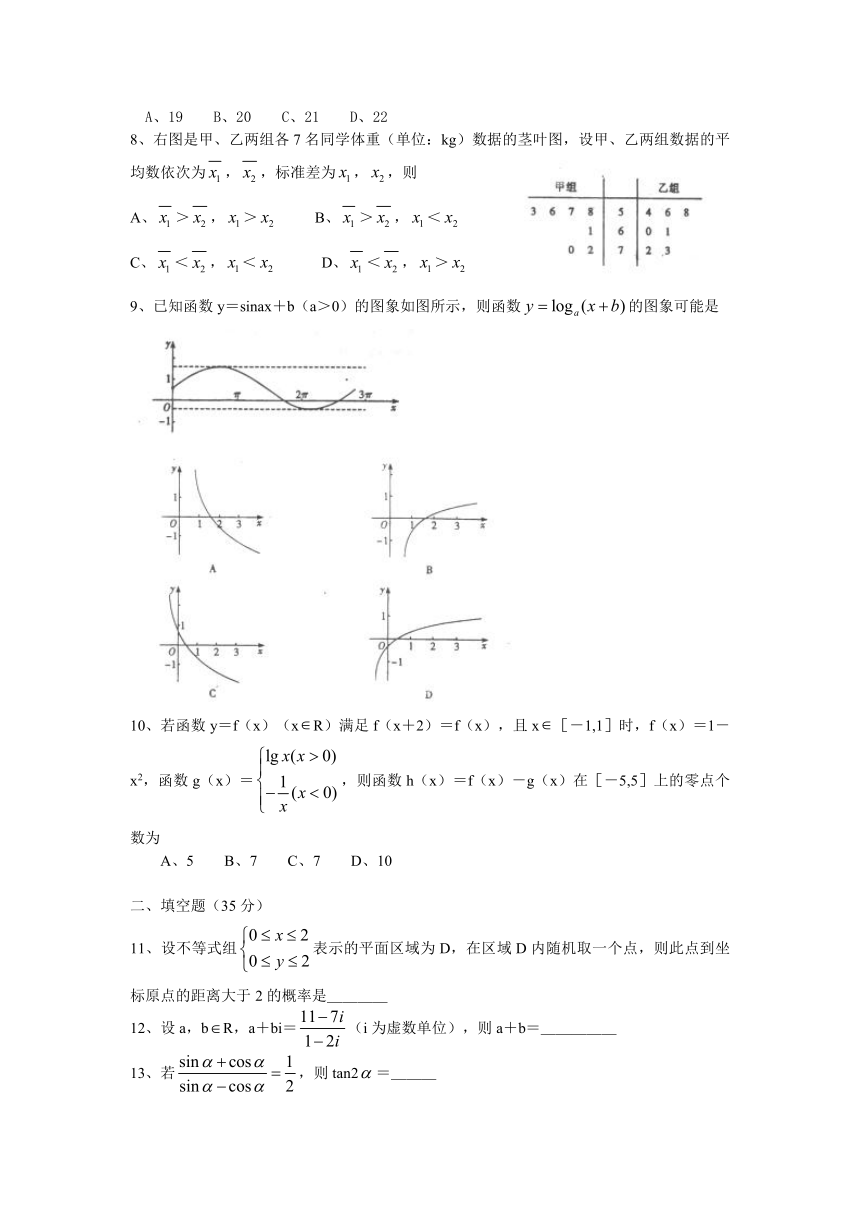
2012 --2013学年度
武汉市部分学校新高三起点调研测试
数学(文科)试卷 2012.9.7
一、选择题(50分)
1、设集合U={1,2,3,4,5,6},集合A={1,2,5},={4,5,6},则A∩B=
A、{1,2} B、{5} C、{1,2,3} D、{3,4,6}
2、下列命题中,真例题的是
A、,<0
B、,
C、“a+b=0”的充要条件是“=-1”
D、“a>1,b>1”是“ab>1“的充分条件
3、设xR,向量a=(x,1),b=(1,-2),且a⊥b,则|a+b|=
A、 B、 C、2 D、10
4、如图,中心均为原点O的双曲线与椭圆有公共焦点,M,N是双曲线的两顶点,若M,O,N将椭圆长轴四等分,则双曲线与椭圆的离心率的比值是
A、3 B、2
C、 D、
5、某程序框图如下图所示,该程序运行后输出的S的值是
A、-3 B、- C、 D、2
6、如上图是某几何体的三视图,则该几何体的体积为
A、16 B、24 C、34 D、48
7、已知公差不为0的等差数列{}的前n项和为Sn,S3=a4+6,且成等比数列,则a10=
A、19 B、20 C、21 D、22
8、右图是甲、乙两组各7名同学体重(单位:kg)数据的茎叶图,设甲、乙两组数据的平均数依次为,,标准差为,,则
A、>,> B、>,<
C、<,< D、<,>
9、已知函数y=sinax+b(a>0)的图象如图所示,则函数的图象可能是
10、若函数y=f(x)(xR)满足f(x+2)=f(x),且x[-1,1]时,f(x)=1-x2,函数g(x)=,则函数h(x)=f(x)-g(x)在[-5,5]上的零点个数为
A、5 B、7 C、7 D、10
二、填空题(35分)
11、设不等式组表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是____
12、设a,bR,a+bi=(i为虚数单位),则a+b=_____
13、若,则tan2=___
14、某地区恩格尔系数y(%)与年份x统计数据如下表:
从散点图可以看出y与x线性相关,且可得回归方程为,则=___,据此模型可预测2012年该地区的恩格尔系数(%)为____
15、已知圆柱M的底面半径与球O的半径相同,且圆柱M与球O的表面积相等,则它们的体积之比=____
16、已知等差数列{}的首项及公差均为正数,令(,n<2012),当是数列{}的最大项时,k=____
17、已知△FAB,点F的坐标为(1,0),点A,B分别在图中抛物线y2=4x及圆(x-1)2+y2=4的实线部分上运动,且AB总是平行于x轴,,则△FAB的周长的取值范围是____
三、解答题(75分)
18、(本小题满分12分)
某研究性学习小组对昼夜温差与某种子发芽数的关系进行研究,他们分别记录了四天中每天昼夜温差与每天100粒种子浸泡后的发芽数,得到如下资料:
(I)求这四天浸泡种子的平均发芽率;
(II)若研究的一个项目在这四天中任选2天的种子发芽数来进行,记发芽的种子数分别为m,n(m<n),则(m,n)的形式列出所有的基本事件,并求“m,n满足”的事件A的概率。
19、(本小题满分12分)
已知函数的图象过点M(,0)。
(I)求m的值;
(II)在△ABC中,角A,B,C的对边分别是a,b,c,若ccosB+bcosC=2acosB,求f(A)的取值范围。
20、(本小题满分12分)
在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2, M是棱CC1的中点。
(I)求异面直线A1M和C1D1所成角的正切值;
(II)求证:平面 ABM⊥平面A1B1M
21、(本小题满分14分)
已知函数。其中a>0。
(I)当a=1时,求曲线y=f(x)在(2,f(2))处的切线方程;
(II)若在区间[-,]上,f(x)>0恒成立,求a的取值范围。
22、(本小题满分14分)
已知椭圆C:的右焦点为F(1,0),且点(-1,)在椭圆C上。
(I)求椭圆C的标准方程;
(II)已知动直线l过点F,且与椭圆C交于A,B两点,试问x轴上是否存在定点Q,使得恒成立?若存在 ,求出点Q的坐标,若不存在,请说明理由。
武汉市部分学校新高三起点调研测试
数学(文科)试卷 2012.9.7
一、选择题(50分)
1、设集合U={1,2,3,4,5,6},集合A={1,2,5},={4,5,6},则A∩B=
A、{1,2} B、{5} C、{1,2,3} D、{3,4,6}
2、下列命题中,真例题的是
A、,<0
B、,
C、“a+b=0”的充要条件是“=-1”
D、“a>1,b>1”是“ab>1“的充分条件
3、设xR,向量a=(x,1),b=(1,-2),且a⊥b,则|a+b|=
A、 B、 C、2 D、10
4、如图,中心均为原点O的双曲线与椭圆有公共焦点,M,N是双曲线的两顶点,若M,O,N将椭圆长轴四等分,则双曲线与椭圆的离心率的比值是
A、3 B、2
C、 D、
5、某程序框图如下图所示,该程序运行后输出的S的值是
A、-3 B、- C、 D、2
6、如上图是某几何体的三视图,则该几何体的体积为
A、16 B、24 C、34 D、48
7、已知公差不为0的等差数列{}的前n项和为Sn,S3=a4+6,且成等比数列,则a10=
A、19 B、20 C、21 D、22
8、右图是甲、乙两组各7名同学体重(单位:kg)数据的茎叶图,设甲、乙两组数据的平均数依次为,,标准差为,,则
A、>,> B、>,<
C、<,< D、<,>
9、已知函数y=sinax+b(a>0)的图象如图所示,则函数的图象可能是
10、若函数y=f(x)(xR)满足f(x+2)=f(x),且x[-1,1]时,f(x)=1-x2,函数g(x)=,则函数h(x)=f(x)-g(x)在[-5,5]上的零点个数为
A、5 B、7 C、7 D、10
二、填空题(35分)
11、设不等式组表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是____
12、设a,bR,a+bi=(i为虚数单位),则a+b=_____
13、若,则tan2=___
14、某地区恩格尔系数y(%)与年份x统计数据如下表:
从散点图可以看出y与x线性相关,且可得回归方程为,则=___,据此模型可预测2012年该地区的恩格尔系数(%)为____
15、已知圆柱M的底面半径与球O的半径相同,且圆柱M与球O的表面积相等,则它们的体积之比=____
16、已知等差数列{}的首项及公差均为正数,令(,n<2012),当是数列{}的最大项时,k=____
17、已知△FAB,点F的坐标为(1,0),点A,B分别在图中抛物线y2=4x及圆(x-1)2+y2=4的实线部分上运动,且AB总是平行于x轴,,则△FAB的周长的取值范围是____
三、解答题(75分)
18、(本小题满分12分)
某研究性学习小组对昼夜温差与某种子发芽数的关系进行研究,他们分别记录了四天中每天昼夜温差与每天100粒种子浸泡后的发芽数,得到如下资料:
(I)求这四天浸泡种子的平均发芽率;
(II)若研究的一个项目在这四天中任选2天的种子发芽数来进行,记发芽的种子数分别为m,n(m<n),则(m,n)的形式列出所有的基本事件,并求“m,n满足”的事件A的概率。
19、(本小题满分12分)
已知函数的图象过点M(,0)。
(I)求m的值;
(II)在△ABC中,角A,B,C的对边分别是a,b,c,若ccosB+bcosC=2acosB,求f(A)的取值范围。
20、(本小题满分12分)
在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2, M是棱CC1的中点。
(I)求异面直线A1M和C1D1所成角的正切值;
(II)求证:平面 ABM⊥平面A1B1M
21、(本小题满分14分)
已知函数。其中a>0。
(I)当a=1时,求曲线y=f(x)在(2,f(2))处的切线方程;
(II)若在区间[-,]上,f(x)>0恒成立,求a的取值范围。
22、(本小题满分14分)
已知椭圆C:的右焦点为F(1,0),且点(-1,)在椭圆C上。
(I)求椭圆C的标准方程;
(II)已知动直线l过点F,且与椭圆C交于A,B两点,试问x轴上是否存在定点Q,使得恒成立?若存在 ,求出点Q的坐标,若不存在,请说明理由。
同课章节目录
