第12章整式的乘除 同步练习题 2021-2022学年华师大版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 第12章整式的乘除 同步练习题 2021-2022学年华师大版八年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 149.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 09:57:35 | ||
图片预览



文档简介
2021-2022学年华师大版八年级数学上册《第12章整式的乘除》同步练习题(附答案)
一.选择题
1.已知xm=a,xn=b(x≠0),则x3m﹣2n的值等于( )
A.3a﹣2b B.a3﹣b2 C.a3b2 D.
2.下列运算正确的是( )
A.(x2)3+(x3)2=2x6 B.(x2)3 (x2)3=2x12
C.x4 (2x)2=2x6 D.(2x)3 (﹣x)2=﹣8x5
3.如果x2﹣(m+1)x+1是完全平方式,则m的值为( )
A.﹣1 B.1 C.1或﹣1 D.1或﹣3
4.7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A.a=b B.a=3b C.a=b D.a=4b
5.多项式mx2﹣m与多项式x2﹣2x+1的公因式是( )
A.x﹣1 B.x+1 C.x2﹣1 D.(x﹣1)2
6.把多项式4x2y﹣4xy2﹣x3分解因式的结果是( )
A.4xy(x﹣y)﹣x3 B.﹣x(x﹣2y)2
C.x(4xy﹣4y2﹣x2) D.﹣x(﹣4xy+4y2+x2)
7.下面的多项式在实数范围内能因式分解的是( )
A.x2+y2 B.x2﹣y C.x2+x+1 D.x2﹣2x+1
二.填空题
8.已知关于x的三次三项式2x3+3x﹣k有一个因式是2x﹣5,则另一个因式为 .
9.分解因式:y3﹣3y2﹣4y= .
10.因式分解:a2b﹣4ab+4b= .
11.计算:(﹣3)2023 (﹣)2021= .
12.若m为正实数,且m﹣=3,则m2﹣= .
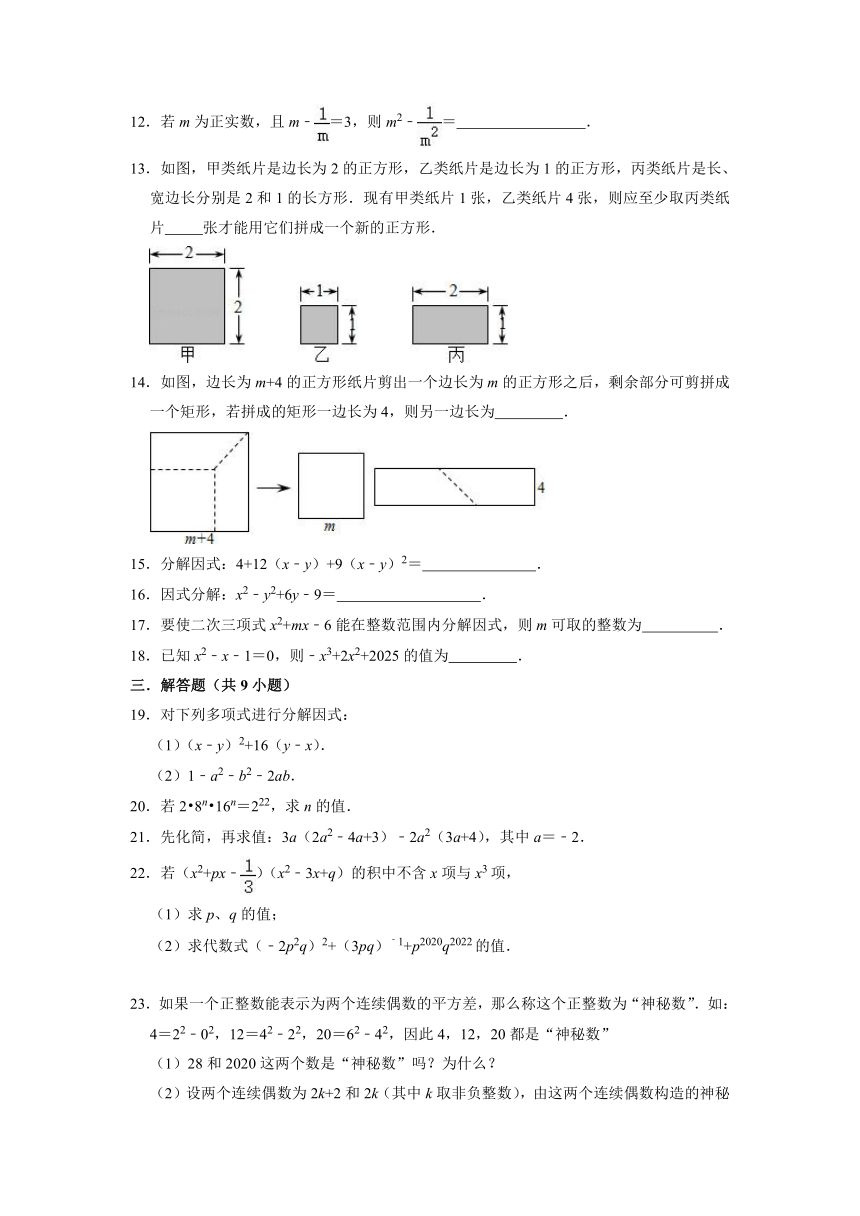
13.如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长、宽边长分别是2和1的长方形.现有甲类纸片1张,乙类纸片4张,则应至少取丙类纸片 张才能用它们拼成一个新的正方形.
14.如图,边长为m+4的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为 .
15.分解因式:4+12(x﹣y)+9(x﹣y)2= .
16.因式分解:x2﹣y2+6y﹣9= .
17.要使二次三项式x2+mx﹣6能在整数范围内分解因式,则m可取的整数为 .
18.已知x2﹣x﹣1=0,则﹣x3+2x2+2025的值为 .
三.解答题(共9小题)
19.对下列多项式进行分解因式:
(1)(x﹣y)2+16(y﹣x).
(2)1﹣a2﹣b2﹣2ab.
20.若2 8n 16n=222,求n的值.
21.先化简,再求值:3a(2a2﹣4a+3)﹣2a2(3a+4),其中a=﹣2.
22.若(x2+px﹣)(x2﹣3x+q)的积中不含x项与x3项,
(1)求p、q的值;
(2)求代数式(﹣2p2q)2+(3pq)﹣1+p2020q2022的值.
23.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22﹣02,12=42﹣22,20=62﹣42,因此4,12,20都是“神秘数”
(1)28和2020这两个数是“神秘数”吗?为什么?
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
(3)两个连续奇数的平方差(k取正数)是神秘数吗?为什么?
24.观察下列各式:
(x﹣1)÷(x﹣1)=1;
(x2﹣1)÷(x﹣1)=x+1;
(x3﹣1)÷(x﹣1)=x2+x+1;
(x4﹣1)÷(x﹣1)=x3+x2+x+1;
(1)根据上面各式的规律可得(xn+1﹣1)÷(x﹣1)= ;
(2)利用(1)的结论求22021+22020+…+2+1的值;
(3)若1+x+x2+…+x2021=0,求x2022的值.
25.先化简,再求值:(2+a)(2﹣a)+a(a﹣5b)+3a5b3÷(﹣a2b)2,其中ab=﹣.
26.仔细阅读下面例题,解答问题:
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得
x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴.
解得:n=﹣7,m=﹣21
∴另一个因式为(x﹣7),m的值为﹣21
问题:仿照以上方法解答下面问题:
已知二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
27.因式分解:
(1)2x(a﹣b)+3y(b﹣a)
(2)x(x2﹣xy)﹣(4x2﹣4xy)
参考答案
1.解:∵xm=a,xn=b(x≠0),
∴x3m﹣2n=x3m÷x2n=.
故选:D.
2.解:A、原式=x6+x6=2x6,故A正确;
B、原式=x6 x6=x12,故B错误;
C、原式=x4 4x2=4x6,故C错误;
D、原式=8x3 x2=8x5,故D错误;
故选:A.
3.解:∵x2﹣(m+1)x+1是完全平方式,
∴﹣(m+1)x=±2×1 x,
解得:m=1或m=﹣3.
故选:D.
4.解:左上角阴影部分的长为AE,宽为AF=3b,右下角阴影部分的长为PC,宽为a,
∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC,
∴AE+a=4b+PC,即AE﹣PC=4b﹣a,
∴阴影部分面积之差S=AE AF﹣PC CG=3bAE﹣aPC=3b(PC+4b﹣a)﹣aPC=(3b﹣a)PC+12b2﹣3ab,
则3b﹣a=0,即a=3b.
解法二:既然BC是变化的,当点P与点C重合开始,然后BC向右伸展,
设向右伸展长度为X,左上阴影增加的是3bX,右下阴影增加的是aX,因为S不变,
∴增加的面积相等,
∴3bX=aX,
∴a=3b.
故选:B.
5.解:mx2﹣m=m(x﹣1)(x+1),
x2﹣2x+1=(x﹣1)2,
多项式mx2﹣m与多项式x2﹣2x+1的公因式是(x﹣1).
故选:A.
6.解:4x2y﹣4xy2﹣x3
=﹣x(x2﹣4xy+4y2)
=﹣x(x﹣2y)2,
故选:B.
7.解;A、x2+y2,无法因式分解,故A选项错误;
B、x2﹣y,无法因式分解,故B选项错误;
C、x2+x+1,无法因式分解,故C选项错误;
D、x2﹣2x+1=(x﹣1)2,故D选项正确.
故选:D.
8.解:设另一个因式为x2+ax+b,
则2x3+3x﹣k=(2x﹣5)(x2+ax+b)=2x3+(2a﹣5)x2+(2b﹣5a)x﹣5b,
所以,
解得:a=2.5,b=,
即另一个因式为x2+2.5x+,
故答案为:x2+2.5x+.
9.解:原式=y(y2﹣3y﹣4)=y(y+1)(y﹣4),
故答案为:y(y+1)(y﹣4)
10.解:原式=b(a2﹣4a+4)=b(a﹣2)2,
故答案为:b(a﹣2)2
11.解:(﹣3)2023×(﹣)2021
=(﹣3)2×(﹣3)2021×(﹣)2021
=(﹣3)2×[﹣3×(﹣)]2021
=(﹣3)2
=9,
故答案为:9.
12.解:法一:由得,
得m2﹣3m﹣1=0,即=,
∴m1=,m2=,
因为m为正实数,∴m=,
∴=()()
=3×(),
=3×,
=;
法二:由平方得:m2+﹣2=9,
m2++2=13,即(m+)2=13,又m为正实数,
∴m+=,
则=(m+)(m﹣)=3.
故答案为:.
13.解:甲类纸片1张,乙类纸片4张,总面积是4+4=8,大于8的完全平方数依次是9,16,25…,而丙的面积是2,因而不可能是9;
当总面积是16时,取的丙纸片的总面积是8,因而是4张.
因而应至少取丙类纸片4张才能用它们拼成一个新的正方形.
故答案为:4.
14.解:设拼成的矩形的另一边长为x,
则4x=(m+4)2﹣m2=(m+4+m)(m+4﹣m),
解得x=2m+4.
故答案为:2m+4.
15.解:原式=[2+3(x﹣y)]2=(3x﹣3y+2)2.
故答案为:(3x﹣3y+2)2
16.解:x2﹣y2+6y﹣9,
=x2﹣(y2﹣6y+9),
=x2﹣(y﹣3)2,
=(x﹣y+3)(x+y﹣3).
17.解:∵﹣6=2×(﹣3)=(﹣2)×3=1×(﹣6)=(﹣1)×6,
∴m=2+(﹣3)=﹣1,m=﹣2+3=1,m=1+(﹣6)=﹣5,m=(﹣1)+6=5,
故本题答案为:±1,±5.
18.解:∵x2﹣x﹣1=0,
∴x2﹣x=1,
∴﹣x3+2x2+2025,
=﹣x(x2﹣x)+x2+2025,
=﹣x+x2+2025,
=2026.
故答案为:2026.
三.解答题(共9小题)
19.解:(1)原式=(x﹣y)2﹣16(x﹣y)=(x﹣y)(x﹣y﹣16);
(2)原式=1﹣(a2+b2+2ab)=1﹣(a+b)2=(1+a+b)(1﹣a﹣b).
20.解:2 8n 16n,
=2×23n×24n,
=27n+1,
∵2 8n 16n=222,
∴7n+1=22,
解得n=3.
21.解:3a(2a2﹣4a+3)﹣2a2(3a+4)
=6a3﹣12a2+9a﹣6a3﹣8a2
=﹣20a2+9a,
当a=﹣2时,原式=﹣20×4﹣9×2=﹣98.
22.解:(1)(x2+px﹣)(x2﹣3x+q)=x4+(p﹣3)x3+(q﹣3p﹣)x2+(qp+1)x﹣q,
∵积中不含x项与x3项,
∴p﹣3=0,qp+1=0
∴p=3,q=﹣,
(2)(﹣2p2q)2+(3pq)﹣1+p2020q2022
=36﹣+
=35.
23.解:(1)设28和2012都是“神秘数”,设28是x和x﹣2两数的平方差得到,
则x2﹣(x﹣2)2=28,
解得:x=8,∴x﹣2=6,
即28=82﹣62,
设2020是y和y﹣2两数的平方差得到,
则y2﹣(y﹣2)2=2020,
解得:y=506,
y﹣2=504,
即2020=5062﹣5042,
所以28,2020都是神秘数.
(2)(2k+2)2﹣(2k)2=(2k+2﹣2k)(2k+2+2k)=4(2k+1),
∴由2k+2和2k构造的神秘数是4的倍数,且是奇数倍.
(3)设两个连续奇数为2k+1和2k﹣1,
则(2k+1)2﹣(2k﹣1)2=8k=4×2k,
即:两个连续奇数的平方差是4的倍数,是偶数倍,不满足连续偶数的神秘数为4的奇数倍这一条件.
∴两个连续奇数的平方差不是神秘数.
24.解:(1)由已知发现,结果的规律:按x进行降幂排列,各项系数为1,最高次项的次数为等式前面的最高次数减1,
可知:(xn+1﹣1)÷(x﹣1)=xn+xn﹣1+…+x+1,
(2)22021+22020+…+2+1=(22022﹣1)÷(2﹣1)=22022﹣1;
(3)由1+x+x2+…+x2021=0可得,
(x2022﹣1)÷(x﹣1)=0,
∴x2022﹣1=0且x﹣1≠0,
∴x2022=1.
25.解:原式=4﹣a2+a2﹣5ab+3ab=4﹣2ab,
当ab=﹣时,原式=4+1=5.
26.解:设另一个因式为(x+a),得(1分)
2x2+3x﹣k=(2x﹣5)(x+a)(2分)
则2x2+3x﹣k=2x2+(2a﹣5)x﹣5a(4分)
∴(6分)
解得:a=4,k=20(8分)
故另一个因式为(x+4),k的值为20(9分)
27.解:(1)原式=2x(a﹣b)﹣3y(a﹣b)=(a﹣b)(2x﹣3y);
(2)原式=x2(x﹣y)﹣4x(x﹣y)=x(x﹣y)(x﹣4)
一.选择题
1.已知xm=a,xn=b(x≠0),则x3m﹣2n的值等于( )
A.3a﹣2b B.a3﹣b2 C.a3b2 D.
2.下列运算正确的是( )
A.(x2)3+(x3)2=2x6 B.(x2)3 (x2)3=2x12
C.x4 (2x)2=2x6 D.(2x)3 (﹣x)2=﹣8x5
3.如果x2﹣(m+1)x+1是完全平方式,则m的值为( )
A.﹣1 B.1 C.1或﹣1 D.1或﹣3
4.7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A.a=b B.a=3b C.a=b D.a=4b
5.多项式mx2﹣m与多项式x2﹣2x+1的公因式是( )
A.x﹣1 B.x+1 C.x2﹣1 D.(x﹣1)2
6.把多项式4x2y﹣4xy2﹣x3分解因式的结果是( )
A.4xy(x﹣y)﹣x3 B.﹣x(x﹣2y)2
C.x(4xy﹣4y2﹣x2) D.﹣x(﹣4xy+4y2+x2)
7.下面的多项式在实数范围内能因式分解的是( )
A.x2+y2 B.x2﹣y C.x2+x+1 D.x2﹣2x+1
二.填空题
8.已知关于x的三次三项式2x3+3x﹣k有一个因式是2x﹣5,则另一个因式为 .
9.分解因式:y3﹣3y2﹣4y= .
10.因式分解:a2b﹣4ab+4b= .
11.计算:(﹣3)2023 (﹣)2021= .
12.若m为正实数,且m﹣=3,则m2﹣= .
13.如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长、宽边长分别是2和1的长方形.现有甲类纸片1张,乙类纸片4张,则应至少取丙类纸片 张才能用它们拼成一个新的正方形.
14.如图,边长为m+4的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为 .
15.分解因式:4+12(x﹣y)+9(x﹣y)2= .
16.因式分解:x2﹣y2+6y﹣9= .
17.要使二次三项式x2+mx﹣6能在整数范围内分解因式,则m可取的整数为 .
18.已知x2﹣x﹣1=0,则﹣x3+2x2+2025的值为 .
三.解答题(共9小题)
19.对下列多项式进行分解因式:
(1)(x﹣y)2+16(y﹣x).
(2)1﹣a2﹣b2﹣2ab.
20.若2 8n 16n=222,求n的值.
21.先化简,再求值:3a(2a2﹣4a+3)﹣2a2(3a+4),其中a=﹣2.
22.若(x2+px﹣)(x2﹣3x+q)的积中不含x项与x3项,
(1)求p、q的值;
(2)求代数式(﹣2p2q)2+(3pq)﹣1+p2020q2022的值.
23.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22﹣02,12=42﹣22,20=62﹣42,因此4,12,20都是“神秘数”
(1)28和2020这两个数是“神秘数”吗?为什么?
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
(3)两个连续奇数的平方差(k取正数)是神秘数吗?为什么?
24.观察下列各式:
(x﹣1)÷(x﹣1)=1;
(x2﹣1)÷(x﹣1)=x+1;
(x3﹣1)÷(x﹣1)=x2+x+1;
(x4﹣1)÷(x﹣1)=x3+x2+x+1;
(1)根据上面各式的规律可得(xn+1﹣1)÷(x﹣1)= ;
(2)利用(1)的结论求22021+22020+…+2+1的值;
(3)若1+x+x2+…+x2021=0,求x2022的值.
25.先化简,再求值:(2+a)(2﹣a)+a(a﹣5b)+3a5b3÷(﹣a2b)2,其中ab=﹣.
26.仔细阅读下面例题,解答问题:
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得
x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴.
解得:n=﹣7,m=﹣21
∴另一个因式为(x﹣7),m的值为﹣21
问题:仿照以上方法解答下面问题:
已知二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
27.因式分解:
(1)2x(a﹣b)+3y(b﹣a)
(2)x(x2﹣xy)﹣(4x2﹣4xy)
参考答案
1.解:∵xm=a,xn=b(x≠0),
∴x3m﹣2n=x3m÷x2n=.
故选:D.
2.解:A、原式=x6+x6=2x6,故A正确;
B、原式=x6 x6=x12,故B错误;
C、原式=x4 4x2=4x6,故C错误;
D、原式=8x3 x2=8x5,故D错误;
故选:A.
3.解:∵x2﹣(m+1)x+1是完全平方式,
∴﹣(m+1)x=±2×1 x,
解得:m=1或m=﹣3.
故选:D.
4.解:左上角阴影部分的长为AE,宽为AF=3b,右下角阴影部分的长为PC,宽为a,
∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC,
∴AE+a=4b+PC,即AE﹣PC=4b﹣a,
∴阴影部分面积之差S=AE AF﹣PC CG=3bAE﹣aPC=3b(PC+4b﹣a)﹣aPC=(3b﹣a)PC+12b2﹣3ab,
则3b﹣a=0,即a=3b.
解法二:既然BC是变化的,当点P与点C重合开始,然后BC向右伸展,
设向右伸展长度为X,左上阴影增加的是3bX,右下阴影增加的是aX,因为S不变,
∴增加的面积相等,
∴3bX=aX,
∴a=3b.
故选:B.
5.解:mx2﹣m=m(x﹣1)(x+1),
x2﹣2x+1=(x﹣1)2,
多项式mx2﹣m与多项式x2﹣2x+1的公因式是(x﹣1).
故选:A.
6.解:4x2y﹣4xy2﹣x3
=﹣x(x2﹣4xy+4y2)
=﹣x(x﹣2y)2,
故选:B.
7.解;A、x2+y2,无法因式分解,故A选项错误;
B、x2﹣y,无法因式分解,故B选项错误;
C、x2+x+1,无法因式分解,故C选项错误;
D、x2﹣2x+1=(x﹣1)2,故D选项正确.
故选:D.
8.解:设另一个因式为x2+ax+b,
则2x3+3x﹣k=(2x﹣5)(x2+ax+b)=2x3+(2a﹣5)x2+(2b﹣5a)x﹣5b,
所以,
解得:a=2.5,b=,
即另一个因式为x2+2.5x+,
故答案为:x2+2.5x+.
9.解:原式=y(y2﹣3y﹣4)=y(y+1)(y﹣4),
故答案为:y(y+1)(y﹣4)
10.解:原式=b(a2﹣4a+4)=b(a﹣2)2,
故答案为:b(a﹣2)2
11.解:(﹣3)2023×(﹣)2021
=(﹣3)2×(﹣3)2021×(﹣)2021
=(﹣3)2×[﹣3×(﹣)]2021
=(﹣3)2
=9,
故答案为:9.
12.解:法一:由得,
得m2﹣3m﹣1=0,即=,
∴m1=,m2=,
因为m为正实数,∴m=,
∴=()()
=3×(),
=3×,
=;
法二:由平方得:m2+﹣2=9,
m2++2=13,即(m+)2=13,又m为正实数,
∴m+=,
则=(m+)(m﹣)=3.
故答案为:.
13.解:甲类纸片1张,乙类纸片4张,总面积是4+4=8,大于8的完全平方数依次是9,16,25…,而丙的面积是2,因而不可能是9;
当总面积是16时,取的丙纸片的总面积是8,因而是4张.
因而应至少取丙类纸片4张才能用它们拼成一个新的正方形.
故答案为:4.
14.解:设拼成的矩形的另一边长为x,
则4x=(m+4)2﹣m2=(m+4+m)(m+4﹣m),
解得x=2m+4.
故答案为:2m+4.
15.解:原式=[2+3(x﹣y)]2=(3x﹣3y+2)2.
故答案为:(3x﹣3y+2)2
16.解:x2﹣y2+6y﹣9,
=x2﹣(y2﹣6y+9),
=x2﹣(y﹣3)2,
=(x﹣y+3)(x+y﹣3).
17.解:∵﹣6=2×(﹣3)=(﹣2)×3=1×(﹣6)=(﹣1)×6,
∴m=2+(﹣3)=﹣1,m=﹣2+3=1,m=1+(﹣6)=﹣5,m=(﹣1)+6=5,
故本题答案为:±1,±5.
18.解:∵x2﹣x﹣1=0,
∴x2﹣x=1,
∴﹣x3+2x2+2025,
=﹣x(x2﹣x)+x2+2025,
=﹣x+x2+2025,
=2026.
故答案为:2026.
三.解答题(共9小题)
19.解:(1)原式=(x﹣y)2﹣16(x﹣y)=(x﹣y)(x﹣y﹣16);
(2)原式=1﹣(a2+b2+2ab)=1﹣(a+b)2=(1+a+b)(1﹣a﹣b).
20.解:2 8n 16n,
=2×23n×24n,
=27n+1,
∵2 8n 16n=222,
∴7n+1=22,
解得n=3.
21.解:3a(2a2﹣4a+3)﹣2a2(3a+4)
=6a3﹣12a2+9a﹣6a3﹣8a2
=﹣20a2+9a,
当a=﹣2时,原式=﹣20×4﹣9×2=﹣98.
22.解:(1)(x2+px﹣)(x2﹣3x+q)=x4+(p﹣3)x3+(q﹣3p﹣)x2+(qp+1)x﹣q,
∵积中不含x项与x3项,
∴p﹣3=0,qp+1=0
∴p=3,q=﹣,
(2)(﹣2p2q)2+(3pq)﹣1+p2020q2022
=36﹣+
=35.
23.解:(1)设28和2012都是“神秘数”,设28是x和x﹣2两数的平方差得到,
则x2﹣(x﹣2)2=28,
解得:x=8,∴x﹣2=6,
即28=82﹣62,
设2020是y和y﹣2两数的平方差得到,
则y2﹣(y﹣2)2=2020,
解得:y=506,
y﹣2=504,
即2020=5062﹣5042,
所以28,2020都是神秘数.
(2)(2k+2)2﹣(2k)2=(2k+2﹣2k)(2k+2+2k)=4(2k+1),
∴由2k+2和2k构造的神秘数是4的倍数,且是奇数倍.
(3)设两个连续奇数为2k+1和2k﹣1,
则(2k+1)2﹣(2k﹣1)2=8k=4×2k,
即:两个连续奇数的平方差是4的倍数,是偶数倍,不满足连续偶数的神秘数为4的奇数倍这一条件.
∴两个连续奇数的平方差不是神秘数.
24.解:(1)由已知发现,结果的规律:按x进行降幂排列,各项系数为1,最高次项的次数为等式前面的最高次数减1,
可知:(xn+1﹣1)÷(x﹣1)=xn+xn﹣1+…+x+1,
(2)22021+22020+…+2+1=(22022﹣1)÷(2﹣1)=22022﹣1;
(3)由1+x+x2+…+x2021=0可得,
(x2022﹣1)÷(x﹣1)=0,
∴x2022﹣1=0且x﹣1≠0,
∴x2022=1.
25.解:原式=4﹣a2+a2﹣5ab+3ab=4﹣2ab,
当ab=﹣时,原式=4+1=5.
26.解:设另一个因式为(x+a),得(1分)
2x2+3x﹣k=(2x﹣5)(x+a)(2分)
则2x2+3x﹣k=2x2+(2a﹣5)x﹣5a(4分)
∴(6分)
解得:a=4,k=20(8分)
故另一个因式为(x+4),k的值为20(9分)
27.解:(1)原式=2x(a﹣b)﹣3y(a﹣b)=(a﹣b)(2x﹣3y);
(2)原式=x2(x﹣y)﹣4x(x﹣y)=x(x﹣y)(x﹣4)
