第4章 图形的初步认识 常考题套卷 2020-2021学年华东师大版七年级数学上册(Word版 含答案)
文档属性
| 名称 | 第4章 图形的初步认识 常考题套卷 2020-2021学年华东师大版七年级数学上册(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 592.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 00:00:00 | ||
图片预览


文档简介
2020年华东师大新版七年级(上)《第4章 图形的初步认识》常考题套卷(3)
一、选择题
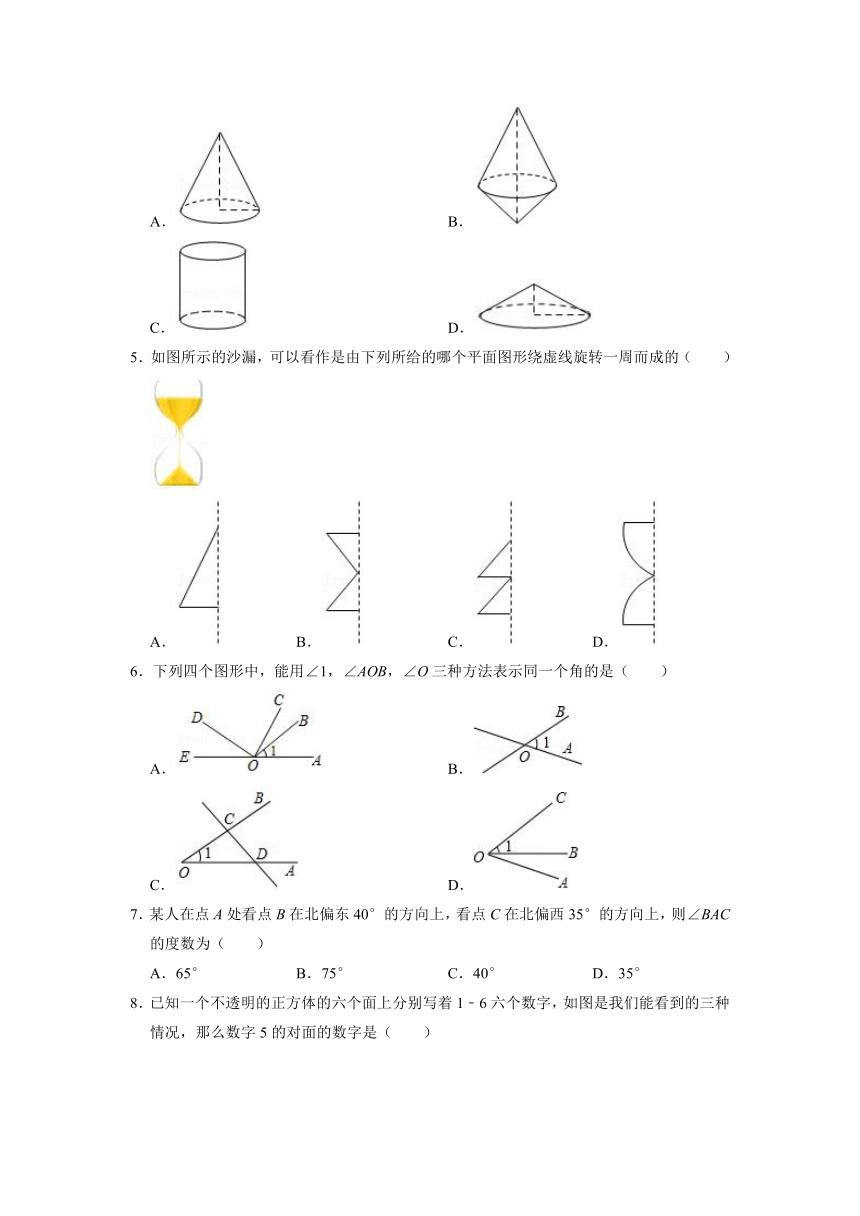
1.将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )
A.
B.
C.
D.
2.如图,观察图形,下列结论中不正确的是( )
A.直线BA和直线AB是同一条直线
B.图中有5条线段
C.AB+BD>AD
D.射线AC和射线AD是同一条射线
3.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm B.3cm C.7cm或3cm D.5cm
4.如下图,将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是( )
A. B.
C. D.
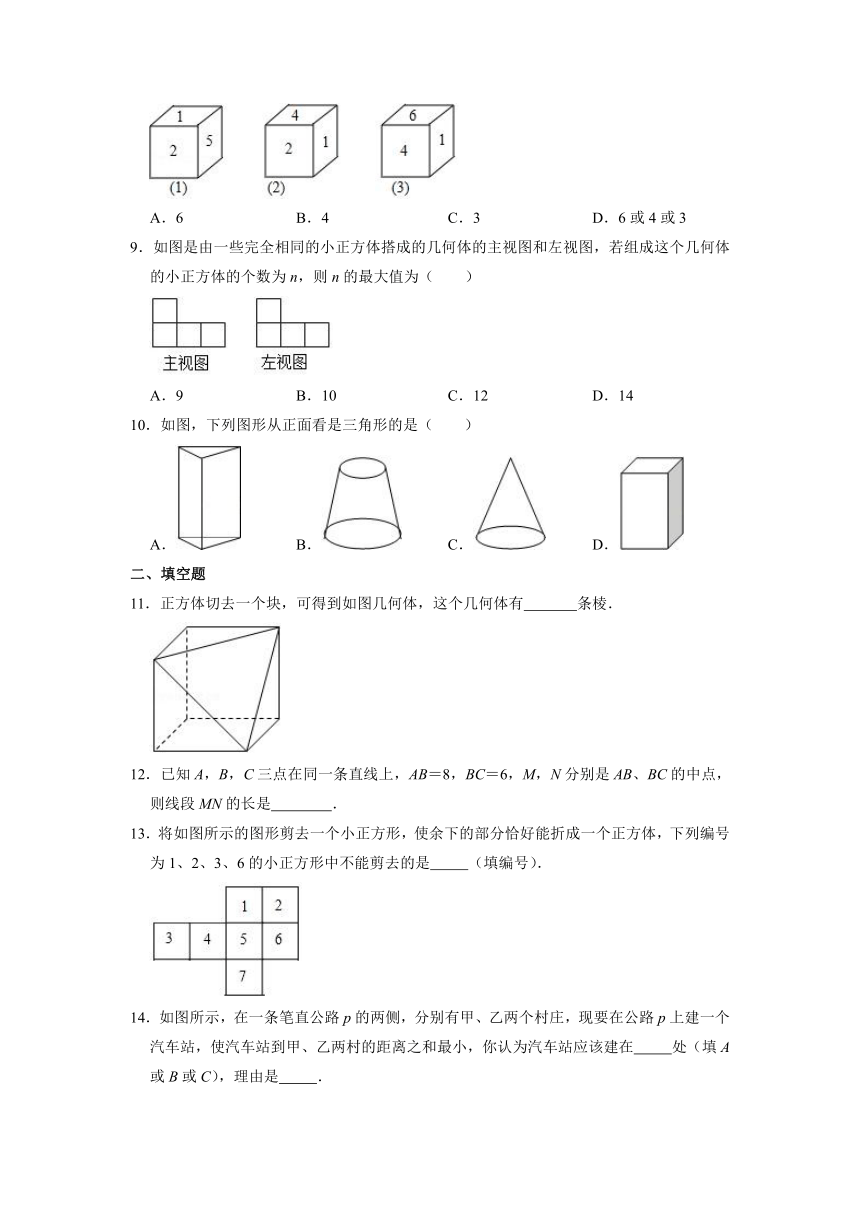
5.如图所示的沙漏,可以看作是由下列所给的哪个平面图形绕虚线旋转一周而成的( )
A. B. C. D.
6.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )
A. B.
C. D.
7.某人在点A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,则∠BAC的度数为( )
A.65° B.75° C.40° D.35°
8.已知一个不透明的正方体的六个面上分别写着1﹣6六个数字,如图是我们能看到的三种情况,那么数字5的对面的数字是( )
A.6 B.4 C.3 D.6或4或3
9.如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,若组成这个几何体的小正方体的个数为n,则n的最大值为( )
A.9 B.10 C.12 D.14
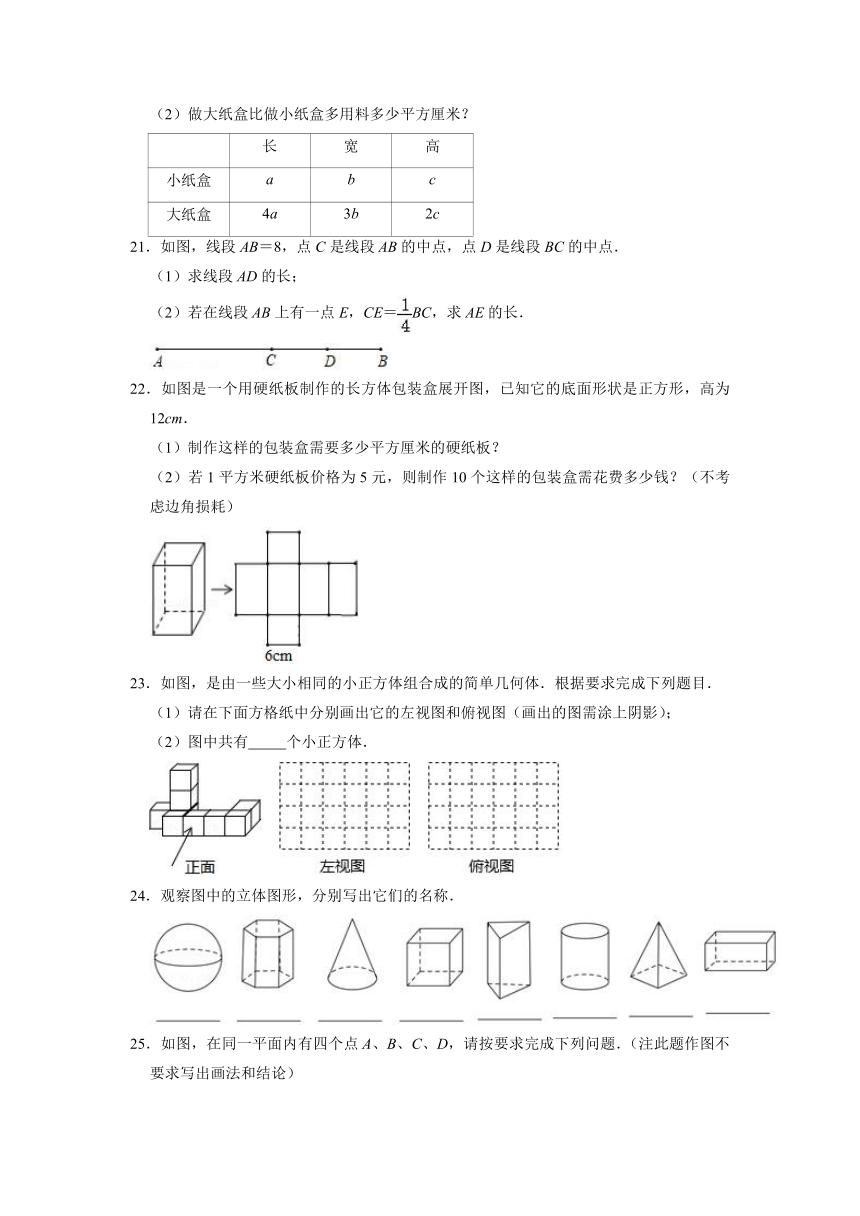
10.如图,下列图形从正面看是三角形的是( )
A. B. C. D.
二、填空题
11.正方体切去一个块,可得到如图几何体,这个几何体有 条棱.
12.已知A,B,C三点在同一条直线上,AB=8,BC=6,M,N分别是AB、BC的中点,则线段MN的长是 .
13.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1、2、3、6的小正方形中不能剪去的是 (填编号).
14.如图所示,在一条笔直公路p的两侧,分别有甲、乙两个村庄,现要在公路p上建一个汽车站,使汽车站到甲、乙两村的距离之和最小,你认为汽车站应该建在 处(填A或B或C),理由是 .
15.6.35°= ° ′.
16.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: .
17.一个棱柱有12个顶点,所有侧棱长的和是48cm,则每条侧棱长是 cm.
18.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 .
19.老师用10个1cm×1cm×1cm的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边(1cm)共享,或有一面(1cm×1cm)共享.老师拿出一张3cm×4cm的方格纸(如图②),请小荣将此10个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有 种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
三、解答题
20.做大小两个长方体纸盒,尺寸如下(单位:厘米).
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
长 宽 高
小纸盒 a b c
大纸盒 4a 3b 2c
21.如图,线段AB=8,点C是线段AB的中点,点D是线段BC的中点.
(1)求线段AD的长;
(2)若在线段AB上有一点E,CE=BC,求AE的长.
22.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这样的包装盒需花费多少钱?(不考虑边角损耗)
23.如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目.
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图需涂上阴影);
(2)图中共有 个小正方体.
24.观察图中的立体图形,分别写出它们的名称.
25.如图,在同一平面内有四个点A、B、C、D,请按要求完成下列问题.(注此题作图不要求写出画法和结论)
(1)作射线AC;
(2)作直线BD与射线AC相交于点O;
(3)分别连接AB、AD;
(4)我们容易判断出线段AB+AD与BD的数量关系是 ,理由是 .
26.计算:
20°18′+34°56′﹣12°34′.
27.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如表:
碟子的个数 碟子的高度(单位:cm)
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
(1)当桌子上放有x个碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看若干碟子,得到的三视图如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度.
28.如图是一个正方体盒子的展开图,若展开图折成正方体后相对面上的两个数互为相反数.
(1)分别求出x、y、z的值,
(2)求x+y﹣z的倒数,
29.如图,这是一个由小立方块搭成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面和从左面看到的形状图.
2020年华东师大新版七年级(上)《第4章 图形的初步认识》常考题套卷(3)
参考答案与试题解析
一、选择题
1.将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )
A.
B.
C.
D.
【解答】解:A、∠α与∠β不互余,故本选项错误;
B、∠α与∠β不互余,故本选项错误;
C、∠α与∠β互余,故本选项正确;
D、∠α与∠β不互余,∠α和∠β互补,故本选项错误;
故选:C.
2.如图,观察图形,下列结论中不正确的是( )
A.直线BA和直线AB是同一条直线
B.图中有5条线段
C.AB+BD>AD
D.射线AC和射线AD是同一条射线
【解答】解:A、直线BA和直线AB是同一条直线,正确;
B、图中有6条线段,故错误;
C、AB+BD>AD,正确;
D、射线AC和射线AD是同一条射线,正确;
故选:B.
3.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm B.3cm C.7cm或3cm D.5cm
【解答】解:(1)当点C在线段AB上时,则MN=AC+BC=AB=5cm;
(2)当点C在线段AB的延长线上时,则MN=AC﹣BC=7﹣2=5cm.
综合上述情况,线段MN的长度是5cm.
故选:D.
4.如下图,将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是( )
A. B.
C. D.
【解答】解:将直角三角形绕较长直角边所在直线旋转一周后形成的几何体为:
将直角三角形绕较短直角边所在直线旋转一周后形成的几何体为:
将直角三角形绕斜边所在直线旋转一周后形成的几何体为:
故选:C.
5.如图所示的沙漏,可以看作是由下列所给的哪个平面图形绕虚线旋转一周而成的( )
A. B. C. D.
【解答】解:由图可知,只有D选项图形绕直线l旋转一周得到如图所示立体图形,
故选:D.
6.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )
A. B.
C. D.
【解答】解:能用∠1、∠AOB、∠O三种方法表示同一个角的图形是C选项中的图,
A,B,D选项中的图都不能同时用∠1、∠AOB、∠O三种方法表示同一个角,
故选:C.
7.某人在点A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,则∠BAC的度数为( )
A.65° B.75° C.40° D.35°
【解答】解:如图所示:
∵某人在A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,
∴∠BAD=40°,∠CAD=35°,
∴∠BAC=∠BAD+∠CAD=40°+35°=75°.
故选:B.
8.已知一个不透明的正方体的六个面上分别写着1﹣6六个数字,如图是我们能看到的三种情况,那么数字5的对面的数字是( )
A.6 B.4 C.3 D.6或4或3
【解答】解:第一个正方体已知1,2,5,第二个正方体已知1,2,4,第三个正方体已知1,4,6,且不同的面上写的数字各不相同,
可求得第一个正方体底面的数字为3,
∴4相邻的数字是1,2,3,6,
∴数字5的对面的数字是4.
故选:B.
9.如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,若组成这个几何体的小正方体的个数为n,则n的最大值为( )
A.9 B.10 C.12 D.14
【解答】解:由题中所给出的主视图知物体共3列,且都是最高两层;由左视图知共三行,所以小正方体的个数最多的几何体为:第一列4个小正方体,第二列3个小正方体,第三列3个小正方体,n的最大值:4+3+3=10个.
故选:B.
10.如图,下列图形从正面看是三角形的是( )
A. B. C. D.
【解答】解:A、三棱柱从正面看到的是长方形,不合题意;
B、圆台从正面看到的是梯形,不合题意;
C、圆锥从正面看到的是三角形,符合题意;
D、长方体从正面看到的是长方形,不合题意.
故选:C.
二、填空题
11.正方体切去一个块,可得到如图几何体,这个几何体有 12 条棱.
【解答】如图,把正方体截去一个角后得到的几何体有12条棱.
故答案为:12.
12.已知A,B,C三点在同一条直线上,AB=8,BC=6,M,N分别是AB、BC的中点,则线段MN的长是 7或1 .
【解答】解:由AB=8,BC=6,M、N分别为AB、BC中点,得
MB=AB=4,NB=BC=3.
①C在线段AB的延长线上,MN=MB+NB=4+3=7;
②C在线段AB上,MN=MB﹣NB=4﹣3=1;
③C在线段AB的反延长线上,AB>BC,不成立,
综上所述:线段MN的长7或1.
故答案为7或1.
13.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1、2、3、6的小正方形中不能剪去的是 3 (填编号).
【解答】解:由图可得,3的唯一对面是5,而4的对面是2或6,7的对面是1或2,
所以将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,编号为1、2、3、6的小正方形中不能剪去的是3,
故答案为:3.
14.如图所示,在一条笔直公路p的两侧,分别有甲、乙两个村庄,现要在公路p上建一个汽车站,使汽车站到甲、乙两村的距离之和最小,你认为汽车站应该建在 处(填A或B或C),理由是 两点之间线段最短 .
【解答】解:汽车站应该建在B处,理由是两点之间线段最短.
故答案为:B;两点之间线段最短.
15.6.35°= 6 ° 21 ′.
【解答】解:0.35°=(0.35×60)′=21′,
即6.35°=6°21′.
故答案为:6,21.
16.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: 两点确定一条直线 .
【解答】解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
17.一个棱柱有12个顶点,所有侧棱长的和是48cm,则每条侧棱长是 8 cm.
【解答】解:根据以上分析一个棱柱有12个顶点,所以它是六棱柱,即有6条侧棱,又因为所有侧棱长的和是48cm,所以每条侧棱长是48÷6=8cm.
故答案为8.
18.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 我 .
【解答】解:由图1可得,“中”和“的”相对;“国”和“我”相对;“梦”和“梦”相对;
由图2可得,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格时,“国”在下面,则这时小正方体朝上一面的字是“我”.
故答案为:我.
19.老师用10个1cm×1cm×1cm的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边(1cm)共享,或有一面(1cm×1cm)共享.老师拿出一张3cm×4cm的方格纸(如图②),请小荣将此10个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有 16 种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
【解答】解:由题意可知,立体图形只有一排左视图有3个正方形,有两到三排.
三排的左视图有:3×4=12种;
两排的左视图有:2×2=4种;
共12+4=16种.
故答案为:16.
三、解答题
20.做大小两个长方体纸盒,尺寸如下(单位:厘米).
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
长 宽 高
小纸盒 a b c
大纸盒 4a 3b 2c
【解答】解:(1)做这两个纸盒共用料:
(2ab+2bc+2ac)+(12ab+8ac+6bc)×2,
=2ab+2bc+2ac+24ab+16ac+12bc
=26ab+14bc+18ac(cm2);
∴做这两个纸盒共用料(26ab+14bc+18ac)平方厘米;
(2)做大纸盒比做小纸盒多用料:
2×(12ab+8ac+6bc)﹣(2ab+2bc+2ac)=24ab+12bc+16ac﹣2ab﹣2bc﹣2ac
=22ab+10bc+14ac(cm2);
∴做大纸盒比做小纸盒多用料(22ab+10bc+14ac)平方厘米.
21.如图,线段AB=8,点C是线段AB的中点,点D是线段BC的中点.
(1)求线段AD的长;
(2)若在线段AB上有一点E,CE=BC,求AE的长.
【解答】解:(1)∵AB=8,C是AB的中点,
∴AC=BC=4,
∵D是BC的中点,
∴CD=BC=2,
∴AD=AC+CD=6;
(2)∵BC=4,CE=BC,
∴CE=×4=1,
当E在C的左边时,AE=AC﹣CE=4﹣1=3;
当E在C的右边时,AE=AC+CE=4+1=5.
∴AE的长为3或5.
22.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这样的包装盒需花费多少钱?(不考虑边角损耗)
【解答】解:(1)由题意得,2×(12×6+12×6+6×6)=360cm2;
答:制作这样的包装盒需要360平方厘米的硬纸板;
(2)360÷10000×5×10=1.8元,
答:制作10个这样的包装盒需花费1.8元钱.
23.如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目.
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图需涂上阴影);
(2)图中共有 9 个小正方体.
【解答】解:(1)如图所示:
;
(2)图中共有9个小正方体.
故答案为:9.
24.观察图中的立体图形,分别写出它们的名称.
【解答】解:它们的名称分别为:球体,直六棱柱,圆锥体,正方体,直三棱柱,圆柱体,四棱锥,长方体.
25.如图,在同一平面内有四个点A、B、C、D,请按要求完成下列问题.(注此题作图不要求写出画法和结论)
(1)作射线AC;
(2)作直线BD与射线AC相交于点O;
(3)分别连接AB、AD;
(4)我们容易判断出线段AB+AD与BD的数量关系是 AB+AD>BD ,理由是 两点之间,线段最短 .
【解答】解:(1)(2)(3)如图所示:
(4)AB+AD>BD,理由是:两点之间,线段最短.
故答案为:AB+AD>BD,两点之间线段最短.
26.计算:
20°18′+34°56′﹣12°34′.
【解答】解:20°18′+34°56′﹣12°34′
=55°14′﹣12°34′
=42°40′.
27.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如表:
碟子的个数 碟子的高度(单位:cm)
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
(1)当桌子上放有x个碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看若干碟子,得到的三视图如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度.
【解答】解:(1)由题意得:2+1.5(x﹣1)=1.5x+0.5;
(2)由三视图可知共有15个碟子,
∴叠成一摞的高度=1.5×15+0.5=23(cm),
答:叠成一摞后的高度为23cm.
28.如图是一个正方体盒子的展开图,若展开图折成正方体后相对面上的两个数互为相反数.
(1)分别求出x、y、z的值,
(2)求x+y﹣z的倒数,
【解答】解:(1)正方体的表面展开图,相对的面之间一定相隔一个正方形,
“x”与“0”是相对面,
“y”与“﹣20”是相对面,
“z”与“18”是相对面,
∵折成正方体后相对面上的两个数互为相反数,
∴x=0,y=20,z=﹣18;
(2)∴x+y﹣z=0+20+18=38,
∴x+y﹣z的倒数是.
29.如图,这是一个由小立方块搭成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面和从左面看到的形状图.
【解答】解:如图所示:
一、选择题
1.将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )
A.
B.
C.
D.
2.如图,观察图形,下列结论中不正确的是( )
A.直线BA和直线AB是同一条直线
B.图中有5条线段
C.AB+BD>AD
D.射线AC和射线AD是同一条射线
3.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm B.3cm C.7cm或3cm D.5cm
4.如下图,将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是( )
A. B.
C. D.
5.如图所示的沙漏,可以看作是由下列所给的哪个平面图形绕虚线旋转一周而成的( )
A. B. C. D.
6.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )
A. B.
C. D.
7.某人在点A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,则∠BAC的度数为( )
A.65° B.75° C.40° D.35°
8.已知一个不透明的正方体的六个面上分别写着1﹣6六个数字,如图是我们能看到的三种情况,那么数字5的对面的数字是( )
A.6 B.4 C.3 D.6或4或3
9.如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,若组成这个几何体的小正方体的个数为n,则n的最大值为( )
A.9 B.10 C.12 D.14
10.如图,下列图形从正面看是三角形的是( )
A. B. C. D.
二、填空题
11.正方体切去一个块,可得到如图几何体,这个几何体有 条棱.
12.已知A,B,C三点在同一条直线上,AB=8,BC=6,M,N分别是AB、BC的中点,则线段MN的长是 .
13.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1、2、3、6的小正方形中不能剪去的是 (填编号).
14.如图所示,在一条笔直公路p的两侧,分别有甲、乙两个村庄,现要在公路p上建一个汽车站,使汽车站到甲、乙两村的距离之和最小,你认为汽车站应该建在 处(填A或B或C),理由是 .
15.6.35°= ° ′.
16.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: .
17.一个棱柱有12个顶点,所有侧棱长的和是48cm,则每条侧棱长是 cm.
18.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 .
19.老师用10个1cm×1cm×1cm的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边(1cm)共享,或有一面(1cm×1cm)共享.老师拿出一张3cm×4cm的方格纸(如图②),请小荣将此10个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有 种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
三、解答题
20.做大小两个长方体纸盒,尺寸如下(单位:厘米).
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
长 宽 高
小纸盒 a b c
大纸盒 4a 3b 2c
21.如图,线段AB=8,点C是线段AB的中点,点D是线段BC的中点.
(1)求线段AD的长;
(2)若在线段AB上有一点E,CE=BC,求AE的长.
22.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这样的包装盒需花费多少钱?(不考虑边角损耗)
23.如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目.
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图需涂上阴影);
(2)图中共有 个小正方体.
24.观察图中的立体图形,分别写出它们的名称.
25.如图,在同一平面内有四个点A、B、C、D,请按要求完成下列问题.(注此题作图不要求写出画法和结论)
(1)作射线AC;
(2)作直线BD与射线AC相交于点O;
(3)分别连接AB、AD;
(4)我们容易判断出线段AB+AD与BD的数量关系是 ,理由是 .
26.计算:
20°18′+34°56′﹣12°34′.
27.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如表:
碟子的个数 碟子的高度(单位:cm)
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
(1)当桌子上放有x个碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看若干碟子,得到的三视图如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度.
28.如图是一个正方体盒子的展开图,若展开图折成正方体后相对面上的两个数互为相反数.
(1)分别求出x、y、z的值,
(2)求x+y﹣z的倒数,
29.如图,这是一个由小立方块搭成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面和从左面看到的形状图.
2020年华东师大新版七年级(上)《第4章 图形的初步认识》常考题套卷(3)
参考答案与试题解析
一、选择题
1.将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )
A.
B.
C.
D.
【解答】解:A、∠α与∠β不互余,故本选项错误;
B、∠α与∠β不互余,故本选项错误;
C、∠α与∠β互余,故本选项正确;
D、∠α与∠β不互余,∠α和∠β互补,故本选项错误;
故选:C.
2.如图,观察图形,下列结论中不正确的是( )
A.直线BA和直线AB是同一条直线
B.图中有5条线段
C.AB+BD>AD
D.射线AC和射线AD是同一条射线
【解答】解:A、直线BA和直线AB是同一条直线,正确;
B、图中有6条线段,故错误;
C、AB+BD>AD,正确;
D、射线AC和射线AD是同一条射线,正确;
故选:B.
3.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm B.3cm C.7cm或3cm D.5cm
【解答】解:(1)当点C在线段AB上时,则MN=AC+BC=AB=5cm;
(2)当点C在线段AB的延长线上时,则MN=AC﹣BC=7﹣2=5cm.
综合上述情况,线段MN的长度是5cm.
故选:D.
4.如下图,将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是( )
A. B.
C. D.
【解答】解:将直角三角形绕较长直角边所在直线旋转一周后形成的几何体为:
将直角三角形绕较短直角边所在直线旋转一周后形成的几何体为:
将直角三角形绕斜边所在直线旋转一周后形成的几何体为:
故选:C.
5.如图所示的沙漏,可以看作是由下列所给的哪个平面图形绕虚线旋转一周而成的( )
A. B. C. D.
【解答】解:由图可知,只有D选项图形绕直线l旋转一周得到如图所示立体图形,
故选:D.
6.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )
A. B.
C. D.
【解答】解:能用∠1、∠AOB、∠O三种方法表示同一个角的图形是C选项中的图,
A,B,D选项中的图都不能同时用∠1、∠AOB、∠O三种方法表示同一个角,
故选:C.
7.某人在点A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,则∠BAC的度数为( )
A.65° B.75° C.40° D.35°
【解答】解:如图所示:
∵某人在A处看点B在北偏东40°的方向上,看点C在北偏西35°的方向上,
∴∠BAD=40°,∠CAD=35°,
∴∠BAC=∠BAD+∠CAD=40°+35°=75°.
故选:B.
8.已知一个不透明的正方体的六个面上分别写着1﹣6六个数字,如图是我们能看到的三种情况,那么数字5的对面的数字是( )
A.6 B.4 C.3 D.6或4或3
【解答】解:第一个正方体已知1,2,5,第二个正方体已知1,2,4,第三个正方体已知1,4,6,且不同的面上写的数字各不相同,
可求得第一个正方体底面的数字为3,
∴4相邻的数字是1,2,3,6,
∴数字5的对面的数字是4.
故选:B.
9.如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,若组成这个几何体的小正方体的个数为n,则n的最大值为( )
A.9 B.10 C.12 D.14
【解答】解:由题中所给出的主视图知物体共3列,且都是最高两层;由左视图知共三行,所以小正方体的个数最多的几何体为:第一列4个小正方体,第二列3个小正方体,第三列3个小正方体,n的最大值:4+3+3=10个.
故选:B.
10.如图,下列图形从正面看是三角形的是( )
A. B. C. D.
【解答】解:A、三棱柱从正面看到的是长方形,不合题意;
B、圆台从正面看到的是梯形,不合题意;
C、圆锥从正面看到的是三角形,符合题意;
D、长方体从正面看到的是长方形,不合题意.
故选:C.
二、填空题
11.正方体切去一个块,可得到如图几何体,这个几何体有 12 条棱.
【解答】如图,把正方体截去一个角后得到的几何体有12条棱.
故答案为:12.
12.已知A,B,C三点在同一条直线上,AB=8,BC=6,M,N分别是AB、BC的中点,则线段MN的长是 7或1 .
【解答】解:由AB=8,BC=6,M、N分别为AB、BC中点,得
MB=AB=4,NB=BC=3.
①C在线段AB的延长线上,MN=MB+NB=4+3=7;
②C在线段AB上,MN=MB﹣NB=4﹣3=1;
③C在线段AB的反延长线上,AB>BC,不成立,
综上所述:线段MN的长7或1.
故答案为7或1.
13.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1、2、3、6的小正方形中不能剪去的是 3 (填编号).
【解答】解:由图可得,3的唯一对面是5,而4的对面是2或6,7的对面是1或2,
所以将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,编号为1、2、3、6的小正方形中不能剪去的是3,
故答案为:3.
14.如图所示,在一条笔直公路p的两侧,分别有甲、乙两个村庄,现要在公路p上建一个汽车站,使汽车站到甲、乙两村的距离之和最小,你认为汽车站应该建在 处(填A或B或C),理由是 两点之间线段最短 .
【解答】解:汽车站应该建在B处,理由是两点之间线段最短.
故答案为:B;两点之间线段最短.
15.6.35°= 6 ° 21 ′.
【解答】解:0.35°=(0.35×60)′=21′,
即6.35°=6°21′.
故答案为:6,21.
16.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: 两点确定一条直线 .
【解答】解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
17.一个棱柱有12个顶点,所有侧棱长的和是48cm,则每条侧棱长是 8 cm.
【解答】解:根据以上分析一个棱柱有12个顶点,所以它是六棱柱,即有6条侧棱,又因为所有侧棱长的和是48cm,所以每条侧棱长是48÷6=8cm.
故答案为8.
18.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 我 .
【解答】解:由图1可得,“中”和“的”相对;“国”和“我”相对;“梦”和“梦”相对;
由图2可得,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格时,“国”在下面,则这时小正方体朝上一面的字是“我”.
故答案为:我.
19.老师用10个1cm×1cm×1cm的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边(1cm)共享,或有一面(1cm×1cm)共享.老师拿出一张3cm×4cm的方格纸(如图②),请小荣将此10个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有 16 种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
【解答】解:由题意可知,立体图形只有一排左视图有3个正方形,有两到三排.
三排的左视图有:3×4=12种;
两排的左视图有:2×2=4种;
共12+4=16种.
故答案为:16.
三、解答题
20.做大小两个长方体纸盒,尺寸如下(单位:厘米).
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
长 宽 高
小纸盒 a b c
大纸盒 4a 3b 2c
【解答】解:(1)做这两个纸盒共用料:
(2ab+2bc+2ac)+(12ab+8ac+6bc)×2,
=2ab+2bc+2ac+24ab+16ac+12bc
=26ab+14bc+18ac(cm2);
∴做这两个纸盒共用料(26ab+14bc+18ac)平方厘米;
(2)做大纸盒比做小纸盒多用料:
2×(12ab+8ac+6bc)﹣(2ab+2bc+2ac)=24ab+12bc+16ac﹣2ab﹣2bc﹣2ac
=22ab+10bc+14ac(cm2);
∴做大纸盒比做小纸盒多用料(22ab+10bc+14ac)平方厘米.
21.如图,线段AB=8,点C是线段AB的中点,点D是线段BC的中点.
(1)求线段AD的长;
(2)若在线段AB上有一点E,CE=BC,求AE的长.
【解答】解:(1)∵AB=8,C是AB的中点,
∴AC=BC=4,
∵D是BC的中点,
∴CD=BC=2,
∴AD=AC+CD=6;
(2)∵BC=4,CE=BC,
∴CE=×4=1,
当E在C的左边时,AE=AC﹣CE=4﹣1=3;
当E在C的右边时,AE=AC+CE=4+1=5.
∴AE的长为3或5.
22.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这样的包装盒需花费多少钱?(不考虑边角损耗)
【解答】解:(1)由题意得,2×(12×6+12×6+6×6)=360cm2;
答:制作这样的包装盒需要360平方厘米的硬纸板;
(2)360÷10000×5×10=1.8元,
答:制作10个这样的包装盒需花费1.8元钱.
23.如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目.
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图需涂上阴影);
(2)图中共有 9 个小正方体.
【解答】解:(1)如图所示:
;
(2)图中共有9个小正方体.
故答案为:9.
24.观察图中的立体图形,分别写出它们的名称.
【解答】解:它们的名称分别为:球体,直六棱柱,圆锥体,正方体,直三棱柱,圆柱体,四棱锥,长方体.
25.如图,在同一平面内有四个点A、B、C、D,请按要求完成下列问题.(注此题作图不要求写出画法和结论)
(1)作射线AC;
(2)作直线BD与射线AC相交于点O;
(3)分别连接AB、AD;
(4)我们容易判断出线段AB+AD与BD的数量关系是 AB+AD>BD ,理由是 两点之间,线段最短 .
【解答】解:(1)(2)(3)如图所示:
(4)AB+AD>BD,理由是:两点之间,线段最短.
故答案为:AB+AD>BD,两点之间线段最短.
26.计算:
20°18′+34°56′﹣12°34′.
【解答】解:20°18′+34°56′﹣12°34′
=55°14′﹣12°34′
=42°40′.
27.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如表:
碟子的个数 碟子的高度(单位:cm)
1 2
2 2+1.5
3 2+3
4 2+4.5
… …
(1)当桌子上放有x个碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看若干碟子,得到的三视图如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度.
【解答】解:(1)由题意得:2+1.5(x﹣1)=1.5x+0.5;
(2)由三视图可知共有15个碟子,
∴叠成一摞的高度=1.5×15+0.5=23(cm),
答:叠成一摞后的高度为23cm.
28.如图是一个正方体盒子的展开图,若展开图折成正方体后相对面上的两个数互为相反数.
(1)分别求出x、y、z的值,
(2)求x+y﹣z的倒数,
【解答】解:(1)正方体的表面展开图,相对的面之间一定相隔一个正方形,
“x”与“0”是相对面,
“y”与“﹣20”是相对面,
“z”与“18”是相对面,
∵折成正方体后相对面上的两个数互为相反数,
∴x=0,y=20,z=﹣18;
(2)∴x+y﹣z=0+20+18=38,
∴x+y﹣z的倒数是.
29.如图,这是一个由小立方块搭成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面和从左面看到的形状图.
【解答】解:如图所示:
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
