23.3.3 相似三角形的性质 同步练习 2021-2022学年华东师大版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 23.3.3 相似三角形的性质 同步练习 2021-2022学年华东师大版九年级数学上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 751.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-04 10:03:51 | ||
图片预览


文档简介
相似三角形的性质
一、单选题
1.△ADE∽△ABC,若AD=1,AB=4,则△ADE与△ABC的相似比是( )
A.1:2 B.1:3 C.2:3 D.1:4
2.如图,,且与的面积分别是和,与的周长分别是和,则一定成立的等式是( )
A. B. C. D.
3.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=9:49,则DE:DC=( )
A.2:5 B.2:3 C.3:7 D.3:4
4.如图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面直径AB的长度是( )
A.2cm B.2.5cm C.3cm D.4cm
5.△ABC的三边长分别为7,6,2,△DEF的两边长分别为1,3,要使△ABC∽△DEF,则△DEF的第三边长应为( )
A. B.2 C. D.
6.如图,在中,点E是AB上任意一点,过点E作EFBC交CD于点F,连接AF并延长交BC的延长线于点H,则下列结论中错误的是( )
A. B. C. D.
7.如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度( )
A.12米 B.14米 C.16米 D.18米
8.如图,已知A、B是反比例函数y=图象上两点,连接AB并延长,交y轴于C.若AB∶BC=3∶1,S△AOC=10,则k的值为( )
A.2 B.﹣2 C.4 D.﹣4
9.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论:①∠BAE=30°;②CE2=AB·CF;③CF=CD;④△ABE∽△AEF.正确的有( ).
A.1个 B.2个 C.3个 D.4个
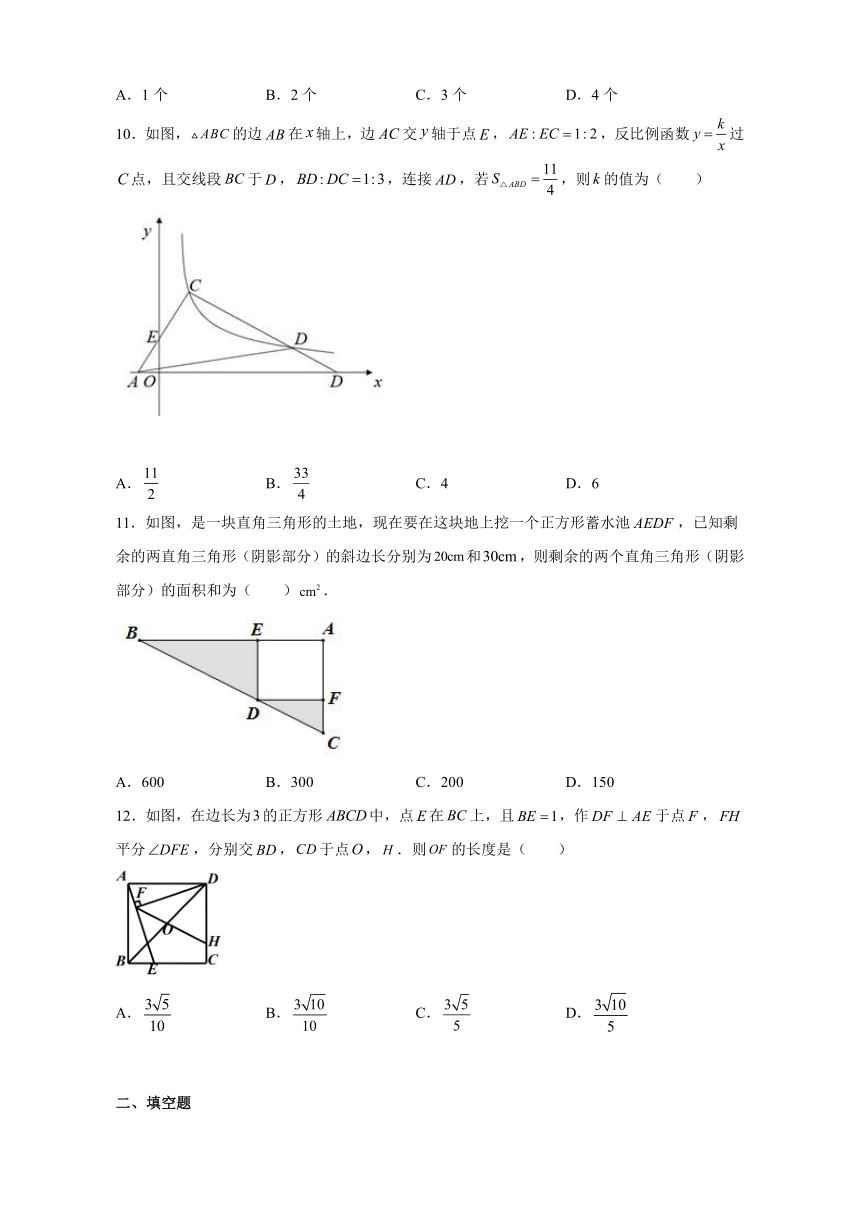
10.如图,的边在轴上,边交轴于点,,反比例函数过点,且交线段于,,连接,若,则的值为( )
A. B. C.4 D.6
11.如图,是一块直角三角形的土地,现在要在这块地上挖一个正方形蓄水池,已知剩余的两直角三角形(阴影部分)的斜边长分别为和,则剩余的两个直角三角形(阴影部分)的面积和为( ).
A.600 B.300 C.200 D.150
12.如图,在边长为的正方形中,点在上,且,作于点,平分,分别交,于点,.则的长度是( )
A. B. C. D.
二、填空题
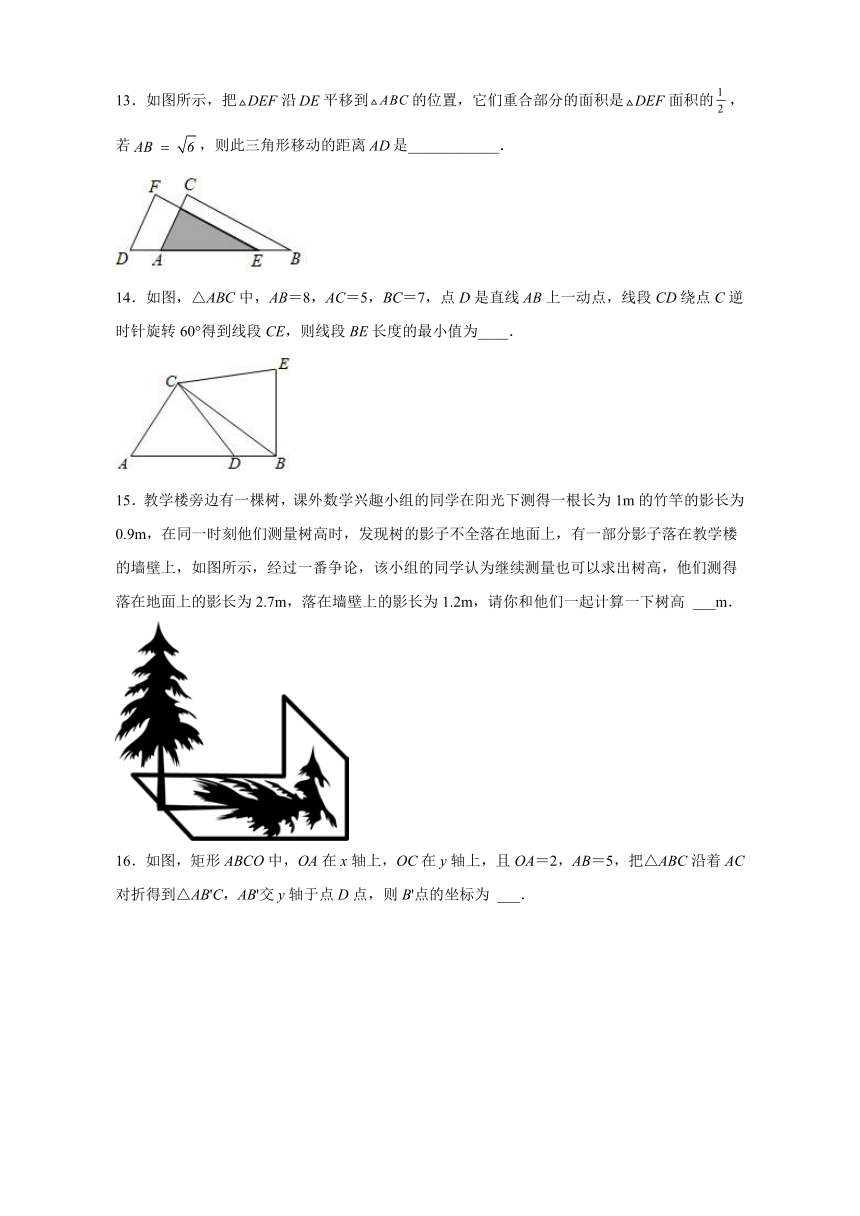
13.如图所示,把沿平移到的位置,它们重合部分的面积是面积的,若,则此三角形移动的距离是____________.
14.如图,△ABC中,AB=8,AC=5,BC=7,点D是直线AB上一动点,线段CD绕点C逆时针旋转60°得到线段CE,则线段BE长度的最小值为____.
15.教学楼旁边有一棵树,课外数学兴趣小组的同学在阳光下测得一根长为1m的竹竿的影长为0.9m,在同一时刻他们测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图所示,经过一番争论,该小组的同学认为继续测量也可以求出树高,他们测得落在地面上的影长为2.7m,落在墙壁上的影长为1.2m,请你和他们一起计算一下树高 ___m.
16.如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB'C,AB'交y轴于点D点,则B'点的坐标为 ___.
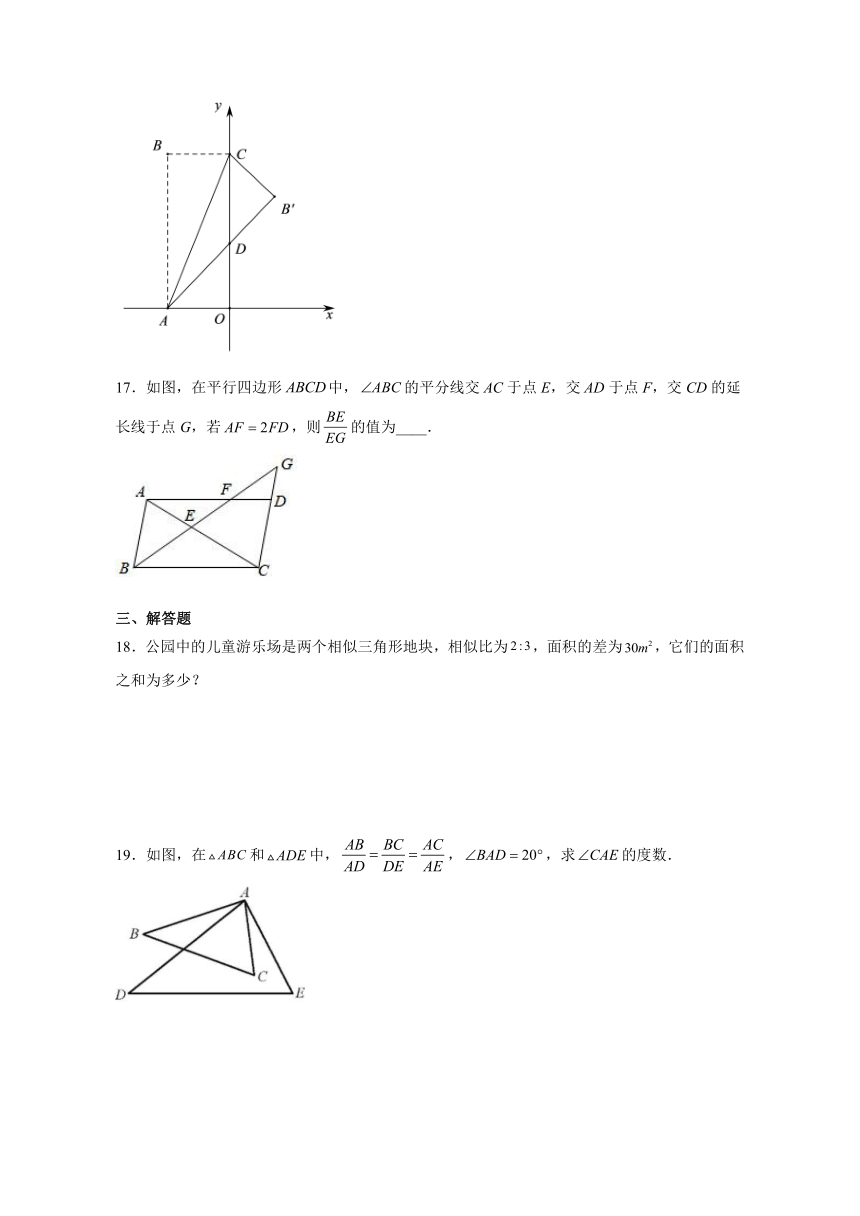
17.如图,在平行四边形中,的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若,则的值为____.
三、解答题
18.公园中的儿童游乐场是两个相似三角形地块,相似比为,面积的差为,它们的面积之和为多少?
19.如图,在和中,,,求的度数.
20.如图,四边形和四边形都是平行四边形,点R为的中点,分别交和于点P,Q,求.
21.如图,在中,对角线与相交于点O,E是延长线上的一点,连接交于点F.已知,求的长.
22.如图,点D,E分别是和上的点,,,.
(1)求的度数;
(2)求的度数;
(3)求的长.
参考答案
1.D
解:∵△ADE∽△ABC,
∴△ADE与△ABC的相似比为AD:AB=1:4.
故选:D.
2.D
解:∵△OAB∽△OCD,OA:OC=6:5,
∴,
∴选项D正确,选项C错误,
∵无法确定和∠ A与∠B的比的值,故选项A,B错误,
故选:D.
3.C
解:四边形是平行四边形,
,
,,
,
,
,
,
.
故选:C.
4.C
解:如图:过O作OM⊥CD,垂足为M,过O作ON⊥AB,垂足为N,
∵CD∥AB,
∴△CDO∽ABO,即相似比为,
∴,
∵OM=15-7=8(cm),ON=11-7=4(cm),
∴,
∴AB=3cm,
故选:C.
5.C
解:△ABC∽△DEF
△ABC的三边长分别为7,6,2,△DEF的两边长分别为1,3,
设△DEF的第三边长为,
则,
解得.
故选C.
6.D
解:∵四边形ABCD为平行四边形,EFBC,
∴AD=EF=BC,AE=DF,BE=CF.
A、∵ADCH,
∴△ADF∽△HCF,
∴,即,结论A正确;
B、∵ABCD,
∴△ABH∽△FCH,
∴,即,结论B正确;
C、∵ADBH,
∴△ADF∽△HBA,
∴,即,结论C正确;
D、∵AECF,EFCH,
∴△FCH∽△AEF,
∴,即,结论D错误.
故选:D.
7.C
解:如下图:
过点C作CE⊥AB于点E,某一时刻竹竿和影长构成的三角形为△FGH,此时FG=1米,GH=1.5米,BD=EC=21米,CD=EB=2米.
据题意,同一时刻,
∴
∴
∴AE=14
∴AB=AE+BE=14+2=16米
故选:C
8.D
解:作AM∥x轴交y轴于M,BN∥x轴交y轴于N,
∴AM∥BN,
∴==,
设B(m,),
∴BN=﹣m,ON=,
∵AB:BC=3:1,
∴=,
∴AM=4BN=﹣4m,
∴A(4m,),
∵S△AOC=OC AM=10,
∴OC=﹣,
∴CN=OC﹣ON=﹣﹣=﹣,MC=﹣﹣=﹣,
∵=,即=,
解得k=﹣4
故选:D.
9.B
解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,
∵AE⊥EF,
∴∠AEF=∠B=90°,
∴∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠CEF,
∴,
∴,即,
∴,故②正确;
∵E是BC的中点,
∴,
∴,
∴,故①错误;
∴,故③错误;
设CF=a,则BE=CE=2a,AB=CD=AD=4a,DF=3a,
∴,,AF=5a,
∴,
,
∴,
∴,故④正确.
∴②与④正确.
∴正确结论的个数有2个.
故选:B.
10.C
解:过C点作CN⊥y轴于N点,过C点作CE⊥x轴于E点,过D点作DF⊥x轴于F点,
设CN=2a,则OE=2a
∵CNAE
∴△AOE∽△CNE,
∴
∴AO=a
∵C点在函数上
∴C(2a,)
∴CE=NO=
∵CEDF
∴△BDF∽△BCE,
∵
∴
∴DF=,
∵D点在函数上
∴D点坐标为(8a,)
∴EF=8a-2a=6a
∵
∴BF=2a
∴B(10a,0)
∴AB=11a
∵
∴
解得k=4
故选C.
11.B
解:设DE=xcm,BE=ycm,
∵∠B+∠C=90°, ∠FDC+∠C=90°,
∴∠B=∠FDC,
又∠BED=∠DFC,
∴△BED∽△DFC,
∴,
∴DF=y,CF=x,
∵DE=DF,
∴x=y,
∵在Rt△BED中,BE2+DE2=BD2,
∴y2+x2=900,
联立两个方程,解得:y2=,
∴阴影部分的面积=xy+×xy=y2=300cm2
故选B.
12.C
解:如图,和交与点,过作交于,过点作交于,
,
,
,
又,,
,
,,
设,
∵,
则,
解得,
,
,
设,则,
解得,
,
故选:C.
13.
解:如图,
∵把△DEF沿DE边平移到△ABC的位置,
∴AC∥DF,
∴△DEF∽△GAE,
∵S△DEF:S△GAE=2,
∴DE:AE=,
∵,
∴
∴AE=,
∴DA=.
故答案为:.
14.
解:如图,以BC为边作等边△BCT,过点T作TH⊥AB于H,过点C作CK⊥AB于K,设CT交AB于点J.
∵∠ECD=∠BCT=60°,
∴∠ECB=∠DCT,
∵CE=CD,CB=CT,
∴△ECB≌△DCT(SAS),
∴BE=DT,
∴当点D与H重合时,DT的值最小,此时BE的值最小,最小值=TH的长,
∵CK⊥AB,
∴CK2=AC2-AK2=BC2-BK2,
∴52-AK2=72-(8-AK)2,
∴AK=,
∴AC=2AK,
∴∠ACK=30°,∠A=60°,CK=AK=,
∵∠BCJ=∠A=60°,∠CBJ=∠ABC,
∴△BCJ∽△BAC,
∴,
∴BJ,
∵BK=AB-AK=,
∴,
∴,
∴,
∵TH⊥AB,CK⊥AB,
∴TH∥CK,
∴,
∴,
∴TH=,
∴BE的最小值为.
15.##
解:如图,过点C作CE∥AD,交AB于E,
∴四边形AECD是平行四边形,
∴AE=CD.
由题意,得△EBC∽△PQR,
∴,即.
∴BE=3m.
∴AB=BE+AE=3+1.2=4.2(m).
即树高为4.2m.
故答案为:4.2.
16.
解:过点作轴于点,如图,
折叠,OA=2,AB=5,
,,
四边形是矩形,
,
,
,
,
设,则,
在中,
,
即,
解得,
,
,
轴,轴,
,
,
,
即,
解得,
,
.
故答案为:.
17.
解:设,
∵,
∴,,
∵四边形是平行四边形,
∴,,,
∴,,
∵平分,
∴,
∴,
∴,,
∴,
∵,
∴,
∴,
∴,
故答案为:.
18..
解:∵两三角形的相似比为,
∴它们的面积比为,
设较小三角形的面积为,则较大三角形的面积为,
则,
解得,
∴面积和为,
答:它们的面积和为.
19.
解:在和中,,
,
,
,
.
20..
解:∵ACDE,
∴△PBC∽△RBE,
∴,
∴BP=PR,
又∵△PCQ∽△RDQ,
∴,
∴QR=2PQ,
∴BP:PQ:QR=3:1:2.
21..
解:过点O作OMAB,交BC于点M,
四边形ABCD是平行四边形
,
.
22.(1);(2);(3).
解:(1)∵,,
∴;
(2)在△ADE中,
;
(3)∵,
∴,
∵,
∴,
∴,
∴.
一、单选题
1.△ADE∽△ABC,若AD=1,AB=4,则△ADE与△ABC的相似比是( )
A.1:2 B.1:3 C.2:3 D.1:4
2.如图,,且与的面积分别是和,与的周长分别是和,则一定成立的等式是( )
A. B. C. D.
3.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=9:49,则DE:DC=( )
A.2:5 B.2:3 C.3:7 D.3:4
4.如图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面直径AB的长度是( )
A.2cm B.2.5cm C.3cm D.4cm
5.△ABC的三边长分别为7,6,2,△DEF的两边长分别为1,3,要使△ABC∽△DEF,则△DEF的第三边长应为( )
A. B.2 C. D.
6.如图,在中,点E是AB上任意一点,过点E作EFBC交CD于点F,连接AF并延长交BC的延长线于点H,则下列结论中错误的是( )
A. B. C. D.
7.如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度( )
A.12米 B.14米 C.16米 D.18米
8.如图,已知A、B是反比例函数y=图象上两点,连接AB并延长,交y轴于C.若AB∶BC=3∶1,S△AOC=10,则k的值为( )
A.2 B.﹣2 C.4 D.﹣4
9.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论:①∠BAE=30°;②CE2=AB·CF;③CF=CD;④△ABE∽△AEF.正确的有( ).
A.1个 B.2个 C.3个 D.4个
10.如图,的边在轴上,边交轴于点,,反比例函数过点,且交线段于,,连接,若,则的值为( )
A. B. C.4 D.6
11.如图,是一块直角三角形的土地,现在要在这块地上挖一个正方形蓄水池,已知剩余的两直角三角形(阴影部分)的斜边长分别为和,则剩余的两个直角三角形(阴影部分)的面积和为( ).
A.600 B.300 C.200 D.150
12.如图,在边长为的正方形中,点在上,且,作于点,平分,分别交,于点,.则的长度是( )
A. B. C. D.
二、填空题
13.如图所示,把沿平移到的位置,它们重合部分的面积是面积的,若,则此三角形移动的距离是____________.
14.如图,△ABC中,AB=8,AC=5,BC=7,点D是直线AB上一动点,线段CD绕点C逆时针旋转60°得到线段CE,则线段BE长度的最小值为____.
15.教学楼旁边有一棵树,课外数学兴趣小组的同学在阳光下测得一根长为1m的竹竿的影长为0.9m,在同一时刻他们测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图所示,经过一番争论,该小组的同学认为继续测量也可以求出树高,他们测得落在地面上的影长为2.7m,落在墙壁上的影长为1.2m,请你和他们一起计算一下树高 ___m.
16.如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB'C,AB'交y轴于点D点,则B'点的坐标为 ___.
17.如图,在平行四边形中,的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若,则的值为____.
三、解答题
18.公园中的儿童游乐场是两个相似三角形地块,相似比为,面积的差为,它们的面积之和为多少?
19.如图,在和中,,,求的度数.
20.如图,四边形和四边形都是平行四边形,点R为的中点,分别交和于点P,Q,求.
21.如图,在中,对角线与相交于点O,E是延长线上的一点,连接交于点F.已知,求的长.
22.如图,点D,E分别是和上的点,,,.
(1)求的度数;
(2)求的度数;
(3)求的长.
参考答案
1.D
解:∵△ADE∽△ABC,
∴△ADE与△ABC的相似比为AD:AB=1:4.
故选:D.
2.D
解:∵△OAB∽△OCD,OA:OC=6:5,
∴,
∴选项D正确,选项C错误,
∵无法确定和∠ A与∠B的比的值,故选项A,B错误,
故选:D.
3.C
解:四边形是平行四边形,
,
,,
,
,
,
,
.
故选:C.
4.C
解:如图:过O作OM⊥CD,垂足为M,过O作ON⊥AB,垂足为N,
∵CD∥AB,
∴△CDO∽ABO,即相似比为,
∴,
∵OM=15-7=8(cm),ON=11-7=4(cm),
∴,
∴AB=3cm,
故选:C.
5.C
解:△ABC∽△DEF
△ABC的三边长分别为7,6,2,△DEF的两边长分别为1,3,
设△DEF的第三边长为,
则,
解得.
故选C.
6.D
解:∵四边形ABCD为平行四边形,EFBC,
∴AD=EF=BC,AE=DF,BE=CF.
A、∵ADCH,
∴△ADF∽△HCF,
∴,即,结论A正确;
B、∵ABCD,
∴△ABH∽△FCH,
∴,即,结论B正确;
C、∵ADBH,
∴△ADF∽△HBA,
∴,即,结论C正确;
D、∵AECF,EFCH,
∴△FCH∽△AEF,
∴,即,结论D错误.
故选:D.
7.C
解:如下图:
过点C作CE⊥AB于点E,某一时刻竹竿和影长构成的三角形为△FGH,此时FG=1米,GH=1.5米,BD=EC=21米,CD=EB=2米.
据题意,同一时刻,
∴
∴
∴AE=14
∴AB=AE+BE=14+2=16米
故选:C
8.D
解:作AM∥x轴交y轴于M,BN∥x轴交y轴于N,
∴AM∥BN,
∴==,
设B(m,),
∴BN=﹣m,ON=,
∵AB:BC=3:1,
∴=,
∴AM=4BN=﹣4m,
∴A(4m,),
∵S△AOC=OC AM=10,
∴OC=﹣,
∴CN=OC﹣ON=﹣﹣=﹣,MC=﹣﹣=﹣,
∵=,即=,
解得k=﹣4
故选:D.
9.B
解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,
∵AE⊥EF,
∴∠AEF=∠B=90°,
∴∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠CEF,
∴,
∴,即,
∴,故②正确;
∵E是BC的中点,
∴,
∴,
∴,故①错误;
∴,故③错误;
设CF=a,则BE=CE=2a,AB=CD=AD=4a,DF=3a,
∴,,AF=5a,
∴,
,
∴,
∴,故④正确.
∴②与④正确.
∴正确结论的个数有2个.
故选:B.
10.C
解:过C点作CN⊥y轴于N点,过C点作CE⊥x轴于E点,过D点作DF⊥x轴于F点,
设CN=2a,则OE=2a
∵CNAE
∴△AOE∽△CNE,
∴
∴AO=a
∵C点在函数上
∴C(2a,)
∴CE=NO=
∵CEDF
∴△BDF∽△BCE,
∵
∴
∴DF=,
∵D点在函数上
∴D点坐标为(8a,)
∴EF=8a-2a=6a
∵
∴BF=2a
∴B(10a,0)
∴AB=11a
∵
∴
解得k=4
故选C.
11.B
解:设DE=xcm,BE=ycm,
∵∠B+∠C=90°, ∠FDC+∠C=90°,
∴∠B=∠FDC,
又∠BED=∠DFC,
∴△BED∽△DFC,
∴,
∴DF=y,CF=x,
∵DE=DF,
∴x=y,
∵在Rt△BED中,BE2+DE2=BD2,
∴y2+x2=900,
联立两个方程,解得:y2=,
∴阴影部分的面积=xy+×xy=y2=300cm2
故选B.
12.C
解:如图,和交与点,过作交于,过点作交于,
,
,
,
又,,
,
,,
设,
∵,
则,
解得,
,
,
设,则,
解得,
,
故选:C.
13.
解:如图,
∵把△DEF沿DE边平移到△ABC的位置,
∴AC∥DF,
∴△DEF∽△GAE,
∵S△DEF:S△GAE=2,
∴DE:AE=,
∵,
∴
∴AE=,
∴DA=.
故答案为:.
14.
解:如图,以BC为边作等边△BCT,过点T作TH⊥AB于H,过点C作CK⊥AB于K,设CT交AB于点J.
∵∠ECD=∠BCT=60°,
∴∠ECB=∠DCT,
∵CE=CD,CB=CT,
∴△ECB≌△DCT(SAS),
∴BE=DT,
∴当点D与H重合时,DT的值最小,此时BE的值最小,最小值=TH的长,
∵CK⊥AB,
∴CK2=AC2-AK2=BC2-BK2,
∴52-AK2=72-(8-AK)2,
∴AK=,
∴AC=2AK,
∴∠ACK=30°,∠A=60°,CK=AK=,
∵∠BCJ=∠A=60°,∠CBJ=∠ABC,
∴△BCJ∽△BAC,
∴,
∴BJ,
∵BK=AB-AK=,
∴,
∴,
∴,
∵TH⊥AB,CK⊥AB,
∴TH∥CK,
∴,
∴,
∴TH=,
∴BE的最小值为.
15.##
解:如图,过点C作CE∥AD,交AB于E,
∴四边形AECD是平行四边形,
∴AE=CD.
由题意,得△EBC∽△PQR,
∴,即.
∴BE=3m.
∴AB=BE+AE=3+1.2=4.2(m).
即树高为4.2m.
故答案为:4.2.
16.
解:过点作轴于点,如图,
折叠,OA=2,AB=5,
,,
四边形是矩形,
,
,
,
,
设,则,
在中,
,
即,
解得,
,
,
轴,轴,
,
,
,
即,
解得,
,
.
故答案为:.
17.
解:设,
∵,
∴,,
∵四边形是平行四边形,
∴,,,
∴,,
∵平分,
∴,
∴,
∴,,
∴,
∵,
∴,
∴,
∴,
故答案为:.
18..
解:∵两三角形的相似比为,
∴它们的面积比为,
设较小三角形的面积为,则较大三角形的面积为,
则,
解得,
∴面积和为,
答:它们的面积和为.
19.
解:在和中,,
,
,
,
.
20..
解:∵ACDE,
∴△PBC∽△RBE,
∴,
∴BP=PR,
又∵△PCQ∽△RDQ,
∴,
∴QR=2PQ,
∴BP:PQ:QR=3:1:2.
21..
解:过点O作OMAB,交BC于点M,
四边形ABCD是平行四边形
,
.
22.(1);(2);(3).
解:(1)∵,,
∴;
(2)在△ADE中,
;
(3)∵,
∴,
∵,
∴,
∴,
∴.
